一道中考压轴题改编后的解法探究

2020-07-24曹路路

数理化解题研究 2020年20期

关键词：共圆位线辅助线

曹路路

(广东省广州大学附属中学 510000)

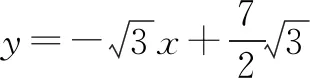
(1)如图1，求点A的坐标；

(2)如图2，连接AC，点P为△ACD内一点，连接AP、BP，BP与AC交于点G，且∠APB=60°，点E在线段AP上，点F在线段BP上，且BF=AE，连接AF、EF，若∠AFE=30°，求AF2+EF2的值；

(3)如图3，在(2)的条件下，当PE=AE时，求点P的坐标．

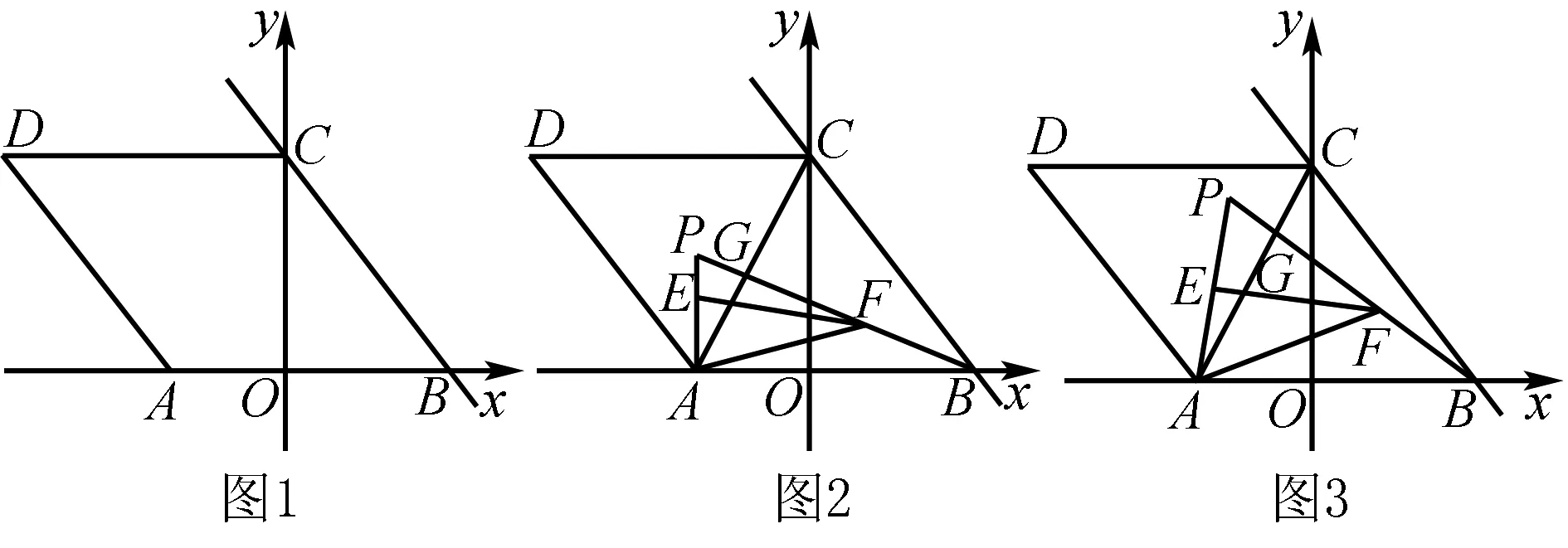
改编后(2019年广州市南沙区初三一模第25题)如图4，已知在平面直角坐标系中，点O为坐标原点，点A在x轴负半轴上，直线y=-x+6与x轴、y轴分别交于B、C两点，四边形ABCD为平行四边形，且AC=BC，点P为△ACD内一点，连接AP、BP且∠APB=90°．

(1)求证：∠PAC=∠PBC；

(2)如图5，点E在线段BP上，点F在线段AP上，且AF=BE，∠AEF=45°，求EF2+2AE2的值；

(3)在(2)的条件下，当PE=BE时，求点P的坐标．

第(2)问连接CE、CF、CA，结合已知条件和第(1)问的结论，易证△CEB≅△CFA，从而可得等腰Rt△CEF和Rt△AEC，所以EF2+2AE2=2CE2+2AE2=2AC2=144.

第(3)问标准解答：设AF=BE=PE=m，PF=n.在Rt△PEF中，EF2=m2+n2,

在Rt△PEA中，AE2=(m+n)2+m2.

∴(m2+n2)+2((m+n)2+m2)=144,

整理得2(m+n)2+3m2+n2=144①.

另在Rt△PBA中，PA2+PB2=AB2，整理得(m+n)2+4m2=144②.

由①②得：(m+n)2+n2-m2=0，∴n=0，即点P、F重合时恰有PE=BE.

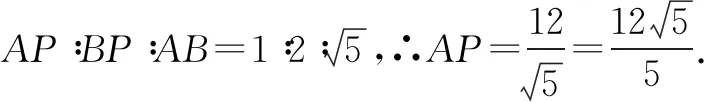
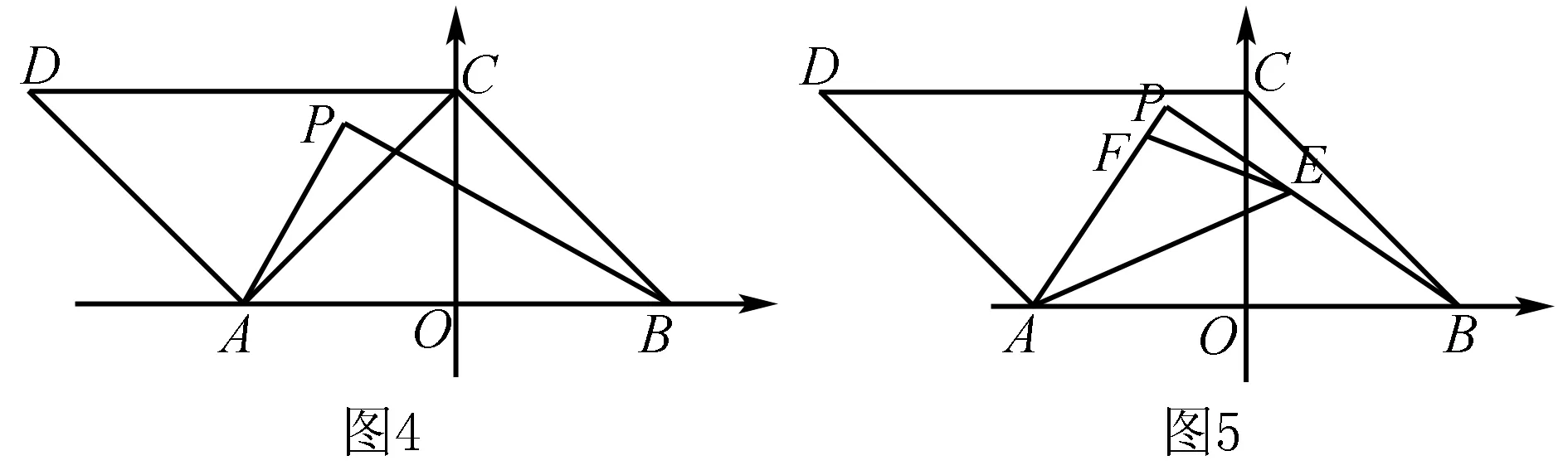
过P作PQ⊥AB于点Q，则△PAQ∽△BAP

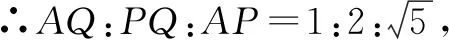
上述第(3)解答中最关键的是证明一个特殊情况，即当PE=BE时，点P与F重合.

下面针对此处给出另外三种证明方法：

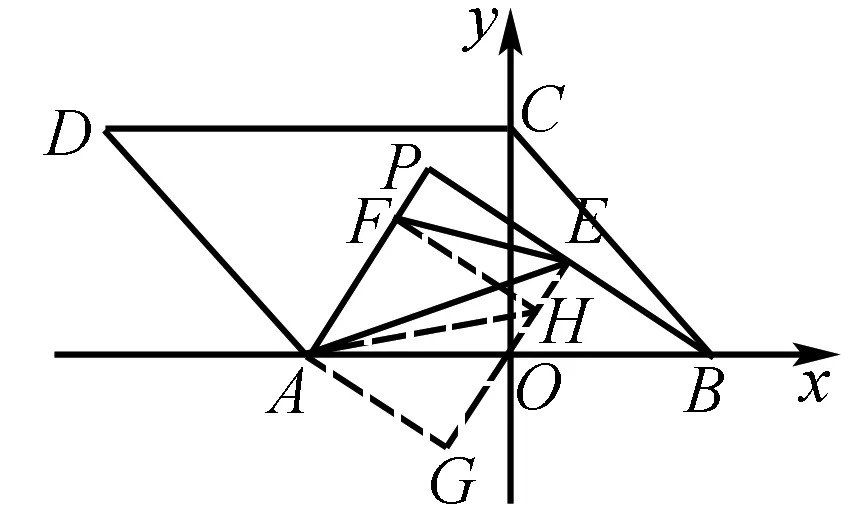
证法一连接OE并延长至点G，使得OE=OG，作FH⊥GE，连接AH，由OE是△ABP的中位线，可得OE⊥BP；根据△AOG≅△BOE，可得BE=AG=AF,∠G=∠BEO=90°，从而可得正方形AGHF，所以∠AHF=∠AEF=45°，从而AHEF四点共圆，又因为AGHF四点共圆，因此AGHEF五点共圆，显然只有当H与E重合时才能成立，从而F与P重合.

评析该证法从两个中点(点E和O)入手，巧妙运用三角形中位线和倍长中线法，然后运用四点共圆结合已知条件进行证明，对初中常见的辅助线作法进行了复习和巩固，也加强了对圆的学习，不失为一种好方法.

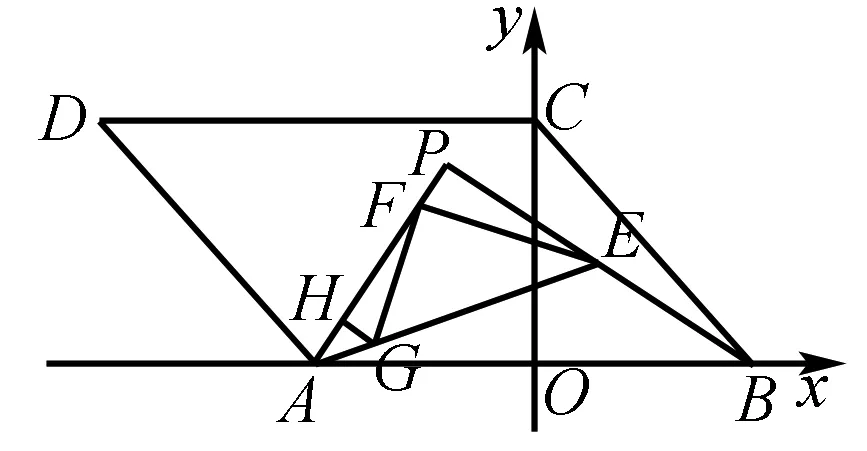
证法二作FG⊥EF，GH⊥PH，易得等腰Rt△GFE，所以FE=FG，从而△GHF≅△FPE，所以FH=PE=EB=FA，从而可得从而F与P重合.

评析该方法从45°角入手构造特殊的直角三角形，继而构造出最为常见的“一线三垂直”模型，从而达到要证明的目的，非常的巧妙.

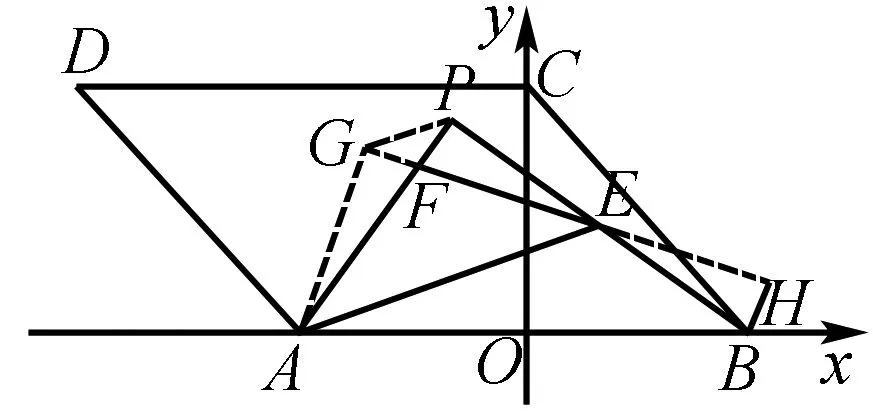
证法三分别过点A和点B作直线EF的垂线，垂足分别为G和H，连接PG.根据∠GAF=∠PEF=∠BEH,AF=BE，可得Rt△AGF≅Rt△EHB(AAS)，所以EH=AG.又因为△AGE为等腰直角三角形，所以AG=GE=EH.从而可得△GEP≅△HEB(SAS)，所以∠PGE=∠H=90°=∠AGF，所以A、G、P三点共线，从而可证F与P重合.

评析该方法从AF=BE入手，构造全等三角形，然后得出一个看似“奇怪”的结论：EG=EH，然后再次使用全等证明出F与P重合这一结论.