基坑边坡渗流稳定及可靠度研究

2020-07-24葛卉犇肖荣平

海河水利 2020年4期

葛卉犇，肖荣平，高颖，孙新

（江苏省淮阴水利建设有限公司，江苏淮安 223000）

1 引言

降雨、地震以及水位骤升骤降是引起边坡滑坡的3个主要因素[1]，滑坡造成的财产损害以及人员伤亡不计其数。降雨是最常见的自然现象之一，由降雨引起的滑坡事故占据很大比例，因此国内外专家学者都对降雨引起的滑坡灾害做了大量的研究。降雨入渗是一个复杂的过程，降雨引起土体内部孔压力变化属于饱和-非饱和渗流问题，孔压力变化对边坡滑坡稳定性有着重要的影响。同时，由于自然界中的土体受到自然环境以及人为因素的影响，大部分为非均质材料，使得使用传统的极限平衡法以及强度折减法等数值方法计算滑坡稳定性具有一定的局限性[2]。因此，使用不确定分析方法来评价滑坡的稳定性更加合理。李典庆[3]等提出了考虑土体参数空间变异性的边坡可靠度的非侵入式随机有限元法及其在实际工程中的应用。骆飞[4]等运用Bootstrap法对土体的参数摩擦角和黏聚力的随机取样数据重构，得到的结果更接近真实值。Li[5]等对均质及非均质土坡进行不确定性分析，研究了土体黏聚力与摩擦角的相关性，提出了考虑土体空间变异性的反应曲面分类方法。牛草原[6]等通过蒙特卡洛随机抽样法模拟开展了某均质边坡失效概率计算，探讨了3种因素对边坡失效概率的影响效应。

在众多可靠度分析方法中，蒙特卡洛随机抽样法由于条件限制少、计算结果易收敛以及实用性强等得到广泛应用[7-9]。因此，本文运用蒙特卡洛随机抽样法，以某一基坑边坡为工程背景，分析不同降雨工况下基坑边坡的渗透特性以及边坡滑坡的可靠度指标和失效概率，为相似的工程提供参考。

2 基本原理

2.1 非饱和土渗流及边坡稳定性理论

非饱和土渗流控制方程[10]如下：

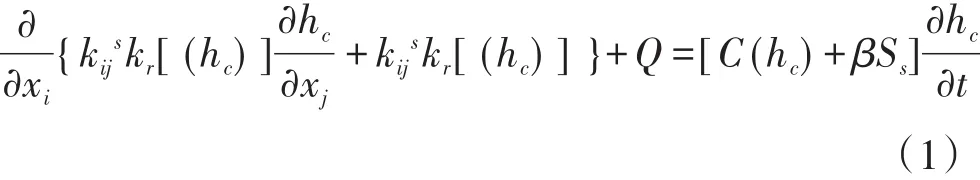
式中：xi，xj为i、j方向的位置坐标（m）；kijs为饱和渗透张量（m/s）；kr为相对透水率（m/s）；hc为压力水头（m）；β为非饱和常数；Ss为贮水量（m3）；Q为源汇项（m3）；C为比水容度；t为时间（s）。

非饱和土的抗剪强度理论采用Fredlund&Xing[11]提出的抗剪强度公式：

式中：s为非饱和土的抗剪强度（kPa）；c'为有效黏聚力（kPa）；σn为法向应力（kPa）；φ'为有效内摩擦角（°）；φb为土体基质角（°）；ua为破坏时破坏面上的孔隙气压力（kPa）；uw为破坏时破坏面上孔隙水压力（kPa）。

2.2 Monte-Carlo法基本原理

Monte-Carlo法又称为随机抽样技术或统计实验方法，其基本思路为：首先对影响边坡稳定可靠度的随机变量xi=(i=1,2,3,···,k)进行大量的随机抽样，然后把抽样值逐一代入功能函数式，建立边坡稳定性状态函数：

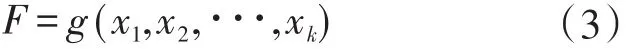
式中：F为稳定性系数，由式（1）可得到滑坡的稳定性系数Fi，如此重复N次，获得N个相对独立的稳定性系数样本值F1，F2，F3，···，FN。若定义Fi＜1为边坡滑坡事件，且在N次抽样中出现M次，则边坡失效概率为：

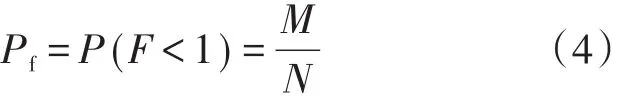
其均值和标准差为：

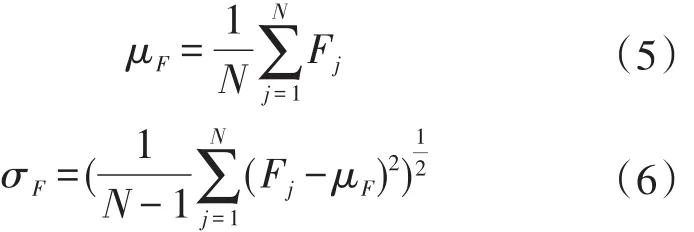
假设滑坡的临界稳定系数为μˉ，用β表示可靠度指标，则β可表示为：

岩土工程中假定平均稳定系数Fs=1时，边坡处于临界稳定状态，则β可表示为：

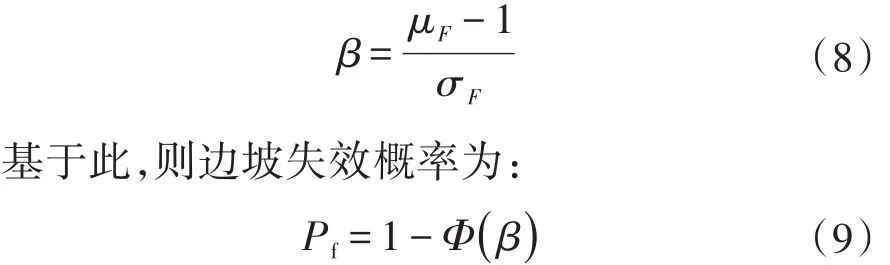
3 数值模型

某经济开发区有一基坑工程，其西侧紧邻河道，属古河道冲积地带，地下水较为丰富，而且由于基坑深度大于其东侧与建筑物距离，因此其被判定为一级基坑。基坑为两台阶边坡，边坡最大高度为8 m，上下台阶边坡中间设置操作平台，边坡计算几何模型如图1所示。边坡侧边设置有监测点，监测点从上到下编号。基坑土质较为复杂，上部主要是杂填土，土层根据边坡高度从上到下依次为素填土、粉质黏土和粉质砂土。网格单元类型主要为三角形及四面形，单元总体尺寸约为0.5 m。模型共剖分3 341个节点、3 216个单元，计算时间步长取6 h。

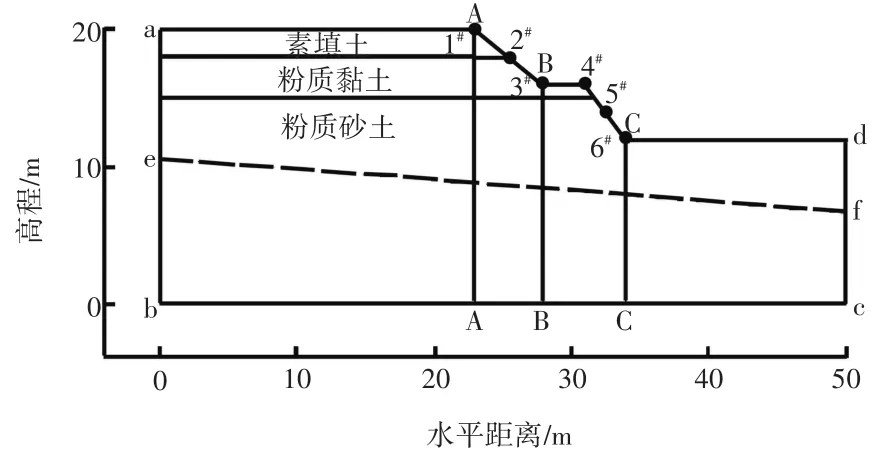
图1 基坑边坡计算几何模型

在进行降雨工况计算之前，需要计算边坡的初始渗流场。其具体边界条件如下：①ad为降雨入渗边界，当降雨强度小于土体渗透系数时，雨水全部渗入土体；②ae、df和bc为隔水边界；③eb、fc为水头边界，总水头分别为e、f的高程。

4 材料力学参数与工况

表1为基坑边坡各土层的物理力学参数。降雨入渗是饱和-非饱和渗流问题，采用Fredlund-Xing提出的土水特征曲线模型（SWCC）和非饱和土的渗透系数函数。

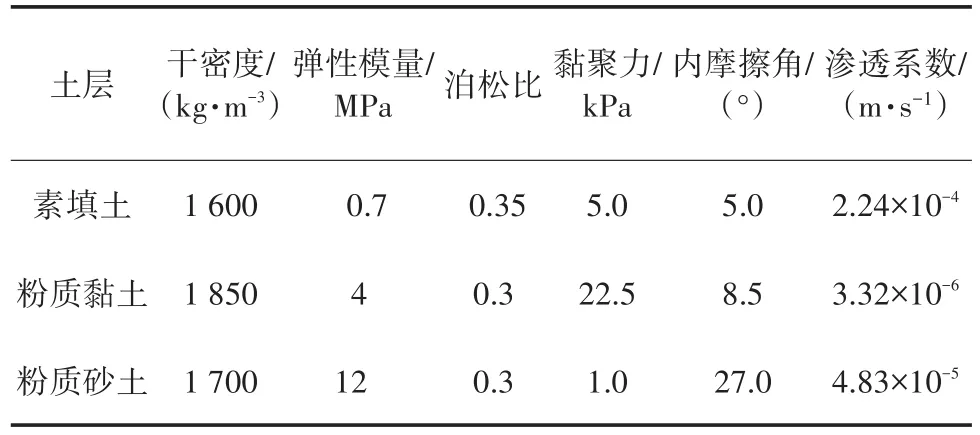
表1 基坑边坡各土层的物理力学参数

为研究不同降雨强度及不同历时对基坑边坡的渗透特性及稳定性影响，对基坑所在地区近50 a的降雨资料进行分析，拟定将大雨、暴雨以及大暴雨3种雨量作为本文的降雨工况，详见表2。

5 结果分析

5.1 孔压力分析

图2为不同降雨强度下基坑边坡不同监测点的孔隙水压力变化曲线图。从整体上来看，不管何种降雨强度，在降雨期间，各监测点的孔压力不断增大，监测点的高程越小，孔压力增大的幅度越小；降雨停止后，各监测点的孔压力不断减小，监测点的高程越小，最终的孔压力越大。对比降雨期以及停雨期边坡监测点的孔压力，可知监测点高程越大，降雨对其孔压力的影响较为明显。由于各监测点的位置不同，所以其初始孔压力也不尽相同，监测点高程越大，初始孔压力越小。对于同一水平面的监测点来说，在降雨期间靠近坡脚的监测点4比靠近坡顶的监测点3的孔压力随时间增大而增大的速度更慢，在停雨后监测点4的孔压力减小速率要比监测点3小。总的来说，在降雨量一定的情况下，降雨强度越大，边坡内部的孔压力变化越剧烈，而孔压力的急剧变化往往更容易引起滑坡事故。

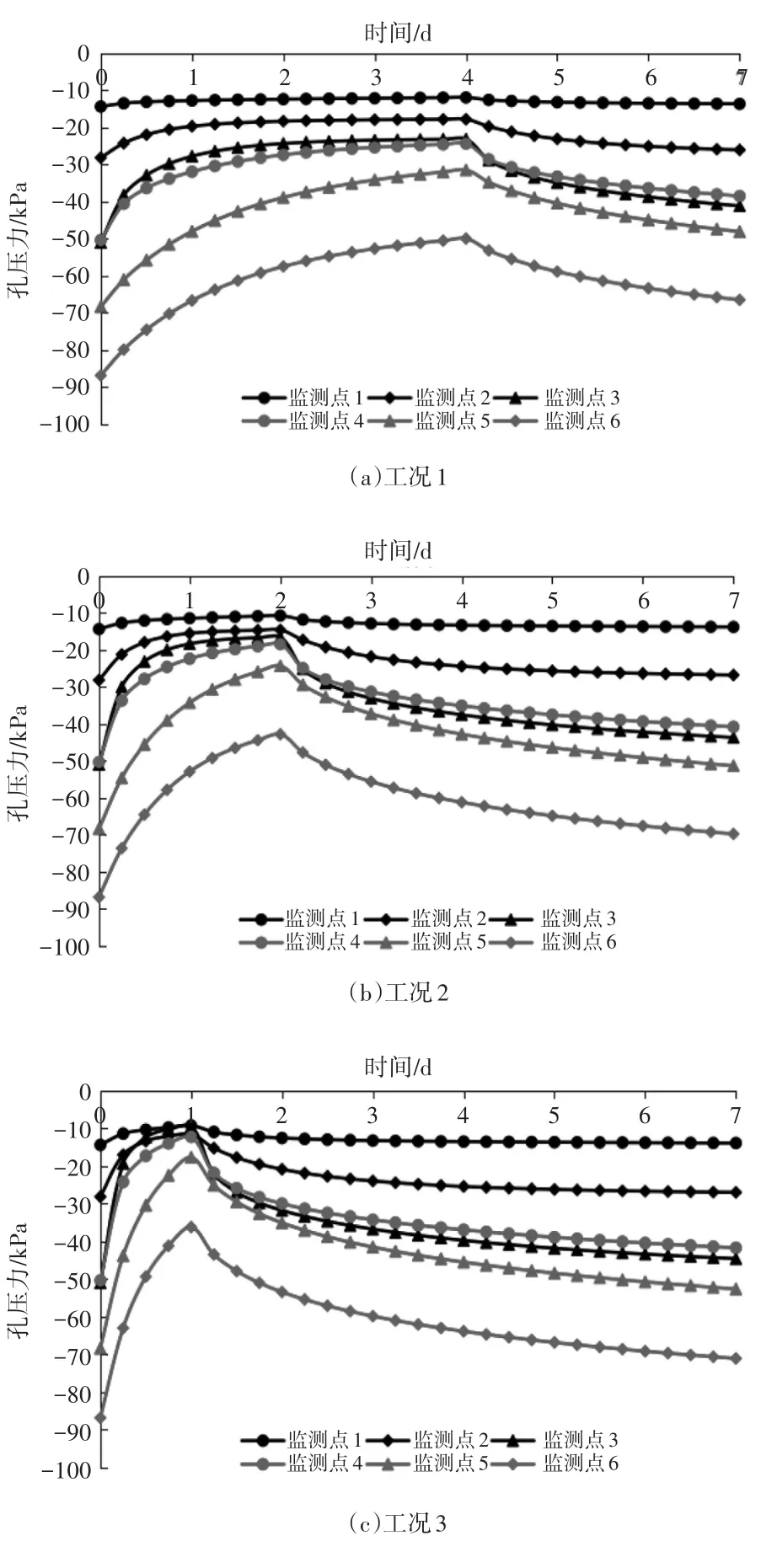
图2 监测点孔压力变化

5.2 安全可靠度分析

图3 为不同降雨强度下基坑边坡的安全系数随时间的变化规律图。由图3可知，降雨期间，随着雨水不断渗入土体，基坑边坡的安全系数不断减小；降雨停止后，边坡的安全系数逐渐增大。降雨强度越大，边坡的最小安全系数越小。大雨、暴雨和大暴雨工况下最小安全系数分别为1.043、1.038和1.034。为研究不同降雨强度工况下基坑边坡安全稳定性可靠度，在各个土层土体参数符合正态分布的条件下，对基坑边坡滑坡进行2 000次蒙特卡洛随机抽样法模拟，计算边坡在3种降雨强度工况下的可靠度指标和失效概率。由于文章篇幅有限，笔者仅取基坑边坡各个土层土体的一个物理参数黏聚力作为随机变量，该参数符合正态概率密度函数，其平均偏移为0、标准差为1 kPa、偏移值为±5 kPa。具体的正态概率密度函数，如图4所示。

图3 不同工况下基坑边坡安全稳定系数变化

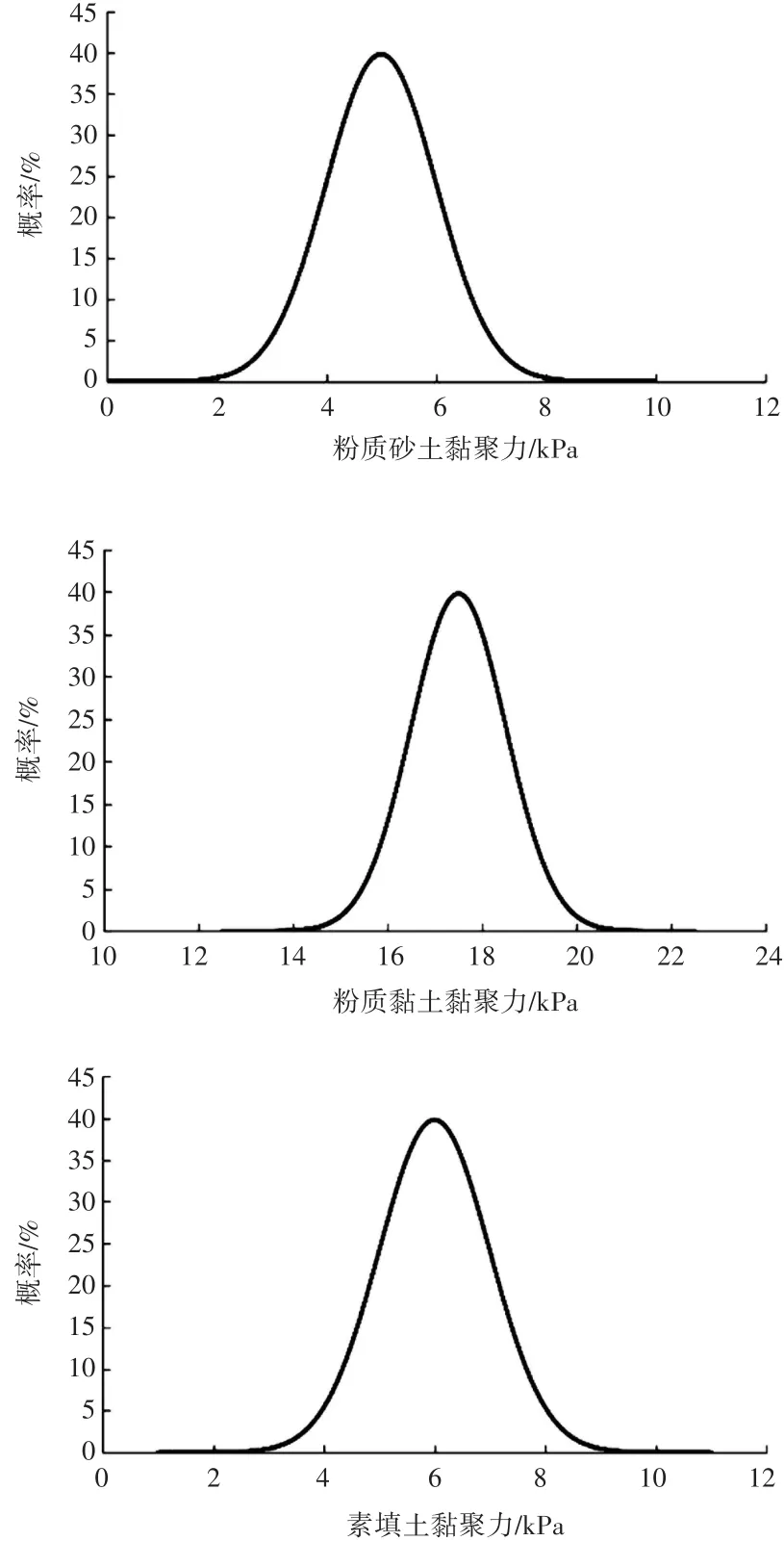
图4 基坑边坡各土层黏聚力的正态概率密度函数

由图5可知，在天然状况下，基坑边坡的平均稳定系数FS=1.072，标准偏差σF=0.043，可靠度指标β=1.673，失效概率Pf=4.25%；当对边坡施加大雨条件时，基坑边坡的平均稳定系数FS=1.043，标准偏差σF=0.042，可靠度指标β=1.027，失效概率Pf=14.60%；当对边坡施加暴雨条件时，基坑边坡的平均稳定系数FS=1.038，标准偏差σF=0.040，可靠度指标β=0.897，失效概率Pf=17.75%；当对边坡施加大暴雨条件时，基坑边坡的平均稳定系数FS=1.033，标准偏差σF=0.041，可靠度指标β=0.797，失效概率Pf=20.65%。

图5 不同降雨工况下边坡的安全系数

综上可知，随着降雨强度的增加，基坑边坡的稳定性逐渐减小，以天然工况下边坡的稳定系数为标准，3种降雨工况下稳定系数分别下降2.7%、3.2%和3.6%；边坡滑坡的概率也逐渐增大，以天然工况下边坡的稳定系数为标准，3种降雨工况下滑坡概率分别上升243%、317%和386%。这说明基坑边坡在降雨作用下，由于基坑各土层的渗透系数都大于最大降雨强度，降雨会全部渗入土体，但是由于降雨渗入深度不同，土层的孔隙水压力分布也不尽相同。降雨强度越大，土层的孔隙水压力在停雨时刻负孔隙水压力越大，基质吸力越小，使得边坡有效应力减小，降低了边坡的稳定性，使边坡的失稳概率不断增大。