土石坝渗流测压管水位预测方法研究

2020-07-24孙玉玲

海河水利 2020年4期

孙玉玲

（喀左县六官营子水利服务站，辽宁朝阳 122318）

1 引言

土石坝是一种广泛使用的坝型，在世界所有坝型中，土石坝的数量最多。众所周知，土石坝坝身不能过水，一旦坝身过水，土石坝将会类似于边坡一样，发生破坏，导致坝体失效。土石坝的两个重要关注点是渗流和稳定，坝体能否稳定决定是否可以有效挡水，而坝体渗流对土石坝的稳定具有重要影响，若测压管水位线过高，则土石坝的局部稳定性便无法保证[1]。所以，在土石坝的实际运行过程中，需要准确监测和预测坝体渗流水位线。测压管是一种有效的测量水头的仪器，在水位测量中有着广泛应用。对于土石坝而言，影响其渗流水位线的因素有水库上下游水位、天然降雨量及降雨历时等。对于降雨来说，不仅当下时段的降雨对渗流有影响，而且先前时间内的降雨也对渗流有影响。由于渗流的时间效应较长，所以对土石坝渗流水位线进行预测就显得比较重要。这就需要建立土石坝的渗流安全预测模型。在建立大坝安全预测模型时，常用的方法有统计模型、人工神经网络、支持向量机等，统计模型法中主要有多元线性回归、逐步回归、偏最小二乘回归等，其中逐步回归在回归方法中应用最多。杨杰、赵斌、吴云芳等[2-4]在研究大坝安全监测中，使用了人工神经网络的方法，对渗流、应力、变形等进行了分析，得到的预测结果和实际较为相符。岳建平[5]基于灰色动态神经网络建立了模型，用于预测坝体的其他指标，得到的结论较好。陈维江[6]在对回归模型的回归系数进行优化的过程中，引入了遗传算法，获得了较好的优化结果；苏怀智[7]为了提高预测模型的精度，将遗传算法和神经网络进行结合，但是模型的预测精度提高的幅度较小。张柯[8]在土石坝安全监测模型与安全性态模糊评价研究中，基于支持向量机法对土石坝的渗流安全等级进行了评价；李瑞光[9]基于主成分分析-支持向量机建立了土石坝渗流监测数据预测模型，得到的坝体监测数据分析预测结果基本满足要求。但是通过文献研究发现，人工神经网络应用于土石坝安全监测中，“过拟合”的现象较严重，导致在利用构建的模型进行预测时降低了预测的精度[10]。采用支持向量机法建立预测模型，需要对核函数和有关参数进行较为准确的估计，方能保证预测结果的精度。

为了建立土石坝的安全预测模型，笔者以某土石坝的渗流监测预测为分析对象，寻求构建预测模型的方法。以支持向量机方法为基础，引入单纯型粒子群优化算法，利用该算法对支持向量机的参数进行优化处理，对土石坝的测压管水位预测进行研究，从而得到建立的模型。利用该模型，以其他实测基本资料预测渗流水位，并与实测的测压管水位进行比较，判断该方法的精度和有效性；同时，与其他几种常见的预测模型进行对比，判断各方法的精度优劣。

2 预测方法

2.1 支持向量机

目前在很多领域都应用了支持向量机，依据支持向量机建立的模型，其学习性能和泛化能力的优劣受支持向量机的核函数和有关参数选择的影响[11]。核函数在支持向量机中非常重要，一些复杂的非线性问题可以通过合理的映射用高维空间中的线性问题予以表示，而对于这类线性问题的内积运算，可以采用核函数来实现[12]。对同一个问题，可以采用多种不同的核函数，但是需要寻找最优的核函数。常用的核函数有线性核函数、多项式核函数、径向基核函数、Sigmoid核函数，其中应用最多的是径向基核函数，也称为高斯核函数，其在任意分布样本中都可以应用，它的收敛域较大。基于此，支持向量机选择径向基核函数。在径向基核函数中，宽度参数σ、惩罚系数C、不敏感损失因子ε是3个重要的参数，其影响支持向量机的学习性能和泛化能力。在选择了径向基核函数后，支持向量机模型中需要优化的参数就是上述3个参数。

2.2 单纯型粒子群优化算法

单纯型法（SM）具有很好的局部搜索性，而粒子群优化算法（PSO）具有很好的全局搜索性，将两者结合起来，就构成了单纯型粒子群优化算法（SMP⁃SO）[13]。在寻找最优解的过程中，首先由粒子群优化算法提供一个全局位置，然后由单纯型法进行搜索，如果找到全局最优解，则结束寻优过程；若单纯型法未找到最优解，则在执行设定次数的迭代之后，也会将最优解的范围缩小，然后将该范围交给粒子群优化算法，组成新的微粒群，再进一步执行上述搜索步骤，直至获得全局最优解。

在支持向量机模型中，对径向基函数的3个参数进行优化时，引入单纯型粒子群优化算法，获得参数的最优解，以确保在样本数据训练和预测过程中，采用支持向量机可以得到较好的效果，因此该方法可以称为基于单纯型粒子群优化算法的支持向量机，简写为SMPSO-SVM。通过分析研究，提出了合理的流程，并结合算法内容，在Matlab中编写相应程序，实现了该方法的操作。

3 工程概况

某水库位于辽宁省某河流上，主坝为均质碾压土坝，大坝顶高程112 m，最大坝高34.1 m。水库总库容1.8亿m3，控制流域面积340 km2，含2座副坝，主要用于防洪和供水，兼顾发电，电站装机容量0.64万kW。水库目前已经运行近60 a，其间经过几次除险加固。

对该均质土坝进行渗流监测分析时，基于单纯型粒子群优化算法的支持向量机构建预测模型，训练样本选择2017年3月—2018年4月的实际监测数据，主要监测数据指标有测压管水位、水库水位、水库下游水位、降雨量，图1为水位的变化曲线。

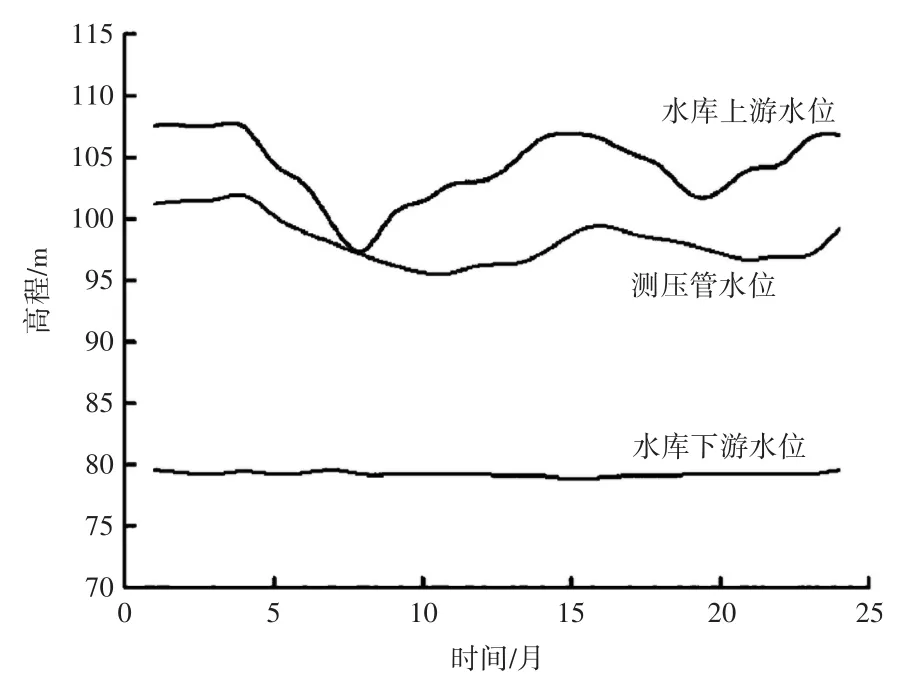
图1 水库上下游水位和测压管水位

3.1 影响因子和参数

土石坝测压管水位的影响因子主要是降雨量和时长、水库上游和下游水位。考虑这几个因子，建立测压管水位的抽象函数表达式：

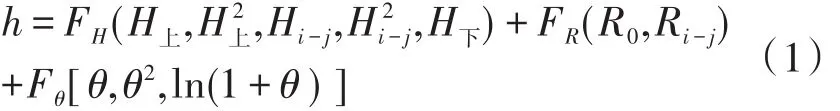
式中：h为监测当天采用测压管监测到的水位（m）；H上和H下分别为监测当天的水库上、下游水位（m）；Hi-j和Ri-j分别为监测当天之前第i～j天水库上游水位和降雨量的平均值；R0为监测当天的降雨量（mm）；θ为监测开始之日到正常观测的天数除以100（d）。

结合实际的监测资料，确定式（1）的影响因子也就是确定SMPSO-SVM预测模型的输入量，共包含 12个因子，分别为H上、H1-3、H4-8、H9-18、H19-38、H39-68、R0、R1-3、R4-8、R9-18、H下、θ。预测模型的输出量就是坝体的测压管水位。采用归一化方法对影响因子和监测值进行归一化处理，归一化公式如下：

式中：x'为参数归一化处理之后的值；x为参数的实际值；xmin为参数的最小值；xmax为参数的最大值。

在支持向量机模型中，参数C、ε、σ是3个需要优化的参数。在SMPSO中，设定的参数有微粒数和最大迭代次数，两者分别取为50和30，进而可以得到参数C1和C2值均为2，Vmax为0.001，w的初始值为0.95、最终值为0.2，减小的方式是线性减小。对SVM进行优化之后，得到参数C、ε、σ的值分别为183.67、0.024 2、0.979。

3.2 样本训练

训练过程中，所使用的数据是实际监测的50个样本，每个样本中包含12个影响因子的取值，样本数据详见表1。采用预测模型进行训练，整个过程在Matlab中实现，得到测压管水位的训练结果，并与实际监测结果对比，结果详见表2。训练结果与实际监测结果的对比曲线，如图2所示。

表1 50个训练样本m；mm；d

表2 测压管水位监测和训练结果

对比分析训练结果与实际监测结果可以发现，测压管水位的绝对误差均在0.5 m以内，误差较小，满足其他计算的要求。从图2可以发现，训练结果与监测结果的曲线非常接近，变化趋势一致，说明训练结果是有效的，基于单纯型粒子群优化算法的支持向量机建立的模型能够满足测压管水位的训练结果要求。

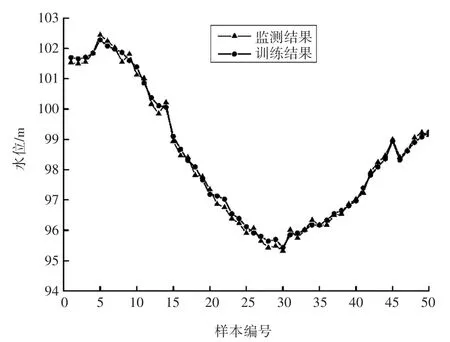
图2 训练结果与监测结果对比曲线

3.3 样本预测

为了对模型的预测效果进行评价，另外采用实际监测的10个样本作为预测样本，采用建立的SMPSO-SVM方法进行预测，预测结果和实际监测结果详见表3。预测结果与实际监测结果的对比曲线，如图3所示。

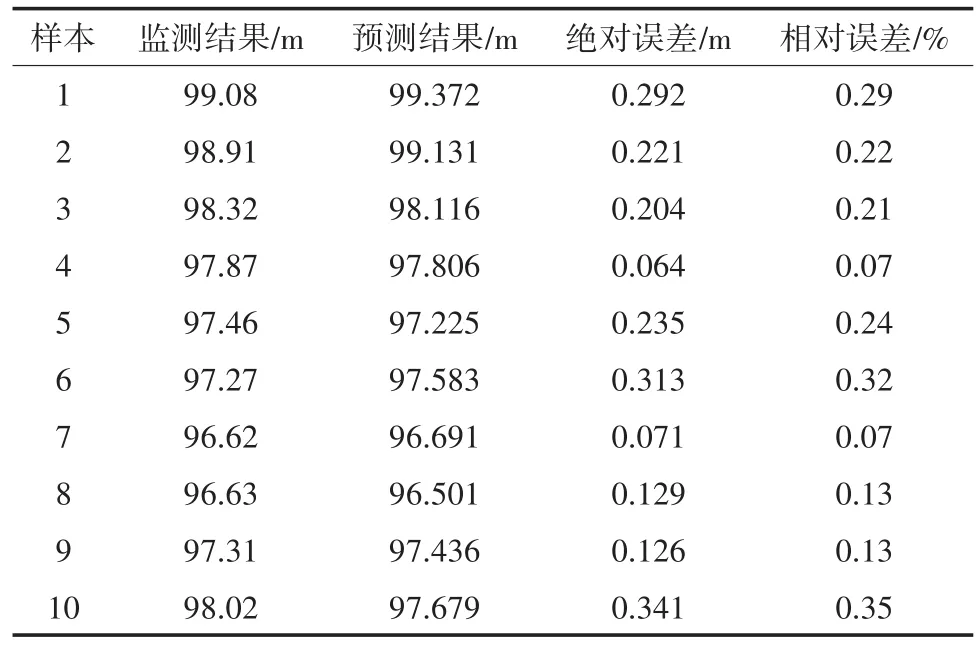
表3 测压管水位预测和监测结果

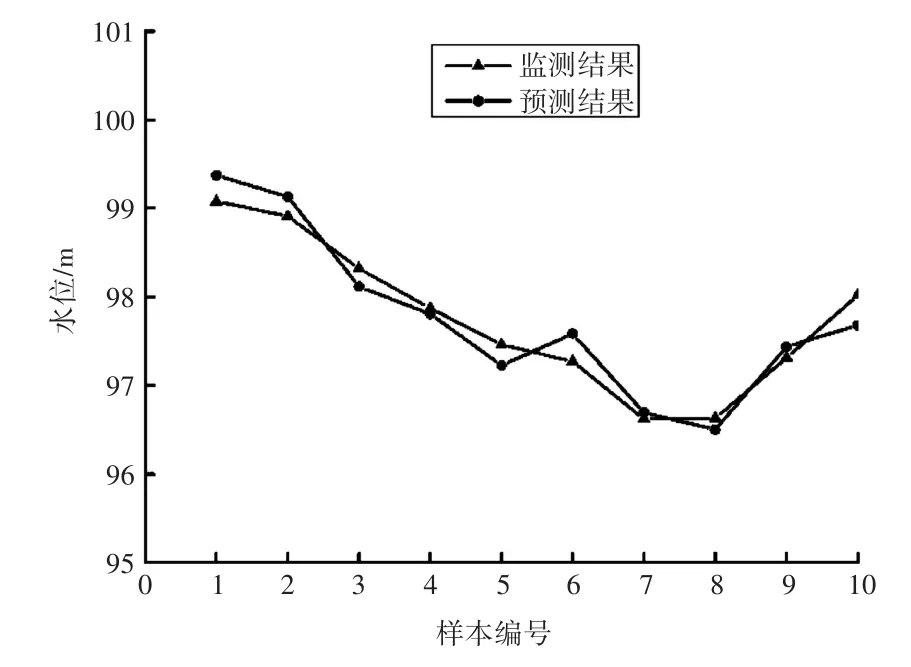
图3 预测结果与监测结果对比曲线

从表3可以看出，预测结果和实际监测结果的绝对误差在0.5 m内，最大相对误差为0.35%，绝对误差和相对误差均较小，若将水位预测结果应用于其他计算，如坝体渗流稳定分析等，该预测结果能够满足精度要求。从图3可以看出，预测结果与监测结果的曲线接近，两者的变化趋势一致，验证了SMPSO-SVM方法用于预测坝体测压管水位是满足要求的。

3.4 几种预测方法对比

为了进一步评价SMPSO-SVM方法的精度，选择了遗传回归、多元线性回归、最小二乘支持向量机、逐步回归模型，用这4种模型同时进行训练和预测。在应用这4个模型的过程中，影响因子的个数均为20个，以均方误差评价对比这些模型的精度优劣。表4给出了5个模型的训练和预测的均方误差。

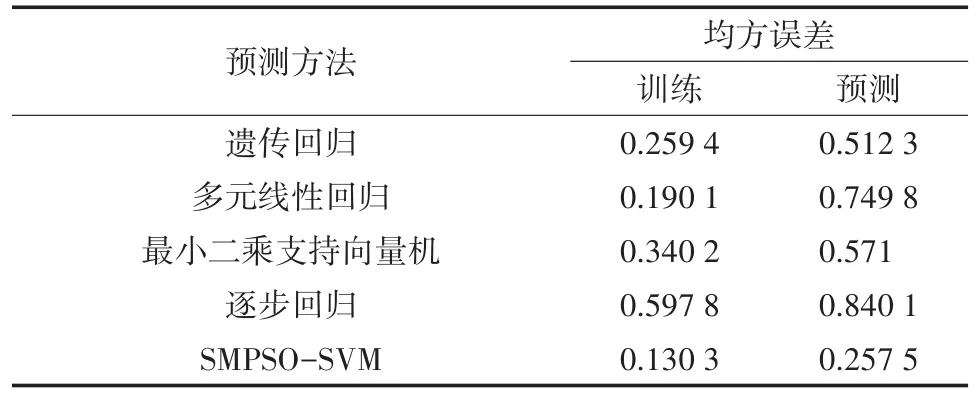
表4 几种方法预测结果

从表4可以发现，在训练过程中，均方误差最大的方法是逐步回归法，均方误差最小的方法是SMP⁃SO-SVM方法，SMPSO-SVM方法的均方误差显著小于其他4种方法训练的均方误差，这说明在训练过程中SMPSO-SVM方法的精度高于其他方法。在预测过程中，均方误差最大的方法是逐步回归法，均方误差最小的方法依然是SMPSO-SVM方法，而且SMPSO-SVM方法的均方误差显著小于其他方法。根据前文，在SMPSO-SVM模型中，影响因子有12个，不包含非线性的影响因子；其余4个模型的影响因子为20个，包含一些非线性的影响因子，因此可以得出SMPSO-SVM方法是一种只考虑线性影响因子且精度较高的模型。