星载氢原子钟用多段线圈式C场的仿真及应用*

潘志兵，谢勇辉，帅 涛，陈鹏飞，裴雨贤，潘晓燕，赵 阳，林传富

(1. 中国科学院上海天文台，上海 200030；2. 中国科学院大学，北京 100049)

星载氢原子钟利用基态氢原子的超精细能级跃迁信号进行计时，具有频率稳定度高、频率漂移率低等优点。目前,其长期频率稳定度可达3E-15/天，频率漂移率小于5E-15/天，并已在卫星导航定位系统如北斗系统和伽利略系统中得到了广泛应用[1-2]。

星载氢原子钟的发展方向是进一步压缩其重量和体积，并提高性能指标。频率稳定度理论计算公式[3-4]为

(1)

其中，α为氢原子钟的振荡参数，定义为

(2)

其中，QC为腔泡系统的Q值；η′为腔泡系统的微波填充因子，(1)式和(2)式中其他参数的意义详见文[3]。由(1)式和(2)式可知，星载氢原子钟的稳定度指标由腔泡系统的Q值、微波填充因子和原子驰豫时间等决定。为了保证星载氢原子钟的稳定度指标，要求腔泡系统具有尽可能高的Q值、微波填充因子和原子寿命。因此，腔泡系统的性能直接决定了整机性能指标，是星载氢原子钟的核心组件。

星载氢原子钟储存泡内的氢原子在轴向静磁场(C场)的作用下，由微波腔内的微波场激励氢原子自(F=1，mF=0)态跃迁至(F=0，mF=0)态。腔泡系统的微波填充因子η′反映了微波场与原子体系和轴向静磁场(C场)的耦合情况。C场的作用是将各量子态去简并，为原子跃迁提供量子化轴。如果C场在储存泡区域内的分布与微波场不一致，则处于该非均匀静磁场作用下的氢原子在储存泡内发生共振跃迁时，有部分原子的跃迁频率偏离期望的原子跃迁中心频率，从而降低了(0-0)跃迁的峰值强度[5-6]，进而影响跃迁谱线的增益和信噪比。所以，C场与微波场的耦合度是影响跃迁谱线质量的重要因素。

目前，本单位星载氢钟腔泡系统采用了电极式结构，其在储存泡区域内的微波场分布均匀，磁场强度波动小于1%[7]。因此,要求在储存泡区域内的C场也应当沿轴向尽可能均匀分布。考虑到星载氢原子钟的重量和体积，一般直接由直螺线管单层线圈，或者含有两端补偿的直螺线管双层线圈产生所需要的C场，但前者产生的磁场均匀度仍可以继续改善，后者增加了物理结构的设计难度，并且两端补偿线圈需要额外供电，也增加了电路部分的设计难度。

通过计算和仿真，设计了磁场均匀度更好的单层式单路供电的制造简单的多段线圈，并应用于星载氢钟腔泡系统，无需对星载氢原子钟电路部分[8]做任何改动。实验结果显示，可有效提升星载氢钟氢原子(0-0)跃迁的信号强度，并有助于提高频率稳定度。

1 直螺线管分析和仿真

直螺线管中心轴线上的磁感应强度[9]：

(3)

其中，μ0为真空磁导率；n为单位长度的匝数；I为通过直螺线管的电流；R为直螺线管半径；l1,l2分别为该点到直螺线管两端的距离。由(3)式可知，如果直螺线管的长度比半径大很多(l≫R)，则其中部磁感应强度约为B≈μ0nI，在靠近直螺线管的两端，磁感应强度将降低至B≈μ0nI/2。在直螺线管的中部区域，磁场总体上较为均匀，但两端的磁感应强度仅为中间区域的一半左右。考虑到星载氢原子钟实际应用时，原子储存泡顶端比较接近直螺线管的端面，必然导致原子储存泡区域内的C场不均匀。

按照星载氢钟当前使用的直螺线管实际尺寸，通过ANSYS电磁场仿真软件，可以对直螺线管在储存泡区域产生的静磁场进行仿真，仿真模型和结果如图1。

由图1仿真结果可知，储存泡内磁场强度最大值为6.71E-2 A/m，最小值和最大值差值为0.71E-2 A/m，两者相差达到10.58%。由此可见，实际工程上使用的普通直螺线管的磁场均匀度较为一般，有较大的提升空间。

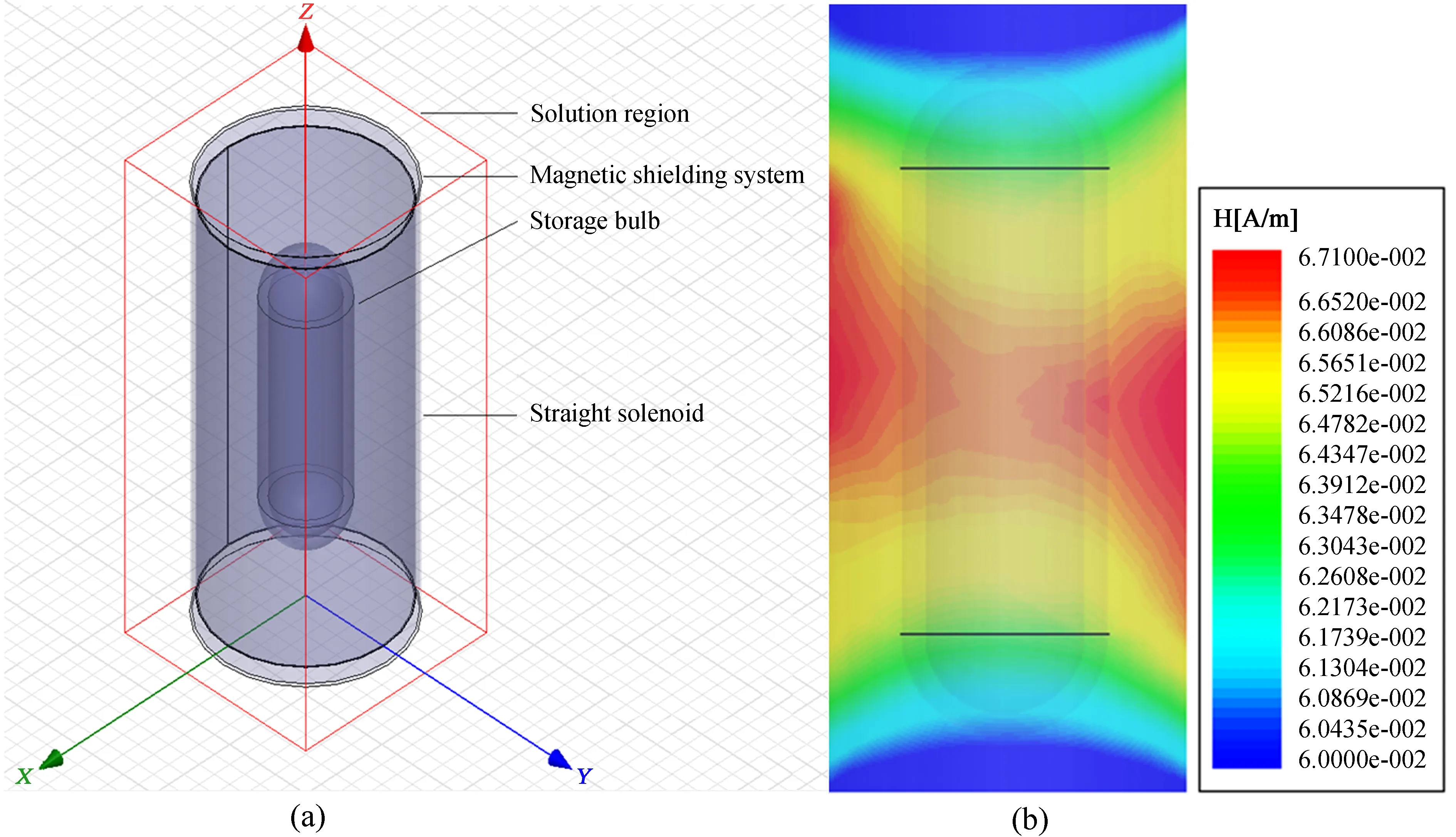
图1 (a) 直螺线管在储存泡区域的仿真模型；(b) 仿真结果Fig.1 (a) Simulation model of straight solenoid in the area of storage bulb; (b) Simulation results

2 九段线圈分析和仿真

2.1 多段线圈均匀度理论分析

亥姆霍兹线圈(Helmholtz Coil)是由两个相同的线圈同轴放置，其中心间距等于线圈的半径。如果这两个线圈通以相同电流，磁场会叠加增强，并在一定区域内形成均匀磁场[10]。亥姆霍兹两线圈相距为d且共轴，半径均为R，取两线圈圆心连线中点为x=0处，线圈中心轴线处磁场可表示为[11]

(4)

当d=R时，两线圈圆心之间的区域磁场较强且最均匀，两线圈圆心之外的区域磁场强度逐渐衰减[12]。

两段式亥姆霍兹线圈可在其中部区域产生均匀磁场。星载氢原子钟储存泡的轴向长度为150 mm，如果使用两段式亥姆霍兹线圈产生包含储存泡在内的较大区域的均匀磁场，则线圈半径约为150 mm，占用非常大的体积空间。考虑到星载氢原子钟的体积限制，故无法直接使用两段式亥姆霍兹线圈。

参考亥姆霍兹线圈的组合方式，可将多个较小的线圈进行特定的组合，以提高C场的均匀度[13]。多段线圈是将通以一路同大小、同方向电流的多个线圈同轴组合在一起。多段线圈由n个线圈组成，假设第n个线圈的中心坐标为Zn，长度为Ln，线圈匝数为Nn，则此线圈在C场中心轴线上产生的磁场可近似用直螺线管的公式计算：

(5)

因此，n个线圈组成的多段线圈在中心轴线上总的磁感应强度可表示为

(6)

多段线圈的各项参数，包含各段长度Ln、段数n、间距Zn+1-Zn、单位长度匝数Nn、内径R、总长度L均可以进行调整。综合考虑上述各个参数，并进行相应调整，即可设计出在整个储存泡区域的磁场均匀度很高的多段线圈。

2.2 九段线圈均匀度计算机仿真

(5)式和(6)式均为在C场中心轴线上场强的近似求解，并非精确的解析解，且未计算中心轴线外的整体区域的磁场。计算类似线圈结构中心轴线外的场强有很多方法[14-20]。但此处的多段线圈数量更多，结构更复杂，且要同时准确计算中心轴线上和中心轴线外的磁场强度，故采用有限元数值方法即电磁场软件仿真的方式进行整体全区域磁场的求解。

多段线圈可调节的参数很多，既要足够的可调节参数，又要降低计算机仿真和物理机械结构实现的复杂性。借助ANSYS电磁场仿真软件，主要开展段数为九段的多段线圈仿真工作。该模型综合考虑星载氢钟中与C场相关的其他结构，比如C场支架、储存泡和磁屏蔽系统等。线圈输入电流0.02 mA，刚好可以产生氢原子钟工作时所需要的约1mGauss磁场。经过对九段线圈的各个参数反复调整，获得了一组较优的线圈参数，仿真模型和结果如图2。

图2 (a) 九段线圈在储存泡区域的仿真模型；(b) 仿真结果Fig.2 (a) Simulation model of nine-section coil in the area of storage bulb; (b) Simulation results

由图2仿真结果可知，在九段线圈参数下，储存泡内磁场强度最大值为4.60E-2 A/m，最小值和最大值差值为0.04E-2 A/m，两者相差0.87%，磁场均匀度比直螺线管有了较大的提升。

直螺线管和九段线圈在储存泡区域中心轴线上产生的磁场均匀度如图3。由图3可知，直螺线管在储存泡区域中心轴线上产生的磁场均匀度在91%左右，但九段线圈在储存泡区域中心轴线上产生的磁场均匀度可提升至99.2%。

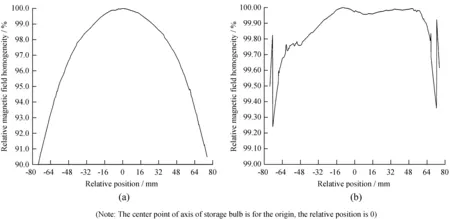
图3 (a) 直螺线管在储存泡区域中心轴线上的磁场均匀度；(b) 九段线圈在储存泡区域中心轴线上的磁场均匀度

计算和仿真表明，多段线圈的段数越多，可调节的参数也越多，更容易实现原子储存泡区域内极佳的磁场均匀度。各类线圈在储存泡区域的磁场均匀度见表1，由表1可知，九段线圈可以在整个储存泡区域实现大于99%的磁场均匀度。

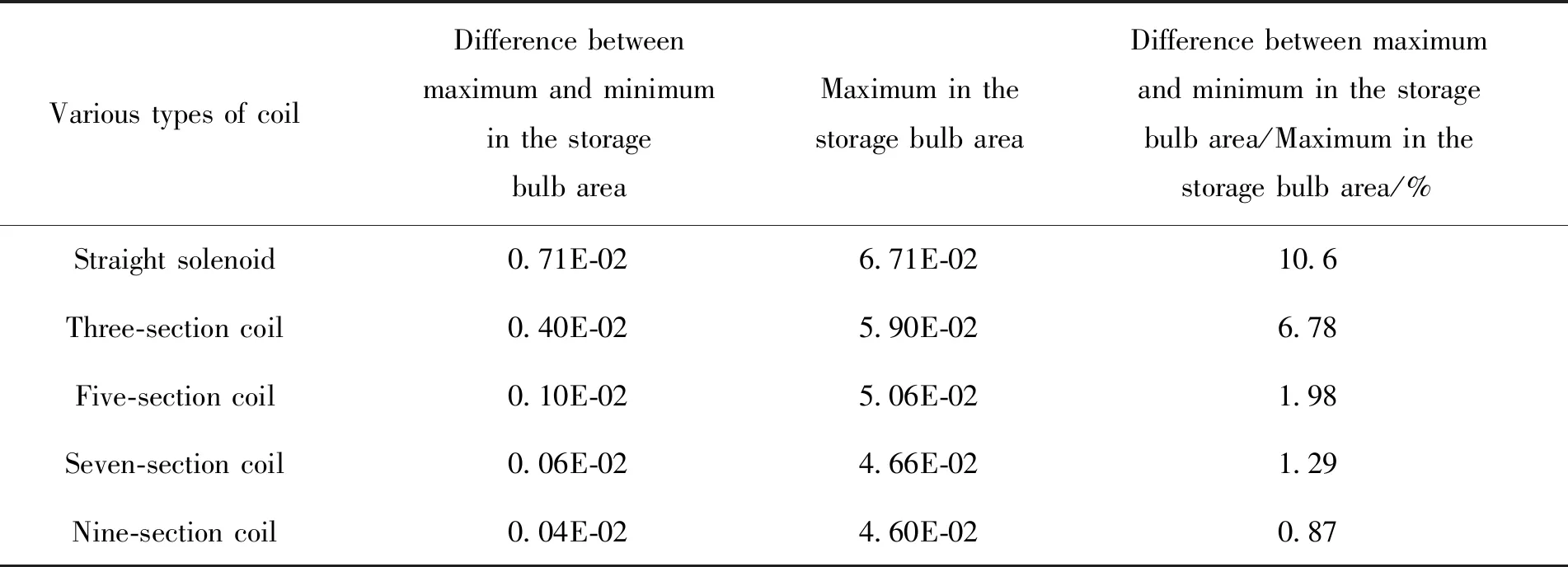
表1 各类线圈在储存泡区域的磁场均匀度分布情况Table 1 The homogeneity of magnetic field of various types of coil in the storage bulb area

3 原子跃迁信号对比

按照仿真软件给出的较优的九段线圈设计参数，绕制了实际的C场线圈并应用于星载氢原子钟，如图4。在保持其他实验条件不变的情况下，实际测量了九段线圈作用下的氢原子(0-0)跃迁的信号幅度，并与直螺线管进行对比，从而判断磁场均匀度对信号的提升作用。

图4 九段线圈实物图

在实验过程中，磁屏蔽系统已使用大电流退磁，处于已退磁状态。谐振腔的微波输入功率为-90 dBm，微波腔谐振频率调节至原子跃迁频率附近，1 420.405 751 MHz ± 5 KHz，两个线圈产生的C场大小均约为1mGauss。直螺线管线圈作用下的氢原子(0-0)跃迁信号增益为2.975 1 dB，九段线圈作用下的氢原子(0-0)跃迁信号增益为3.290 1 dB，九段线圈信号增益较直螺线管增加0.315 0 dB，提升效果明显，两者对比如图5。

图5 (a) 直螺线管作为C场时的氢原子(0-0)跃迁信号增益；(b) 九段线圈作为C场时的氢原子(0-0)跃迁信号增益

4 频率稳定度性能对比

完成直螺线管和九段线圈各自作为C场的原子跃迁信号幅度测试对比后，联合电路部分进行了闭环测试。保持其他参量不变，将C场线圈作为唯一可变参量，测试两者对星载氢钟频率稳定度性能指标的影响。

每次频率稳定度测试时间均为72 h，阿伦方差测试对比见表2和图6。从表2和图6可以看出，在1～1 000 s短稳时，应用九段线圈后的星载氢原子钟具有更好的频率稳定度，且在10～1 000 s表现更为明显。在10 000 s长稳时，九段线圈的性能稍好，由于极易受到温度波动和频率漂移(Freq Drift/Day≈1E-14)等众多因素的影响，以及实验测量环境的限制，暂未得出九段线圈性能明显更优的数据。

表2 直螺线管和九段线圈作为C场时的阿伦方差对比测试Table 2 The comparison of Allan deviation between straight solenoid and nine-section coil using for C field

图6 直螺线管和九段线圈作为C场时的阿伦方差对比测试Fig.6 The comparison of Allan deviation between straight solenoid and nine-section coil using for C field

5 结 论

腔泡系统是星载氢原子钟的核心组件，其微波填充因子η′反映了微波场与原子体系和C场的耦合度。电极式腔泡系统储存泡区域内的微波场分布均匀，磁场强度波动小于1%，因此，C场均匀度是影响氢原子(0-0)跃迁谱线性能的重要因素。软件仿真表明，直螺线管的磁场非均匀度约为10%。而九段线圈可以实现小于1%的磁场非均匀度。实际工程应用表明，按照仿真设计优化参数绕制的九段线圈，可以有效提升星载氢原子钟腔泡系统的原子跃迁信号。整机性能阿伦方差频率对比表明，配置九段线圈的星载氢原子钟中短期稳定度性能表现更优。九段线圈在星载氢原子钟腔泡系统上的应用，可以在不增加机械结构和电路设计复杂度的同时，提升星载氢原子钟腔泡系统的性能和整机稳定度，并已得到成功验证和应用。未来将对多段线圈长度段数和间距等参数继续探索，寻找静磁场-微波场耦合度更优越的腔泡系统配置方案。