比值校正法在射电频谱中的应用*
2020-07-24张燕坤李明悦何乐生
张燕坤,董 亮,李明悦,何乐生,汪 敏
(1. 中国科学院云南天文台,云南 昆明 650216;2. 中国科学院大学,北京 100049;3. 云南大学信息学院,云南 昆明 650504)
谱线在研究天体的物理或化学环境、演化历程以及天体分类等方面具有重要作用,是天文学研究的一个工具。与各种辐射机制预言的功率谱相似,谱线研究涉及一个频率、多个频率或者连续谱,可以是吸收线,也可以是发射线。它们来自于不同层级的天体,比如恒星、星云、星系、本星系群或者整个宇宙。通过多波段观测可以对这些天体形成一个系统的认识。在众多的谱线中,HI21 cm谱线是验证大爆炸理论、揭示宇宙早期再电离阶段的重要探针[1];光谱学中的各类线系、复合线可以用来研究天体的温度、速度等物理量;尘埃辐射和分子谱线是研究恒星形成、星际介质的重要工具。
各类谱线具有不同的波长,其中很多在射电波段(0.3 mm~20 m),可以通过射电望远镜或天线阵列对它们进行探测。为了尽可能探测到较多的谱线,除了需要好的射电天文观测环境外,还要望远镜的灵敏度和分辨率足够高。因此,低噪声放大器、宽带接收机、大口径天线、多波束或焦面阵(大视场)等关键设备的研发成为当前的重大课题。同样,多通道数字终端、高速数据处理和存储设备研发,甚至观测技术或方案等也很重要。
除了空间分辨率以及时间分辨率的要求,分子天体物理和谱线观测对终端设备的频率分辨率也提出了很高的要求[2]。在星际介质和恒星形成的研究工作中,天体的运动速度或速度梯度场是很重要的物理量。它在天体测量学、星系动力学中定义的本地静止标准中表现为红移或蓝移,即多普勒运动。这个速度会使探测到的谱线频率相对于实验室测得的频率有一定漂移,如图1,从H(96)β的离散谱形能够得到天体的速度、温度等物理信息,表明频谱分辨率越高,越能反映真实的天体物理信息。

图1 天马65 m望远镜观测到的H(96)β频谱。图像上沿坐标轴显示的是经过多普勒修正后的频率
实际上,观测设备和观测方法会在频谱上造成一定的频率漂移和速度展宽,从而引入系统误差,因此还需要频谱校正。尽管该技术在工程领域得到广泛应用,但是天文领域的应用仍然欠缺。在频谱分析时,一般采用拟合方法检验通道稳定性和通道间隔一致性,很少用到频谱校正的方法,也没有校正偏移量。这对于频率分辨率要求不高(δ≈10~102Hz)的谱线观测是合适的,但是,随着天文观测要求的提高,终端精度和稳定性也相应提高,此时简单的拟合不再适应,频谱校正就显得尤为重要。
频谱校正是信号处理领域重要的研究课题。由于计算机只能对有限个样本和采样点进行计算,因此,需要对时域信号进行截断和数字离散化,这不可避免地造成了能量泄漏和栅栏效应,使得离散频谱的幅值、相位和频率产生较大的误差[3-4]。在对单频率谐波信号加窗处理后,幅值误差最高可达36.4%,相位误差可达 ± 90°,频率误差可达 ± 0.5倍频率分辨率[5]。
目前,离散频谱校正的方法有很多,其中比值校正法较为常用。根据原时域信号组成结构的不同,主要分为两类:一类频谱校正方法主要针对单频信号,另一类针对密集频谱。由于射电天文的谱线信号主要是单频信号,即使是能级分裂造成的各点频信号间隔也较大,因此,本文只讨论单频信号的频谱校正。对于单频信号,国内外有5种对功率谱校正的方法:比值校正法、能量重心校正法、全局快速傅里叶变换及局部连续细化傅里叶分析法、相位差法、相位差法 + 单点傅里叶变换法[6]。本文的实验模拟了射电天文观测软硬件系统,并采用算法简单、运算速度快、精度较高的比值校正法[7],对经过LabView程序、捷变收发器的噪声源信号进行频率定标。
1 比值校正法
在谱线研究中,频率、流量和偏振是重要的观测量。由于频率稳定性和测量偏差在积分观测中会间接影响流量乃至偏振的测量与定标,因此,仅介绍比值校正法在频率定标方面的应用。
利用频率归一化后差值为1的主瓣峰顶附近两条谱线的窗谱函数比值,建立一个以归一化校正频率为变量的方程,解出归一化校正频率,进而进行频率、幅值和相位校正的方法称为比值校正法[8]。解归一化校正频率的方法有多种,直接导出公式的方法称为比值公式法,利用迭代求解的方法称为比值迭代公式法,用搜索求解的方法称为比值峰搜索法。
假设归一化窗函数的频谱模函数表达式为W1(f1),由于主瓣内幅值为正,此时频谱模函数与归一化窗谱函数完全相等,W1(f1)与y轴对称,即主瓣中心是坐标原点。
如果周期信号的频率恰好对正某一发射(吸收)谱线频率,那么计算得到的频率、幅值和相位都是准确的。更一般的情况是,信号频率没落在通道中心位置,因此,峰值谱反映的频率和幅值都不准确,相位误差也较大。主瓣中心并不在坐标原点,而是有一定偏移▽f1(-0.5 ≤▽f1≤ 0.5)。在射电天文的高精度实测中,需要精确测量得到谱线的频谱信息,因而频谱的偏移要尽可能消除。
设fy表示谱线发射频率,fr表示频谱仪接收的频率,在设备良好的情况下,地面测试实验得到的结果应是fy=fr。由于谱线发射频率fy处在特定通道K(幅值谱谱线号)内,但不一定处在该通道的中心位置f0处,因此fy≠f0。加上时域信号被截断的影响,fy与f0之间的偏差较大。经过频谱校正,可以在较高精度(Hz级)下使得f0_c=fy=fr。
实际频谱中,假设采样点数为2N,采样频率为2fs,那么通道数为N,采样带宽为fs,且K∈[1,N/2-1][9]。若通道K的幅值为Yk,其两侧K-1,K+ 1通道的幅值分别为Yk-1,Yk+1,那么K通道对应的频率为
(1)


图2 Yk-1> Yk+1时对应的离散信号示意图Fig.2 Schematic diagram of discrete signal corresponding to Yk-1> Yk+1
(2)


图3 Yk-1< Yk+1时对应的离散信号示意图Fig.3 Schematic diagram of discrete signal corresponding to Yk-1< Yk+1
(3)
对于矩形窗而言,其频率校正量为
(4)

(5)
如图4,以上校正算法适用于起始频率为0 Hz的离散频谱,但实际应用中,起始频率一般不为0 Hz,因此,还需要针对特定领域进一步计算。在射电频谱中,真实的频率为
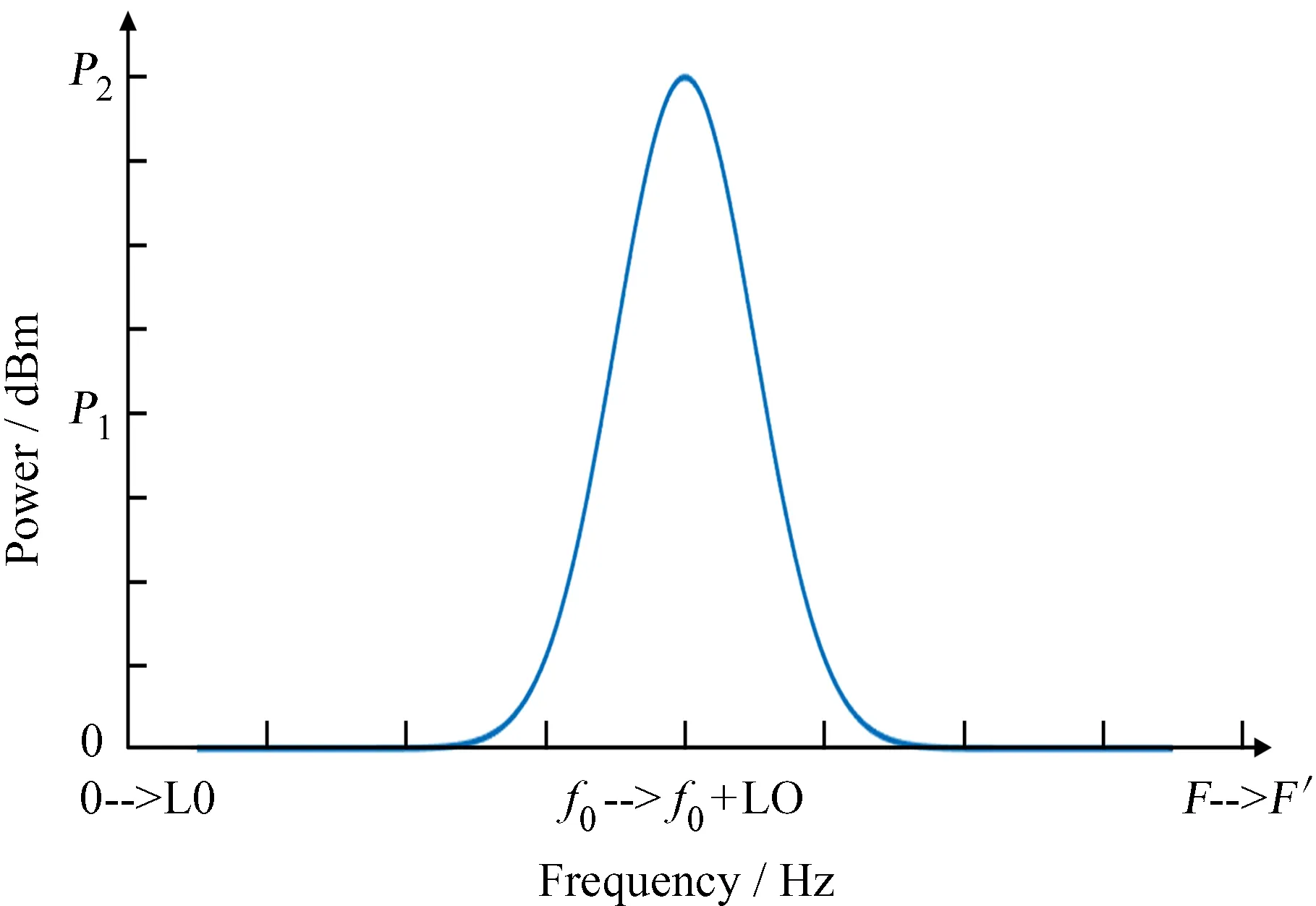
图4 考虑本地振荡频率后的校正示意图
fr=fLO+f0_c,
(6)
其中,fLO为本地振荡器的频率。若有多级本振,还应把各级本振频率求和,才能得到fLO。
2 实验设置
射电天文观测中,天文谱线信号在L波段及其以上频率(>1 GHz),因此需要降频,以降低数字后端采样的压力。观测源的信号经过天线、接收机后,其频率被调制到几十到几千兆赫兹,随后将中频信号送至终端进行采样和校准。
为了模拟这样的一个中频信号,采用标准信号源并设置输出频率为f0=141 800 000.00 Hz。同时,使用捷变收发器NI2901作为模数转换和数据采样设备,并编写LabView程序设置终端参数并控制运行过程。另外,通过程序中的功率谱计算,在输入带宽内划分出N个数字通道,从而将一定的信号带宽细化,这样就能提高频率分辨率,满足对频谱分辨率的不同需求。
实验设置了不同的频率分辨率,以观察比值校正法在不同需求下的表现。虽然分辨率越高对天文观测越有利,但是需要与当前技术发展水平相适应,因此参数配置要合理,具体情况见表1。从表1中载波输入和实际载波部分可以看出,设定的参数与设备响应间有一定的差值,这给数据分析带来不便。同时,为了使实验具有统计意义,对每组设置分别测试5次。

表1 不同频率分辨率下的参数设置Table 1 Parameter Settings at different frequency resolutions
对于特定观测波段,由于观测源和探测的分子不同,输出的中频信号也不同。考虑到40 m射电望远镜分子谱线终端的中频输入带宽是1 GHz(升级改造后为2 GHz),谱线信号可能出现在带通几十或几百MHz的位置,因此还设置了80.0 MHz和270.8 MHz的实验组,来研究比值校正法在不同输出信号、不同频率分辨率下的表现。与表1参数不同,当射频信号为80 MHz时,载波输入为79.979 5 MHz,实际载波为79.979 5 MHz;当射频信号为270.8 MHz时,载波输入为270.769 5 MHz,实际载波为270.77 MHz。
3 结果分析
通过多次测试和数据分析,发现和解决了理论和技术上的缺陷,并有了一些结果。认真分析这些结果,有助于进一步研究频谱校正理论,并把相关方法应用到实际观测中。本文针对不同目的设置了不同的实验组。
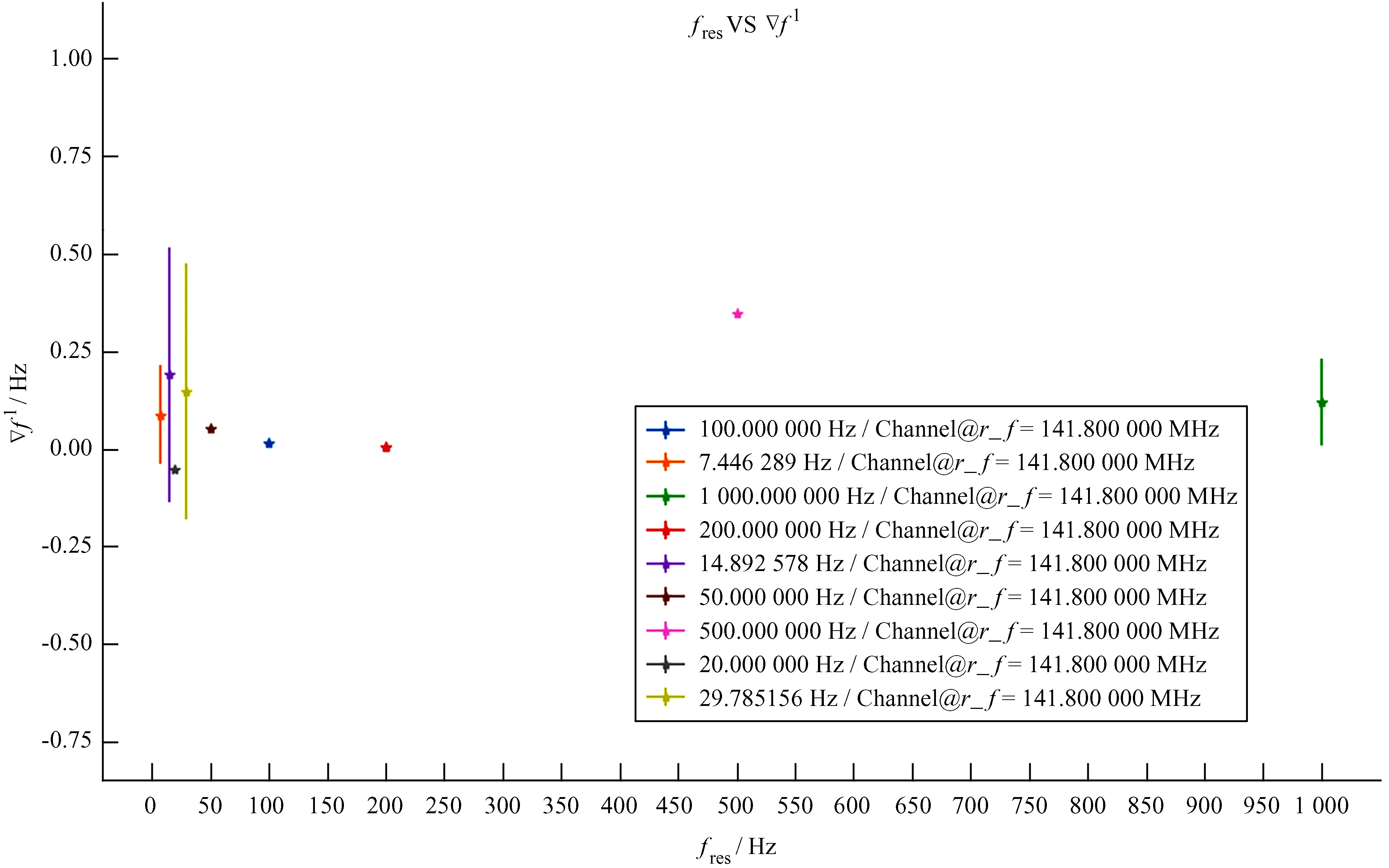
首先,归一化频率偏移量▽f1在射频信号相同、频率分辨率不同的情况下表现出一定的规律。在表2和图5中,0~4分别表示5次测试的序号。从图5可以看出,当频率分辨率较高时,各次测试的值不尽相同,而在频率分辨率较低时各次测试一致性较好,这说明系统在较高频谱分辨率下不稳定,并且▽f1大于0的散点较多,即多数情况是Yk-1 表2 射频为141.8 MHz、频率分辨率不同时的多次测试结果Table 2 Results with radio frequency of 141.8 MHz and different frequency resolution 图5 射频为141.8 MHz、频率分辨率不同时的多次测试结果Fig.5 Multiple test results with radio frequency of 141.8 MHz and different frequency resolution 表3 射频为141.8 MHz、频率分辨率不同时▽f1的均值与标准差 其次,频率分辨率相同,射频信号不同,归一化频率偏移量▽f1也不同。从表4和图7可以看出,射频信号分别为80 MHz,141.8 MHz和270 MHz时,归一化频率偏移量有较大差别,并且频率分辨率较高和较低时有很大不同。从图7可以看出,当频率分辨率为50 Hz/channel或200 Hz/channel时,3个信号的归一化频率偏移量▽f1∈[-0.2, 0.2]。结合图5、图6,可知此时系统最稳定。 图6 射频为141.8 MHz、频率分辨率不同时的分析结果Fig.6 Analysis results of radio frequency about 141.8 MHz with different frequency resolutions 表4 ▽f1在不同射频、不同频率分辨率情况下的值Table 4 The value of ▽f1 with different radio frequency and frequency resolution 图7 不同射频信号、不同频率分辨率下的归一化频率偏移量Fig.7 Normalized frequency offsets at different radio signals and different frequency resolutions 以上结果可以这样理解:由于比值校正法只使用了3个临近点,因此,对频率分辨率显示出很高的依赖性。如果在高频率分辨率情况下观测,再分析归一化频率偏移量,那么比值校正法是最好、最快的校正方法。 比值校正法简单、实用,这给射电天文频谱分析带来了很大的便利。本文基于测试频点已知的情况展开研究,虽然与实际观测有一定差距,但是对于未来观测数据质量的提升是一项具有开拓性的工作。尽量减小系统误差,并避免外界干扰,这样天体的动力学或运动学条件、温度和密度等研究成果才有较高的置信度。该研究的具体意义有3点:(1)检验信号源或者本振的频率稳定性,长期监测可以得出它的变化规律;(2)频率切换观测时,需要不断改变本振频率,因此,需要监测本振的频率稳定性和准确性;(3)实际天文观测中,一般不需要对频率稳定性定期检测,但是该工作对确定仪器误差、检测仪器性能以及对更深入的频率定标和监测都有参考价值。 在未来,利用40 m射电望远镜探测频线信号前,本文解决了频谱校正的问题,同时也指明了实测时的分辨率设置(50 Hz/channel或200 Hz/channel),给动态校正频谱的工作提供了参考。另外,天体的多普勒效应也给频谱带来了频率漂移,这将是下一步研究的内容,可以和选择观测源和谱线等工作一起进行。 致谢:衷心感谢杨志坚教授在编程和测试过程中给予理论指导并提供无私帮助。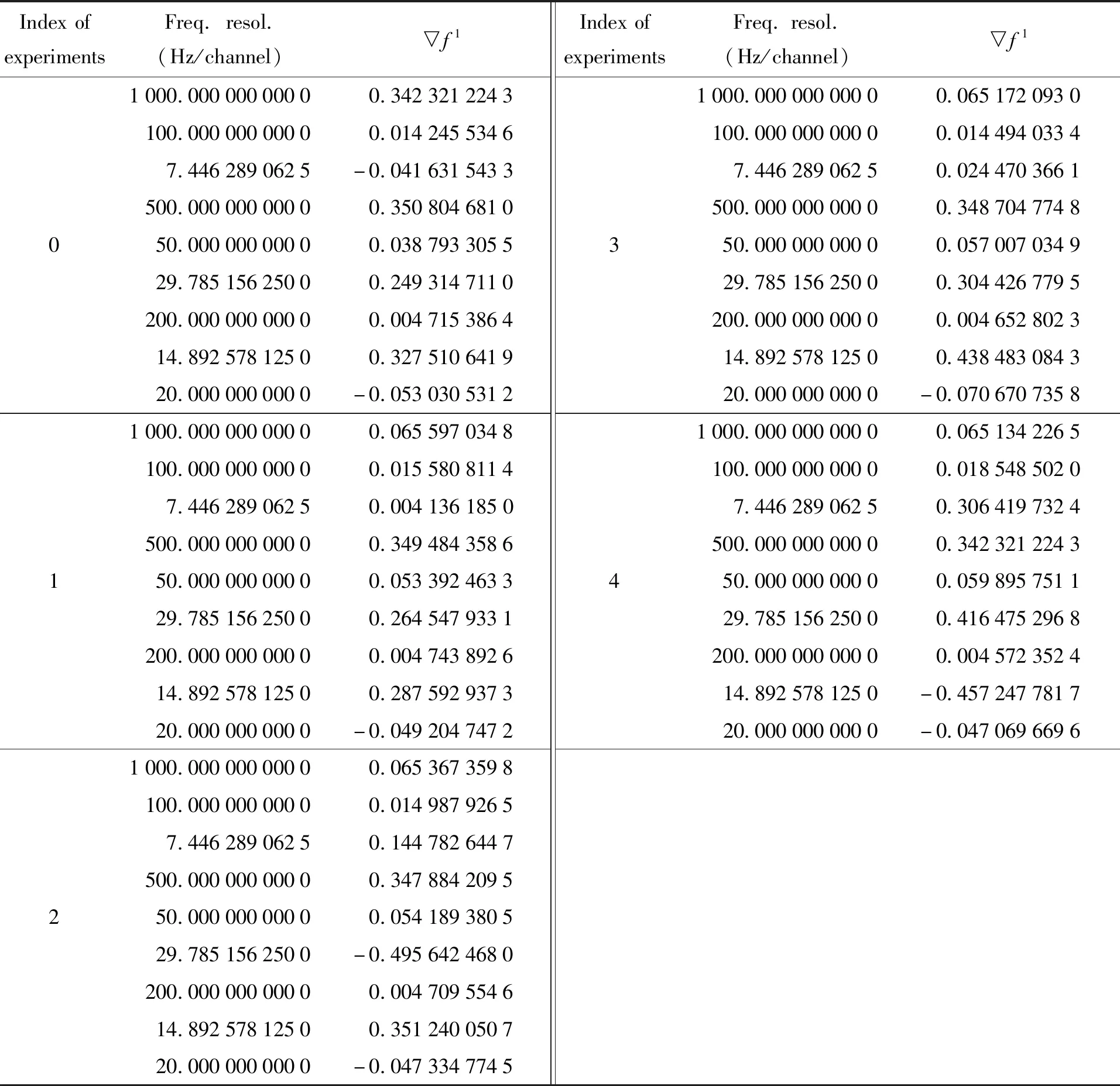




4 总结与展望
