掘进机截割部行星齿轮传动系统断齿故障仿真分析

2020-07-24胡亮赵国瑞李旭

矿业科学学报 2020年4期

胡亮，赵国瑞，李旭

1. 中国矿业大学(北京) 机电与信息工程学院，北京 100083；2. 天地科技股份有限公司开采设计事业部，北京 100013；3. 天地科技股份有限公司，北京 100013

悬臂式掘进机作为煤矿巷道综掘施工的主要设备，其运行状态直接影响掘进工作面的工作效率和掘进速度[1]。截割系统是掘进机实现煤巷断面掘进的关键部件，主要由截割电机、截割减速器、截割头组成。截割电机通过行星齿轮减速器将动力传递给截割头[2]。受煤层地质、煤岩性质、开采条件等因素影响，掘进机在工作过程中截割头承受较大的冲击载荷作用，导致截割减速器齿轮断齿等故障频发。

为提高掘进机的效率和安全可靠性，众多学者围绕掘进机故障诊断等相关技术进行了研究。陈慎金、杨健健、李旭等[3-5]基于微分几何原理研究了掘进机工作机构在巷道空间的运动响应。刘强等[6]采用故障树-层次分析法对某型号掘进机截割系统故障进行分析。杨健健等[7]提出了基于PSO-BP神经网络的掘进机截割部故障诊断方法。尹同舟等[8]通过井下实测工况数据对掘进机截割臂的振动信号进行分析，给出了井下掘进机的简易故障诊断方法。

国内外学者对行星齿轮系统动力学特性及故障诊断进行了大量研究，取得了丰富的成果[9-11]。冯志鹏等[12]对行星齿轮传动系统局部故障振动信号的频谱结构进行分析，得到了太阳轮、行星齿轮、齿圈发生局部故障特征频率。李晟等[13]建立了两级行星轮系非线性动力学模型，对其分岔和混沌特性进行研究。Shao等[14]对行星齿轮齿根裂纹故障的动力学响应特征进行了研究。张俊等[15]用动态子结构法建立考虑齿圈柔性的行星齿轮系统刚柔耦合动力学模型，对行星齿轮系统的固有特性进行了分析。Eritenel等[16]建立了单级行星齿轮系统三维模型，对系统的固有特性进行了分析。Kim等[17]考虑轴承变形引起的时变压力角和接触比的影响，建立单级行星齿轮系统的动力学模型，对其动态响应进行了分析。

由于计算机仿真和虚拟样机技术的发展，可通过建立齿轮传动系统的虚拟样机模型，实现对系统动力学响应特征进行分析[18]。毛君等[19]建立了采煤机截割部传动系统动力学模型，通过数值仿真研究了啮合刚度、阻尼等对齿轮系统动态特性的影响。陈昊坤等[20]对齿轮正常状态和裂纹故障时的接触应力进行有限元分析，对比应力云图得到裂纹对齿轮强度的影响。牛秋蔓等[21]基于ADAMS动力学仿真软件，通过编写cmd文件，分析了具有几何偏心齿轮的动力学响应特性。

由于煤矿井下特殊的工作条件，实际获取掘进机截割部完备故障案例比较困难。笔者在已有研究的基础上，详细阐述行星齿轮系统不同部件发生断齿故障时的响应特性，运用虚拟样机技术分别建立行星齿轮截割减速器齿圈断齿、行星齿轮断齿、太阳轮断齿故障模型，通过对仿真信号进行分析，揭示行星齿轮减速器在各种断齿故障状态下的动力学特性，为行星齿轮故障诊断提供依据。

1 故障行星齿轮系统动力学模型

1.1 ADAMS动力学理论

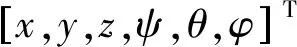
(1)

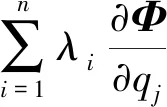
集成系统运动方程和约束方程，ADAMS可自动建立系统的动力学微分代数方程：

(2)

式中，Pq为系统广义坐标表示的动量；Φ为约束函数；Φq为约束方程的Jacobian矩阵；λ为拉格朗日乘子；H为外力坐标转换矩阵；F为系统所受外力；u为广义坐标对应的速度。

1.2 故障行星齿轮系统虚拟样机模型

掘进机截割减速器采用两级行星齿轮传动结构，由于低速级行星齿轮承受的扭矩载荷较大，同时受到截割头传递的冲击载荷作用，导致低速级故障率较高。笔者通过建立EBZ120型掘进机截割减速器低速级行星齿轮传动系统虚拟样机模型，对其断齿故障响应进行分析。

EBZ120型掘进机截割减速器低速级行星齿轮系统参数为：法向模数m为10 mm，压力角α为20°，螺旋角β为14°，齿圈的齿数Zr为58，行星轮(3个)的齿数Zp为19，太阳轮的齿数Zs为20。根据行星齿轮系统参数，在三维绘图软件SolidWorks中建立低速级行星齿轮传动系统各部件三维模型并进行装配，确保模型无干涉后将其导入ADAMS中。截割减速器低速级行星齿轮系统虚拟样机模型如图1所示。

图1 低速级行星齿轮系统虚拟样机模型Fig.1 Virtual prototype model of low-speed stage planetary gear system

为了研究断齿故障行星齿轮系统的动力学特性，建模时在相应齿轮切除部分轮齿模拟断齿故障(图2)，然后将断齿模型导入图1行星齿轮系统虚拟样机模型中，替换相应部件，分别建立行星齿轮断齿、太阳轮断齿、齿圈断齿、故障虚拟样机模型。

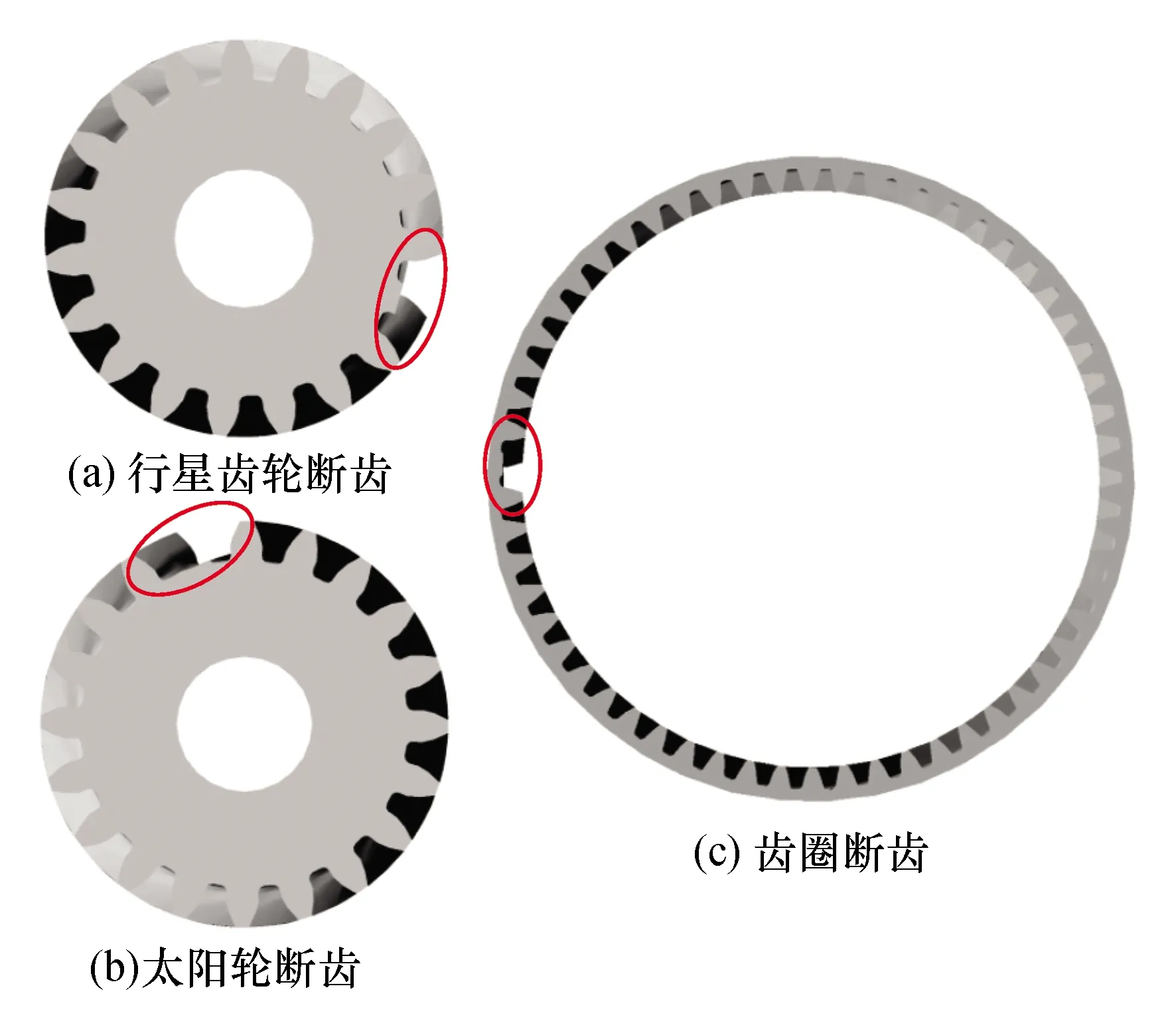
图2 齿轮断齿模型Fig.2 The model of gear with tooth break fault

1.3 传动比与特征频率

截割减速器低速级行星齿轮传动系统以太阳轮作为输入，齿圈固定，行星架作为输出。根据模型参数，低速级行星齿轮系统的传动比为

(3)

式中，ns为太阳轮转速；nH为行星架转速；Zr为齿圈齿数；Zs为太阳轮齿数。

EBZ120型掘进机截割减速器高速级行星齿轮系统传动比为5.88，截割电机的满载转速为1 470 r/min。计算得到低速级行星齿轮传动系统的输入转速ns=250 r/min，行星架输出转速nH=64.1 r/min，行星架的转速频率fH=1.07 Hz。齿轮的啮合频率与转速、齿数有关，在行星齿轮系统中太阳轮、行星轮、齿圈的啮合频率均为fm=fHZr=62.06 Hz。

齿轮发生断齿故障时，在断齿处齿轮的啮合会产生冲击振动。随着齿轮的转动，冲击按照一定的时间间隔重复出现。齿轮故障特征频率等于冲击序列的重复频率，即单位时间内故障轮齿与其他齿轮的啮合次数。

如果齿圈发生局部断齿故障，则在相对行星架的1个旋转周期内，齿圈故障轮齿分别与3个行星轮产生3次冲击。齿圈局部断齿故障对应的故障特征频率为

(4)

式中，fr为齿圈故障特征频率；fm为啮合频率；N为行星轮的个数，模型中N=3。

由式(4)得齿圈故障特征频率fr=3.21 Hz。

如果行星齿轮发生局部断齿故障，则在相对行星架的1个旋转周期内，行星齿轮故障轮齿分别与太阳轮和齿圈产生2次不同的冲击。行星齿轮局部断齿故障对应的故障特征频率为

(5)

式中，fp为行星齿轮故障特征频率；Zp为行星齿轮齿数。

由式(5)得行星齿轮故障特征频率fp=3.27 Hz。

如果太阳轮发生局部断齿故障，则在相对行星架的1个旋转周期内，太阳轮故障轮齿分别与3个行星齿轮产生3次冲击。所以，太阳轮局部断齿故障对应的故障特征频率为

(6)

式中，fs为太阳轮故障特征频率。

由式(6)得太阳轮故障特征频率fs=9.3 Hz。

2 动力学仿真计算

2.1 接触力计算

在ADAMS中设置接触参数模拟齿轮的啮合过程。假设相互接触的物体为刚体，接触过程满足Hertz接触理论。轮齿之间的接触力通过冲击函数法定义，计算公式为

(7)

式中，K为刚度系数；g为碰撞过程中两物体相互渗入的深度；e为碰撞指数；C为阻尼系数；step为阶跃函数；dmax为碰撞过程中最大允许穿透深度。

刚度系数K取决于相互碰撞物体的材料和结构形式，计算公式为

(8)

式中，R为综合曲率半径；E为综合弹性模量。

弹性模量可由式(9)、式(10)计算：

(9)

(10)

E1=E2=2.07×105MPa

式中，E1、E2为两个接触齿轮材料的弹性模量；μ1、μ2为两个接触齿轮材料的泊松比，μ1=μ2=0.29；R1、R2为两个接触齿轮接触点的当量曲率半径(内啮合取“-”，外啮合取“+”)。

根据经验，最大穿透深度dmax取0.02 mm，阻尼系数C取35 N/(s·mm)，碰撞指数e取1.5。

2.2 添加约束与驱动

在行星齿轮与行星架之间、行星架与地面之间、太阳轮与地面之间添加转动副；齿圈与地面之间添加固定副；齿圈与行星齿轮、行星齿轮与太阳轮之间添加接触。

由1.3节计算得到低速级太阳轮的输入转速为250 r/min。为避免仿真开始时速度发生突变，以step函数形式在太阳轮上添加速度驱动在0.2 s时达到目标转速。行星架上受到的负载转矩为

(11)

式中，P为截割功率，P=120 kW；n为截割头转速，n=nH=64.1 r/min。

由式(11)得到行星架上的负载转矩T=1.79×107N·mm。

以step函数形式在行星架上添加负载转矩为1.79×107N·mm，方向与输入转速方向相反。

2.3 模型求解

ADAMS中采用变系数的BDF刚性积分法对式(2)的动力学微分方程进行求解。BDF刚性积分方法是一种自动变阶、变步长的预估校正法，主要分为预估阶段、校正阶段和误差控制阶段。

在预估阶段，根据当前时刻的系统状态矢量值，用泰勒级数预估下一时刻系统的状态矢量值：

(12)

式中，h为时间步长，h=tn+1-tn。

这种预估算法得到的新时刻的系统状态矢量值通常不准确，可以由Geark+1阶积分求解程序来校正，即

(13)

式中，yn+1为y(t)在t=tn+1时的近似值；β0和αi为Gear积分程序的系数值。

式(13)经过整理，可以表示为

(14)

在误差控制阶段，对状态向量的预测值与校正值进行比较，如果误差过大，则舍弃此解；如果误差在允许范围内，则接受此解。不论误差大小都要对步长h和阶数n进行求解，直到达到仿真结束时间方可停止。

3 仿真结果分析

图3为行星齿轮传动系统太阳轮输入转速和行星架输出转速随时间变化曲线。从图3中可以看出，输出转速在0.2 s以后趋于稳定，其均值为64.10 r/min。根据输入转速和传动比计算得到的行星架输出转速为64.10 r/min，仿真结果与理论计算结果相吻合，证明所建模型正确。

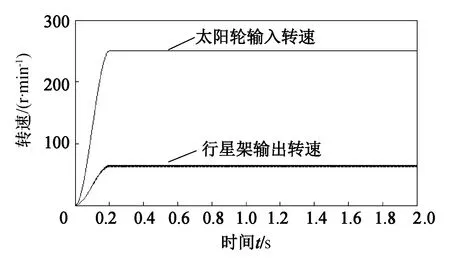
图3 行星轮系输入输出转速Fig.3 Planetary gear transmission input/output speed

工程上，掘进机截割部振动监测所用传感器通常安装在轴承以及箱体上靠近齿圈等振幅较大的位置，箱体安装在回转台上，齿圈与箱体固连在一起。假设回转台的支撑刚度足够大，建模时以回转台作为地面参考坐标系，齿圈与箱体之间的固定约束通过定义齿圈与地面之间的固定约束模拟。本文以齿圈约束反力作为研究对象，表征行星轮系正常状态、齿圈断齿故障、行星齿轮断齿故障、太阳轮断齿故障时系统响应特性，如图4所示。

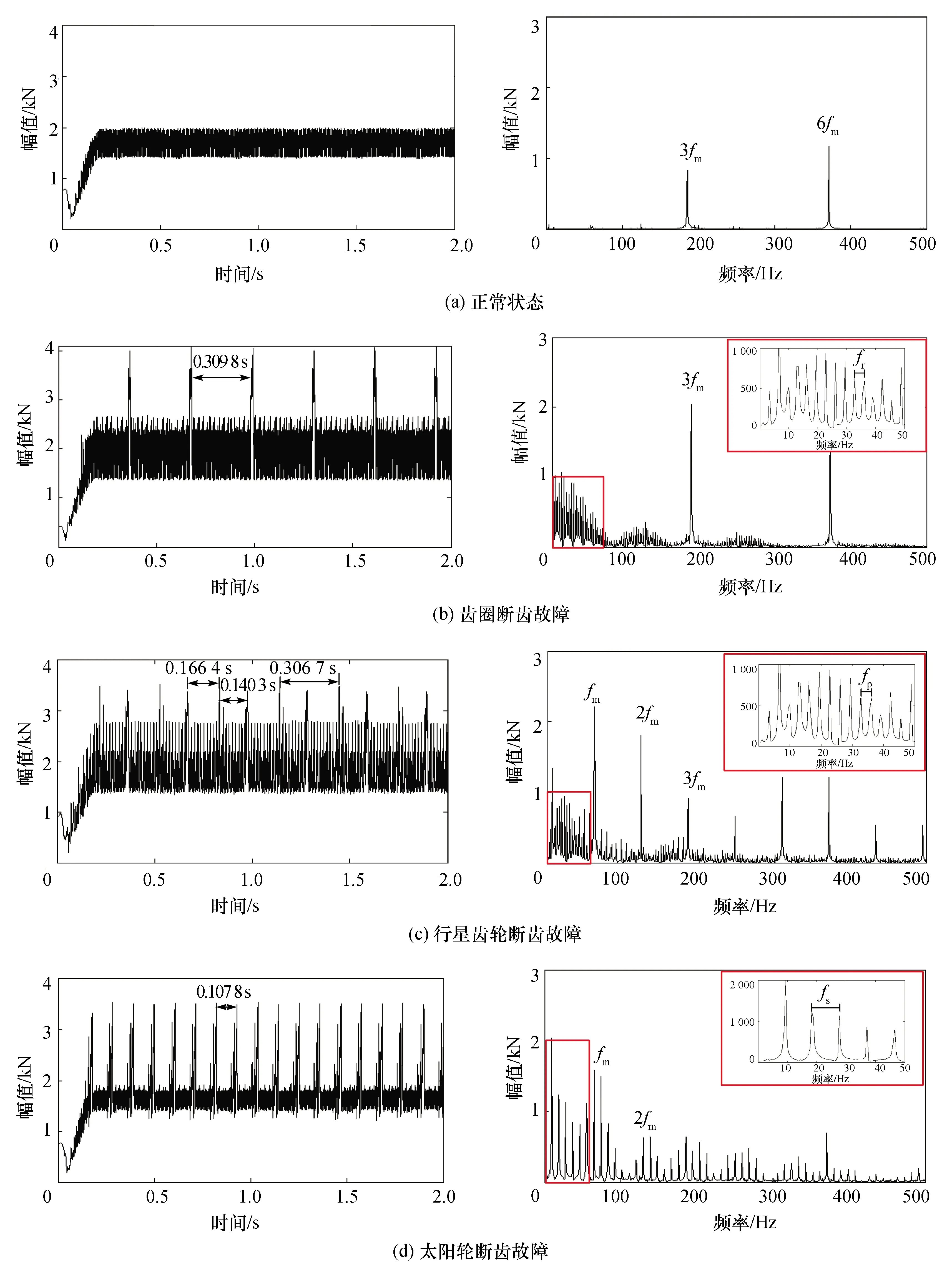
图4 齿圈约束反力时域波形及幅值谱Fig.4 Time-domain waveform and amplitude spectrum of ring gear restraint reaction

图4(a)为正常状态下齿圈约束反力时域波形与幅值谱。齿圈约束反力的时域均值为17.134 kN，齿轮周期性啮入、啮出的特点导致约束反力的幅值在13.816～19.867 kN波动。从幅值谱中可以看出，行星轮系啮合频率的3倍频和6倍频谱线比较突出。

图4(b)为齿圈发生断齿故障时齿圈约束反力时域波形与幅值谱。齿圈约束反力的时域均值为20.605 kN，时域波形中含有明显的周期性冲击成分，冲击间隔为0.309 8 s(3.23 Hz)。幅值谱中主要包含啮合频率的3倍频和6倍频成分，同时在低频处产生明显的边带成分，边带带宽为3.23 Hz，对应齿圈局部故障特征频率。

图4(c)为行星齿轮发生断齿故障时齿圈约束反力时域波形与幅值谱。齿圈约束反力的时域均值为18.413 kN，时域波形中含有2组周期性冲击成分，对应行星齿轮转动一圈与齿圈和太阳轮产生2次不同的冲击，周期性冲击的间隔为0.306 7 s(3.27 Hz)。幅值谱中主要为啮合频率及其倍频成分，在低频处产生明显的边带成分，边带带宽为3.27 Hz，对应行星齿轮局部故障特征频率。

图4(d)为太阳轮发生断齿故障时齿圈约束反力时域波形与幅值谱。齿圈约束反力的时域均值为17.886 kN，时域波形中包含有明显的周期性冲击成分，冲击间隔为0.107 8 s(9.28 Hz)。幅值谱中包含有明显的边带成分，边带带宽为9.28 Hz，对应太阳轮局部故障特征频率。