富水软弱层联络通道冻结温度场研究
2020-07-24朱现磊
朱现磊
中国矿业大学(北京)力学与建筑工程学院,北京 100083
人工冻结法具有强度高、隔水性好、无污染及对复杂地层适应性强等特点,被广泛应用于矿山、隧道开挖、地铁联络通道等工程[1]。然而,人工冻结法施工时土体冻胀效应会对冻结管周围的地下管线、地表建筑及交通等产生不利影响,因此须控制冻胀的影响范围[2]。冻结温度场是冻结壁形成、发展变化的基础,是控制土体冻胀的关键。
国内外学者对人工冻结温度场进行了大量研究。王延波等[3]运用解析计算的方法,对积极冻结期冻结壁平均温度等参数求出了解析解;胡向东等[4-6]对单双排管冻结温度场算式进行了完善和应用性研究,获得了环形冻结管中的单圈管冻结温度场解析解;Hansson等[7]通过高寒冰冻土路基解冻实验室与现场研究,得出了适用的计算模型;孙强等[8]采用模型试验和数值模拟,得到了新型冻结器的温度场时空分布特征;袁云辉等[9-10]使用等有限元软件对冻结法施工联络通道冻土体温度场进行了研究;杨维好等[11-12]通过室内模型试验研究不同参数对冻土冻胀性影响;Zhou等[13]研究了温度稳定时冻胀速率与温度梯度的关系;Klinova等[14]研究了含水率、孔隙率等对土体融沉特性的影响;戴华东等[15]研究了温度场等参数对冻土力学性能的影响;岳丰田等[16-17]介绍了对联络通道冻结工程冻结期间的冻土结温度场的实测和分析。
在实际冻结过程中温度场的演化具有三维空间效应,已有的研究多以二维模型试验为主,不能很好地反映冻结现场温度场的空间变化规律。同时,对富水黏土复杂条件下冻结法施工的温度场变化规律,有待进一步研究。本研究以富水软弱地区联络通道为工程背景,运用大型三维人工冻结试验系统,结合数值模拟和解析解计算,进行人工冻土温度场研究,为富水黏土复杂条件下联络通道的冻结施工提供理论和技术参考。
1 人工水平冻结土体温度场模型试验
1.1 工程背景
某城市地铁联络通道位于流塑状的粉质黏土层及粉土层中,由于近海,地下水埋藏浅,水量丰富,水位标高一般为-1.1~-3.6 m,无地下流动水源。土层强度低,地面为城市既有建筑和市内道路,设计采用人工水平冻结暗挖法施工。
本工程采用盾构法施工,联络通道处地面标高+3.24 m,左右线隧道中心标高-14.63 m,盾构隧道中心距19.12 m。隧道直径6.2 m,衬砌采用预制钢筋混凝土管片,管片内径5.5 m,混凝土强度等级C55,抗渗等级≥S10。联络通道的水平通道为直墙圆弧拱结构,开挖轮廓高5.1 m,宽4.1 m,开挖区标高范围为-12.5~-18.7 m。
1.2 模型试验系统
试验采用2 m×2 m×2 m的三维模型试验系统,系统箱体内可实现水平和垂直方向加载。冻结由制冷压缩、制冷剂循环、冷媒循环和温度监测系统组成。制冷系统最大制冷量大于6.3 kW,最低冻结温度-35 ℃,冷媒为CaCl2溶液。冷媒循环系统由低温水泵、分水器、高压橡胶管、冻结管等依次连接组成。温度变化由温度传感器监测,由万用表采集温度数值。
1.3 试验方案
1.3.1 模型相似比及参数设计
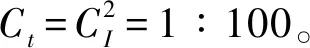
1.3.2 边界条件的模拟
岩土自重荷载和围压是冻结壁形成的必要条件。按照圣维南原理,模型试验时施加等效荷载冻结,模型冻结壁与原型冻结壁形成的力学条件是相似的,因此其强度和应力也是相似的。模型冻结壁与原型冻结壁的傅里叶准则数相等时,将得到模型与原型“自模拟”。
1.3.3 模型材料的确定
选取与现场河床-河漫滩相沉积层相近的粉质黏土,分别采用称重法(烘干法)、环刀法和固结试验法,获得试验土体的含水量、密度、内摩擦角等物理力学指标,具体参数见表1。

表1 相似土体物理力学参数
1.3.4 冻结管及测点布置
模型冻结管与联络通道近似平行布置,如图1所示,共布置20根冻结管D1—D20,间距100 mm,在联络通道模型周边布置共8个测点C1—C8,其中C1—C4为第一测区,C5—C8为第二测区。各测点分别埋装温度传感器,Cn处的温度用Tn表示。

图1 冻结管及测点布置Fig.1 Freezing tube and measuring point map
1.3.5 试验温度控制
传感器及模型埋设完成后放置7 d进行固结。在室温16 ℃下开始试验,开机冻结前压缩机和高压泵预热4 h。开机约12 h冷媒(CaCl2溶液)温度达-25 ℃,进入冻结维护期,冷媒温度控制在-25 ℃~-23 ℃。约7 h后冻结帷幕形成,进行联络通道开挖(图2),开挖完毕即压缩机关闭后进行自然解冻。

图2 土体开挖图Fig.2 Excavation picture
1.4 试验结果分析
1.4.1 冷源与回路温度变化
从图3冷源与回路温度变化可以看出,压缩机开机后冷源温度迅速下降,经过4 h的温度骤降,温度变化开始趋缓,冷媒与土体的热交换逐渐增多,约12 h达到预设温度值,并进入维持冻结期,此时冷源与回路的温差值稳定在1 ℃左右,说明冷媒与土体的热交换基本稳定。
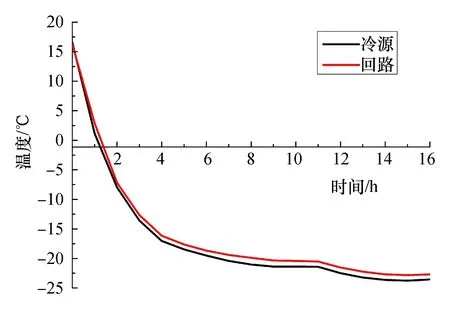
图3 冷源与回路温度对比Fig.3 The temperature comparison of CaCl2 solution before and after passing the soil
1.4.2 冻土温度场变化分析
从图3可知,4 h冷源温度达到了-17 ℃,约12 h达到预设温度-25 ℃,表明模型积极冻结时间为12 h。从图4测点温度变化可知,约19 h后土体冻结帷幕形成,模型维护冻结时间7 h。根据时间相似比,可知工程现场的积极冻结时间为50 d,维护冻结时间为29 d。
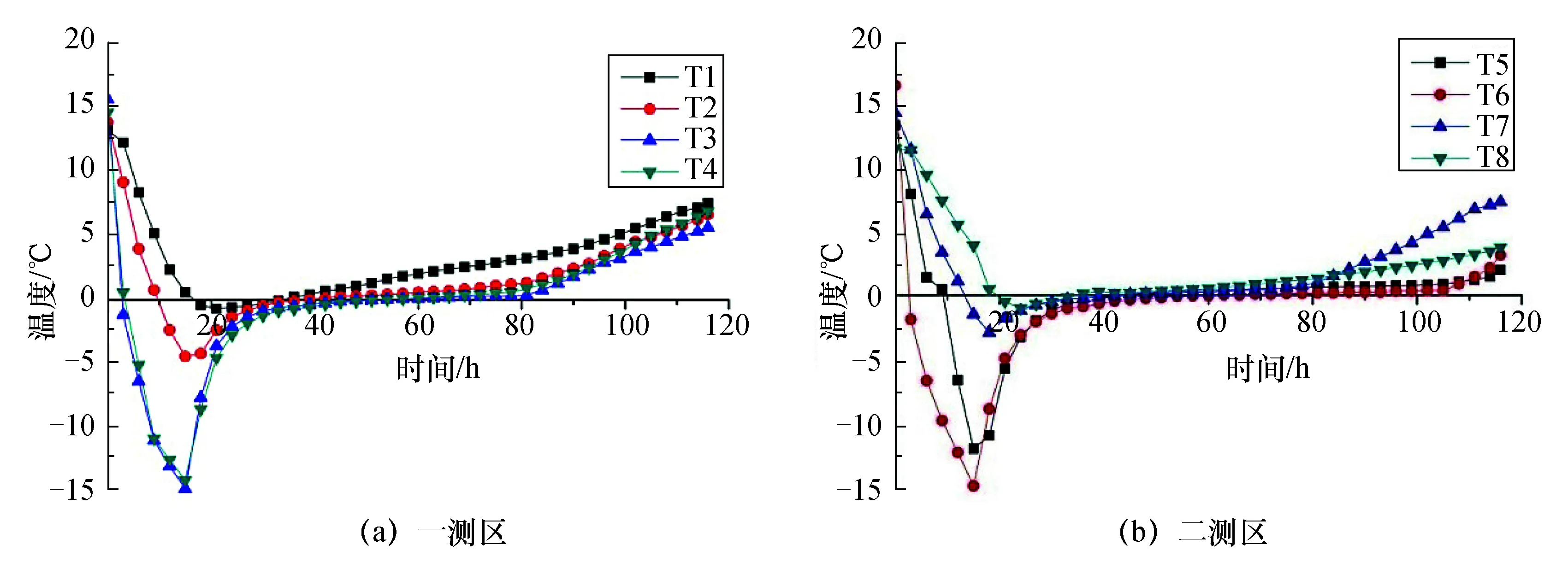
图4 不同测区、测点温度变化分析Fig.4 Comparative analysis of temperature in different survey areas and measuring points
在整个冻融过程中,随着时间的增加,土体温度先迅速降低,冻结结束后迅速增加,然后在0 ℃左右维持冰水状一段时间,最后温度再次升高。积极冻结期,在低温冷媒作用下,冻结管周边土体发生相变,温度迅速下降,然后冻土锋面向远冻结管方向继续扩展,冻结速度趋于平缓。故同一测区内测点C3、C6距离冻结管更近,土体冻结更快,温度降幅更大,最低温度达-15.2 ℃。同时,测点C1温度变化较小,最低温度约为0 ℃。冻土融化阶段,冻土温度升高至0 ℃,土体中结晶水开始融化,并维持冰水状一段时间,待结晶水完全融化后,土体温度继续升高。整个融化过程所需时间约为冻结过程所需时间的3~4倍,由于埋深较大,二测区冻土的融化时间更长。
2 人工水平冻结土体温度场数值分析
2.1 模型建立
以某城市地铁联络通道冻结现场为依据,利用ANSYS有限元分析软件建立冻结—开挖—解冻温度场数值计算模型,如图5所示。由于模型具有对称性,故取一半进行模拟分析。模型共有单元8 020个,节点8 180个。数值计算模型土体的物理力学参数列于表2。
图5 数值计算模型Fig.5 Numerical calculation model
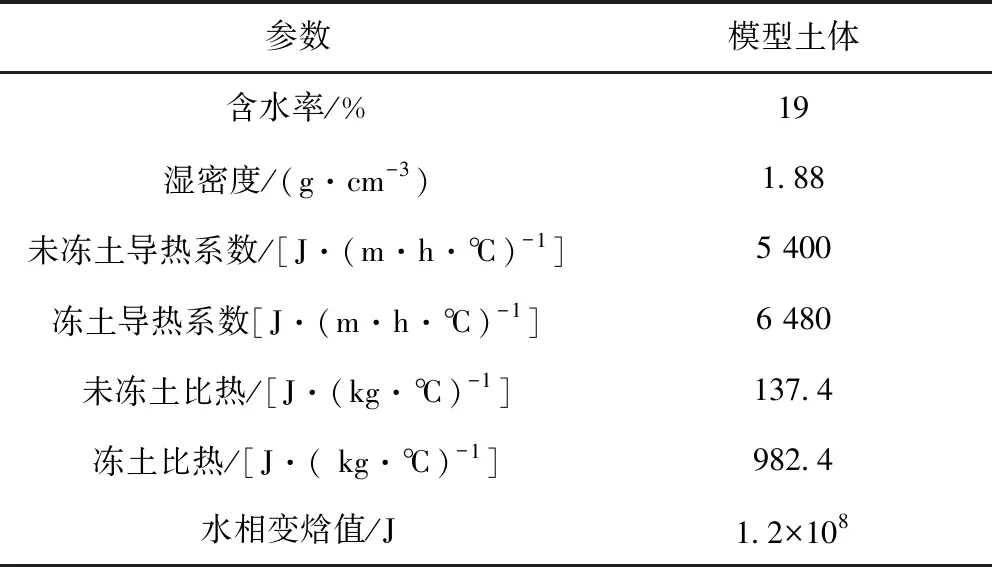
表2 数值计算模型土体的物理力学参数
2.2 边界条件
模型左边界为对称边界,设置为绝热边界,上下边界和右边界设置为固定环境温度10 ℃。冻结开始时,根据模型试验中实际盐水温度制定数值模型中各模拟时间的冻结管温度值。待积极冻结12 h后开始开挖联络通道,并于联络通道边界施加环境温度荷载为10 ℃。盐水冻结—解冻计划见表3。
2.3 数据分析
联络通道冻结—开挖—解冻过程不同时刻模型温度场云图如图6所示。冻结1 h后冻结管开始交圈,冻结5 h已全部交圈,但冻结壁内部核心位置还处于正温状态。积极冻结12 h后开始开挖,此时冻结壁内圈已全部进入负温状态。此后由于通道暴露在空气中,通道四周温度逐步升高并向冻结壁内部发展。维护冻结20 h后,冻结系统不再制冷,盐水温度逐步升高,进而导致冻结壁温度也不断升高;40 h后,冻结壁区域基本完全解冻,最低温度为-1 ℃。
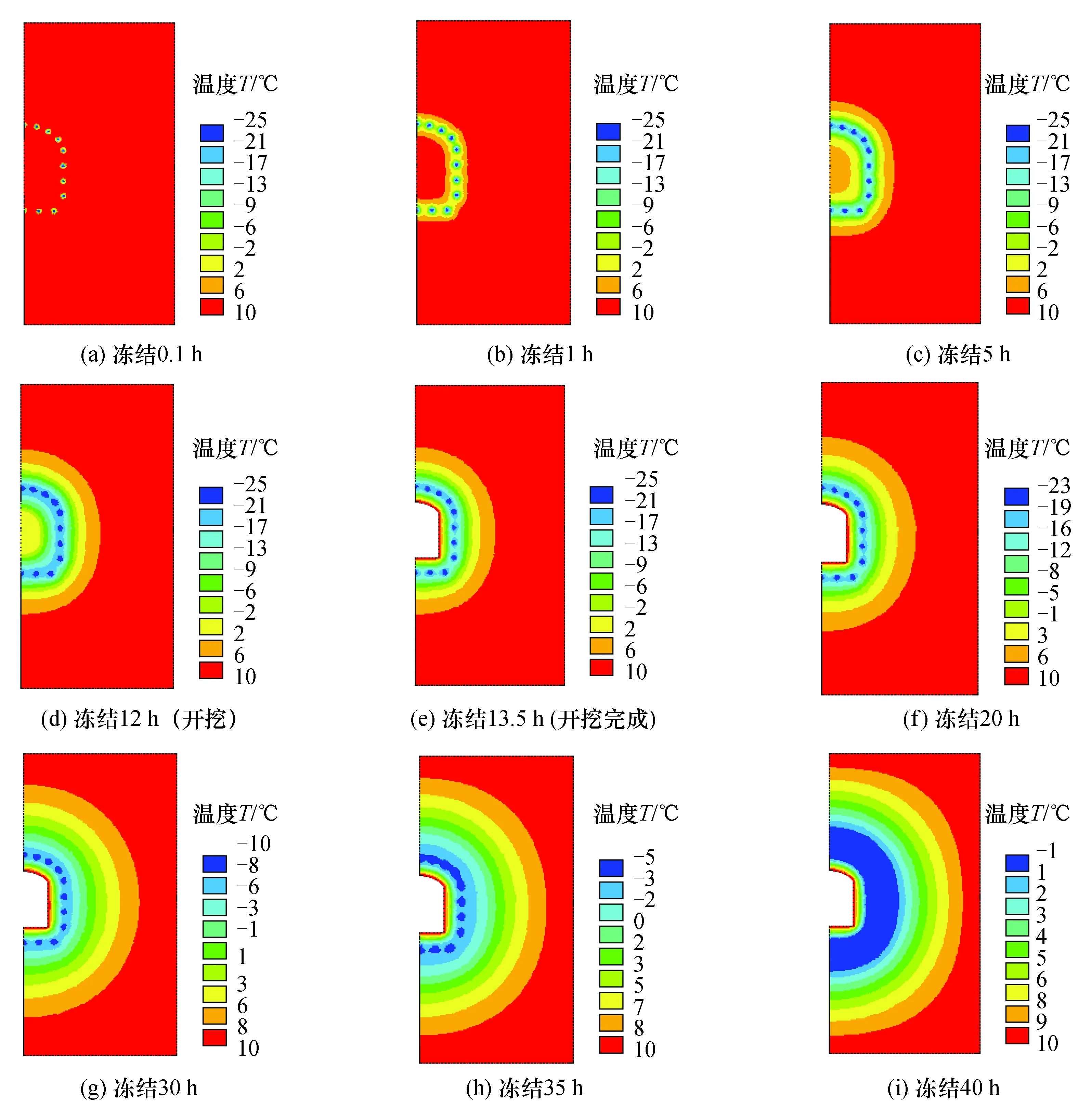
图6 冻结各时段模型温度云图Fig.6 Model temperature cloud map of freezing periods
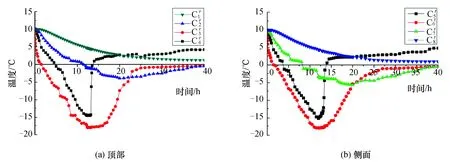
图7 通道测点温度变化规律Fig.7 Temperature variation
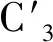
3 冻结温度场的解析解
3.1 单管冻结温度场解析解
特鲁巴克假设冻结温度场为稳态的二维温度场,以二维拉普拉斯方程的极坐标形式作为其稳态导热方程,得到无限长圆管的导热方程为[18]
(1)
边界条件为
r=r1,t=tyr=r2,t=tD=0
(2)
解得
(3)
式中,t为冻结壁中距离冻结管轴线r处的温度;ty、tD分别为冻结管外表面温度和冻土温度;r、r1、r2分别为计算点至冻结管中心距离、冻结管外半径和冻结壁半径。
由式(3)可知,沿冻土墙横截面的主面冻土温度为对数曲线分布。
3.2 双管冻结温度场解析解
冻结管轴向尺寸较径向大得多,热传导较径向也弱得多,故将冻结温度场简化为平面导热问题。假设冻结管O1在冻结管O2预先形成的温度场内冻结而成,计算示意图如图8所示。
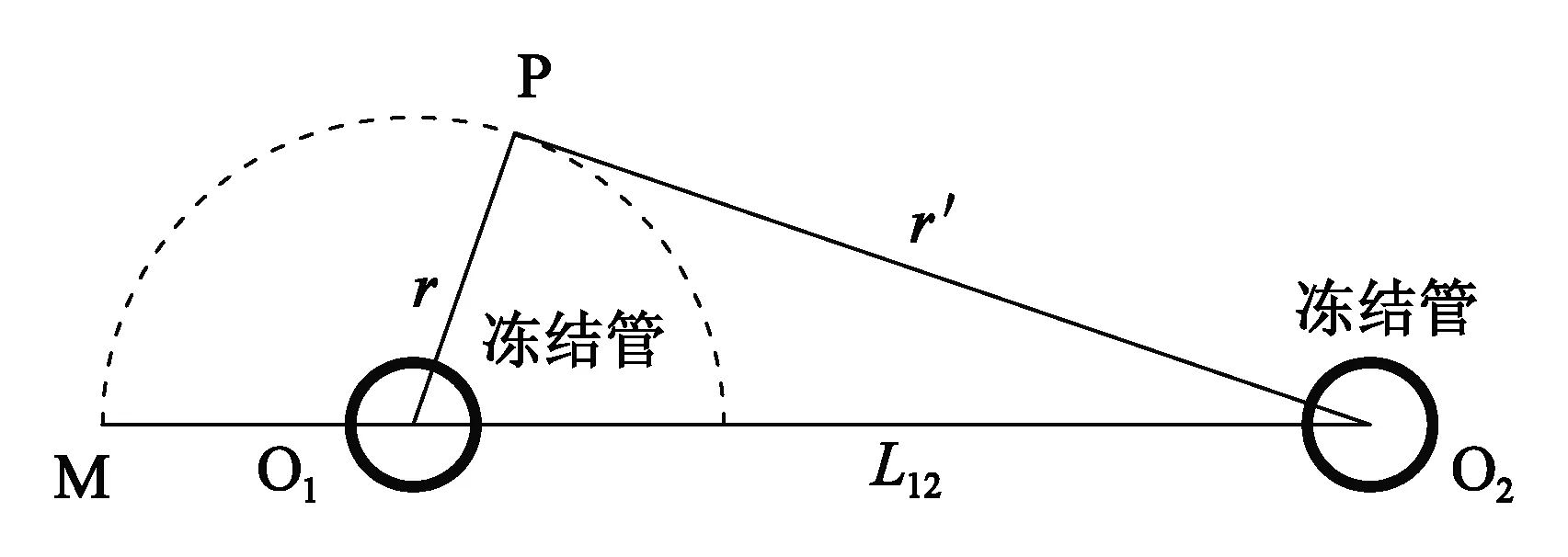
图8 双管冻结温度场解析解计算示意图Fig.8 Schematic diagram of analytical solution calculation for double tube freezing temperature field
冻结温度场内,距离冻结管O1中心等距的M和P两点,M至O2的距离为相对O2最远一点,在冻结管O2的影响下,距离O2较近的P点起始温度更低,M和P两点达到相同温度的温降值也不同。P点的温降系数
φP=qP/qM
(4)
qP=ΔTP/R
(5)
qM=ΔTM/R
(6)
(7)
ΔTP=tPO2-t1
(8)
ΔTM=tMO2-t1
(9)
式中,qP与qM分别为圆筒壁面上P、M点的热流量;R为圆筒壁的导热热阻;λ为导热系数;ΔTP、ΔTM为P(M)点受O2影响的温度tPO2、tMO2与受O1影响的温度t1的温差。
根据式(3)单管冻结温度场解析解可知
(10)
(11)
将式(5)至式(12)代入式(4),得P点的温降系数为
(12)
P点受O2影响温度变化为φp(tMO2-tPO2)。
故任一点P的双管冻结耦合温度为
t=tPO1-φp(tMO2-tPO2)
(13)
将各值分别代入,由此可建立双管冻结下的温度场计算方法为
(14)
式中,t1为冻结管外表温度;r为计算点至冻结管O1的距离;r′为计算点至冻结管O2的距离;L12为冻结管O1至O2的距离。
4 结 论
以某富水软弱地层地铁联络通道冻结工程为研究背景,运用室内模型试验、有限元数值模拟相结合的方法对冻土温度场进行研究,并求解冻结温度场解析解,得到的主要结论如下:
(1) 冻结试验开始后12 h达到预设温度-25 ℃,19 h土体冻结帷幕形成,根据时间相似比,可得联络通道冻结工程现场的积极冻结时间为50 d,维护冻结时间为29 d。
(2) 土体冻结过程中,温度变化大致分两个阶段,第一阶段土体温度呈线性快速下降至0 ℃,第二阶段土体相变放热后,温度继续下降,最低温度为-15.2 ℃~-16.8 ℃。整个过程中,土体降温速度呈现先快后慢态势。
(3) 随着联络通道的开挖,冻结圈内冻结壁温度显著升高,应及时对开挖联络巷进行有效支护,冻结圈外冻结壁温度受开挖影响较小。
(4) 基于单管冻结温度场的解析解,推导得到了双管冻结温度场解析解。
