基于改进动态时间规整算法的奶牛步态分割方法

2020-07-24苏力德宗哲英巩彩丽

农业机械学报 2020年7期

苏力德张永王健尹玉宗哲英巩彩丽

(1.内蒙古农业大学机电工程学院，呼和浩特 010018； 2.内蒙古大学电子信息工程学院，呼和浩特 010021)

0 引言

内蒙古自治区是我国重要的奶牛养殖优势区域，其奶牛存栏数、牛奶产量，以及乳制品企业的规模、效益和影响力均位于全国前列。据我国奶业年鉴统计，截止到2017年，奶牛存栏数已达到216万头，牛奶产量达到730万吨，乳制品产量达到337万吨。奶牛疾病阻碍了奶业的健康发展，据统计，我国大中型牧场临床跛行率和严重跛行率分别为(31±12)%和(10±6)%[1]。跛行不仅导致奶牛身体状况下降、牛奶产量降低，还将使奶牛过早地被淘汰。因此，准确分割奶牛步态、识别奶牛跛行对减少养殖场的经济损失、提高福利化养殖水平具有重要意义。

步态由周期性的步幅组成，如何从步态序列中分割单个步幅已成为运动分析领域的研究热点。国内外学者主要采用峰值检测法[2-3]、视频分割法[4]、模板匹配方法分割步态。峰值检测法必须满足一定的阈值条件才可以进行分割；视频分割方法工作量大、自动化程度不高，限制了在实际中的应用；模板匹配方法通过计算两个时间序列之间相似程度对步态进行分割。国内外基于模板匹配方法的步态分割主要集中在人体步态研究，对奶牛步态分割的研究尚未见报道。文献[5-6]利用基于模板匹配的互相关方法对人体步态进行分割，但步幅模板长度和形式固定，不适用于不同步幅长度序列的分割。

动态时间规整算法(Dynamic time warping,DTW)是一种非线性匹配算法，该算法来源于动态规整原理，解决时间长度不一致时的模板匹配问题。文献[7]利用动态时间规整算法对人体步态进行分割，通过研究步态周期数据间的差异性，证明该方法在临床疾病检测上优于其他方法。文献[8]利用传感器技术采集步态信息，以动态时间规整算法分割步态，通过k近邻分类器对偏瘫患者进行识别，得出曲线下面积为0.94。文献[9]利用动态时间规整算法对帕金森患者步态进行分割，获得100%的分割准确率。文献[10]利用动态时间规整算法对25名老年人的步态进行分割，分割准确率达到97%。

常规的动态时间规整算法样本序列是一维数据，而奶牛步态加速度信号的时间和幅度是周期性变化的。本文利用三维加速度传感器采集奶牛趾蹄加速度信号，将时间和幅度组成的二维数据作为步态序列，提出一种改进的动态时间规整算法，对奶牛步态进行分割，并对每个步幅提取步态特征，利用Wilcoxon秩和检验分析健康奶牛和跛行奶牛特征值之间的关系，选取与跛行相关的6个特征，利用逻辑回归方法建立跛行识别模型，以准确识别奶牛的跛行。

1 材料和方法

1.1 测量设备

实验场地为内蒙古旗帜牧业有限公司，选择牧坤电子科技有限公司生产的M63X系列三维加速度传感器，测量范围±8g，采样频率50 Hz。将传感器封装在密闭防水盒，固定在制作好的绑带上，形成可穿戴式设备。数据通过ZigBee协议无线传输到基站，并实时上传到计算机。奶牛进入长、宽分别为23、0.8 m的测试通道，射频识别阅读器识别身份信息，使用PCO.dimax系列高速摄像机拍摄奶牛行走视频，如图1所示。由于奶牛85%的趾蹄疾病发生在后趾外侧爪上[11]，因此将加速度传感器绑在后肢外侧，为避免奶牛应激反应产生的测量误差，每头牛绑上加速度传感器行走10 min后开始采集，以此适应测量设备。

图1 测试环境及设备Fig.1 Test environment and equipment1.加速度测量装置 2.捆绑式加速度传感器 3.无线接收基站

1.2 数据采集与预处理

数据采集使用实验室虚拟仪器工程平台(Laboratory virtual instrumentation engineering workbench，LabVIEW)实时显示在上位机，LabVIEW与Access数据库连接实现对数据的管理，数据处理及算法实现通过Matlab软件编程，并与LabVIEW的DLL(Dynamic-link library)及ActiveX等技术实现混合编程。选取30头荷斯坦奶牛，其中健康奶牛21头、跛行奶牛9头，在测量通道内连续采集6 d，每天上午和下午挤完奶各采集一次，每次重复采集一次。为确保数据的准确性高速摄像机与加速度传感器系统实现同步采集，其中高速摄像机以940 f/s速率拍摄奶牛行走视频，并以该视频数据作为黄金标准。3名兽医通过观察每头奶牛行走视频，以5分制[12]评分规则对其进行评分，取平均值作为跛行评分值。在三维加速度传感器中，定义X轴为垂直方向、Y轴为前进方向、Z轴为水平方向。

由于噪声的存在，加速度数据不能直接应用于步态分割中，需对其进行预处理。小波变换去噪方法能有效区分信号突变部分和噪声[13]，本文通过小波变换方法对加速度数据进行预处理。利用Matlab软件在Daubechies小波基框架内，选择DB(Daubechies)6小波进行3层分解，通过信号重构去除干扰信号。

2 改进动态时间规整算法步态分割实现

将连续的步态序列分割为单个步幅称为步态分割。对于周期性步态的分割相对简单实现，然而在现实中步幅并不完全是周期性的，不同跛行评分、不同体质量和泌乳的奶牛步幅行走模式均有所不同。这些异构的步态序列是步态分割的主要难点之一，而动态时间规整算法主要解决序列长度不一致时模板匹配的问题，适用于不同行走模式下的步态分割。奶牛步幅定义为同一肢体连续2次接触地面之间的间隔，对应的时间差为一个步态周期。步态周期分为支撑阶段和摆动阶段，其中，在支撑阶段，趾蹄与地面接触开始，并在推开后终止。在摆动阶段，趾蹄需在地面以上抬起。一个步态周期中，摆动时间占31.6%，支撑阶段占68.4%[14]，平均步态周期为(1.22±0.05) s[15]。通过前期实验分析可知，利用垂直方向加速度信号分割步态容易存在误差，而水平加速度很大程度上受到乳房的影响，整个步行过程中变化并不明显。前进方向加速度信号极大值点突出容易区分，本文采用该方向加速度信号对步态进行分割。

利用动态时间规整算法分割步态是通过求模板样本序列映射到测试样本序列的成本距离，利用递推公式计算满足最小累积成本的规整路径，寻找与模板样本相似的子序列，最终从连续的步态序列中分割单个步幅。本文算法的步态分割整个流程如图2所示。

图2 步态分割算法流程图Fig.2 Flow chart of gait segmentation algorithm

2.1 步态序列特征点提取

奶牛一个步态周期中趾蹄触地和足底离地时刻前进方向加速度信号均有极值出现，利用小波变换过零点方法提取信号极值点[16-17]，并将该点作为样本特征点构成样本序列。信号突变点检测是对原始信号进行“磨光”的过程，磨光可以理解为对信号进行平滑处理[18-19]。磨光函数计算公式为

(1)

式中θ(t)——低通滤波器

假设θ(t)二次可导，对其求导表示为

(2)

函数ψ(1)(t)和ψ(2)(t)满足小波容许条件，可作为小波基函数，以此定义的卷积型小波变换为

(3)

式中 *——卷积运算符号s——尺度因子

θs(t)——θ(t)在s下的伸缩

f(t)——原始信号

2.2 模板样本建立

将连续步态序列定义为测试样本序列，向量表示为Q=(q(1),q(2),…,q(m))，其中m为序列长度。模板样本向量表示为P=(p(1),p(2),…,p(n))，其中n为序列长度。由于不同跛行程度的奶牛行走模式不同，将步态样本分为健康、轻度跛行、中度跛行和严重跛行4个组。根据高速摄像机拍摄的视频手动分割步态，将每个步幅起点和终点手动标记为模板和黄金标准。为建立能代表大范围步幅的模板序列，每组手动标记的步幅通过Matlab的interp1函数线性内插至各组样本中，并取平均值生成模板序列，待分割的测试样本及生成的模板样本如图3所示。

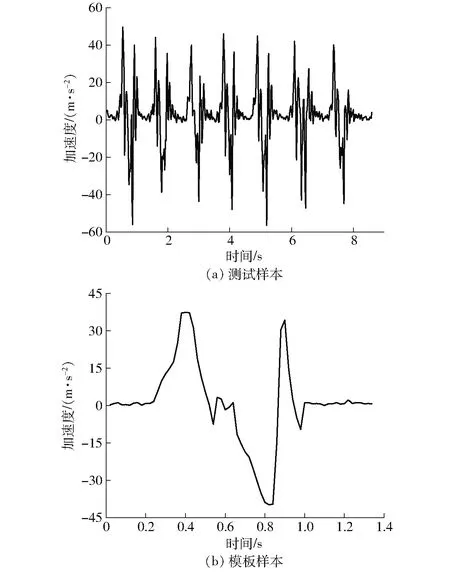
图3 模板样本与测试样本Fig.3 Template sample and test sample

2.3 累积成本矩阵计算

为计算2个不同样本序列的最小规整路径，构造了一个N×M的最小距离矩阵D。该矩阵中的每行表示模板样本的一个序列到测试样本的一个序列之间的距离。如果2个样本序列相似，则局部距离d较小，规整成本较低。相反，序列不相似，则d较大，规整成本较大。本文使用欧氏距离计算局部距离，计算公式为

(4)

式中p(n)——模板样本序列元素

q(m)——测试样本序列元素

为了寻找模板样本与测试样本间最小规整路径，定义了一个N×M的累积成本矩阵C。该矩阵表示模板样本映射到测试样本各个部分的累积成本，是通过距离矩阵建立累积成本矩阵来搜索最佳规整路径的。将距离矩阵D的第1列元素值依次求和得到累积成本矩阵C的第1列元素。而矩阵C的第一行元素由矩阵D的第1行构成，定义该行为起始行，用于计算模板样本映射到测试样本的累积成本。累积成本矩阵其余元素计算公式为

C(n,m)=d(n,m)+
min(C(n-1,m-1)，C(n-1,m)，C(n,m-1))

(5)

由式(5)可知，其可以通过将累积成本矩阵C3个方向的最小成本元素与距离矩阵D的各个元素相加来计算。因此，累积成本矩阵中元素表示模板样本映射到测试样本的最小累积成本。

2.4 算法改进

由于奶牛前进方向加速度信号极值是随时间周期性变化的，即每个步态周期特征点是由时间序列和幅度序列构成的二维序列。本文将该二维序列距离作为改进动态时间规整算法的局部距离。设模板样本的时间为pt，幅值为pa，测试样本的时间为qt，幅值为qa，因此，样本序列分别为Ps={(pt(1),pa(1)),(pt(2),pa(2)),…,(pt(n),pa(n))},Qs={(qt(1),qa(1)),(qt(2),qa(2)),…,(qt(m),qa(m))}，将式(4)中的p(n)和q(m)用该二维序列来代替，二维欧氏距离计算公式为

(6)

在将式(6)代入式(5)中，计算模板样本映射到测试样本的累积成本矩阵。

2.5 最小规整路径确定

最小规整路径反映2个样本相似性的同时可以确定步幅的分割起点及终点。将规整路径定义为W，该路径由成本距离矩阵的每一行元素局部最小值构成，计算公式为

W=(w1,w2,…,wk，…，wK)

(7)

式中K——路径长度

wk——路径中的点元素

k——测试样本序列长度

假设w0为规整路径第1行元素，计算式为

w0=min {C(1,1),C(1，2)，…,C(1,m)}

(8)

动态时间规整算法对规整路径W做了一定限制，只有满足下面3个条件才可成立。

(1)边界约束

(9)

任何2个序列都有可能变化，但其各部分的先后次序不会改变，因此所选路径必定是从网格左下角出发，在右上角结束。

(2)连续性约束

对路径中wk-1=(n′,m′)和wk=(n,m) 2点，需满足连续性约束条件

(10)

式(10)表明在计算路径时不可能跨过某个点去匹配，只能和相邻点对齐。这可以保证测试样本和模板样本中每个坐标都出现在W中。

(3)单调性约束

对路径中wk-1=(n′,m′)和wk=(n,m) 2点，要求

(11)

式(11)限制了W上面的点必须要随时间单调进行。由式(10)、(11)可知，对于任意一个网格点(n,m)，下一个通过的网格点只可能是(n,m-1)、(n-1,m-1)和(n-1,m)。最小规整成本路径求解过程如图4所示。

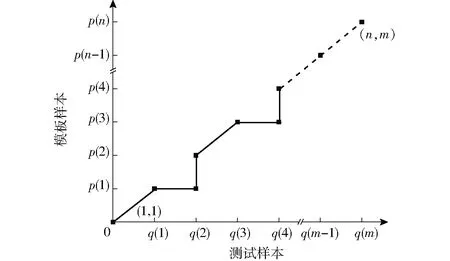
图4 最小规整路径Fig.4 Minimum warping path

通过计算最小规整路径从连续的步态序列中分割单个步幅。路径W的起点和终点分别代表步幅的起点和终点，每个分割点的累积成本必须小于分割阈值，因此，选取合适的分割阈值对步态进行分割。

3 跛行识别模型建立

3.1 步态特征提取

对于每个分割的步幅分别提取统计学和运动学步态特征参数，包括均值A[20]、方差[20]、合加速度Ml[20]、运动变化量Mv[20]、信号幅度面积Sma[21]、平均强度Al[21]、偏度Sk[22]、峰度Fk[22]、步态周期Ts、步幅数Fs、支持时间St和步幅长度Ls。步幅数为连续序列中分割的步幅数量，支撑时间通过前进加速度数据变化率计算，步态周期为步幅分割点之间的时间差，而步幅长度由步行总距离除去步幅数得出。

由于健康奶牛和跛行奶牛样本数量不一致，且可能存在非正态分布，因此采用Wilcoxon秩和检验对提取的特征进行分析，确定跛行奶牛与健康奶牛特征参数间关系。

3.2 跛行识别模型

目前，国内跛行识别研究主要集中在基于计算机视觉和压力板测量方法上[23-25]，国外主要通过基于各种传感器及压敏垫方法采集数据进行跛行识别的研究[26-30]。本文利用逻辑回归法建立奶牛跛行识别模型[31]，根据统计检验结果选取与跛行相关的6个步态特征参数，建立单因素逻辑回归模型。将轻度、中度和严重度跛行合并为一个类别，称之为“跛行”。以二分类变量为模型输出，“1”表示跛行，“0”表示健康。

对于二分类问题可设置一个阈值，如果G(x)≥0.5，则预测y=1，即该奶牛患有跛行。如果G(x)≤0.5，则预测y=0，即该奶牛为健康。为预测输出类似于概率一样介于0～1之间，将sigmoid函数作为映射函数得到逻辑回归模型,计算公式为

(12)

式中xi——步态特征值

α——回归截距β——回归系数

G——跛行发生概率

yi——观测值标签i——样本序号

逻辑回归是非线性模型，利用最大似然估计法对模型系数进行估计。设Gi=G(yi=1|xi)为给定xi条件下得到的跛行yi=1概率，而yi=0的条件概率为G(yi=0|xi)=1-Gi。因此，逻辑回归模型的似然函数计算公式为

(13)

对式(13)两边取对数，得到逻辑回归对数似然函数，并利用极大似然估计法求最佳回归系数。

4 结果与分析

4.1 步态分割结果对比

本文共采集30头奶牛976个样本数据，其中健康奶牛(得分1)21头共613个样本、轻度跛行(得分2)奶牛2头共102个样本、中度跛行(得分3)奶牛4头共137个样本、严重跛行(得分大于等于4)奶牛3头共124个样本。从每组生成模板样本，计算每组模板样本与对应测试样本间累积成本矩阵，根据动态规整原则寻找最小规整路径，确定分割起点和终点，最终从连续的步态序列中分割单个步幅。

图5为利用前进方向加速度信号分割的单个步幅，步态周期开始于趾蹄接触地面终止于趾蹄下一次接触地面，图5中红色虚线之间为一个步态周期。在趾蹄接触地面时刻前进方向加速度值反向最大，之后有一个正方向的加速度信号后进入支撑阶段，在支撑阶段趾蹄相对静止，因此前进方向加速度值变化不大，图中黑色虚线之间表示支撑阶段。支撑阶段后进入摆动阶段，摆动阶段开始于趾蹄抬起地面，终止于趾蹄接触地面，趾蹄抬起时刻前进方向加速度值正向最大，图中黑色虚线和红色虚线之间为摆动阶段。通过分析可知，前进方向加速度信号下峰值均出现在每个步态周期开始时刻，因此该信号下峰值对应步幅的起点和终点。

图5 分割的步幅示意图Fig.5 Schematic of segmented stride

步态分割主要以减少步幅丢失和最小化错误分割为目的。本文利用混淆矩阵来对分割结果进行分析，精确度U、灵敏度V、准确率E计算公式为

(14)

(15)

(16)

式中Tp——正确分割为步幅的样本数量

Fp——错误分割为步幅的样本数量

FN——无法识别为步幅的样本数量

TN——无效步幅的样本数量

对30头奶牛改进前后的步态分割结果对比如表1所示。将每个分割的步幅与黄金标准进行比较来验证分割的准确性。

表1 算法改进前分割结果对比Tab.1 Comparison of segmentation results %

由表1结果可知，本文算法的精确度、灵敏度、准确率平均值可提高到89.53%、95.51%、87.49%，比改进前分别提高了5.31、4.48、8.43个百分点。其中，轻度跛行奶牛步态分割灵敏度、准确率提高最为明显，较改进前分别提高7.22、12.75个百分点。而中度跛行奶牛步态分割精确度提高到86.44%，较改进前提高了10.81个百分点。

为进一步验证该算法性能，利用峰值检测法、自相关函数法和本文算法对30头奶牛进行步态分割试验，结果表明，峰值检测法总准确率87.44%，自相关函数法总准确率88.82%，改进算法在步态分割准确率方面有所提高，总体准确率提高到90.57%，相较自相关函数法和峰值检测法分别提高了1.75、3.13个百分点。

4.2 步态特征提取结果

为研究健康奶牛和跛行奶牛特征参数间关系，从分割的每个步幅提取步态特征参数，并取均值。利用Wilcoxon秩和检验分析各特征值，结果如表2所示，表中特征值用差异性高到低依次进行排列。分析可知，信号幅度面积、平均强度、步态周期、步幅长度、支撑时间、前进方向加速度均值、运动变化量和方差在健康奶牛和跛行奶牛之间均表现显著性差异(P<0.05)。而峰度和偏度在2个方向上均不存在显著性差异。

表2 Wilcoxon秩和检验分析结果Tab.2 Analysis results of Wilcoxon rank sum test

4.3 跛行预测模型的测试

根据统计学分析结果，选取支撑时间、步幅长度、平均强度、信号幅度面积、前进方向加速度均值和运动变化量等6个特征，利用逻辑回归法建立单因素回归模型。模型输入为特征值，输出为二分类结果，其中“1”表示跛行，“0”表示健康，以0.5作为模型分类阈值。将样本数据的70%作为训练集来获得最佳回归系数，30%作为测试集进行识别模型验证，通过极大似然估计法分别求出各模型回归系数，确定逻辑回归方程。

利用接受者操作特征曲线(Receiver operating characteristic curve，ROC)下的面积[32]评估各预测模型，该面积范围在0～1之间，值越大表明识别率越高，各预测模型识别率与ROC曲线下的面积见表3。结果可知，单因素逻辑回归模型中以前进方向加速度均值为自变量的模型获得较高的识别准确率，为89.45%，ROC曲线下的面积为0.902。其他5个单因素回归模型识别率均不小于81.72%，ROC曲线下的面积均不小于0.804。