利用“思考题”，培养学生的数学品格

吴魁

【摘  要】  现代教学理念越来越重视对于学生独立思考能力的培养，关注学生学习品格的形成。在数学教学中，教师应当利用什么方法来提高学生独立思考的能力呢？又该如何培养学生的数学品格呢？本文将基于此来进行探讨，以思考题的角度谈如何培养学生的数学品格。

【关键词】  思考题;数学品格

现代教育理念提倡培养学生独立思考的能力。尤其对于数学教学，教师应当注重培养学生独立思考的能力，形成学生的数学思维，应当利用现代化的教学方式和教学手段不断更新教学体系，以更丰富的形式培养学生的数学品格。

一、培养学生积极的思维态度，为数学品格培养奠基

学生具备乐观积极的心理，就能够以更乐观的心态来对待困难，快速解决困难。尤其在数学这种复杂和需要仔细计算的学科当中，教师应当培养学生积极的心态，以更乐观、更包容的心态来解决数学问题，使其在面对数据庞大和复杂的几何数学问题时，可以保持冷静，仔细观察和思考，发现题目当中所存在的数学原理。保持积极的心态，不仅能够让学生沉着冷静地面对数学问题，还能够让学生在思考数学问题过程当中发现更多有效信息，以更快速更准确的方式解答出数学问题。

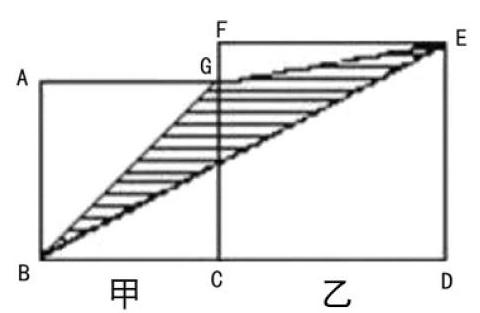
例如，甲、乙两个正方形的边长分别为10厘米、12厘米，求阴影部分的面积是多少。

学生在看到这个的题目时首先就会进行思考，求图中阴影部分三角形的面积，学生的惯性思维就是要去寻找阴影三角形的底和高，而這个特殊的阴影三角形的各边长度条件都没有给出，所以这个三角形是不能够直接以底乘高除2的方式来求面积的。这就需要学生进行仔细思考，如何将求三角形面积转化为其他方式呢？学生在冷静的观察和思考中能够明显发现图中阴影部分三角形的面积就是两个正方形的面积减去三个空白三角形的面积之差。这三个三角形分别是三角形ABG、三角形BDE和三角形EFG。 两个正方形的面积减去三个小三角形的面积之差即为阴影部分三角形的面积。通过面积公式计算得出两个正方形的面积和为224平方厘米，其余三个空白三角形的面积之和为194平方厘米，用正方形的面积和减去三角形的面积和得出阴影部分三角形的面积为50平方厘米。此题解法精妙，通过这种类型的几何思考题能够促进学生对于数学问题的独立思考，让学生发现几何问题中所存在的内在联系是解题的关键。

二、培养学生科学的思考方式，为数学品格培养引路

在实际的教学活动中，教师往往只重视对于教学结果的验收，而忽视了学生的品格成长，导致学生在学习知识的过程中盲目死记硬背，无法掌握科学的学习方法，没能培养出良好的学习习惯。学生在思考数学问题时思维相对混乱，教师应当重视学生科学学习方式的养成，应当充分利用多元表征，让学生进行有序观察，不断提高学生数学素养和动手能力，使学生混乱的学习方式逐渐科学化和体系化，将学生记忆中的碎片化知识点进行整合，使学生所学到的数学知识更加系统化、有序化，不断培养学生的逻辑思维能力，让学生掌握正确的学习方法。

例如，下图中一共有多少个小正方体？你是怎么数的？

这道题需要学生指出整个立体图形中包含着多少个小正方体。

在通常情况下，学生首先想到的就是进行数数和单面观察，学生先数了第一层有几个，然后再逐层向下数正方体，以此来推出整个立体图形所包含的小正方体个数。这种方法是最为常用的，另一种方法也是许多学生所能够想到的普遍方式，这种方法就是以计算直角的方式将问题转化成计算小正方体的方式。在应用这种方法的过程中，学生需要将直角个数转化为正方体的个数，更加凸显出学生的逻辑推理能力和空间想象力。在这种计算条件之下，学生也能够在很短时间内得出正确答案。然而，并不是所有学生都具备良好的空间想象能力，有些学生缺乏一定的空间想象能力，就会觉得这类几何题目相对复杂，学生在做类似题目时就会忽视被遮住的部分。这道几何空间想象题还有另一种解决方式。首先我们将数露出的部分转化为数出缺少的部分，对我们的思维进行可视化处理，先将整个立体图形补成正方体，再一次从下往上数每一层所减少的小正方体的个数，这样学生的思维进行了转化，能所发现几何问题处理的关键诀窍，从而能够顺利解出这道题目，小正方体的个数为：64-1-4-9，最终的答案为50个。在数学教学活动当中，教师在讲解此类题目时通常都会进行简略讲解，因为并不是每一个学生都能够充分理解。教师通常都急于将最简单最容易理解的方法教给学生，强制学生死记硬背单一的解题方法，并没有让学生掌握科学的学习方式。在教学中，教师不应该成为主体，应当作为补充的角色，让学生成为课堂的主要人物，积极培养学生的思考能力和想象力及创新能力，让学生在思考和创新过程当中提高对于数学题目的理解，以多种类型的思考题来提升学生的数学品格。当学生出现失误和错误时，教师应当进行积极引导，不能过度批评，以免挫败学生的学习积极性。

三、培养学生思维的批判性和创造性，为数学品格培养护航

教师在培养学生数学品格的过程中应当关注学生的批判性思维和创造性思维培养，积极鼓励学生以多种不同的方法来解决题目，鼓励学生驳斥传统解题思路，鼓励学生运用自身所具备的数学能力和解题方法来创造属于自己和适合自己的解题方法，不断提高学生的批判性思维和创造性思维，提升学生的整体数学能力。

在小学课本当中，鸡兔同笼问题是一道经典的例题。例如，笼中有头36个，有脚120只，求鸡和兔各有多少只？对鸡兔同笼问题，有些对数学不敏感的学生就会感到难以解答，认为鸡兔同笼是十分复杂的问题。其实，对于鸡兔同笼问题的解答，思路很多：可以假设此时笼子里全是鸡或者假设此时笼子里全是兔。通过计算能够得出此条件下有24只兔和12只鸡。小学课本当中的稀释问题也很经典，如：有20千克浓度15%的糖水，问需要加多少千克的水才能够将糖水的浓度变为10%。首先应求出在20千克的糖水当中含糖的质量，20×15%=3（千克）。原本糖的质量为3千克，水的质量为20-3=17（千克）。那么学生就要进行思考，要加入多少水之后才能够将糖水的浓度降到为10%呢？3÷10%=30（千克）。最后，用30-20=10（千克）得出应该加水10千克的结论。

小学生思考题的数量众多、种类丰富，利用思考题可以激发学生的数学学习兴趣，提升学生的数学品格。此外，教师在培养学生数学品格的过程当中，还需要不断提升学生的数学素养，激发其数学学习兴趣。

【参考文献】

[1]雷淑蓓.加强数学思想方法教学 提高学生数学素质品格[J].广西教育学院学报，1998（S1）：168-171.

[2]梁小茹.以“五学”课堂教学模式提升小学生数学核心素养[J].新课程研究，2019（10）：46-47.