一种改进的核可能性C?均值聚类图像分割算法
2020-07-23梁丹于海燕范九伦雒僖
梁丹 于海燕 范九伦 雒僖


摘 要: 可能性C?均值聚类(PCM)算法比传统模糊C?均值聚类算法具有更好的鲁棒性,但其应用于图像分割时没有充分考虑图像的局部空间信息。基于PCM算法,提出一种核空间与自适应中值滤波相结合的改进算法。算法利用自适应中值滤波获得像素的局部空间信息,并由此生成一种新的模糊因子加入到目标函数中,然后在核空间中对目标函数进行优化求解,得到最优聚类中心和隶属度。由实验结果可知,所提算法对被高椒盐噪声污染的图像具有较高的准确性和鲁棒性。
关键词: 可能性C?均值聚类; 目标函数求解; 自适应中值滤波; 局部空间信息; 图像分割; 实验分析
中图分类号: TN911.73?34; TP391 文獻标识码: A 文章编号: 1004?373X(2020)05?0046?05
An improved kernel possibilistic C?means clustering algorithm for image segmentation
LIANG Dan1, 2, 3, YU Haiyan1, 2, 3, FAN Jiulun1, 2, 3, LUO Xi1, 2, 3
(1. School of Communication and Information Engineering, Xian University Posts and Telecommunications, Xian 710121, China;
2. Key Laboratory of Electronic Information Application Technology for Investigation, Ministry of Public Security, Xian 710121, China;
3. Shaanxi International Joint Research Center for Wireless Communication and Information Processing, Xian 710121, China)
Abstract: The possibilistic C?means (PCM) clustering algorithm has better robustness than traditional fuzzy C?means clustering algorithm, but it fails to fully consider the local spatial information of image when it is applied to image segmentation. In view of this, an improved algorithm combining kernel space and adaptive median filtering is proposed based on the PCM algorithm. In the algorithm, the adaptive median filtering is used to obtain the local spatial information of pixel, with which a new fuzzy factor is generated and added to an objective function, and then, the objective function is optimized and solved in the kernel space to obtain the optimal cluster center and the membership degree. The experimental results show that the proposed algorithm has high accuracy and robustness for images contaminated by high salt?and?pepper noise.
Keywords: possibilistic C?means clustering; objective function solution; adaptive median filtering; local spatial information; image segmentation; experiment analysis
0 引 言
图像分割是图像处理领域中一项重要的研究内容,它将图像分为不同的区域,这些区域具有相同的特点,如灰度级、颜色、色调、纹理等。图像分割技术在目标识别与跟踪、图像检索以及人脸识别等领域具有重要价值。模糊聚类算法在图像分割[1?6]中应用最为广泛,其中,模糊C?均值聚类(FCM)算法[7?8]在图像分割中应用最流行,它是一个著名的非监督模糊聚类算法。FCM算法存在对噪声敏感的缺点,因为有约束条件隶属度值归一化的限制,使得数据点中噪声点和非噪声点对聚类具有相同的影响力,导致噪声点具有较大的隶属度而被划分到某一类中。为此,学者们在FCM算法的基础上对隶属度提出了很多改进算法[9?12],其中,可能性C?均值聚类(PCM)算法[13]放弃了对隶属度归一化的限制,使得噪声数据具有较小的隶属度值,提高了算法的鲁棒性。FCM算法和PCM算法主要适合对团状凸数据聚类,对那些非凸数据聚类时,其聚类性能并不理想,为此文献[14?15]提出了基于核空间的模糊C?均值聚类(KFCM)算法和基于核的可能性聚类(KPCM)算法,它通过核函数将样本数据通过非线性映射至高维特征空间,对非凸数据也能够取得较理想的聚类结果,改善了样本的可分性,提高了算法的聚类性能。
然而,当图像中含有大量噪声时,PCM算法无法得到理想的分割效果,因为它忽略了图像的空间位置信息。目前学者们已经在传统的FCM算法中加入空间信息[16?18],提出了大量基于FCM算法的改进算法,改善了图像的分割结果。但由于FCM算法对噪声敏感,因此改进算法也存在对噪声敏感的缺点。PCM算法在一定程度上对噪声具有鲁棒性,结合空间信息的PCM算法能够进一步提高图像的分割结果。
针对被高椒盐噪声污染的图像,利用自适应中值滤波算法能够根据噪声大小自适应调节滤波半径的特点,本文提出一种改进的核可能性C?均值聚类图像分割算法,提高了算法的聚类性能和有效性,进一步解决了在强噪声干扰下图像的聚类分割效果不理想的问题。仿真实验结果表明了本文算法的有效性。
1 可能性C?均值聚类算法
设数据集[X]由[n]个[p]维的数据组成,数据集可表示为[X={x1,x2,…,xn}∈Rn×p],可能性C?均值聚类算法是一种迭代聚类方法,通过最小化目标函数对样本数据进行分类,其目标函数[Jm]可表示为:
[Jm(T,V)=i=1nk=1ctmkixi-vk2+k=1cηki=1n(1-tki)m] (1)
满足约束条件:
[i=1ntki>0,k=1,2,…,c, 0≤tki≤1] (2)
式中:[n]表示数据样本的个数;[c]表示聚类个数;[m]表示模糊加权指数,常取[m=2];[T=[tik]]([i=1,2,…,n];[k=1,2,…,c])为隶属度矩阵,表示第[i]个样本对第[k]个聚类中心的隶属程度;[V=[vk]]([k=1,2,…,c])表示聚类中心集合;[ηk]为一正数,一般取值为:
[ηk=Ki=1ntmkixi-vk2i=1ntmki] (3)
式中[K]为一正整数,通常取[K]=1。
隶属度[tki]和聚类中心[vk]的迭代公式为:
[tki=1+xi-vk2ηk-1m-1] (4)
[vk=i=1ntmkixii=1ntmki] (5)
通过反复迭代式(4)~式(5),使得PCM算法收敛。
2 图像分割算法
2.1 自适应中值滤波算法
自适应中值滤波算法[19]主要有三个目的:去除脉冲噪声;平滑其他非脉冲噪声;保护图像边缘信息。它在滤波时使用一个矩形区域的窗口[Sxy],能够根据噪声强弱改变滤波窗半径的大小。当判断滤波窗中心像素是噪声时,自适应中值滤波器为常规中值滤波器,即用中值代替该值;当判断滤波窗中心像素不是噪声时,则不改变其当前像素值。自适应中值滤波器能够得到比常规中值滤波器更好的滤波效果,因为它对噪声概率更大的脉冲噪声进行平滑的同时还能更好地保持图像细节。
自适应中值滤波算法由两部分组成:第一层(Leve1A)和第二层(Leve1B)。
第一层(Leve1A):
[A1=Zmed-Zmin] (6)
[A2=Zmed-Zmax] (7)
如果[A1]>0并且[A2]<0,则转到Leve1B,否则增加滤波窗[Sxy]的尺寸。如果滤波窗[Sxy]的大小达到[Smax],则重复执行Leve1A,否则把[Sxy]作为输出。
第二层(Leve1B):
[B1=Zxy-Zmin] (8)
[B2=Zxy-Zmax] (9)
如果[B1]>0并且[B2]<0,则把[Zxy]作为输出值,否则把[Zmed]作为输出值。
式中:[Zmin]表示在[Sxy]滤波窗内灰度的最小值;[Zmax]表示在滤波窗[Sxy]内灰度的最大值;[Zmed]表示在[Sxy]滤波窗内灰度的中值;[Zxy]表示坐标[(x,y)]处的灰度值;[Smax]表示[Sxy]所允许的最大窗口尺寸。
2.2 一种改进的核可能性C?均值聚类图像分割算法
FLICM[17]算法在目标函数中引入无参数模糊因子[Gki],即引入局部空间信息,控制图像中噪声和细节的平衡,但是对受高强度噪声污染的图像无法达到理想分割的效果。在本文算法中,用核空间欧氏距离代替PCM中样本与聚类中心之间的欧氏距离,引入自适应中值滤波算法对图像进行滤波,并将模糊因子中的局部邻域值替换为自适应中值滤波的像素值,以更好地利用邻域像素。
新的目标函数为:
[Jm=i=1nk=1ctmkiΦ(xi)-Φ(vk)2+G′ki+ηk=1ci=1n(1-tki)m] (10)
满足约束条件:
[i=1ntki>0, k=1,2,…,c; 0≤tki≤1] (11)
式中:[n]表示一幅图像的像素个数;[c]表示图像的聚类数目;[tki]表示第[i]个像素对[k]个聚类中心的隶属度值;参数[m]表示隶属度的加权指数,决定聚类结果的模糊程度,[m∈1,+∞],通常[m]=2;[xi]表示原始图像的像素;[vk]表示聚类中心;[Φ]表示高维空间的非线性映射;[G′ki]表示模糊因子;[η]为一正数。
其中,调整模糊因子为:
[G′ki=j∈Nii≠j11+dij(1-tkj)mΦ(xj)-Φ(vk)2] (12)
式中:[xj]表示经过自适应中值滤波后的像素;[Ni]表示中心像素为[i]的邻域窗口;[dij]表示中心像素[i]和其所对应邻域窗口中的像素[j]之间的欧氏距离;[tkj]表示隶属度。
核空间平方欧氏距离为:
[Φ(xi)-Φ(vk)2=K(xi,xi)+K(vk,vk)-2K(xi,vk)] (13)
当取高斯核函数时,[K(x,x)=1,K(x,y)=exp-x-y2σ2],则:
[Φ(xi)-Φ(vk)2=21-K(xi,vk)] (14)
式中[σ]表示带宽,表示为:
[σ=1N-1i=1N(di-d)12] (15)
式中:[d]表示像素[xi]和像素均值[x]之间的距离,[d=xi-x],[d]的表达式为:
[d=i=1NdiN] (16)
将高斯核函数公式代入目标函数,可将目标函数简化为:
[Jm(T,V)=i=1nk=1ctmki1-K(xi,vk)+G′ki+k=1cηi=1n(1-tki)m] (17)
式中:
[G′ki=j∈Nii≠j11+dij(1-tkj)m(1-K(xj,vk))] (18)
隶属度[tki]和聚类中心[vk]的表达式为:
[tki=1+2(1-K(xi,vk))+G′kiη-1m-1] (19)
[vk=i=1ntmki(K(xi,vk))xi+A1i=1ntmki(K(xi,vk))+A2] (20)
式中:
[A1=i=1ntmkij∈Nii≠j(1-tkj)m(K(xj,vk))xj11+dij] (21)
[A2=i=1ntmkij∈Nii≠j(1-tkj)m(K(xj,vk))11+dij] (22)
本文算法步骤为:
Step1:设置聚类类别数[c],隶属度加权指数[m],迭代误差限[ε],最大迭代次数[T],初始迭代次数[t]=1。
Step2:通过自适应中值滤波算法对图像进行平滑处理,得到滤波后的图像[I1]。
Step3:运行FCM算法,把FCM得到的隶属度划分矩阵作为本文算法的初始隶属度矩阵[t(0)ki]。
Step4:通过式(20),更新聚类中心[v(t)k]。
Step5:通过式(21),更新隶属度[t(t)ki]。
Step6:当[v(t)k-v(t+1)k<ε]或者[T>Tmax]时停止迭代,输出隶属度[t(t)ki]和聚类中心[v(t)k];否则,返回Step4进行下一次迭代。
Step7:通过对最终输出的隶属度[t(t)ki]和聚类中心[v(t)k]产生分割图像[I2]。
3 实验结果及分析
通过Matlab仿真软件来验证本文算法对人工合成图像和自然图像的有效性及鲁棒性,并用PCM[13],KFCM_S1[16],KFCM_S2[16],ARKFCM[18],FLICM[17]算法作為比较算法。对所有的比较算法,设置共同参数为[m=2],[ε=]0.000 01,局部邻域窗口为3×3。对于KFCM_S1和KFCM_S2算法,取[a=2]。对于本文算法,设置自适应中值滤波的最大滤波半径为10,[η=]0.05。
实验一:对人工图像(synthetical,200×200)添加强度为0.2的椒盐噪声,采用6种算法对其进行分割,分割结果如图1所示。
从图1中可以看出,PCM算法的分割结果最不理想,其中包含的噪声点最多,这是因为PCM算法忽略了图像中像素的空间信息,导致算法对噪声敏感。KFCM_S1算法、KFCM_S2算法引入了均值滤波和中值滤波,结合了图像像素的空间信息,并转化到核空间。相比而言,对于含椒盐噪声的图像,KFCM_S2比KFCM_S1的分割效果更好,但分割结果中仍含有噪声,分割效果欠佳。ARKFCM引入正则化参数控制空间信息,同样转化到核空间,但对被噪声影响严重的图像分割效果较差。FLICM算法结合了图像局部信息的灰度信息和空间信息,能够更多地利用图像中像素的空间信息,但是仍对含噪强度较大的图像鲁棒性较差,因此该算法的分割效果仍然不理想。本文算法通过引入自适应中值滤波,并结合滤波后图像像素的局部空间信息,同时使用具有鲁棒性的核函数,因此得到了理想的分割效果。
采用分割精度[17](Segmentation Accuracy,SA)作为算法性能的客观评价指标,可表示为:
[SA=i=1cAi?Cij=1cCj] (23)
式中:[c]表示聚类个数;[Ai]表示由分割算法得到属于第[i]类的像素点集;[Ci]表示在标准图像中属于第[i]类的点集;SA表示正确分类的像素数占图像像素总数的比重。
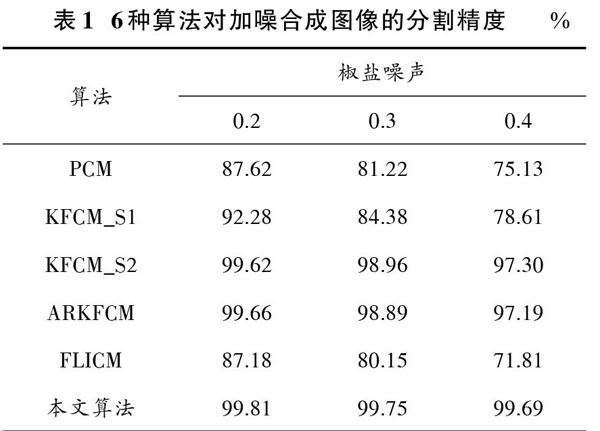
表1给出了随着噪声强度增强,6种不同算法分割结果的分割精度(SA)值。由表1可得,随着噪声强度的增大,其余5种算法分割精度逐步降低,但本文算法仍然能够保持较高的分割精度。
实验二: 图像(#42049 321×481)添加强度为0.1的椒盐噪声和均值为0,方差为0.001的高斯噪声,使用6种算法分别对其进行分割,结果如图2所示。
由图2可以看出,PCM,KFCM_S1,KFCM_S2,ARKFCM和FLICM算法的分割结果中均含有不同程度大小的噪声,对噪声的抑制能力不强,算法的鲁棒性较差,因此这5种算法对图像#42049的分割效果不佳。而本文算法对噪声有一定的抑制能力,具有更好的鲁棒性,得到了较好的分割效果。
表2为对图像#42049分别添加不同噪声强度的混合噪声,Mixed1,Mixed2,Mixed3分别表示均值为0,方差为0.001和强度为0.1,0.2,0.3的椒盐噪声,并采用峰值信噪比[20](Peak Signal?to?Noise Ratio,PSNR)作为客观评价指标。由表2可得,随着噪声强度的增大,本文算法相比于其他5种算法具有较高的峰值信噪比,进一步证明了本文算法的鲁棒性。
实验三:图像cameraman(256×256)添加强度为0.2的椒盐噪声,使用6种算法分别对其进行分割,结果如图3所示。
由图3和表3可明显看出,将本文算法与PCM,KFCM_S1,KFCM_S2,FLICM,ARKFCM算法作比较,可明显得出本文算法具有较好的分割结果,且随着噪声强度的增大,本文算法仍能够保持较高的鲁棒性。
4 结 语
本文提出一种改进的核可能性均值聚类图像分割算法。算法通过利用模糊因子和自适应中值滤波获取图像的局部空间信息,并采用核空间欧氏距离代替传统的欧氏距离作为相似性度量,最后实现对加入椒盐噪声图像的分割。通过仿真实验表明,本文算法相比于PCM,KFCM_S1,KFCM_S2,FLICM,ARKFCM算法具有更好的分割效果和鲁棒性。
参考文献
[1] BAI X, CHEN Z, ZHANG Y, et al. Infrared ship target segmentation based on spatial information improved FCM [J]. IEEE transactions on cybernetics, 2016, 46(12): 3259?3271.
[2] WAN L, ZHANG T, XIANG Y, et al. A robust fuzzy C?means algorithm based on Bayesian nonlocal spatial information for SAR image segmentation [J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2018, 11(3): 896?906.
[3] NGATCHOU A, BITJOKA L, MFOUMOU E, et al. Robust and fast segmentation based on fuzzy clustering combined with unsupervised histogram analysis [J]. IEEE intelligent systems, 2017, 32(5): 6?13.
[4] DESPOTOVIC I, VANSTEENKISTE E, PHILIPS W. Spatially coherent fuzzy clustering for accurate and noise?robust image segmentation [J]. IEEE signal processing letters, 2013, 20(4): 295?298.
[5] CAO H, DENG H, WANG Y. Segmentation of M?FISH images for improved classification of chromosomes with an adaptive fuzzy C?means clustering algorithm [J]. IEEE transactions on fuzzy systems, 2012, 20(1): 1?8.
[6] MAT ISA N A, SALAMAH S A, NGAH U K. Adaptive fuzzy moving K?means clustering algorithm for image segmentation [J]. IEEE transactions on consumer electronics, 2009, 55(4): 2145?2153.
[7] BEZDEK J C. Pattern recognition with fuzzy objective function algorithms [M]. New York: Plenum Press, 1981.
[8] LIU G, ZHANG Y, WANG A. Incorporating adaptive local information into fuzzy clustering for image segmentation [J]. IEEE transactions on image processing, 2015, 24(11): 3990?4000.
[9] ZHU L, CHUNG F, WANG S. Generalized fuzzy C?means clustering algorithm with improved fuzzy partitions [J]. IEEE transactions on systems, man, and cybernetics, Part B (Cybernetics), 2009, 39(3): 578?591.
[10] 文传军,詹永照.基于样本模糊隶属度归[n]化约束的松弛模糊C均值聚类算法[J].科学技术与工程,2017,17(36):96?104.
[11] 胡嘉骏,侯丽丽,王志刚,等.基于模糊C均值隶属度约束的图像分割算法[J].计算机应用,2016,36(z1):126?129.
[12] GHARIEB R R, GENDY G, ABDELFATTAH A, et al. Adaptive local data and membership based KL divergence incorporating C?means algorithm for fuzzy image segmentation [J]. Applied soft computing, 2017, 59: 143?152.
[13] KRISHNAPURAM R, KELLER J M. A possibilistic approach to clustering [J]. IEEE transactions on fuzzy systems, 1993, 1(2): 98?110.
[14] ZHANG D Q, CHEN S C. A novel kernelized fuzzy C?means algorithm with application in medical image segmentation [J]. Artificial intelligence in medicine, 2004, 34(4): 1907?1916.
[15] 吕佳,熊忠阳.基于核的可能性聚类算法[J].计算机工程与设计,2006,27(13):2466?2468.
[16] CHEN S C, ZHANG D Q. Robust image segmentation using FCM with spatial constraints based on new kernel?induced distance measure [J]. IEEE transactions on systems, man, and cybernetics, Part B (Cybernetics), 2004, 34(4): 1907?1916.
[17] KRINIDIS S, CHATZIS V. A robust fuzzy local information C?means clustering algorithm [J]. IEEE transactions on image processing, 2010, 19(5): 1328?1337.
[18] FANG R, LU Y N, LIU X N, et al. Segmentation of brain MR images using an adaptively regularized kernel FCM algorithm with spatial constraints [C]// 2017 10th International Congress on Image and Signal Processing, Biomedical Engineering and Informatics (CISP?BMEI). Shanghai, China: IEEE, 2017: 1?6.
[19] 冈萨雷斯.数字图像处理[M].阮秋琦,阮宇智,译.北京:电子工业出版社,2006.
[20] 何晶,吴成茂.核空间自适应非局部均值鲁棒分割算法[J].光电子?激光,2017,28(8):910?917.
