浅析弹性力学平面问题的基本解法

杨艳 王章星

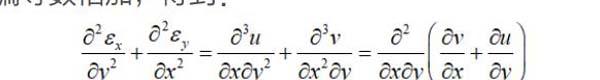
【摘要】本文简单介绍了弹性力学平面问题的两种基本解法以及各种解法的适用范围和优缺点。

【关键词】平面问题;应力;应变;位移;边界

弹性力学通常也被称为弹性理论，主要是对应力、变力以及位移这三个基本的未知函数进行研究，这几个函数都是空间变量，在弹性力学中涉及到的平面问题是指当这三类基本未知函数与某一个坐标轴无关时对应的力学问题。平面问题是二维的问题，它可以非常直观的对弹性力学中的基本理论进行阐述，并且当前在工程中对其计算结果的使用非常广泛，一般被当作弹性力学学习过程中的典型问题以及入门的教学内容来使用，因此弹性力学的基本内容中就包含了对平面问题的求解。对弹性力学的平面问题进行求解，也就是对3个应力分量、3变力分量以及两个位移分量来进行求解，要求这8个未知函数必须能够满足该区域中的基本方程式，同时也要满足边界上面的位移与应力的边界条件。为了能够更好的求解，一般会使用与代数方程中消元法相似的方式进行求解。并且会以选取的基本未知函数的不同为依据，将求解方法分成位移解法与应力解法两种。在很多实际的工程问题中，体力是常量，此时则可以采用应力函数法求解平面问题。

1、位移解法

位移解法指的是按照位移来进行求解的方法，与结构力学中包含的位移法相近。不管是平面应力问题还是应变问题，对平衡微分方程与几何方程的方法都是相同的，平面问题中涉及大的平衡微分方式如下：

平面问题的几何方程为

在平面应力问题中，物理方程为

在平面应变问题中，物理方程为

从上面我们能够看得出来，平面的应力问题与应变问题所涉及的物理方程是不同的，所以把平面应力问题中的E转换为       ，v转换为    ，平面应变问题的物理方程就能够得出来。接下来将使用平面的应力问题当作例子，应用位移解法来对平面问题求解。

首先选取基本未知函数为位移分量u和v。

因为几何方程本身就是使用位移分量来表示应变分量的表达式，所以我们可以只将物理方程中的应变分量为依据对应力分量进行表示，然后再把几何方程式代入其中，然后就能够得到使用位移分量来表示的应力分量表达式：

在平面问题涉及到的平衡微分方程中把使用位移分量来表示的应力分量的表达式代入，可以得到一个使用位移分量来表示的平衡微分方程，也就是位移解法中的基本微分方程：

在应力的边界条件中把使用位移分量来表示的应力分量表达式代入，从而求出平面问题的位移解法的应力边界条件为：

除此之外，位移分量还需满足位移边界条件

总结来说，使用位移解法来对平面应力问题进行求解，其实就是使得位移的分量u和v在指定的区域内可以满足该解法的基本微分方程，以及能够在边界上满足其应力的边界条件和位移的边界条件。

对平面上的应变问题而言，把平面应力问题中的E转换为      ，v转换为      ，我们就可以得到平面应变问题的位移解法的基本微分方程以及其应力的边界条件，并且位移的边界条件不会改变。

2、应力解法

应力解法指的是使用应力的方式进行求解，与结构力学中的力法相似。

在应力解法中其基本未知函数是应力分量。位移分量和应变分量从基本方程和边界条件中消除。基本微分方程和相应的边界条件由应力分量表示。由此求出应力分量，然后计算求得应变分量和位移分量。

首先选取应力分量σx，σy及τxy为基本未知函数。

物理方程就是使用应力分量来对应变分量来进行表示。为了使得位移分量可以用应力分量表示出来，应该把物理方程代入到几何方程中，再利用函数积分来求出位移分量。应力分量的位移表达式也会比较繁琐，并且包含着待定的积分项。又由于应力分量表达式也很复杂，求解非常困难。因此当使用应力法对弹性力学平面问题进行求解时，一般支队全部是应力边界条件的问题进行求解，假设所有的边界都是应力边界条件，那么：

因为平衡微分方程本身是由应力分量表示的，因此可以作为求解应力分量的基本微分方程

我们可以从上面的平衡微分方程看出来，两个方程是无法对3个应力变量进行求解的，所以应该在几何方程与物理方程中把位移分量与应变分量消除掉，把只含有应力分量的补充方程导出来，这个方程就是应力协调方程。

因为在基本方程当中只有几何方程是存在位移分量的，所以可以在几何方程中先将位移分量消掉。将 对 的二阶偏导数和 对 的二阶偏導数相加，得到：

将上式化简可以得出

为了进一步简化应力协调方程，使其只包含正应力而不包含切应力，可以将平衡微分方程改写为

将以上两个式子分别对x和y求偏导数，相加得到

代入到应力协调方程，得到简化后的平面应力问题的应力协调方程

针对平面应变问题，把平面应力问题中的E转换为       ，v转换为       ，便可得到平面应变问题的应力协调方程。

总结来说，在所有的边界条件都是应力边界条件时，能够使用应力解法对平面问题进行求解，而且所得到的应力分量都应该满足区域内部的平衡微分方程式以及应力协调方程式，同时还要满足边界上面的应力边界条件。对单连体来说，只要能够满足前面所说的条件的应力解答，那么该解答就是合理的解在实际的问题中。而对应多连体来说，还应当满足多连体位移所需的单值条件。

结语：

弹性力学的平面问题求解的基本方法主要有两种，分别是位移解法以及应力解法，这两种方法同时也是在学习弹性力学平面问题过程中必须要掌握的基础方法。对于位移解法，求解位移函数往往会遇到很大的困难，因为需要从较复杂的微分方程式和边界条件式等具体求解，因此能得到的位移函数解答较少。尽管如此，位移解法仍然是弹性力学问题的一种基本解法，它可以适应很多种边界条件问题的求解，在对弹性力学的非常多种的近似数值求解种应用的特别多。

参考文献：

[1]徐芝纶.弹性力学简明教程[M].4版.北京：高等教育出版社，2013.

[2]吴家龙.弹性力学 [M].4版.北京：高等教育出版社，2011.

[3]刘章军.弹性力学内容简要与典型题解[M].北京：中国水利水电出版社，2009.