基于模糊PID算法的双闭环直流调速系统中的设计

朱嵘涛 陈希湘

摘  要： 设计一种基于模糊PID算法的双闭环直流调速系统，其主要由三相对称交流电压源、晶闸管整流桥、同步6脉冲触发器、转速调节器、电流调节器和直流电机等组成。系统以模糊PID算法为控制核心，由同步6脉冲触发器产生脉冲来实现对直流电机的速度调节。目标转速值确定后，通过仿真对比传统工程整定法和模糊PID算法，结果表明，两种方法都实现了对电机转速的控制，但模糊PID算法的转速曲线更平滑、调节时间更短、超调更小，能满足工控领域要求。

关键词： 双闭环直流调速; 系统设计; 系统组成; 模糊PID算法; 模块建模; 仿真测试

中图分类号： TN722.7+2?34; TP242               文献标识码： A                     文章编号： 1004?373X（2020）14?0034?04

Design of double closed?loop DC speed governing system based on fuzzy PID algorithm

ZHU Rongtao， CHEN Xixiang

（Yangtze University College of Technology & Engineering， Jingzhou 434020， China）

Abstract： A double closed?loop DC speed governing system based on fuzzy PID algorithm is designed. The system is composed of three?phase symmetrical AC voltage sources， thyristor rectifier bridge， synchronous 6?pulse trigger， speed governor， current regulator and DC motor. In the system， the fuzzy PID algorithm is taken as the control core， and synchronous 6?pulse trigger is used to produce pulses to realize the speed governing of DC motor. After the target rpm value is determined， the simulation comparison between the traditional engineering tuning method and the fuzzy PID method is carried out. The results show that both methods can control the motor speed， but the fuzzy PID algorithm rotational speed curve is smoother， its adjustment time is shorter and its overshoot is smaller， which can meet the requirements of industrial control field.

Keywords： close?loop DC speed governing; system design; system composition; fuzzy PID algorithm; module modeling; simulation testing

在工业生产和制造过程中，电机转速是一个非常重要的参数，因此对实现电机转速的精确控制显得非常重要。直流电机转速受到转动惯量、转矩、电压、励磁磁通等诸多因素影响，其转速稳定是一个非稳态过程。模糊PID算法克服了传统PID算法无法实时调整PID参数的缺点，且无需建立复杂的数学模型和控制效果好等优点已广泛应用在工业生产中。该系统以模糊PID算法作为控制中心，通过不断改变导通角来实现电机转速的调节，在提高系统精度的同时也使电机转速得到有效控制。

1  系统整体设计

双闭环直流电机调速系统主要由三相对称交流电压源、晶闸管整流桥、同步6脉冲触发器、转速调节器、电流调节器和直流电动机等组成，系统整体框图如图1所示。

2  经典PID算法

按偏差的比例、积分和微分进行控制的算法简称为PID（Proportional?Integral?Differential）算法。

模拟PID算法的表达式为[1?2]：

[u（t）=KPe（t）+1TI0te（t）dt+TDde（t）d（t）]     （1）

式中：[u（t）]为PID调节器的输出;[e（t）]为PID调节器的偏差，即设定值r（t）与实际测量值y（t）之间的偏差;[KP]，[TI]，[TD]分别为调节器的比例系数、积分系数和微分系数。

模拟PID算法不能直接在Simulink中应用。当采样周期足够小时，通过数值逼近的方法，用求和代替积分，用后向差分代替微分，便可得到数字式PID算法表达式[3]：

[u（k）=KPe（k）+TTIj=0ke（j）+TDe（k）-e（k-1）T]  （2）

在式（2）中，令：

[KI=KPTTI，  KD=KP·TDT]

则PID算法的表达式为：

[u（k） =KPe（k）+KIj=0ke（j）+KDe（k）-e（k-1）]  （3）

3  模糊PID控制及其算法

模糊PID控制器的结构如图2所示，采用模块直接搭建的模糊PID控制器算法会非常繁琐，故采用S函数的方式来构建该模块[4?6]。

在式（3）中，计算[j=0ke（j）]非常繁琐，故引入状态变量[x（k）=j=0ke（j）]，故可推导出状态方程式：

[x（k）=x（k-1）+e（k-1）]          （4）

由模糊逻辑整定PID的表达式，将式（3）改写成：[u（k） =KP（k）e（k）+KI（k）x（k）+                KD（k）e（k）-e（k-1）] （5）

式中，[KP（k）]，[KI（k）]，[KD（k）]的表达式如下：

[KP（k）=KP（k-1）+λPΔKPKI（k）=KI（k-1）+λIΔKIKD（k）=KD（k-1）+λDΔKD]       （6）

式中：[λP]，[λI]，[λD]均为常数;[ΔKP]，[ΔKI]，[ΔKD]的大小由PID模糊逻辑参数表决定。

4  系统主要单元模块建模

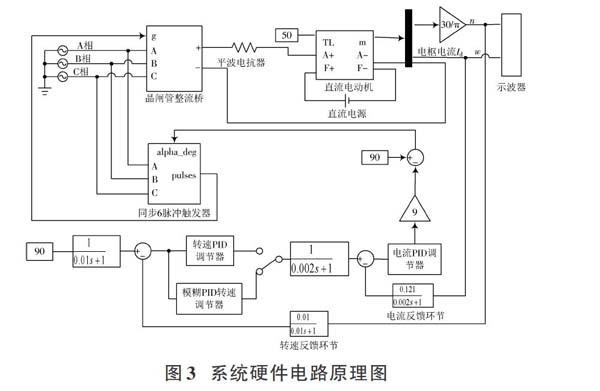
双闭环直流调速系统Simulink仿真图如图3 所示，直流电动机输出的4个信号从上至下分别是：电机角速度、电枢电流、励磁电流和励磁电磁转矩。该系统中只需研究电机角速度和电枢电流，故只将这两个信号引出，电动机输出信号为角速度ω，需将其转化成转速（n=60[ω（2π）]），因此电动机角速度输出端接Gain模块，参数设置为[30π]。额定负载转矩为50。

4.1  同步6脉冲触发器建模

同步6脉冲触发器的建模如图4所示。其中alpha_deg为导通角，输出脉冲由导通角大小来决定，输出脉冲又去控制整流桥的输出电压。

在Matlab中同步6脉冲触发器的输入信号为导通角α，整流桥输出电压Ud0=Ud0（MAX）cos α。当α=0°时，Ud0=Ud0（MAX），此时电机转速达到最大值;当α<90°，整流桥处于整流状态，电机转速由α确定。

4.2  电流PID调节器建模

电流PID调节器建模采用工程整定法，具体计算出的电流调节器的传递函数为：[WACR=KI+1τiS=0.43+58.8231S]。

4.3  转速PID调节器建模

转速PID调节器建模采用工程整定法，计算过程中ASR的传递函数为：[WASR=Kn+1（τnS）=6.02+11.494S]。

4.4  模糊转速PID调节器建模

根据式（5）和式（6），可以写出对应的S函数并封装出对应的模糊控制模块，其内部结构如图5所示。

在模糊PID調节器中，根据经验可以构造出表1、表2和表3，并根据该模糊规则表在Matlab环境下输入模糊推理系统，该系统有2路输入和3路输出。该模型中输入和输出变量的范围均取（-3，3），如表1～表3所示[7?10]。

5  系统仿真测试

文中为了比较模糊PID调节器和转速PID调节器的效果，采用手动开关的形式进行选择。

5.1  转速PID调节器下系统输出测试

在图3所示的Simulink原理图中，首先对传统工程整定法设计的转速PID调节器进行测试，转速设定值为10（其对应的转速为1 000 r/min），将手动开关与转速PID调节器相连，其输出曲线如图6所示。

图6中，在0.347 s转速达到最大值1 204 r/min，在2 s时转速稳定下来，对应转速稳态值为1 007 r/min，其转速最大超调量为19.5%。

5.2  模糊转速PID调节器下系统输出测试

在图3中，转速设定值为10（其对应的转速为1 000 r/min），将手动开关与模糊转速PID调节器相连，其输出曲线如图7所示。

图7中，在0.337 s时转速达到最大值1 029 r/min，在1 s时转速稳定下来，对应转速稳态值为1 005 r/min，其转速最大超调量为2.4%。与图6相比，图7中电机转速超调量更小，且曲线更加平滑。为了更好地对比两种方法下对双闭环直流调速系统的控制效果，引入了转速最大值、转速最大值调节时间、转速稳态值、转速调节时间、最大超调量和残余偏差6个指标，并将各项数据统计后整合在表4中。

从表4中可知，模糊PID算法在这6项指标中都要优于传统的工程整定法。与传统工程整定法相比，转速调节时间缩短了1 s的前提下，转速的稳态值更接近转速设定值，且最大超调量降低了17.1%。因此模糊转速PID调节器的控制效果更好。

6  结  语

本文设计的双闭环直流调速系统，运用模糊PID算法实现对电机速度的调节。测试结果表明，该系统的调节效果比传统的工程整定法更好，转速调节更平滑且超调更小，很适合应用在工控领域。

注：本文通讯作者为陈希湘。

参考文献

[1] 朱嵘涛，武洪涛.基于增量式PID算法的直流电机调速系统[J].仪表技术与传感器，2017，54（7）：121?126.

[2] 贾智，赵岩，张兵，等.基于小波神经网络PID的战车自适应巡航算法[J].兵器装备工程学报，2019，40（3）：161?164.

[3] 邓剑，潘尚峰.基于模糊PID自适应控制的动力卡盘动态扭矩加载研究[J].机床与液压，2019，47（3）：64?67.

[4] 胡改玲，桂亮，权双璐，等.串联模糊PID控制的四旋翼无人机控制系统设计[J].实验技术与管理，2019，36（3）：132?135.

[5] 周克良，过振宇.基于模糊自适应PID的推挤机线径预测控制[J].计算机仿真，2019，36（3）：302?305.

[6] 柴钰，王乔.粒子群优化模糊PID的履带机器人运动控制研究[J].现代电子技术，2018，41（18）：49?52.

[7] 郭志强，余红英，刘摇琛.基于模糊PID的高速振镜电机控制[J].微特电机，2019，47（4）：61?64.

[8] 孙凤，张琪，徐方超.激光光路控制电磁作动器的模糊 PID控制特性分析[J].兵工学报，2019，40（2）：430?435.

[9] 魏小宇，郑晟.运用灰色预测与模糊加权PID的反应釜温度控制[J].重庆理工大学（自然科学），2019，33（2）：82?85.

[10] 张占立，郑肖莉，王恒迪，等.模糊自适应PID控制器在材料低周疲劳试验机中的应用[J].轴承，2019，33（2）：51?55.