基于四元数的四旋翼飞行器姿态解算研究

盛广润 高国伟 张伯源

摘  要： 四旋翼飞行器的飞行控制效果取决于姿态信息获取的准确性，所以姿态解算是飞行器研究的关键技术。针对目前飞行器高动态特性和复杂环境下的姿态解算误差较大的问题，提出一种基于四元数的二阶互补滤波算法，通过增加一个PI反馈控制环节，能更好地利用多传感器进行姿态融合，使经典互补滤波算法中的低通阻带衰减速度过慢、陀螺仪漂移等问题得以改善。同时文中自主设计了IMU系统，完成数据采集和姿态解算算法的实现，分别进行三轴转台实验，改进后姿态解算的结果表明，无论是在静态还是动态环境下，俯仰、横滚角的误差小于0.5°，验证了该算法的可行性。

关键词： 姿态解算; 四旋翼飞行器; 四元数; 互补滤波; 姿态融合; IMU系统设计

中图分类号： TN967.6?34; V219                  文献标识码： A                      文章编号： 1004?373X（2020）14?0008?05

Research on quadrotor attitude calculation based on quaternion

SHENG Guangrun1， GAO Guowei1，2， ZHANG Boyuan1

（1. Key Laboratory of Sensors， Beijing Information Science and Technology University， Beijing 100192， China;

2. MOE Key Laboratory of Modern Measurement and Control Technology， Beijing Information Science and Technology University， Beijing 100101， China）

Abstract： As the flight control effect of the quadrotor depends on the accuracy of the attitude information acquisition， the attitude calculation is the key technology of aircraft research. In allusion to the large attitude calculation error in the complex environment and high dynamic feature of aircraft， a second?order complementary filtering algorithm based on quaternion is proposed. The multi?sensor attitude fusion can be better utilized by adding a PI feedback control link， and the low?pass stopband attenuation speed and gyroscope drift in the classical complementary filtering algorithm are improved. The IMU system is designed independently， and the data collection and attitude calculation algorithm is completed. The three?axle table experiment is conducted respectively， and the results of the improved attitude calculation show that pitch and roll angle errors are less than 0.5° in both static and dynamic environments. It proves the feasibility of the algorithm.

Keywords： attitude calculation; quadrotor; quaternion; complementary filter; attitude fusion; IMU system design

0  引  言

四旋翼飞行器集合了不同飞行器的优点，凭借其结构简单、使用方便、成本低、便于操作等特点，已经被广泛应用在各行各业。如今针对四旋翼飞行器的研究不止限于熟知的军事、工业领域，更多的被应用到航拍和物流行业中，产生了巨大的商业价值，因此众多的科研院校和商业国内公司都争相投入到四旋翼的研发生产当中。

而在研究当中关键项目之一是四旋翼飞行器的姿态解算研究[1]。因为四旋翼飞行器在飞行的过程中，不仅会受到自身欠驱动系统的影响，也易受到噪声、空气阻力等复杂环境的干扰，导致姿态信息的获取增加了难度，而姿态信息获取的精准性是相应飞行器的独立飞行最基本的前提，所以姿态解算研究的重要性不言而喻。

在姿态解算中，卡尔曼滤波器的应用较为广泛，文献[2]通过卡尔曼滤波（Kalman Filtering） 融合陀螺仪和加速度计数据，递推计算出最优估计值来修正输出误差。但是飞行器系统要满足非线性系统和高斯白噪声的前提。因此扩展卡尔曼（EKF）提出，应用在非线性系统中[3]。但是EKF算法计算量大，在线性化假设无法成立的情况下，不满足四旋翼飞行器高机动、实时性的要求。而互补滤波算法简单有效，易实现传感器测量精度。四元数的旋转特性解决了飞行器姿态解算中的奇异性问题。

本文自主设计了以嵌入式MEMS控制器和惯性测量单元（Inertial Measurement Unit，IMU）组合的系统平台，采用四元数方法描述系统模型，提出了一种基于四元数的改进型互补滤波算法，致力于降低计算的复杂性和难度，提高滤波的效果。通过三轴转台实验和实物飞行测试，验证本文提出的算法可以适用于四旋翼飞行器系统，能提高姿态解算的效率和精度。

1  四元数法的姿态解算

姿态被用来描述载体坐标系和参考（地理）坐标系之间的角位置关系，四旋翼飞行器姿态解算则是飞行器的载体坐标系相对地理坐标系的姿态矩阵问题求解。

1.1  坐标系定义

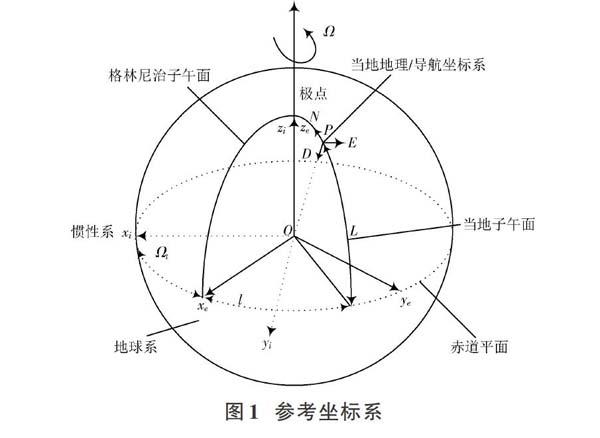
根据参考坐标系，才能确定物体的速度、姿态、位置等信息。在惯性导航中，常用的有5种坐标系，分别为地球、惯性、载体、地理、导航坐标系[4]。参考坐标系如图1所示。

地球坐标系（[O?xeyeze]）：将地球中心作为坐标系的原点，坐标轴始终与地球维持一致。其中，[xe]和[ye]沿地球的赤道平面和格林尼治子午面的交线[5]，[ze]的方向平行于地球的极轴方向，并以地球自转角速度相对于地心惯性坐标系旋转。

导航坐标系（[O?xnynzn]）：即当地的地理坐标系，坐标的原点位于P点，坐标轴指向北、东和当地垂线方向（向下）。通常把导航坐标系相对于地球固连坐标系的旋转角速率称为转移速率，速率的大小取决于P点相对于地球运动的快慢。

载体坐标系（[O?xbybzb]）：不同于导航坐标系的“东北天”，机体坐标系取载体的“前左上”，描述其姿态的角度分别为横滚（Roll）角γ、俯仰（Pitch）轴θ和航向（Heading）角ψ。

1.2  四元数姿态表示方法

四元数由实数和复数组合构成：即一个实数单位和三个虚数单位组成的四维向量，可以用来表示刚体和坐标系在三维立体空间里的姿态方向。表达式如下：[qnb=q0q1q2q3     =cosθ2-γxsinθ2-γysinθ2-γzsinθ2] （1）

式中：[q0]是标量部分的四元数系数，其大小等于坐标系旋转角度一半的余弦值，是四元数的标量部分的系数;[q1]～[q3]表示矢量的部分;[θ] 是矢量在动坐标系上轉动的角度值[6]。

通过归一化的四元数可以计算出坐标轴旋转矩阵：

[Cbn=2q20-1+2q212（q1q2-q0q3）2（q1q3-q0q2）2（q1q2+q0q3）2q20-1+2q222（q2q3-q0q1）2（q1q2-q0q2）2（q2q3+q0q1）2q20-1+2q23]             （2）

得旋转矩阵为：

[Cnb=（Cbn）-1=（Cbn）T] （3）

欧拉角由四元数方法表达为：

[ψ=arctan2（q1q2+q0q3）2q20-1+2q22θ=arcsin2（q2q3+q0q1）γ=arctan-2（q1q3+q0q2）2q20-1+2q23] （4）

式中，四元数方法描述转动、估计姿态都优于其他方法，因为始终可以避免奇异性，且仅需要4个参数进行计算，计算效率得以提升。载体系相对于地理系的角度求解，可以被看作是由地理系只经过一次旋转形成载体系，四元数方法可以支持这种等效计算。

2  姿态算法实现

2.1  互补滤波

姿态解算需要采用加速度计、陀螺仪采集的数据进行计算，陀螺仪的测量值是载体坐标系的角加速度，加速度计的测量值则是其线加速度。各自都有缺点，特别是在飞行器载体因干扰产生抖动的时候，来自陀螺仪、加速度计会更容易产生高斯白噪声;单个陀螺仪漂移误差与工作时间产生正比的递增，表现形式为误差随时间增长而累积，但是在较短的时间内可获取较为精确的数据;加速度计与其相反，静态特性好，但是短时间内的精度表现较差，无法满足飞行器易抖动的特性。

总结为两者在频率上呈互补关系，互补滤波则是将加速度计和陀螺仪分别在不同频率上的优势融合。即利用加速度计测得短时间的瞬时值来补偿陀螺仪长时间积累出现的漂移误差[7]。其原理图如图2所示。

设[θ]为姿态角，融合后的姿态角估计值为：

[θ=sωgs+kP·1s+kPs+kPθα]  （5）

式中：[ωg] 是陀螺仪测量的角速度值;[θα]则是角度值，来自加速度计测量;高通滤波器为[ss+kP];低通滤波器为[kPs+kP]。高通滤波器的作用是减小低频下陀螺仪的漂移误差，低通滤波器则是限制高频下的加速度计噪声[8]。式（5）可经过反拉普拉斯变换得：

[θ=kP（θα-θ）+ωg] （6）

观察式（6），互补滤波是通过调整[kP]值改变滤波器的截止频率，达到对陀螺仪、加速度计所占比重的处理。

2.2  互补滤波改进设计

经过分析，第2.1节介绍的一阶互补滤波可以在某个阶段抑制陀螺仪积分产生漂移误差、降低高频噪声。但是文献[9?11]等人对经典互补滤波进行了研究，得到以下结论：由于其低通阻带衰减缓慢，四旋翼飞行器具有高动态性，固定的调节参数设置无法在所有的情况下得到最优的估计值。所以一阶互补滤波器不能随时有效消除系统误差。

因此在互补滤波原理的基础上，针对传统互补滤波应用在姿态解算上的不足，结合误差来源，提出在互补滤波基础上增加一个PI（比例积分）反馈控制环节，完成互补滤波的改进。理论上可以加快低通阻带的衰减速度，可以在不同的情况下，动态地调整补偿的系数：如果处于匀速状态，增大加速度计的所占权重;高动态时，减小加速度及占的比重，增大陀螺仪比重。

整个流程即是先将加速度计解算出的角度与最终角度产生的误差实现PI控制，促进误差的修正。修正后和陀螺仪解算出的姿态角相加后再进行积分得到一个新姿态角。改进后的互补滤波算法如图3所示。

算法的实现过程如下：

1） 首先对加速度计测量的三维向量进行规范化：

[A=AA=αxαyαz]  （7）

对载体坐标进行转换到地理坐标系后，可得到载体坐标系下重力加速度的三维向量：

[A=AA=αxαyαz]     （8）

2） 加速度计的测量值向量[A]和陀螺仪积分后的姿态估计向量[A]之间的误差向量利用向量间的叉积表示：

[Eα=A×A=eαxeαyeαz]

改进增加的比例积分环节可以求解得出陀螺仪的漂移补偿向量：

[Δ=δxδyδz=kPeαx+kI∫eαxkPeαy+kI∫eαykPeαz+kI∫eαz]

如上所述可修正误差。

3） 通过一阶龙格库塔法求解四元数微分方程，求解出的四元数的更新方程为：

[q0q1q2q3t+Δt=q0q1q2q3t+12Δt-ωxq1-ωyq2-ωzq3ωxq0-ωyq3+ωzq2ωxq3+ωyq0-ωzq1-ωxq2+ωyq1+ωzq0]          （9）

4） 將漂移误差向量代入到式（9）中，得到角速度微分四元数。

5） 对更新后的四元数积分规范化处理，由式（4）求解得出姿态角估计值。

3  实验验证与分析

3.1  试验平台

试验平台以自主开发的四旋翼飞行控制系统为主体，主要包含三轴加速度计、三轴陀螺仪、三轴磁力计、ARM处理器、通信模块、电源模块等部分。系统整体硬件框架如图4所示。

试验系统平台利用处理器对姿态信息进行融合，通过串口输出到上位机显示姿态角。主控选用STM32F103处理器，性价比高，运算速度快;陀螺仪选用ADXRS450，高分辨率（0.015 （°）·s-1·g-1），通信接口选用SPI;加速度计选用ADXL355，高分辨率（256 000/g），SPI通信;磁力计传感器采用MAG3110，分辨率高：

0.1 μT/LSB，通信接口为I2C。设置串口波特率为115 200 b/s、8位数据位、1位停止位、无奇偶校验。利用上位机软件接收姿态数据，自主研发IMU系统实物图如图5所示。

3.2  测试试验设计

本试验将飞行器的IMU惯性测量单元固定在SGT320E三轴多功能转台进行测试，主要针对飞行器的俯仰角和滚转角试验。SGT320E三轴转台在飞行器研制领域中起到关键性的作用[12?13]，能够提供精准的航姿变换轨迹、实时的姿态信息;复现飞行器运动的各种动力学特性。实验室三轴转台装置如图6所示。

实验过程：首先将四旋翼飞行器的IMU测量单元固定在转台上，保证其姿态不会发生改变，进行静态测试;结束静态测试阶段进行动态测试，分别测试IMU测量系统的横滚角、俯仰角。姿态传感器在一定时间完成数据采集后，通过SPI通信方式与主控芯片进行传输[14]。对姿态数据进行解算后，通过RS 232串口上传到上位机上进行姿态角数据的显示[15]。

静止状态下：将三轴转台归零，处于闲置状态，运行程序，采取约45 s的数据，可以看出来图7、图8中，无论是俯仰角还是横滚角，改进后的算法输出的数据都在0°附近几乎没有发散，误差相对较小，经足够数据验算取平均值。经典互补滤波下：横滚角误差、俯仰角误差分别为0.352 1°和0.384 3°;改进型互补滤波横滚角、俯仰角误差为0.129 5°和0.087 5°。得出结论，在静止状态下，改进后互补滤波算法精度优越，改善了陀螺仪的漂移误差问题。

动态测试条件下，为了观察两种算法在姿态发生变化时的响应性能，通过对不同角度进行动态测试，上位机输出不同算法解算的姿态角度数据，为了动态数据采集的完整性，程序运行后等待1～3 s开始转动转台。首先设置转台进行横滚角转动，图9和图10分别是0°～40°，40°～0°（回零）数据波形。波形表示在转动的瞬间，改进后互补滤波并没有出现较大的超调量，在6～8 s时候波动的幅度要远小于原始的互补滤波算法;在设置40～0°的动态测试中，为了观察不同速度下姿态角的变化，加快了转台的转速，结果发现改进型算法仍然具有较好的稳定性能，满足飞行器的高动态性能下的解算要求。

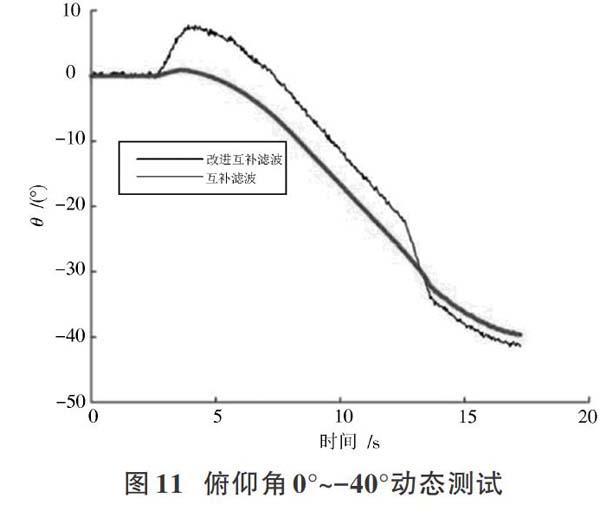
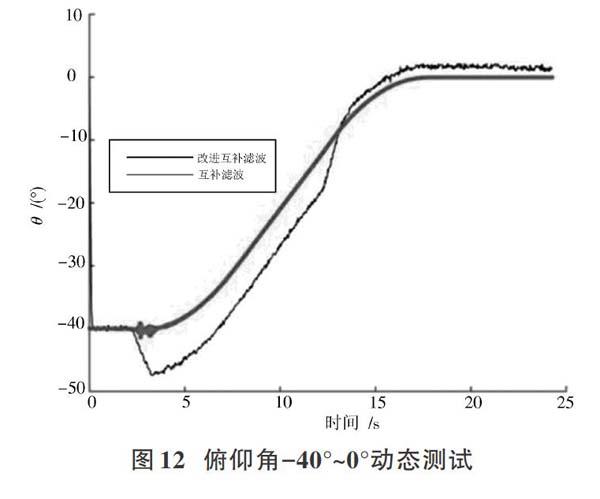
考虑到有负角度的情况，对俯仰角进行0°～-40°，

-40°～0°的对比姿态变化，如图11和图12所示。同上，可以看出改进后互补滤波算法的优越性，动态测试中，数据波动相对平滑，角度变化的过程中没有出现很大的数据波动和较大的动态误差。

4  结  语

本文基于四元数的姿态表达方法，通过与姿态旋转矩阵的关系获得姿态角。针对四旋翼姿态解算误差较大的问题，通过分析，提出一种改进型互补滤波对飞行器的姿态信息进行误差修正，加快低通阻带衰减速度。本文自主设计了基于多传感器的IMU测量系统，对采集到的姿态数据进行融合，分别在静态和动态的条件下进行三轴转台试验，经过数据记录和分析，结论是基于四元数的改进型互补滤波算法能够抑制干扰误差，有效地提升了无人机姿态融合的准确度，可以有效降低四旋翼的姿态解算上的误差，满足四旋翼飞行器实际飞行的姿态估计精度要求。

参考文献

[1] 张谦，邬依林.基于智能视觉的无人机导航技术研究[J].现代电子技术，2018，41（16）：132?134.

[2] 谭祖锋.惯性导航技术的新进展及其发展趋势[J].电子技术与软件工程，2019（5）：76.

[3] 薄江辉，王茂锋.GPS与惯性导航系统的组合应用研究[J].通讯世界，2019，26（6）：254?255.

[4] 史凯，刘马宝.捷联惯导四元数的四阶龙格库塔姿态算法[J].探测与控制学报，2019，41（3）：61?65.

[5] ZHANG Lihong， MASEK Vlastimil， SANATDOOST Nikoo?Naeemi. Structural optimization of z?axis tuning?fork MEMS gyroscopes for enhancing reliability and resolution [J]. Microsystem technologies， 2015， 21（6）： 1187?1201.

[6] 卢毅.小型航姿参考系统设计[J].传感器与微系统，2019，38（4）：117?120.

[7] 秦永元.惯性导航[M].北京：科学出版社，2006.

[8] WANG D J， WANG G C， JIE W U. Fixed?interval smoothing post?processing algorithm for low?cost MEMS?based integrated navigation system [J]. Journal of Chinese inertial technology， 2017， 25（1）： 97?102.

[9] 周彬.MEMS?INS/GNSS组合导航系统研究[D].南京：南京航空航天大学，2017.

[10] LUIGI Palatella， FABIO Grasso. The EKF?AUS?NL algorithm implemented without the linear tangent model and in presence of parametric model error [J]. Software X， 2018， 7： 28?33.

[11] FENG Kaiqiang， LI Jie， ZHANG Xiaoming， et al. A new quaternion?based Kalman filter for real?time attitude estimation using the two?step geometrically?intuitive correction algorithm [J]. Sensors， 2017， 17（9）： 2146.

[12] 康跃然，肖本龙，傅亦源，等.三轴转台系统姿态变化下指向误差建模与分析[J].制造业自动化，2018，40（12）：135?139.

[13] 陈传俊，陈志高.基于振动台的加速度传感器灵敏度的标定[J].大地测量与地球动力学，2013，33（z1）：168?171.

[14] 孙佳，邹靖，胡桐.基于24位置的MEMS惯性传感器快速标定方法[J].压电与声光，2019，41（3）：440?444.

[15] 王日俊，曾志强，党长营，等.一种基于STM32的机载惯性稳定云台的设计[J].现代电子技术，2018，41（12）：145?148.

[16] 朱新宇，陶庭叶，姜冬致.基于GPS/MEMS惯性传感器的消防员室内定位研究[J].合肥工业大学学报（自然科学版），2018（7）：949?955.