高层建筑在爆破地震波作用下振动传播规律
2020-07-23吴桂义高正华袁玉宝
雷 振,贺 路,吴桂义,高正华,袁玉宝
(1.贵州理工学院矿业工程学院,贵阳 550003;2.贵州大学矿业学院,贵阳 550025)
在工程上人们一直关注着许多问题,而爆破地震波对高层建筑物的影响一直是重大研究对象之一,长时间以来,为了解决这一问题,国内外许多专家学者从问题的一般规律出发来研究,展开了大量的研究工作。爆破地震波振速和频率是首要的研究对象,加强对各种爆破条件下爆破地震波的特性分析和建筑物破坏现象、破坏特征的宏观调查以及爆破地震波的特征参数研究,以调查资料和现场爆破振动测试数据为依据;通过数据的分析处理,研究爆破地震波影响作用下建筑物的振动传播规律[1-4];用量纲分析得出爆破振动峰值速度或加速度关于爆心距与药量的经验公式,并在此基础上进行爆破振动的预测与评估;著名的萨道夫斯基公式和爆破地震波强度衰减规律方程[5]都是针对振动进行的研究工作。随着对爆破地震效应的控制愈来愈严格,在今后的一段时间内,爆破地震波对建筑物的影响研究仍将是工程爆破领域的热点问题之一[6-9]。目前,对这一问题的研究方法和角度也呈现出多样化的态势。人们认为高程在建筑物的振动传播规律中是一个不可忽视的重要因素,高程影响系数和与爆破有关的系数对爆破振动的影响是不容忽视的,应加强对振动演化规律的研究。考虑到高边坡条件,前人提出了高程修正公式[10],即
(1)
式中:v为质点振动速度,cm/s;Q为最大段药量,kg;H为爆源至测点的垂直距离,m;R为爆源至测点的水平距离,m;K,α为与地形和地质条件有关的参数;β为高程影响系数。
上述公式在爆破工程中得到了广泛的应用。
鉴于此,在贵阳市观山湖区百花大道延伸道路边坡的爆破工程进行现场试验,通过高程修正公式,分析在距爆心不同距离、距地面高差不同情况下,在建筑结构中爆破地震波作用所引起的振动传播规律,为控制爆破振动以及预测结构是否破坏提供参考依据。
1 爆破现场试验
1.1 试验场地概况
试验场地位于贵州省贵阳市观山湖区百花大道边坡的山体和一小区的五幢高层建筑。爆破开挖采用2号岩石乳化炸药,由于该边坡对面是高层建筑小区,采用了控制爆破减少振动,并对其进行了实时监控。高边坡主要为中硬岩石,采用深孔控制爆破和逐孔起爆的方法进行开挖,爆破参数如表1所示。

表1 爆破参数
1.2 监测点布置
共有5个传感器,需要分批测量,在高边坡坡底对面小区的一至五幢分别布置1#~5#水平监测点,垂直方向每幢建筑的1、5、9、13、17层分别布置1#~5#监测点(见图1);测点参数如表2所示。

图1 测点布置Fig.1 Layout of measuring points

表2 测点参数
爆破振动监测方案1,测点分别布置在离爆源最近的楼房130、183、236、289、342 m处,沿爆源中心的径向同一条直线,因振动幅值不大,频率不是很高,只需将传感器直接置于地表,周围用石膏粘附即可,从而保证了传感器与建筑物一起振动。每次在起爆前打开仪器,以防止仪器的误触发。每幢楼房布置一个测点,每个测点之间相隔距离53 m,测点在同一楼层,安放在楼道处,因爆破振源位置和距离不同,每次测得振动速度及频率也不同。
爆破振动监测方案2,共有5个测点布置在每幢楼距地面高差2、14、26、38、50 m处,每次测试时,测点在同一幢楼房,沿爆源中心的垂向一条测线,因振动幅值不大,频率不是很高,只需将传感器直接放置楼道处,周围用石膏粘附即可,每次测试严格要求测点的垂直方向保持在一条直线上,因爆破振源位置和距离不同,每次测得振动速度不同。
2 试验数据与分析
2.1 试验结果
试验选取测点3个方向振动速度进行研究,数据如表3所示。

表3 测点振动速度数据
2.2 爆破振动速度衰减规律分析
2.2.1 爆破振动速度随水平距离的规律
爆破振动速度随着水平距离的变化趋势如图2~图3所示。
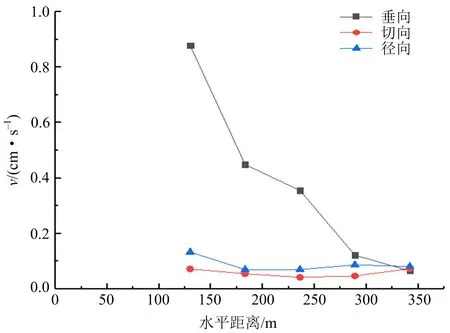
图2 高差为50 m的振速Fig.2 Vibration velocity with height difference of 50 m

图3 高差为2 m的振速 Fig.3 Vibration velocity with height difference of 2 m
由图2可知,测点在高于地面(高差50 m)随着水平距离的增加,垂向振速逐渐减小;除了300~350 m处最后一测点三向振速,垂直方向振速恒大于水平切向和径向振速;垂向速度衰减趋势比较显著。
由图3可知,测点在接近地面(高差2 m)爆破振动速度随水平距离的增加,垂向和径向逐渐减减小,切向振速先减小后增加,从数值上来看,变化不大;垂向振速恒大于切向和径向振速。垂向速度衰减趋势比较显著。
2.2.2 爆破振动速度随高差变化的规律
爆破振动速度随着高差变化的趋势如图4~图5所示。

图4 水平距离130 m振速随高差变化Fig.4 Vibration velocity changes with height difference at a horizontal distance of 130 m

图5 水平距离342 m振速随高差变化Fig.5 Vibration velocity changes with height difference at a horizontal distance of 342 m
由图4可知,测点接近爆源(水平距离130 m)垂向振动速度随着高差的增大而逐渐增大。垂向振速恒大于切向振速和径向振速;然而切向振速和纵向振速随着高差的增加基本保持平稳不变,改变测点的高度基本不会改变测点的切向和径向的振动速度。
由图5可知,测点远离爆源(水平距离342 m)垂向振动速度随着高差的增大而逐渐增大。分析表明:垂向振速随高差的增加而逐渐增大,切向和垂向振速变化规律不能准确判断。
3 高差修正公式分析
试验选取测点3个方向中的最大振动速度进行分析,数据如表4所示。

表4 测点最大振动速度
由表4可知,在爆心距130~342 m范围,当测点放置距爆心水平距离130 m时,高差从高到底,测点振速基本都是逐渐减小的,但测点在爆心水平距离为342 m时,衰减规律已经没那么明显,甚至是从高到低还出现很多增大的情况,这表明爆破的衰减规律是在一定范围内的,超出这个范围,衰减趋势性减弱。
用式(1)拟合表4 的数据得到测点在不同距地高差下,最大振动速度随着水平距离变化的非线性拟合曲线(见图6~图10)。

图6 高差2 m的变化规律Fig.6 Variation of height difference of 2 m

图7 高差14 m的变化规律Fig.7 Variation of height difference of 14 m

图8 高差26 m的变化规律Fig.8 Variation of height difference of 26 m

图9 高差38 m的变化规律Fig.9 Variation of height difference of 38 m

图10 高差50 m的变化规律Fig.10 Variation of height difference of 50 m
分析表明:不管测点在哪个高差位置,振速都随着水平距离的增加而减小。拟合得出的汇总数据如表5所示。

表5 拟合汇总Table 5 Fitting summary
由表5分析得到,衰减系数和高程影响系数随高差的变化如图11~图12所示。

图11 衰减系数随高差变化Fig.11 Attenuation coefficient changes with height difference

图12 高程差影响系数随高差变化Fig.12 Elevation influence coefficient changes with height difference
由图11可知,随着高差的逐渐增加,衰减系数α整体上逐渐增大,测点随着高差的增加,同一高差的测点随着水平距离的增加,衰减效果更加显著。分析表明:得出衰减系数α随着距地高差的减小而逐渐减小。
由图12可知,测点远离地面,等于是爆源和测点相对高差较大时,高程影响系数β较大,中间位置出现了一个低谷,呈一个先降低后增加的趋势。分析表明:高程影响系数β在爆源至测点的垂直距离最大时也最大,随垂直距离的增加,先降低后增加,出现了一个低谷。
4 结论
1)垂向振动速度随着水平距离的增加逐渐减小,整体上垂向振动速度大于径向和切向振速。
2)在水平地面时,随着爆心水平距离的增加,振动速度逐渐降低。切向和径向振速衰减趋势较小。
3)在测点同一楼层时,水平距离不变,随着距地高差的增加,振动速度也越来越大。
4)衰减系数α整体上随着高差的增大而增大。
5)高程影响系数β呈现先减小后增加的趋势。
