时间分数阶扩散方程的变密度网格弱Galerkin有限元数值模拟

2020-07-23王怡昕朱爱玲

山东师范大学学报（自然科学版） 2020年2期

关键词：剖分范数数值

王怡昕朱爱玲

( 山东师范大学数学与统计学院，250358，济南 )

1 引言

考虑以下初边值问题:

(1)

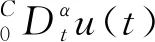
(2)

Γ(·)表示Gamma函数. 为了书写简便，以下将省略x和t.

分数阶微分方程是含有非整数阶导数项的微分方程，在物理，生物，化学和机械工程等领域发挥着越来越重要的作用. 扩散方程是模拟粒子随机游走规律的，分数阶扩散方程则是描述这种现象的一种更有效的模型. 求解分数阶微分方程的精确解是极其困难的，因此，数值解法被许多学者关注和研究. 目前求解分数阶微分方程数值解的主要方法包括有限差分法[1-4]、谱方法[5,6]和有限元法[7-10]等等. 国内外许多学者在相关领域取得了优异而有效的研究成果， Luchko[11]等人考虑无界域中广义时间分数扩散方程的初边值问题. 刘法旺[12]等人求解多项式分数阶扩散方程的二阶中心差商并分析了差分格式的收敛性.刘思宇和陈焕贞[13]对时空分数阶扩散方程使用最小二乘混合型有限元法建立了相应的有限元格式，并证明了离散解的存在唯一性和收敛性.

王军平和叶秀[14]针对二阶椭圆方程，提出了弱Galerkin有限元方法，在该方法中，其数值解的弱连续性是通过引入广义弱微分来实现. 之后弱Galerkin有限元方法被应用到一维多项时间分数阶扩散方程[15]，抛物型积分微分方程[16]，二阶椭圆界面问题[17]，双调和方程[18]等等. 本文考虑在三角网格剖分下，使用弱Galerkin有限元方法数值模拟有奇异性的二维单项时间分数阶扩散问题.

文章的结构如下;第2节给出弱Galerkin有限元格式和时间分数阶扩散方程的全离散弱Galerkin有限元格式；第3节，证明弱Galerkin有限元格式的稳定性；第4节给出弱Galerkin有限元全离散的H1范数和标准的L2范数的误差估计，第5节给出数值算例验证理论结果.

我们使用标准的Sobolov空间Hm(m≥0)，及与此空间相关的内积，给出以下记号:

半范为

范数为

对于可测函数v:[0,T]→Hm(Ω)，令

2 弱Galerkin有限元格式

令Th为任意多边形构成的区域Ω的有限元剖分，假定所有单元T∈Th为连通多边形，且满足正则性条件.Th包含了内部区域T0和边界∂T，对任意单元T∈Th，Pj(T0)和Pj(∂T)分别表示在T0和∂T上次数不超过j的多项式集合.Sh(j)为弱函数空间，定义如下

Sh(j):={v={v0,vb}:v0∈Pj(T0),vb∈Pj(∂T), ∀T∈Th}.

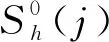
设∑h={q∈(L2(Ω)2:q|T∈W(T,j+1),∀T∈Th}，空间W(T,j+1)表示在T上次数不超过j+1的向量值多项式集合的子空间. 对任意v={v0,vb}∈Sh(j)，v在每个单元T上的离散弱梯度dv∈∑h由下式给出[13]：

(3)

对任意T∈Th，Qhu={Q0u,Qbu}是H1(T)到Pj(T0)×Pj(∂T)的局部L2投影. 单项时间分数阶扩散方程改写为以下变分形式

(4)

对时间区间(0,T]进行剖分，当n=0,1,…,N时，tn=T(n/N)r，其中r为网格分级常数，a(·,·)为双线性形式，

(5)

(6)

其中系数{pn,k}记为

(7)

使用中值定理，有pn,k≥pn,k+1，和

(1-α)(tn-tn-k+1)-α≥pn,k≥(1-α)(tn-tn-k)-α.

(8)

Rτg(tn)的误差估计在文献[19]中已经给出.

‖Rτg(tn)‖≤CN-min{2-α,rα}.

(9)

(10)

(11)

(12)

Eh是椭圆投影算子，将在第4节介绍.

3 弱Galerkin有限元的稳定性

引理2弱Galerkin有限元格式(10)的解满足

(13)

和

(14)

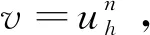
对上述等式变形，得到

根据Cauchy-Schwars不等式，得

等价于

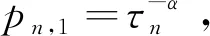
根据Cauchy-Schwars不等式，得

整理得

(15)

根据定义，对不等式(15)重新改写得

根据Cauchy-Schwars不等式，得

化简整理，即得

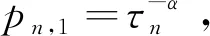
定义一个实数ζn,j，其中n=1,2,…,N和j=1,2,…,n，记

(16)

由(8)式可得，对任意n,j，都有θn,j>0.

定理1当1≤n≤N时，由(10)式，(11)式和(12)式定义的弱Galerkin有限元格式的解是稳定的，即

(17)

和

(18)

证固定1≤n≤N. 首先证明弱Galerkin有限元格式L2的稳定性. 当n=1时，有

直接由不等式(13)得到.

固定n=2,3,…,N. 假设在(17)式中当i=2,3,…,n-1成立，由归纳法，得

通过归纳论证，不等式(17)成立.

类似可得(18)式成立.

由文献[19]，可知(16)式定义的ζn,j满足以下引理3.

引理3若β≤rα，则当n=1,2,…,N时，有

4 标准的L2范数和离散的H1范数的最优误差估计

在单项分数阶扩散问题的数值方法研究中，为了得到最优误差估计，引入椭圆投影Ehu={E0u,Ebu}，满足以下形式

(19)

由文献[13]中误差估计的结果，可得以下引理4.

引理4假设u∈L(0,T:Hs+1(Ω))是分数阶扩散方程(1)的精确解，Ehu是椭圆投影算子，则存在一个独立于h的常数C，使得

‖Qhu-Ehu‖≤Chm+1‖u‖m+1,,

(20)

和

‖d(Qhu-Ehu)‖≤Chm‖u‖m+1,.

(21)

(19)式两端关于t求导，利用文献[13]中误差估计的方法，可得以下引理5.

引理5设ut∈L(0,T:Hs+1(Ω))，则存在一个独立于h的常数C，使得

‖(Qhu-Ehu)t‖≤Chm+1‖ut‖m+1,,

和

‖d(Qhu-Ehu)t‖≤Chm‖ut‖m+1,.

接下来给出在弱Galerkin空间中标准的L2范数和离散的H1范数的最优误差估计.

(22)

和

(23)

证固定1≤n≤N，将误差写为两项之和

记ξn=un-Ehun. 当t=tn时，等式(10)减去等式(4)，并使用等式(19)，得到误差方程

(24)

对误差方程重新改写，得

(25)

(26)

根据Pτ(∂t)的定义，得

(27)

由引理5，得

(28)

利用定理1的稳定性和引理3，再由ξ0=0，dξ0=0，以及当n=0,1,…,N时，ξn|∂Ω=0，有

(29)

同理得

(30)

由引理4和三角不等式得

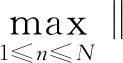
5 数值实验

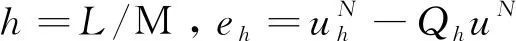
精确解u(x,y,t)=(tα+t3)sinxsiny满足Dirichlet边界条件，其初始条件是u0(x,y)=0.

‖eh‖和‖deh‖分别是给出的L2范数和离散的H1范数. 它们的收敛阶分别由和给出. 算例的结果见下列表格，在表1中，固定时间网格剖分N, 取网格分级常数r=(2-α)/2α，当空间步长逐渐减小时，弱Galerkin格式的数值解在L2范数和离散的H1范数中的最优速率O(h2)和O(h)与理论结果一致. 表2为固定时间步长N，取网格分级常数r=(2-α)/2α，当α=0.8及α=0.9的离散的H1范数的弱Galerkin有限元方法的误差.