改进灰狼优化算法在变桨距自抗扰控制中的应用

宋文静， 谢 源， 黄文君， 李容爽

（上海电机学院 电气学院， 上海 201306）

0 引言

近年来，风电产业迅速发展，变桨控制系统作为风电机组的重要组成部分受到广泛关注。 风电场内风速随机变化导致风电机组的输出功率也随之波动，不能较好地稳定于额定功率值处，当风机并入电网后， 对电网的安全稳定性产生一定的影响。 传统PID 控制虽已广泛应用于变桨领域，但在大惯性、 强耦合的风力发电系统中的控制效果并不理想[1]，[2]。 针对这一问题，国内外学者将一些模糊控制[3]、鲁棒控制[4]、自抗扰控制[5]应用到风电变桨控制中，并取得了一些成果。

自抗扰控制技术是一种非线性控制方法，它不需要被控对象精确的数学模型， 通过对系统内部扰动及外部扰动进行估计与补偿从而消除系统总扰动的影响，具有较好的控制效果[6]。 鉴于自抗扰控制器高效、 快速解决问题以及具有较好的抗扰动能力， 其已经被应用到风电机组变桨距控制应用中[7]，[8]。但自抗扰控制器（ADRC）参数多，单纯的靠人类经验对繁杂的参数进行整定难度很大。因此，相关学者提出将PSODE 混合算法[9]、改进蜂群算法[10]应用到ADRC 中，实现对参数的自寻优整定。

为实现ADRC 参数的自寻优整定，本文提出了一种改进灰狼优化算法的变桨距自抗扰控制器参数整定方法。 该方法利用粒子群算法对灰狼算法进行改进， 并用于风电机组变桨距自抗扰控制器的参数整定中。仿真结果证明，该方法具有较好的参数自寻优能力， 同时整个系统的抗干扰能力得到明显提升。

1 风力发电机组建模

由空气动力学可知， 风轮从风中捕获的功率（Pw）为

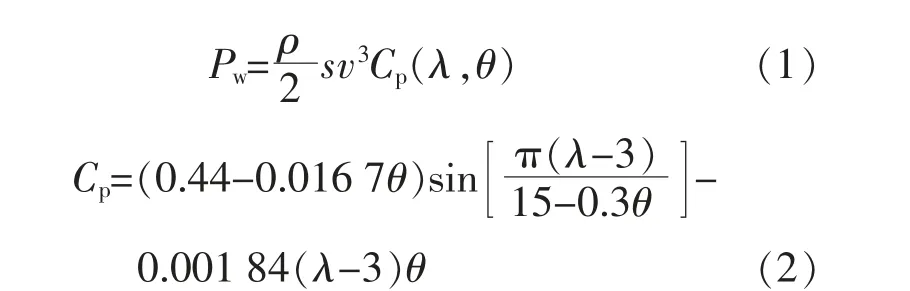
式中：ρ 为空气密度；s 为半径为R 的风轮叶片扫过的面积；λ 为叶尖速比；θ 为桨距角；v 为风速；Cp为风能利用系数。

以永磁同步风电机组作为研究对象， 风轮和发电机的轴直接相连， 简化的直驱风电机组力学模型为

式中：Tm为风轮机械转矩；Te为发电机电磁转矩；J 为风机的转动惯量；ω 为风轮转速。

将风力发电机当做理想电机处理，经过Park变换后，发电机基于d-q 旋转坐标的数学模型为

式 中：ud，uq分 别 为d，q 轴 电 压；id，iq分 别 为d，q轴电流；Ld，Lq分别为d，q 轴电感；Ra为定子电阻；λ0为永磁体磁通；ωe为转子角速度。

风力发电机组变桨距执行机构大多采用液压装置和电机实现。 其简化的一阶惯性模型为

式中：τθ为时间常数；θr为给定桨距角。

2 风电机组变桨距自抗扰控制器设计

ADRC 是在传统PID 的基础上改进得到的一种新的控制器，它由跟踪微分器（TD）、扩张状态观测器（ESO）和非线性状态误差反馈（NLSEF）3部分组成。TD 是将传统微分器进行离散化并加以改进得到的用来跟踪目标信号的新型微分器，它通过提取输入信号的微分信号解决系统存在的超调量大的问题，为系统合理地安排过渡过程。ESO通过对系统内部扰动及外部扰动进行估计与补偿从而消除系统总扰动的影响， 体现了较强的抗干扰性能。 NLSEF 将误差信号进行非线性组合，增强系统的动态性能。

图1 为风机变桨距ADRC 结构图。 图中：Pref为给定功率；V1为Pref的追踪信号；V2为V1的微分信号；P 为实际输出功率；Z1为P 的跟踪信号；Z2为Z1的微分信号；Z3为跟踪总扰动；w 为系统外部干扰；θ0为非线性控制律计算控制量；θref为自抗扰控制器输出的桨距角；θ 为经执行机构输出的叶片桨距角值。

图1 风机变桨距ADRC 结构图Fig.1 Wind turbine variable pitch ADRC structure diagram

式中：β01，β02，β03均为ESO 的增益，β01，β02，β03的取值对系统性能有较大影响；d 为带宽；a1，a2均为非线性因子；b0为补偿因子的估计值。

β03越大，系统性能越好，但参数过大，系统的稳定性会降低。β01，β02变化幅度较小时，对系统影响不大，但如果选值不当，也会使系统产生高频振荡。 因此， 应在保障系统良好的跟踪效果下，对β01，β02，β03进行合理选择。 d，a1，a23 个参数的取值为0～1。

TD 的算法为

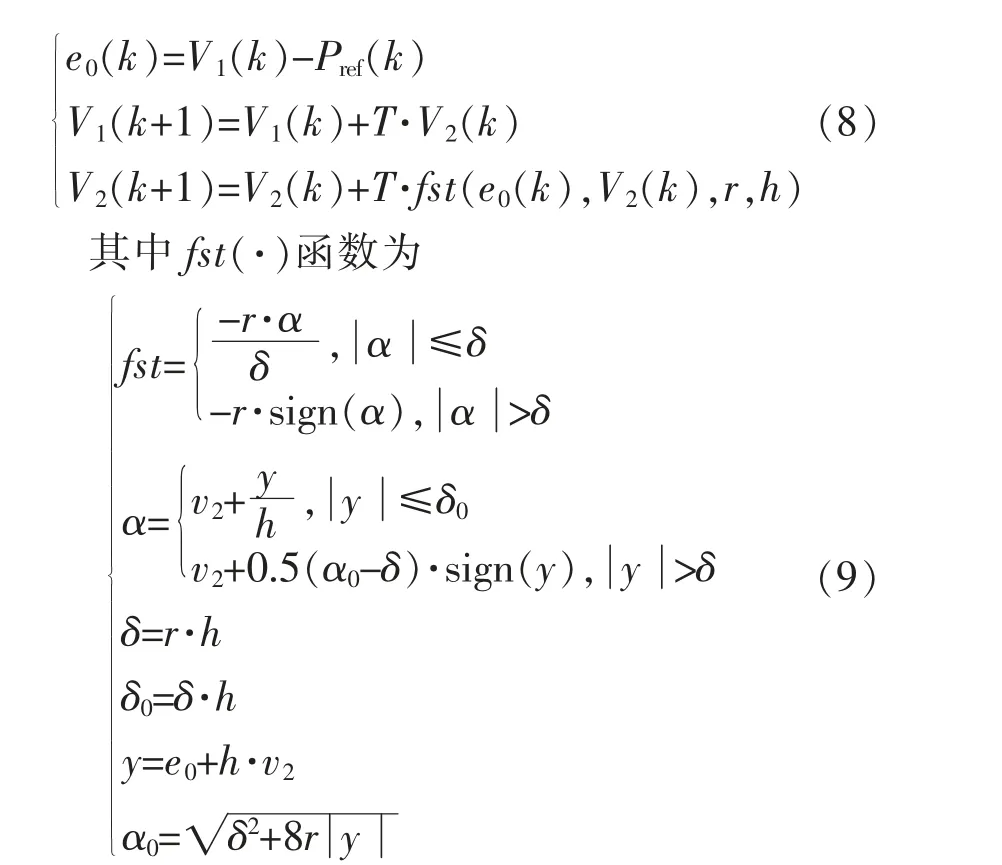
式中：T 为采样周期；r 为跟踪快慢的速度因子，可以改变系统的跟踪速度，且与跟踪速度成正比，但r 过大，会导致系统超调量增大，因此，应在跟踪速度达到系统要求情况下，选取较小的r 值；h 为决定滤波效果的滤波因子，一般情况下，h 取值与控制器采样周期T 相同。

式中：aa1，aa2均为非线性因子， 一般在0～1 进行取值；β1，β2分别为误差和误差微分的增益，β1，β2的调整与传统PID 中比例系数及微分系数的整定相似。

3 改进灰狼算法对变桨距自抗扰参数整定

3.1 灰狼优化算法

灰狼优化算法是一种根据灰狼群体捕食而提出的智能算法。与其他智能算法相似，猎物代表最优解，而每头灰狼的位置代表一个可能的解。在寻优的过程中， 根据适应度函数值的优劣程度对灰狼划分等级。 将适应度函数值最佳的灰狼个体命名为α 狼，次之的为β 狼，再次之为δ 狼，剩余的均为w 狼，α，β，δ 狼更接近于猎物的潜在位置。灰狼的等级制度在捕食的过程中起着重要作用，灰狼群体在α 狼的带领下包围猎物，β 狼、δ 狼对猎物进行攻击，w 狼全程协助攻击猎物，最终捕获猎物[11]。

灰狼捕食过程可以由以下数学模型来表示。

式中：Dα，Dβ，Dδ分别为灰狼个体与α 狼、β 狼、δ 狼的距离；C1，C2，C3均为摆动因子；A1，A2，A3均为收敛因子；Xα，Xβ，Xδ分别为α 狼、β 狼、δ 狼的位置；X 为灰狼个体的位置；X1，X2，X3分别为灰狼个体在α 狼、β 狼、δ 狼指导下更新的位置；a 为控制参数，从2 线性减 小到0；r1，r2为[0，1]间的随机向量；I 为当前迭代次数；Imax为最大迭代次数。

3.2 改进灰狼优化算法设计

在搜索空间内，α 狼、β 狼、δ 狼估计猎物的位置，其他灰狼个体在α 狼、β 狼、δ 狼的指导下更新自身的位置，能够全方位包围猎物，在灰狼群体的互助作用下，最终捕获猎物。传统灰狼算法利用α狼、β 狼、δ 狼三者指导位置的平均值完成对灰狼个体的位置更新， 却忽略了位置更新应与灰狼的指导层次和灰狼个体的搜索速度以及自身经验有关的问题，位置更新策略并不完善，使得灰狼狩猎时易陷入停滞。

粒子群算法利用粒子的自我总结和向群体中最优个体学习的特性，完成对粒子的位置更新，有较好的寻优能力。因此，本文提出将粒子群算法的位置更新策略应用到灰狼算法位置更新中， 可以有效地控制灰狼的搜索速度及搜索精度， 避免种群提前寻优停滞。

灰狼移动速度、位置更新如下式所示：

式中：n 为粒子数；D 为搜索空间维度；pi，j为灰狼个体迄今为止经历过的最优位置；w1，w2，w3均为惯性权重系数；c1r1[pi，j-xi，j（t）]为灰狼的“认知”行为；c2r2[ω1X1+ω2X2+ω3X3-xi，j（t）] 为灰狼分别向α狼、β 狼、δ 狼学习的“社会”行为。

通常对适应度函数的选取没有特别的限定，可根据要实现的目标自行设定适应度函数。 风电机组变桨距的目的是实现功率的稳定，因此，可选取系统功率期望值与系统实际功率输出值的累计误差作为适应度函数。

式中：t 为系统仿真时间；P 为系统输出功率；Pref为给定功率。

改进灰狼优化算法流程图如2 所示。

图2 改进灰狼优化算法流程图Fig.2 Improved gray wolf optimization algorithm flow chart

自抗扰控制器中的β01，β02，β03，β1，β25 个参数需要协调整定，其他的参数可以根据经验设置为固定值，因此，本文利用粒子群改进灰狼优化算法对ADRC 的5 个控制参数进行优化整定。

图3 为改进灰狼优化算法控制结构图。

图3 改进灰狼优化算法控制结构图Fig.3 Improved gray wolf optimization algorithm control structure diagram

4 仿真分析

为验证改进灰狼优化算法在变桨距自抗扰中的效果， 本文在Simulink 中搭建了一个功率为2 MW 的永磁直驱风电机组变桨距自抗扰控制器数学模型。

2 MW 永磁直驱风电机组的参数见表1。

表1 2 MW 永磁直驱风电机组的参数Table 1 System parameters of PMSG

在改进灰狼优化算法中， 设定种群规模为20，种群维数为5，迭代次数为12，灰狼算法参数与之相同。 仿真系统在采样周期T=0.001，仿真时间t=30 s 时的灰狼算法和改进灰狼算法寻优的曲线如图4 所示。

图4 灰狼和改进灰狼算法寻优曲线图Fig.4 Optimization curve of grey wolf and improved grey wolf algorithm

由图4 可知：灰狼算法在第5 次迭代时，适应度函数值达到最优值； 改进灰狼算法在第7 次迭代时，适应度函数达到最优值。

改进灰狼算法得到的最优值明显好于灰狼算法的最优值。由此可得，改进灰狼算法明显改进了灰狼算法所存在的提前寻优停滞问题， 同时具有较好的寻优性能。

表2 为经验试凑法、 灰狼算法和改进灰狼算法整定后得到的控制器参数。

表2 控制器参数Table 2 Controller parameter

图5 为风速波形图。

图5 风速波形图Fig.5 Waveform of wind speed

将图5 所示的大于额定风速时的风速输入系统，并将以上3 组控制器参数应用于风电机组变桨距自抗扰控制器中，得到图6，7 所示的响应曲线。

图6 功率响应曲线对比图Fig.6 Power response curve comparison chart

图7 桨距角响应曲线图Fig.7 Pitch angle response curve chart

由图6 可知， 相比于未整定ADRC 参数，经灰狼算法整定的ADRC 参数的功率响应曲线波动范围更小，能更快地稳定于额定功率值附近。

由图7 可知：3 种控制下的桨距角响应曲线基本一致，但从放大图中可以看出明显的差异；当5 s 风速为12 m/s，ADRC 参数未整定时， 风机桨距角为4.8°，经灰狼算法整定参数后风机桨距角为5°，而经改进灰狼算法整定ADRC 参数后的桨距角为5.1°。 当风速大于额定风速时，桨距角的细微变化对风力发电系统有较大的影响，因此，经改进灰狼算法整定ADRC 参数后的风机桨距角精确性更好。

5 结论

本文首先阐述了自抗扰控制器在风电机组变桨控制系统中的作用， 其次阐述了灰狼算法的基本原理及其优化步骤。 由于灰狼算法存在位置更新不完善的问题， 容易延长捕猎时间以及使算法陷入局部最优， 本文提出了利用粒子群算法对灰狼位置更新过程进行改进， 并应用于变桨距控制中，得到以下结论。

①针对灰狼算法位置更新存在的问题， 利用粒子群算法对灰狼个体的移动速度及移动位置做出了改进。

②将改进后的灰狼算法应用到自抗扰控制器中，通过自寻优得到合适的参数值。

③通过在大于额定风速情况下的系统仿真研究， 发现改进灰狼算法能较好地解决自抗扰控制器的参数整定问题， 且自抗扰控制器的参数经过整定后，具有较好的响应速度及抗干扰性能。