我国恶性肿瘤死亡人数比重预测的ARIMA模型*

邓卓,苏秉华,张凯

519088 广东 珠海，北京理工大学珠海学院 光电成像技术与系统教育部重点实验室(邓卓、苏秉华、张凯)；100081 北京，北京理工大学 光电学院(邓卓、苏秉华)

在如今谈癌色变的科技时代，因癌症而引起的死亡病例明显上升，癌症时刻威胁着人类的生命安全[1-2]。恶性肿瘤是全球人类第三大死因。世界卫生组织2002年统计资料表明，全球恶性肿瘤新发病例1 090万，死亡人数670万，现患人数2 460万[3]。2005年统计恶性肿瘤死亡人数已经上升到760万。全球因恶性肿瘤死亡的人数已占总死亡人数的12%，20年后全球每年死于恶性肿瘤的人数将达到1 000万，每年新增人数达1 500万。所以对恶性肿瘤的研究与预测具有十分重要的现实意义[4]。

随着科学技术的发展，将科学技术手段应用于医疗领域，不仅可以更加有效地提高医疗手段，而且可以预测并进一步分析实际出现的问题[5]。在如今的大数据时代，合理地将数据分析方法应用于医疗领域是提高医疗水平的一种方法[6]。本项目将国家统计局官网公布的实际数据应用于差分整合移动平均自回归模型(autoregressive integrated moving average,ARIMA)模型，可以短期预测数据动态。希望可以应用于实际，为我国医疗科技做出贡献。

其中ARIMA是一种时间序列预测模型[7]。模型要求待预测的数据具有一定的平稳性，即样本的时间序列曲线具有形态“惯性”，序列的均值和方差不发生明显变化[8]。ARIMA模型简单，只需要内生变量而不需要借助其他外生变量。

1 材料与方法

1.1 材料来源

本项目采用国家统计局公布于国家数据网上的年度数据中，我国城市与农村恶性肿瘤死亡人数占比的1999年到2017年数据为实验样本，其中利用1999年到2015年数据为实验训练样本，并利用训练好的模型预测2016到2017年数据，并与真实值进行对比，检验模型精准度。所采用的数据如表1所示。对数据进行可视化处理后，其结果如图1所示。

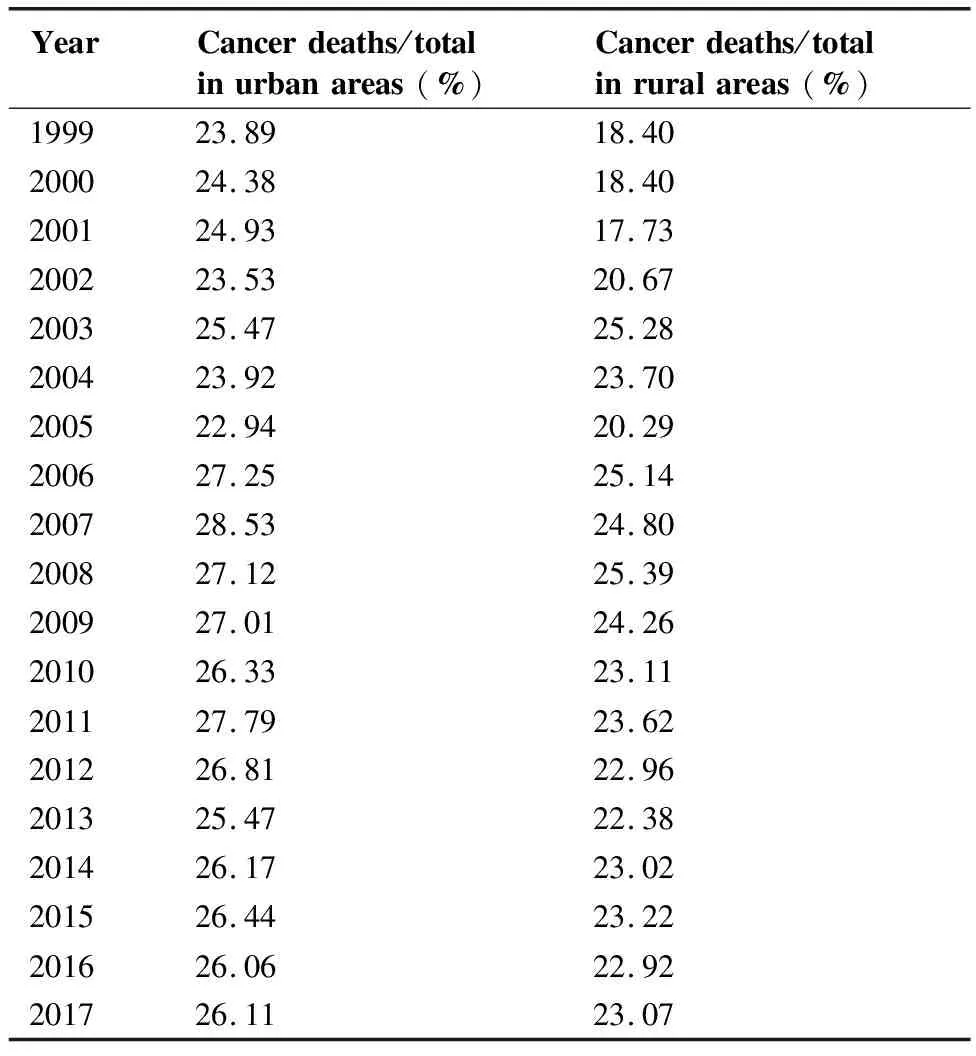
表1 我国城市与农村恶性肿瘤死亡人数占比

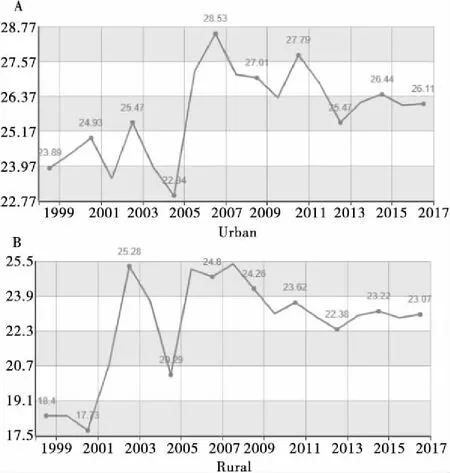
图1 国家数据官网的数据折线图

1.2 模型方法

ARIMA主要由自回归(autoregressive,AR)模型、移动平均(moving average,MA)模型和差分三部分构成[9]。其中AR模型是描述当前时间的值与历史时间的值之间存在的关系，并且利用变量自身历史时间上的数据对自身当前及之后时间值进行预测[10]，p阶自回归过程的数学公式如下：

(1)

这里yt是时间序列的预测值；μ是常数项；εt是被假设为平均数等于0，标准差为恒值的随机误差值；ri是自相关系数。

MA模型通过对自回归模型中误差项累计的移动平均，有效地消除预测中出现的随机波动[11]。提高模型的鲁棒性。模型的数学定义公式如下：

(2)

其中yt是时间序列的预测值；μ是常数项；εt是被假设为平均数等于0，标准差为恒值的随机误差值；θi是MA公式的相关系数。差分法是在时间序列上求t与t-1时刻的差值，使用差分法可以有效使数据满足平稳性。差分运算具有很强的确定信息提取能力，许多非平稳的序列经过差分后显示出平稳序列的性质[12]。经过上述三种方式的综合运用得出模型ARIMA(p,d,q)，其中模型中的参数q由自相关函数(autocorrelation functionl,ACF)图可以得到，表明t时刻的数据受到t-i时刻之间的数据影响；参数d是模型的差分阶数，目的是使数据平稳化，更好地提取数据特征；模型中的参数p为自回归阶数，由偏自相关函数(partial autocorrelation fanction,PACF)图获得。PACF图是剔除了中间k-1个随机变量x(t-1)、x(t-2)、……x(t-k+1)的干扰之后，x(t-k)对x(t)单纯影响的相关程度。ARIMA(p,d,q)模型实际上就是将时间序列上非平稳数据转换成时间序列上平稳的数据，然后将时间变量对数据的滞后值以及随机误差项进行回归预测[13]。模型的数学定义如下:

(3)

其中yt是时间序列的预测值；μ是常数项；εt是被假设为平均数等于0，标准差为恒值的随机误差值，ri是自相关系数，θi是MA公式的相关系数。

从本文实验数据的图示中可看出，两条数据线均不够稳定，因此需要对数据做差分处理。取训练集数据，即1999年至2015年数据做1阶差分处理后基本达到弱平稳状态(图2)。因此模型d参数可确定为数值1。

图2 城市/农村数据1阶差分图

一阶差分处理后的数据的ACF反映了同一序列在不同时序的取值之间的相关性。ACF的数学表达式如下:

(4)

这里，分子是当前时间t与之前时间t-k序列数据的协方差值，分母是当前时间样本方差值。ACF取值范围为-1到1，说明了该函数对该时间序列不同时间点的取值之间的相关性程度。通过ACF图可以确定模型的参数q值，如图3所示。横轴表示滞后时间(年)，深色区间为置信区间，当滞后数据落在深色区域内，表示数据自相关数落到了95%的置信区间。因此只要数据落到置信区间内均可行。从图可知，q值均可取大于等于零的任意值。

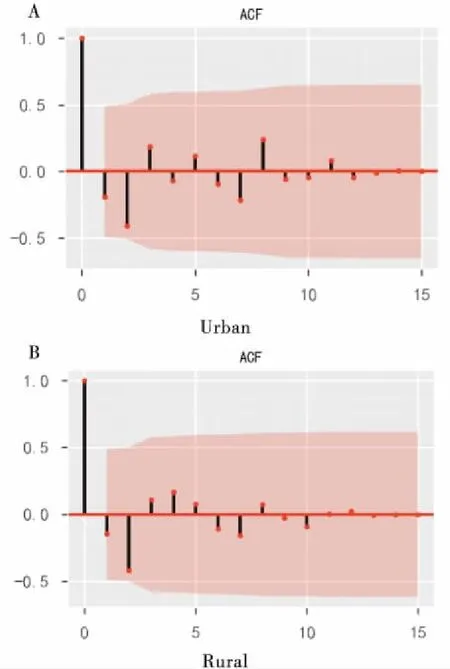
图3 城市/农村数据ACF图

PACF是消除干扰后，恶性肿瘤死亡百分比数据的时间序列与先前时间序列之间的相关性。通过PACF图可以确定模型的参数p值，如图4所示。参数取值原理类似ACF，由于实际具有很多不确定因素，因此只要大部分数据均落在置信区间则可行，由图可知，p值均可取大于等于零的任意值。

图4 城市/农村数据PACF图

为了使模型的参数取值尽量拟合原始数据曲线，且尽量避免出现过拟合现象。选取合适的参数可以提高模型泛化能力。因此利用赤池信息准则(Akaike information criterion,AIC)来选取模型参数可以进一步优化模型。AIC是权衡模型复杂度和拟合优良性的一种标准[14]。判别方法如下：

AIC=2k=2ln(2L)

(5)

其中k是参数的个数，L是似函数。因此AIC值越小参数越合理。通过分析数据的AIC热度图，如图5所示，横轴表示MA模型参数q的取值从0到3，纵轴表示AR模型参数p的取值从0到4。颜色越深AIC值越小，因此由图可以选出模型最优参数。

图5 城市/农村数据AIC图

综上，城市模型取ARIMA(2，1，0)，农村模型取ARIMA(2，1，0)可以使预测模型复杂度低，且可实现较好的实际时间序列情况模拟。

2 结 果

2.1 模型残差正态分布图

为了诊断模型残差序列是否为白噪声，即验证序列中有用的信息是否已被提取完毕。选取模型残差分布图分析模型合理性[15]。如图6所示，模型的拟合残差以0为中心，平均散布在被拟合值点附近，并且在整个拟合范围内具有大致恒定均匀的扩散。因此模型残差符合建模要求。

图6 城市/农村数据残差图

2.2 模型Q-Q图

Q-Q图反映了样本的分布，若样本的散点图在直线y=x附近分布，则样本符合正态分布[16]。本项目中数据经过1阶差分处理后Q-Q图如图7所示。大致符合实验要求。

图7 城市/农村数据Q-Q图

2.3 模型预测

模型完成后，我们用其对2016年和2017年的恶性肿瘤死亡人数比重数据进行了预测，并与实际值对比，如图8所示，图中红色曲线是实际数据，蓝色是预测的2016到2017年的预测数据。从图可知预测值均接近实际值。

图8 城市/农村恶性肿瘤死亡人数占比预测图

利用已有的2016年和2017年实际值与预测值的差值占实际值的百分比，作为模型预测的误差率值，如表2所示。

表2 实验预测值与真实值对比及模型精确度

3 讨 论

由表2可知，预测最准确的是城镇癌症死亡预测的2017年的预测，误差只有0.027%，几乎接近实际值，而其余预测值的误差率也均小于1%。模型对近两年的预测值都比较准确，且误差率较低。因此本项目训练的模型可以应用于实际预计城市和农村近期的恶性肿瘤死亡人数占比。

由实验数据分析可知，利用ARIMA模型对我国城市与农村恶性肿瘤死亡人数占比的预测误差率均小于1%，模型预测准确率均大于99%，因此模型参数合适，模型预测结果具有科学参考性。

本项目利用我国城市与农村恶性肿瘤死亡人数占比的序列时间数据，进行ARIMA模型训练与参数优化，并验证了模型预测数值的准确性。结果表明，此模型可应用于实际死亡人数占比预测。通过对城市与农村数据的分析，可以实现医疗资源更加合理的分配。通过对模型的预测可以进一步分析实际医疗水平的提升程度与实际出现的各种意外状况。

作者声明：本文全部作者对于研究和撰写的论文出现的不端行为承担相应责任；并承诺论文中涉及的原始图片、数据资料等已按照有关规定保存，可接受核查。

学术不端：本文在初审、返修及出版前均通过中国知网(CNKI)科技期刊学术不端文献检测系统的学术不端检测。

同行评议：经同行专家双盲外审，达到刊发要求。

利益冲突：所有作者均声明不存在利益冲突。

文章版权：本文出版前已与全体作者签署了论文授权书等协议。