大数据背景下《实变函数论》的困境与优化

占青义，谢向东

(1.福建农林大学 计算机与信息学院，福建 福州 350002；2.宁德师范学院 数学系，福建 宁德 352100)

大数据时代已经到来，它深刻影响着人们的日常：扩大人类科学的范围，推动人类知识的增长，引领新的经济繁荣。党的十九大报告明确提出：要推动大数据与实体经济的深度融合[1]。正如大数据领域的权威专家舍恩伯特曾说：“大数据是一种价值观，方法论”。

实变函数论是当今高校数学及有关专业的一门专业核心课程，已经成为现代分析不可缺少的理论基础。然而不幸的是,这门课程的名声似乎欠佳。不少学过实变函数的学生,除了留下“抽象，晦涩，难懂”的印象外，收获不多。一种为分析数学带来如此简化的理论，竟然被当作一种复杂得令人难以理解与接受的东西，这值得我们深思。事实上，实变函数论的课程教学在主要内容的选择与组织，关键定义的比较，主要结论的类比与推广3方面面临现实困难。

一方面,实变函数论的许多概念有一定的抽象性，许多重要结论异常深刻，而为得到这些结论所需要的理论知识准备与推演当然也不简单。因此，问题在于：实变函数论的基本内容应当以何种形式提供给初学者，又以何种方式让学生更好地理解与掌握这些重要的结论，做到举一反三。另一方面，很多定理比较晦涩，不知道其主要含义，应用起来比较困难。为此，作者从特例的角度，对一些经典结论进行说明[2-6]。

据我们所知：无论是测度还是Lebesgue积分的基本概念，都免不了某些复杂的构造过程。这些对于训练有素的分析数学研究者固然不难，但对初学的本科生而言，却令人望而生畏。有关测度与Lebesgue积分的基本结果，其描述也不困难，但具体到如何灵活方便的应用，也有很大的发展空间。

本文就《实变函数论》教学中可能会遇到的问题，结合教学实践，从大数据的角度，探讨一些关键概念与定义的比较，对一些经典定理进行特例分析，使得学生能够较快地进入《实变函数论》的核心领域，事半功倍地掌握这门分析课程。

1 运用大数据技术优化实变函数的内容选择

大数据的核心思想之一是基于对海量数据的挖掘与存贮，分析形成观察，从而推动事物更进一步的发展。现阶段，探索运用大数据技术优化实变函数的教学内容，是时代发展的必然要求。

1.1 主要定义的选择与比较

首先，通过对整个教学环节中所生成的数据进行分析，可以提取学生面临的主要问题，从而有针对性地进行内容选择。实变函数是以集合作为研究对象，在集合上定义测度，再建立了可测函数的概念，从而定义Lebesgue积分。

在集合论中，Cantor三分集合是一个很重要的反例。其构造就很有特色，与其类似的有四分集合。其构造如下：将闭区间[0，1]删去居中的长度为0.25的开区间，剩下两个闭区间，在每个闭区间中，再删去居中的长度为的开区间，如此继续下去。所有永远删不去的点所作成的点集记为E,即为四分集。这两个实例说明：P分集是可以实际构造出来的，同时这种集合是可以用数具体表达的。

在测度论中，外测度与测度是一对很容易被学生混淆的概念。其实，在19世纪最先出现外容度的概念,随后C.Jordan建立了可测集的容度定义[2]，而后在1914年由F.Riesz升华了测度论的思想[3],直接从积分出发，导出了整个测度理论。同时，C.Caratheodory进一步发展了外测度理论，导致了测度的完备化[4]。由此可见：测度与外测度是两个互相关联的概念。简单地说：通过包含一个集合的任意开集的体积的下确界，定义了集合的外测度；通过外测度与Caratheodory条件(满足外测度的可数可加性)[5-6]，定义了一个集合的Lebesgue测度。

可测函数是一个让人费解的定义，其证明更是体现了数学分析的一般思路。这里，主要用到了简单函数，示性函数与一般函数。具体说来，先证明这个结论在简单函数上是否成立，然后推广到示性函数[5]。最后证明在一般函数上该结论是否成立。这在Lebesgue积分的定义过程中，有非常精彩的应用。

1.2 与其他积分学的比较

虽然Lebesgue积分有许多优点，但不能否认，Lebesgue积分本身仍然有不足之处。我们把它与其他经典的积分学，如随机积分，进行比较。

1.Lebesgue积分与Riemann积分的主要区别[7-9]：其一，定义的方式不同，导致了可积函数的类型不同：Lebesgue积分的可积函数的范围扩大，使得可积函数从连续函数推广到可测函数；其二，Lebesgue积分降低了积分与极限交换顺序的条件；其三，Lebesgue积分的可测函数空间是完备的，而Riemann积分的可测函数空间是不完备的。可以看出，Lebesgue积分是Riemann积分的一种推广。

2.Lebesgue积分与随机积分的一些区别[10]：其一，定义的方式不同：前者定义在一般的可积函数空间，而后者定义在概率空间上，且定义方式与Riemann积分类似，因而可积函数的类型也不同。其二，定义的种类不同：前者只有一种定义方式，而根据对随机项的Riemann和的不同定义方式[11-12],后者目前常用的有两种定义：Ito积分与Stratonovich积分。

总之,可在这这些突出问题上，争取有一个较清晰的比较。首先,对于基本概念，简化或者回避一些复杂的构造，尽可能地与Riemann积分进行比较，找出其中的异同点，改善教学过程中学生的感受，提高学生的接受效率。并从教学过程的大数据分析中，得到其他需要强化的知识点。

2 运用大数据技术优化实变函数的主要结论

可以积极利用教学大数据，从多维度优化课程的主要结论，同时可以持续地，实时地为我们提供第一手资料，及时调整教学方式方法。根据学生在线学习时的作业，讨论，提问，资料查询等学习行为大数据，得到了如下一些主要结论的优化方案。

2.1 关键假设不能省略的

命题1.Lebesgue定理中，mE＜+∞的条件不能去掉。

以下这个特例验证了命题1成立。

例1：取函数列

2.2 重积分与累次积分的关系

Fubini定理得到了比Riemann积分论中要求更少的结论。以下一些实例说明Fubini定理在应用上更简便。

Fubini定理有一个推论如下[2]：

命题2.若f（x,y）在Rp+q=Rp+Rq上可积，则

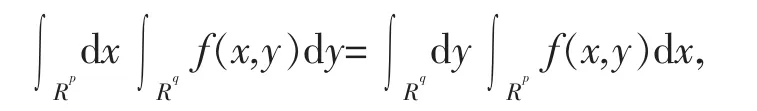
其中,n=p+q，p,q,均为正整数。

命题2的逆否命题同样是真命题。

命题3.若至少有一个不存在,或者都存在但不相等,则f（x,y）在Rp+q=Rp+Rq上积分不存在。

以下例2说明：用命题3验证比用定义验证要更简洁。

例2：如果，x∈（0,1），y∈（0,1）,则f（x,y）在E1={（x,y）;0＜x＜1,0＜y＜1}上是不可积的。

证明：(1)可以用定义证明是不可积的。

事实上，如果令E=（0，1）×（0，1），A1={（x,y）∈E1,,则对任意的（x,y）∈A1,总有。于是可得

因此，f（x,y）在E1上积分无界。同样可以证明：f（x,y）在E1上不可积。这与Fubini定理并不矛盾。

(2)利用命题3很方便验证结论是成立的。其实很容易计算出：

2.3 累次积分的存在与相等，与函数的可积性没有必然联系

命题2的逆命题为：

命题4.若都存在而且相等,则f（x,y）在Rp+q=Rp+Rq上不一定可积。

以下例3说明：函数的累次积分存在且相等，函数有可能是不可积的。

例3：如果

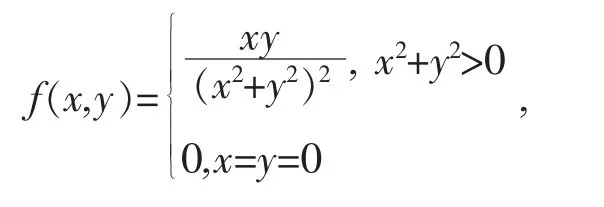
则f（x,y）在E2={（x,y）;-1≤x≤1,-1≤y≤1}上是不可积的，但两个累次积分都存在且相等。

证明：反证。假设f（x,y）在E2上是可积的。则f（x,y）在E2的子集A2=[0,1]×[0,1]上也是可积的。从而应该存在有限积分。但是，当x≠0时，我们可得而函数F（x）在[0,1]上不可积。从而与假设矛盾。

以下例4说明：函数的累次积分存在且相等，函数有可能是可积的。

例4：如果,则f（x,y）在E3=[-1,1]×[-1,1]上是可积的,且两个累次积分都存在且相等。

3 结语

实变函数是现代分析的基础，学生在从古典数学到这种以集合论与测度论为基础的分析学，肯定会遇到很多困难。随着社会经济的不断发展,各种学习形式不断出现。实变函数作为一门古老的理论学科，应该依托大数据技术，通过数据挖据与分析，深入找到自身面临的问题，精准地找到对策。

当前，高校课程大数据建设在数据基础方面还有很大的提升空间，如数据的收集与整理大都依赖人工方式。如何充分利用大数据技术，切实提高实变变函数的教学效果，是教学改革的一项浩大的工程。