一类复值l1范数最小化问题的复值投影神经网络算法
2020-07-23张宋传陆求赐
张宋传,陆求赐
(1.武夷学院 数学与计算机学院,福建 武夷山 354300;2.武夷学院 人文与教师教育学院,福建 武夷山 354300)
考虑一类复值l1范数最小化问题:

其中,A∈Cm×n(m=n),b∈Cm,‖·‖1表示l1范数,使用l1范数最小化旨在提升欠定的线性系统Az=b解的稀疏性。该问题在工程领域较为普遍,以压缩感知领域为例,问题(1)是其一类主要问题[1-2],优化变量z表示未知的稀疏复值信号或图像,或者是原信号在一定稀疏基下的稀疏向量,A=ΦΨ是感知矩阵,其中Φ表示观测矩阵,Ψ表示稀疏基矩阵,b是观测向量,在满足一定条件下,可以通过解问题(1)获得原信号的准确估计值。
当问题(1)退化为实值时,该问题等价于一个线性规划问题,通过凸优化方法可获得精确解。此外,一些快速有效的算法也相继提出,例如神经动力学算法[1]、迫近方法[3]以及Bregman方法[4]等。这其中,只有一小部分算法可以直接用于问题(1),即复值情形的求解,如正交匹配追踪算法(OMP)[5],谱投影梯度算法SPGL1[6],还有一些算法需要采用一些实数化策略,例如,将问题(1)中复数拆分为实部和虚部,将原问题转化为实值问题[7]求解。
递归神经网络算法是一种新型的优化算法,以其内在动力学和并行计算的特征,在过去数十年,被广泛的研究,旨在解决科学及工程领域领域中的出现的大规模实时优化问题[8-9]。文献[1]基于投影算子和投影矩阵,提出了一单层的连续时间投影神经网络算法求解问题(1)的实值情形,并在理论上证明了该网络的稳定性和全局收敛性,基于前向欧拉离散化方法,进一步给出了数值模拟时该网络的离散化算法PNNSR,PNNSR算法不仅保持了连续时间算法的稳定性和全局收敛性,还具有大步长的特性。
但PNNSR算法不能直接用于问题(1)的求解。本文通过定义新的投影函数,提出了一种连续时间的复值投影神经网络模型及其离散化算法(CPNNSR),并在理论上给出了新模型及其离散化算法的稳定性和全局收敛性。新模型及其离散化算法能完全在复域上求解问题(1),同时保留了原有实值算法模型复杂度低,收敛速度快的优点。数值实验进一步表明新模型的离散化算法能有效地求解基于范数最小化的复值稀疏信号的重构问题。
本文中,用Cm×n与Rm×n分别表示m×n复矩阵集与实矩阵集,分别表示矩阵或向量的转置,共轭及共轭转置,Re(·)Im(·)分别表示复值对象的实部和虚部。我们始终假设可行集{z∈Cn:A z=b}非空,且A是行满秩的,则AAH可逆。
1 预备知识
微分是研究复值优化问题的重要理论工具之一[10],微分也称Wirtinger微分[11],或者Brandwood的微分[12],习惯上,我们把传统的复变函数微分理论称为C-微分,二者统称CR微分[10]。
定义1.1[10]设函数g(z):Cn→C,g(z)关于z与z的R导数与导数分别定义为:

定义1.2[10]设函数g(z):D⊆Cn→C,设u是D的一个内点,如果存在u的一个球邻域B(u),B(u)中任一点的R导数与导数都存在,并且R导数与导数在u上连续,则称函数g(z)在u上是R可微的;如果D是Cn中的开子集,函数g(z)在D上任一点上都R可微,则称g(z)在D上是R可微的。
定义1.3[10]设g(z):D⊆Cn→R是R可微的,g(z)的复梯度定义为:。
定义1.4[13]对于任何凸函数g(z):Cn→R,函数g关于z的次微分定义为:
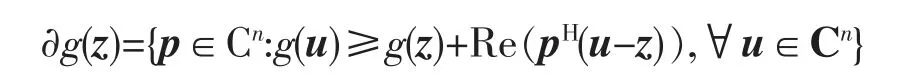
其中,p称为g在z上的次梯度,记˜▽g(z),g在z处的次梯度集即g在z处的次微分。当g可微时,p的唯一可能选择是▽g(z),次梯度即为梯度。
2 新模型及其离散化算法CPNNSR
本文提出的求解问题(1)的复值连续时间投影神经网络模型的动力学方程描述如下:

其中,z∈Cn是状态向量,u∈Cn是输出向量,投影矩阵P=AH(AAH)-1A,易知P2=P,q=AH(AAH)-1b,I是n阶单位阵,参数ε>0,投影函数φ(z):Cn→Ω⊂Cn定义如下:
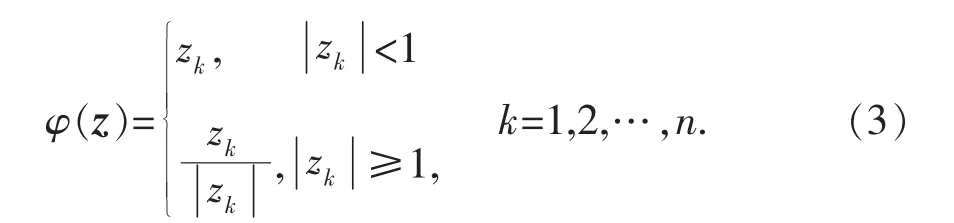
通过前向欧拉离散化方法,得到上述连续时间复值投影神经网络模型的离散化算法:
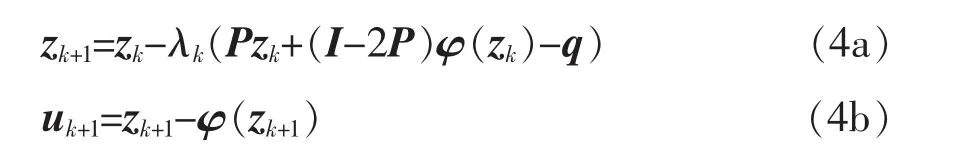
其中,λk是步长,实际应用中,步长λk恒置为1。算法(4)进一步优化为:

本文提出的连续时间的复值投影神经网络模型及其离散化算法(CPNNSR)在结构上类似于文献[1]的实值网络模型及其离散化算法,最大不同在于投影函数的定义。提出复值网络模型及其离散化算法,通过引入新的投影函数,能完全在复域上求解问题(1),同时又保留了原有实值算法模型复杂度低,收敛速度快的优点。关于新模型及离散化算法的稳定性和收敛性结果将在下一节中给出。
3 主要结果
由于问题(1)的目标函数是可分离的,有:

定理3.1u*∈Cn是l1范数最小化问题(1)的最优解,当且仅当系统(2)存在一个的平衡点z*∈Cn时,使得u*=z*-g(z*)。
证明:众所周知,u*∈Cn是问题(1)的最优解当且仅当存在γ*∈∂(‖u*‖1)和ω∈Cm,使得

由引理3.2,γ*=φ(γ*+u*),令z*=γ*+u*,则γ*=φ(z*),u*=z*-φ(z*)。
(5)式两边同时乘以(AAH)-1A,得:

将(7)式代入(5)式,即得:

(6)式两边同时乘以(AAH)-1,有Pu*=q,即:P(z*-φ(z*))=q。结合(8)式,可得

故z*是系统(2)的平衡点。
另一方面,如果z*是系统(2)的一个平衡点,u*=z*-φ(z*),则有:
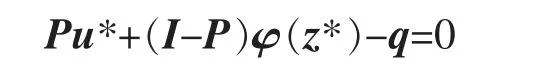
成立。上式两边同乘投影矩阵P,由投影矩阵性质,有P2=P,Pq=q,得:
(I-P)φ(z*)=0,
进而

(9)式两边同时左乘A,有Au*=b。∀u∈{z∈Cn:Az=b},由(10)式,我们有

因为Pu=Pu*=q,进而有

设γ*=φ(z*),因为u*=z*-φ(z*),有γ*=φ(γ*+u*),故γ*∈∂(‖u*‖1)。由定义1.4,‖u‖1-‖u*‖1≥Re((u-u*)Hγ*),由(11)式得,‖u‖1≥‖u*‖1,即u*是问题(1)的最优解,证毕。
最后,给出连续时间复值投影神经网络模型(2)及其离散化算法(4)的稳定性与收敛性结果,其证明与文献[1]类似,出于篇幅考虑,此处略。
定理3.2对任一初始值z0∈Cn,连续时间复值投影神经网络模型(2)中的输出向量u(t)是李雅普诺夫意义下稳定的,并且全局收敛到问题(1)的最优解。
定理3.3对任一初始值z0∈Cn,当0<λk<2时,算法(4)中的输出向量序列{uk}是李雅普诺夫意义下稳定的,并且全局收敛到问题(1)的最优解。
4 数值实验
为了证实算法的性能,本节将运用CPNNSR算法求解基于l1范数最小化的复值稀疏信号的重构问题。实验是在3.40 GHz处理器与8 GB随机存取存储器,Windows 10操作系统下的Matlab R2013b软件上运行的。

图1 各分量的模Fig.1 Modulus of each components
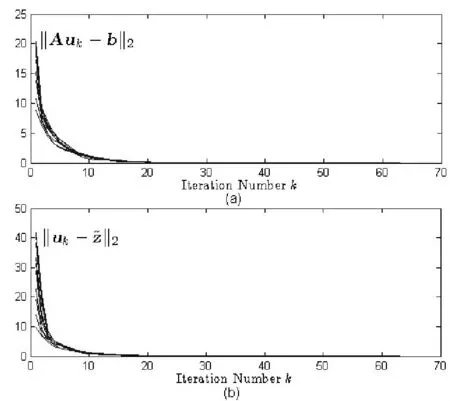
图2 收敛过程Fig.2 Convergence process
