考虑设备劣化及返工的质量批量模型研究

方叶祥，王洪冬，钱 庆，樊树海

(南京工业大学 经济与管理学院，江苏 南京 211816)

经典的经济生产批量(economic manufacturing quantity, EMQ)指的是为了使企业库存得到有效控制而制定的生产批量决策模型。此模型由于假设条件限制，认为设备生产出产品均合格，且认为设备不会发生失效，未能综合考虑反映企业设备实际的运行情况，及生产过程中产品的返工情况，在应用上与实际有较大的差距。为此，本文研究质量需要得到保证，设备维护也需要保证的情况下，批量模型的计算方法。并将这种情形下的批量称为质量批量。

近年来，有很多文献从不同的视角对经济生产批量的决策来进行研究。有部分学者从设备维护及质量来补充经济生产批量模型。如Giri等[1]考虑了随机的故障停机时间和维修时间，运用净现值方法建立了设备维修和EPQ的整合费用模型，并给出了精确的算法。Kim等[2]不但考虑设备的故障情况，而且将产品质量的影响引入到整合模型中，总费用模型中考虑了再加工成本。Chen[3]认为设备可生产出不合格品，对不合格品进行重加工，并对设备进行维护。卢震等[4]引入役龄回退因子和等效役龄概念进行动态预防性维修成本、故障维修成本及次品修复成本的构建[5]。文献[6]认为产品质量和设备劣化水平存在函数关系，由生产出的产品质量结合设备劣化水平来构建设备维护模型。文献[7]指出当结束每一次生产批量的制作时，全面检验所生产的产品。如果次品率远超规定阈值，则维护设备。

有部分学者结合维护及设备劣化来考虑经济生产批量模型。在对设备劣化及设备维护策略中，大部分的研究假设设备维护后如新。文献[8]研究了在产品需求随机、产品合格率随着设备状态劣化而衰减之间的影响关系。文献[9]研究生产批量计划与设备预防性维护计划集成决策方法。文献[10]考虑了设备劣化引起产品缺陷率增大以及顾客需求波动，利用Gamma过程对上游生产单元的劣化过程进行研究。文献[11]采用非完美预防性视情维修、小修与故障更换相结合的维修策略。文献[12]引入性能可靠度约束，以平均费用率最小为目标进行维护。文献[13]考虑产品质量损失和两台设备的缓冲区，寻求最优维护策略。文献[14]将生产批量、质量阈值以及预防性维护阈值联合起来考虑，构造了费用成本模型。文献[15]提出一种加速劣化模型,研究了加速劣化系统的最优视情维修策略。文献[16]运用随机系数增长来刻画变化的设备状态，由经济生产批量和监测的设备状态建立模型。文献[17]研究将离散制造业生产计划问题与生产设备的非周期预防性维修相结合，优化确定最优的生产计划及设备预防性维修序列。

以上研究局限在某个时间点的决策，但在实际制定生产批量决策时，需要从全流程的视角来考虑加工成本问题，追求最大边际效益，需要考虑到返工产品的边际成本。因此，本文考虑设备生产的返工产品成本的边际效应下的期望利润最大值，以探讨实际生产设备劣化及产品返工情况下的生产批量决策(质量批量决策)，为企业制定切实有效的生产批量，获得最大期望利润提供参考。

1 模型描述

1.1 生产设备

在一个生产过程当中，以生产速率为M生产某种产品。设一个生产批量为Q(决策变量之一)，设备在运行的过程中会逐渐发生劣化。本文采用Gamma过程来描绘设备的随机劣化路径。由于此过程具有递增、增量平稳的特性，所以可用来描述设备劣化过程的多种情形，如磨损、腐蚀、钝化等[14]。设生产设备在时刻t的劣化量为X(t)且设X(0)=0，设备的劣化预警点设为V2。其中，劣化预警点是指设备运行到劣化量或设备使用寿命警界点。

1.2 不完全维护策略

设备在生产运行过程当中，为保证设备运行的可靠性，降低设备运行的故障风险，通过对设备劣化水平的检测来为预防性维护提供决策支撑。因某些设备监测数据技术的原因，需设备停机后进行检测。因此，在生产结束后检测设备。设预防性维护的阈值为V1(决策变量之二)，当设备劣化水平X(t)≥V1时，假设设备可以继续进行生产。本文假设维护是不完全的，即使进行了维护，而设备亦不能恢复如新。

1.3 质量控制策略

随着设备的持续运行，设备是处于不断劣化的过程当中，而产品的质量也不断地降低，引用文献[4]中假设次品率是服从幂指数分布φ(t)=β1tγ,γ＞0,0＜φ＜1。其中，为了区分Gamma分布参数中的β，此处系数设为β1。次品数如下：

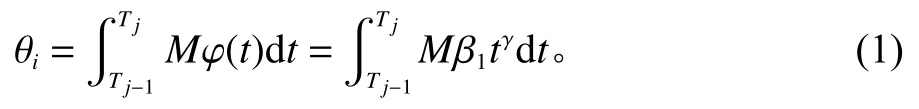
其中，β是设备次品率，γ是次品率系数。

经过不完全的预防性维修，设备的性能恢复得到了改善，运用等效役龄的方法，设备的次品率同设备失效率一样有如下变化。设T为生产周期，N为次数，αi指的是经过i次预防性维修后，改善设备性能的役龄因子，其中0＜αi＜1。

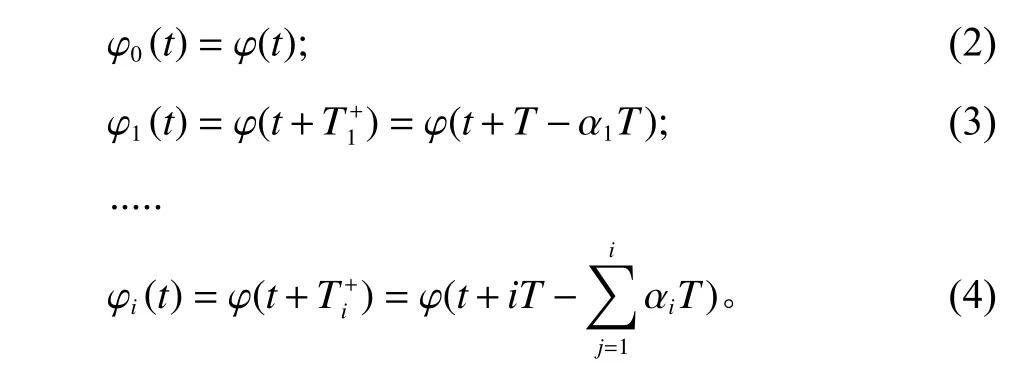
在(0，T)时间内，设备产生的次品数量

在(T，2T)时间内，设备产生的次品数量

在[(N−1)T，NT]时间内，设备产生的次品数量

在生产过程中，加工完的产品立即接受质量检测，而检测出的次品中又存在着可返工产品，可返工产品经过规定的流程返工可获得一定的利益，即要使得所生产获得利益最大化，但是返工次数不可能无休止地进行，所以返工率到达质量控制阈值R(决策变量之三)时，进行预防性更换。

1.4 符号与假设

1) 假设生产过程是持续不断的。

2) 生产设备为单设备。生产过程包括质量批量生产和返工生产2个环节，分别在2台不同的设备上。

3) 进行预防性维护或预防性更换活动后，设备的开机时间忽略。

4) 假设设备劣化值在(0，1)之间。

2 模型构建

cn为预防性维护所需的费用，cm为预防性更换所需的费用。cs为设备启动费用，ca为设备检测费用，ch为单位生产次品的损失。假设Q(t)为[0,t]内生产批量总数。第n个生产批量期为第n个批量与第n+1个批量之间的时间间隔。记Pn为第n个生产批量期内产生的总利润(1≤n≤N(t))，其包括生产产品获取的利润Pn，设备开始的启动费cs、残废品损失DCn、返工成本TCC，以及可能存在的设备检测费用ca、预防维护费用cn、预防更换费用cm。记tn为第n个生产批量开始的时刻，∆=Q/M作为一个批量的生产时间。根据设备的随机劣化行为，第n个生产批量对应有3个互斥的随机事件 {Ai|i=1,2,3}，{A1}表示批量生产过程中设备未发生故障，返工率未到达质量控制阈值R，且生产批量结束后设备劣化水平X(tn+∆)检 测到的值未达到预防性维护阈值V1，无需维护。{A2}表示在批量生产的过程中设备劣化水平超过预防性维护阈值V1，需进行预防性维护。{A3}表示在批量结束时，劣化水平超过劣化预警点V2时，为了使利润获得最大化，此时可继续进行产品生产活动，此时生产的产品会产生返工，但返工所需的成本不大于所获得利润的时候，可继续生产，维持生产活动持续进行。当返工率达到质量控制阈值R时，需要进行预防性更换。如图1所示。

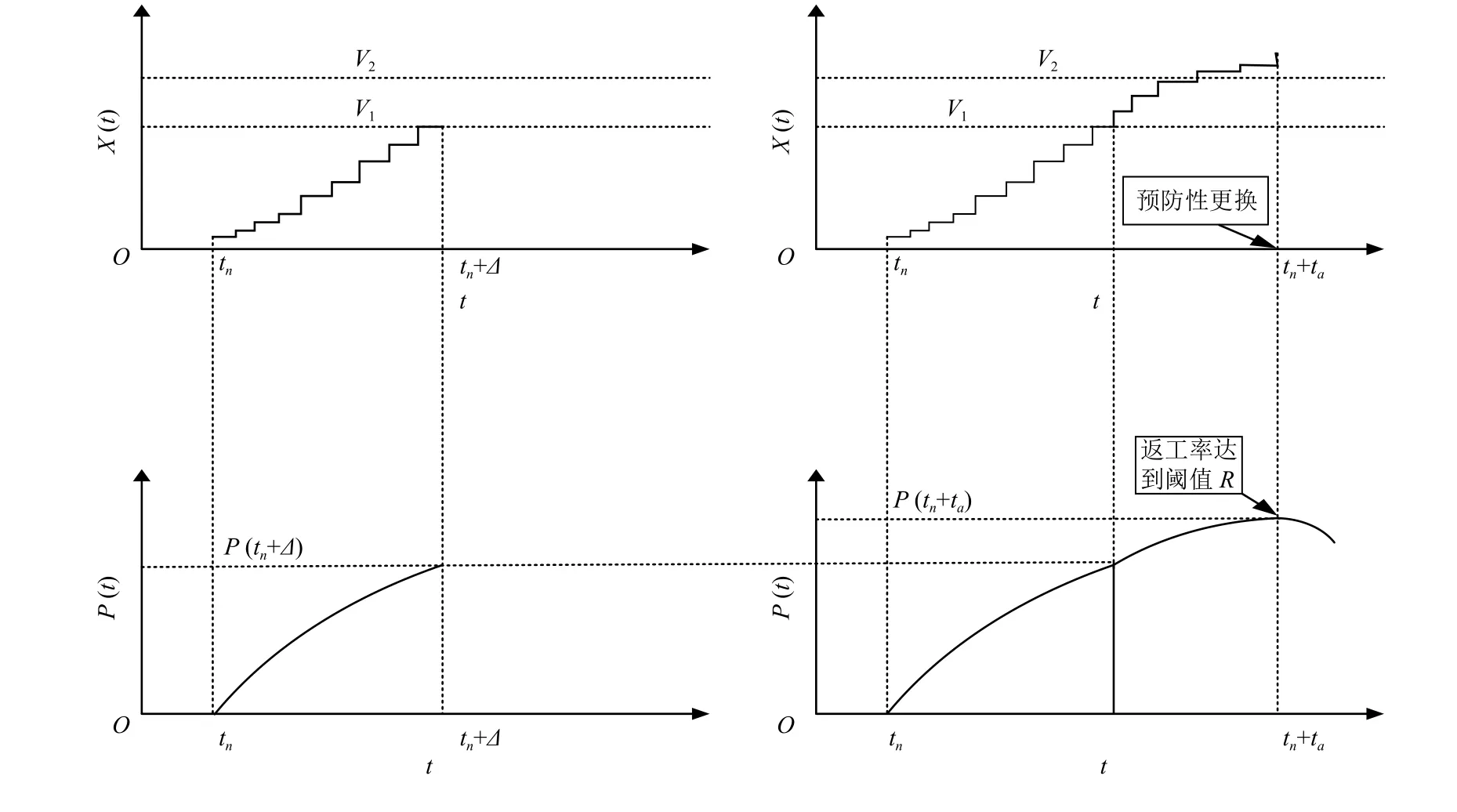
图1 设备在一个生产批量中劣化速率与利润函数变化示意图Figure 1 Schematic diagram of the degradation rate and profit function of a device in a production batch

根据以上3种情形，第n个生产批量期内产生的总利润用Pn可表示为

情形1第n个生产批量结束后设备无需进行预防性维护。

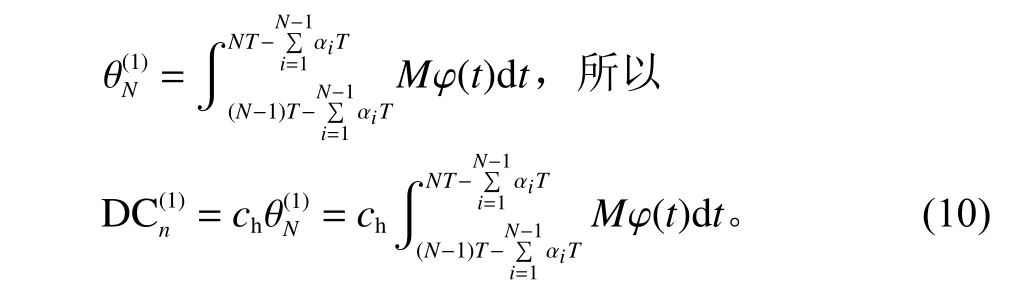
情形2生产过程中设备劣化未达到设备劣化阈值需进行预防性维护。总利润包括：设备启动费用cs、次品损失设备检测费用ca及预防性维护所需的费用cn。

情形3生产过程中返工率达到阈值R需进行预防性更换。

M1—MN表示生产工艺步骤；本文主要考虑返工步骤为2步的工艺步骤，S1为生产工艺的改变原因；S2为上一道工序未达到规定尺寸要求原因；S3为生产材料的更替原因；S4为由于产品检测出问题的原因。设A1、A2为按返工原因进行分类的步骤。返工成本矩阵、返工概率矩阵如表1、表2所示。

返工过程示意图如图2所示。

因此次品返工成本为

表1 返工成本矩阵F(Ai,Sj)表Table 1 Rework cost matrix F(Ai, S j) table

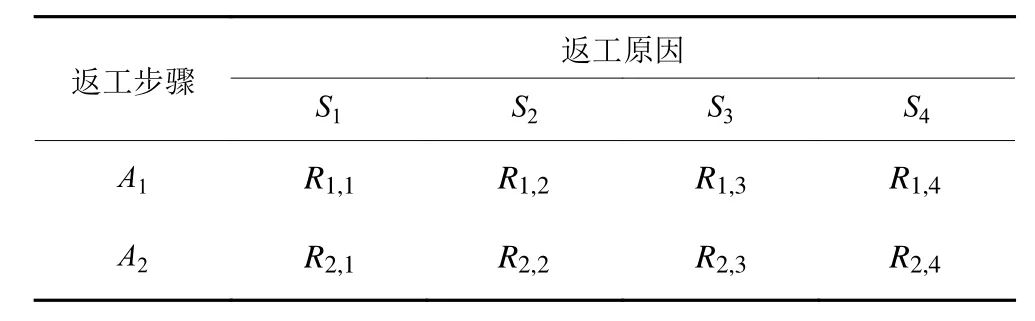
表2 返工概率矩阵R(Ai, S j)表Table 2 Rework probability matrix R(Ai, S j) table

图2 返工示意图Figure 2 Rework diagram

将式(9)、(11)、(13)代入式(8)即可得第n个批量之中的总利润Pn。

记Epn(Q,V1,R)是在设备运行下的总利润期望函数。总期望利润函数等于[0,t]时间内总期望利润即

3 数值实验

设一机床设备对某一固体进行车削加工操作，车削的质量评估标准主要以固体的长度及内径的误差。设M=50 单位/h、cs=800元/次，ca=200 元/次，cm=7 000 元/次，P价=700 元/单位，ch=60 元/单位。根据设备的历史运行数据及供应商所提供数据拟合得：α=0.3，β=0.8(α、β为Gamma分布形参和尺参)，V2=0.95，β1=0.8(幂指数系数)，γ=1.3。

由文献[4]可知，不完全预防性维护的相关变量如表3所示。

求得次品数

表3 不完全预防性维护的相关变量Table 3 Related variables for incomplete preventive maintenance

当设备劣化量小于预防性维护阈值X＜V1时

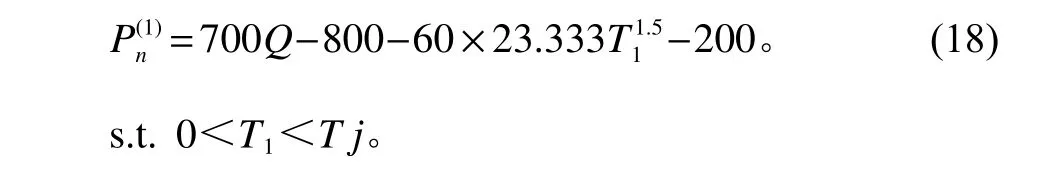
当设备劣化量大于预防性维护阈值X＞V1时

当返工率大于质量控制阈值R(Ai,S j)×θN/Mt≥R时

根据三因素的Box-Behnken的实验方案，采用蒙特卡洛仿真运行17组实验，计算出不同情况下的期望利润对实验记录数据进行仿真500次。再运用Design Expert 8.0.6软件，确定回归方程参数，并绘制出相应的关系图及相关方差分析，如表4。为了研究生产批量大小Q、预防性维护阈值V1、质量控制阈值R对利润的影响，通过方差分析，Q、V1、R对Epn值的效应显著(p＜0.05)。则说明此模型有统计学的意义。失拟项p的值0.842 7＞0.05，则表明无失拟因素存在。二次回归方程如式(21)。

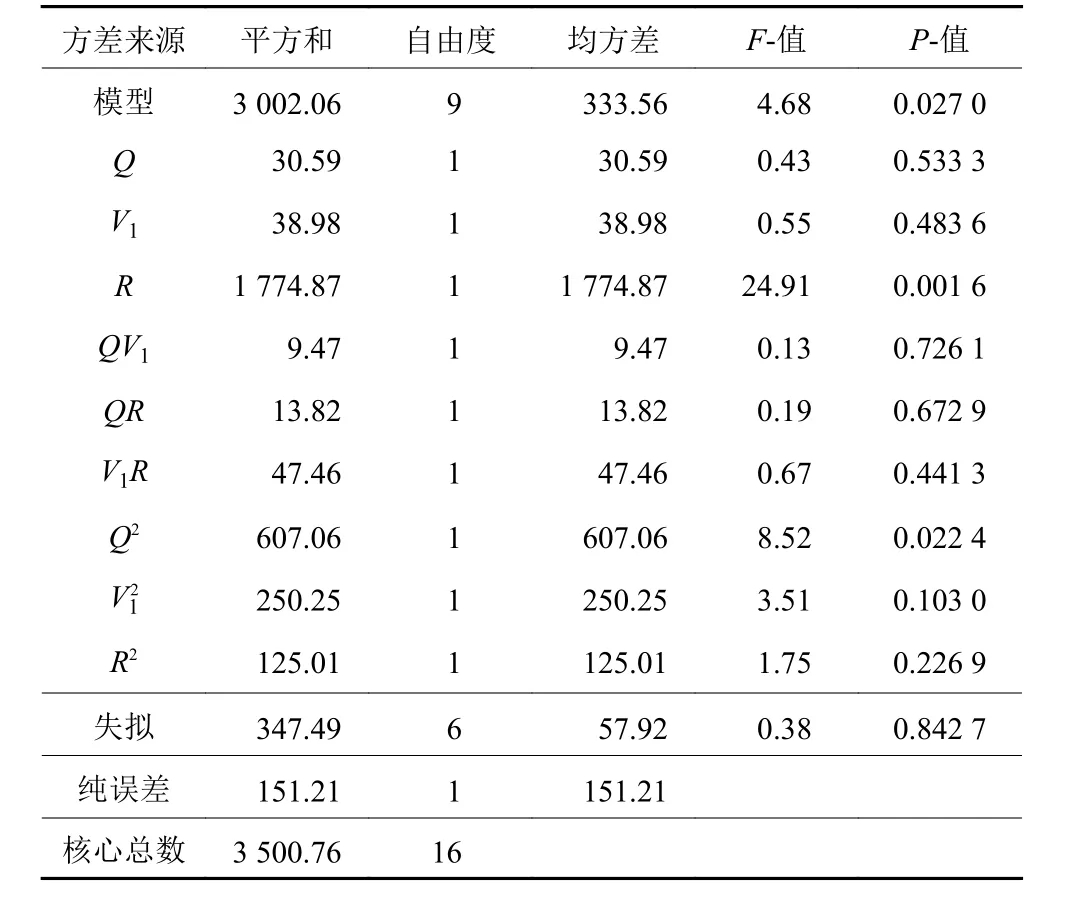
表4 回归系数及方差分析(ANOVA)结果Table 4 Regression coefficient and analysis of variance (ANOVA) results

由图4可知，考虑返工成本近似最优解为(Q*，期望利润值最大Epn=元。因此生产批量为710的时候，若对设备进行检测，其劣化量超过0.70时进行预防性维护。如果返工率达到0.77则对设备进行预防性更换。

图3 未考虑返工成本的拟合所得3个影响因素对期望利润影响的三维曲面Figure 3 Three-dimensional surface that affects the expected profit without considering the rework cost

图4 考虑返工成本的拟合所得3个影响因素对期望利润影响的三维曲面Figure 4 Three-dimensional surface that affects the expected profit with considering the rework cost

综上，考虑边际成本的利润和批量大于未考虑的情况，影响期望利润最重要影响因素是Q，其次是V1，最后是R。

4 结束语

本文主要针对设备的劣化状态、生产批量的大小和维护策略进行联合建模。根据质量控制阈值来对设备进行有效的预防性更换。为了使得生产产品的利润得到更大的提升，通过生产批量、预防维护阈值及质量控制阈值构建决策变量，构造期望利润最大的优化目标模型。通过对比考虑返工成本的边际效应与未考虑的情况下期望利润的最大值，得出考虑返工边际成本的生产批量(即质量批量)能够得到期望利润最大。本文对制造企业的生产管理、设备的维护及提高生产产品的质量，提高生产利润、增加设备的利用率具有一定的参考价值。

本文主要考虑了设备返工成本的边际效应获得最大期望利润。然而，在实际的生产过程中，生产设备由多台设备串联或者并联组合而成，随着设备数量的增加，对于模型的决策变量及求解难度随之上升。对于更复杂的多设备与维护决策的集成问题还需要进一步研究。