基于微分对策的闭环供应链中制造商合作策略选择

张 敏，李思雨，石纯来，廖治通

(1.西华大学 管理学院，四川 成都 610039；2.西南交通大学 经济管理学院，四川 成都 610031)

相比于只存在正向物流的传统供应链，闭环供应链还存在逆向物流[1-3]，在逆向物流中，旧产品被回收商从消费者处回收，然后流向旧产品原制造商处[4-7]。美国人口普查局预测在2 050年时世界人口将达到92.02亿[8]。世界人口的急剧增长使地球资源消耗速度加快，由此产生的环境问题也将威胁到人类的生存。如大量使用矿物燃料导致空气中CO2含量增加，全球气候变暖，海水中N、P含量超标导致海水富营养化等。回收商通过回收旧产品，可以有效地重复利用资源，企业生产成本随资源有效利用率的提高而下降。由于回收再制造的经济性，目前电子、汽车、服装等行业均催生了大量的回收再制造商并获得了成功，如惠普和施乐等公司[9-10]。同时，回收再制造对碳排放的减少也有重要作用，苹果公司由于成熟的回收再制造活动，每单位收益的碳排放量减少15.4%。因此，越来越多国家通过立法促进企业进行回收再制造[11]。加拿大政府对汽车轮胎行业的回收作出了相应的规定，车主更换轮胎时必须提供旧轮胎并支付2.5～7C ＄的回收费用以换取新轮胎[12]。我国也颁布了《废弃电器电子产品回收处理管理条例》以明确制造商对于再制造生产应承担的责任。供应链中处于领导者地位的制造商会选择其他成员合作来提高供应链效率，同时增强其在市场中的竞争力。美国的福特、通用、克莱斯勒公司均与专业的汽车零部件回收商建立合作关系[13]。IBM公司与专业第三方回收公司成立合作联盟[14]。小米与泰国企业VST ECS签订合作合同，负责小米在泰国的分销市场[15]。基于此，部分学者对闭环供应链中成员合作选择策略进行了研究。如，Hong等[16]研究了零售商回收旧产品、制造商和第三方进行再制造模型，并将其与回收外包给第三方的模型进行对比，研究表明当第三方为非盈利组织时，零售商负责回收效果更好。聂佳佳[17]研究了第三方负责回收的情况下，4种不同的供应链成员合作模式的差别，发现闭环供应链中任意两成员间均存在合作动机。Ma等[18]则在此基础上研究了2个回收商负责回收的情况下，制造商的合作策略选择问题，研究发现，制造商与任意回收商合作均使其利润增加。

Hong等[16]、聂佳佳[17]以及Ma等[18]考虑的都是静态模型，而静态模型无法完全刻画现实生活。诸如回收努力投入、批发价格、零售价格、回收价格、需求数量等都是时间的函数，由于没有考虑到长期情况，静态情况下求解所得的供应链最优解只能是短时间内的最优策略，并不是全局最优解。因此闭环供应链系统分析中运用动态模型是必要的。闭环供应链的旧产品回收呈现动态的特征，企业回收努力投入增加，回收率也会呈现逐渐增加的趋势；反之企业回收努力投入减少，回收率的下降趋势与增加相似，呈现渐变的过程。例如企业立即中断回收努力资金，旧产品的回收率不会立即降为零。为了更好地呈现回收率变化的特点，可以将回收率设为状态变量，建立微分方程。同时，动态闭环供应链模型是从长期出发，更加符合实际。基于此，诸多学者研究了动态情况下的闭环供应链中企业战略行为。如黄宗盛等[19]在Savaskan等[9]基础上，对比了微分对策下不同闭环供应链成员回收均衡时利润的大小，在综合考虑经济因素与非经济因素情况下，得出制造商负责回收是最优均衡结果。黄宗盛等[20]又研究了微分对策下第三方回收与集中式决策的差异，发现集中式决策下，产品市场价格较低导致需求较大，整体要优于第三方回收时的均衡结果。何喜军等[21]在Stackelberg博弈下，以企业声誉作为状态变量，通过微分方程求解得出奖惩契约能有效提高企业受益。黄宗盛等[22-23]进一步研究存在竞争性零售商的闭环供应链中制造商的最优决策，认为回收成本系数和转移价格对均衡利润有较大影响。

综上所述，关于闭环供应链中企业合作策略的研究中，如Hong等[16]、聂佳佳[17]以及Ma等[18]，研究均是时间静态模型。黄宗盛等[19-20]、何喜军等[21]以及黄宗盛等[22-23]虽然在时间动态下研究闭环供应链成员策略选择，却忽视了闭环供应链成员互相合作的情况。本文基于上述情况，用微分对策方法研究了闭环供应链中制造商合作策略的选择。具体而言，本文尝试解决如下问题：首先，对制造商是否存在与零售商或回收商合作的可能性进行分析；其次分析不同合作策略下消费者福利的大小；最后探讨了不同合作策略下供应链整体利润大小关系。

1 问题描述

1.1 回收率时间函数

闭环供应链中的回收投入主要包括逆向物流设施建设、对消费者的回收广告宣传、回收人员开销等，用以维持相应的产品回收率。目前关于回收率的模型绝大多数都是时间静态模型[24-25]，是从总体战略角度出发，考虑是否进行旧产品回收以及回收的数量。由于旧产品回收率的变化情况类似于商誉模型中商誉的变化情况，黄宗盛等[19-20]借鉴了Nerlove等[26]的广告商誉模型，本文也借鉴此模型，即

其中，A(t)表示回收努力投入；τ(t)表示回收率；δ表示回收率的衰减系数。回收设施老化，竞争对手加大回收广告投入等都是造成回收率衰减的原因。从式(1)中可以看出，回收率与企业回收努力投入呈正相关关系，随着企业回收努力投入的增加而增加。回收率与衰减系数 δ呈负相关关系，衰减系数 δ较大时，即消费者对企业回收宣传遗忘较快；或企业回收设施老化较快时，企业增大回收努力投入但回收率仍然下降。

1.2 闭环供应链系统的假设

对闭环供应链系统作如下假设。

1) 在闭环供应链中，新材料和回收品同时被用来生产产品。根据Savaskan等[9-10]、Huang等[27]以及Jena等[28]的假设，2种情况下生产出来的产品完全一样，即消费者无法在外观和质量上加以区分[9-10]。制造商使用全新材料生产产品的单位成本为cm，使用回收产品再制造的单位成本为cr，为了保证再制造对制造商有利，令cr＜cm，用∆=cm−cr来表示单位节约成本。如果旧产品由零售商或者回收商回收，制造商需要支付给零售商或者回收商的回收单位价格为b，同时 ∆＞b，否则制造商拒绝回购旧产品。

2) 任意时刻的产品需求函数为D(p(t))=1−p(t)[29]。

3) 制造商、零售商或者回收商的回收成本函数均为C(t)=kA2(t)/2，与黄宗盛等[19-20]的假设一致。其中k为回收成本系数。回收成本随着k值的增大而增大。旧产品回收不仅与企业回收设施的建设、回收广告宣传、回收人员安排等有关，还和消费者的个人素质以及环保意识有关。在一个消费者素质较高且环保意识水平较高的地方开展旧产品回收，回收成本系数较小，反之，则较大。

4) 在供应链系统中，制造商或者含有制造商的合作体为渠道的领导者，其余供应链成员为追随者。

5) 假设任意成员负责回收时，支付给消费者的回收费用为常数 σ。在不失一般性的前提下，设σ=0。这与Savaskan等[10]的假设一致。需要指出的是，即使σ ≠0，也不会改变本文结论，仅增加数学求解的复杂度[10]。

6) 制造商、零售商和回收商的贴现率均为r，决策期为[ 0,∞)。

2 合作策略

企业通过建立合作联盟以实现利润最大化。制造商与谁合作对利润起决定性作用，因此合作联盟十分重要。根据已有的研究[19-20]，零售商、回收商以及制造商的目标函数分别为

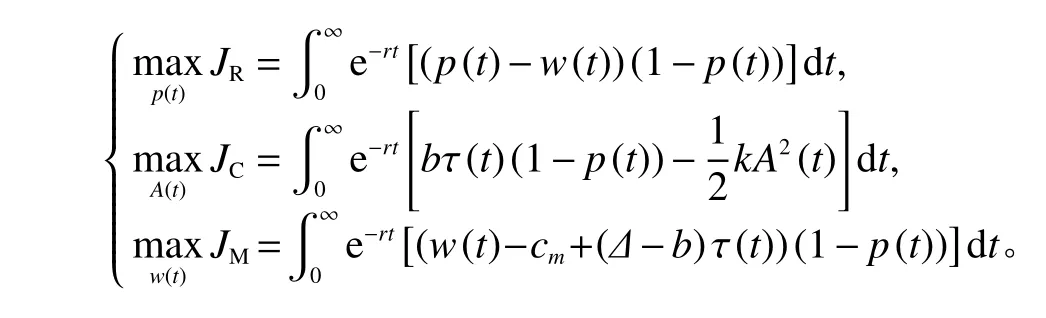
其中，w(t)为产品批发价格。为了保证所有模型中海塞矩阵负定(即存在极大值)和回收率τ ∈(0,1)，令回收成本系数较大k＞k0，其中k0=∆(1+∆−cm)/(4δ(r+δ))，该假设同黄宗盛等[19-20]。

2.1 制造商与零售商和回收商合作模型(Model MCR)

制造商和零售商以及回收商三者合作时，共同决定回收投入A(t)和销售价格p(t)，其目标函数为

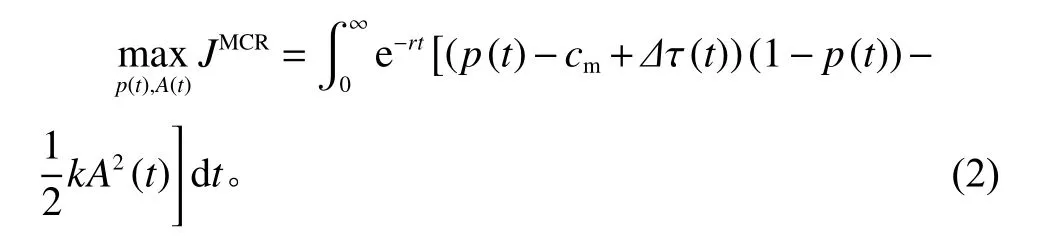
式中，上标MCR表示集中式决策。

命题1制造商与零售商以及回收商三者均合作时，产品的最优零售价格以及最优回收努力投入分别为

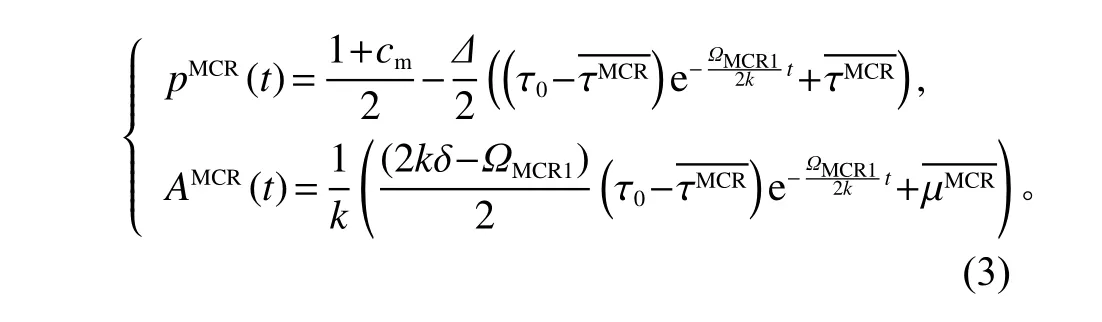
则其最优瞬时利润为

其中，τ0为0时刻回收率以及为均衡回收率为均衡协状态变量。

证明参照Nair等[30]的求解方法，在MCR模型中，整个闭环供应链是一个整体，此时供应链目标是实现整体利润最优，整个闭环供应链共同决定产品零售价格p(t)和回收努力投入A(t)。此时，供应链目标函数为

为书写方便，下文中将省略时间t的书写。即A(t)=A，p(t)=p，τ(t)=τ。

参考最优控制的原理且与黄宗盛等[19-20]一致，构造供应链的现值Hamilton函数为

Nash均衡的必要条件为

µMCR为协状态变量，求解上述方程，由式(7)易解得

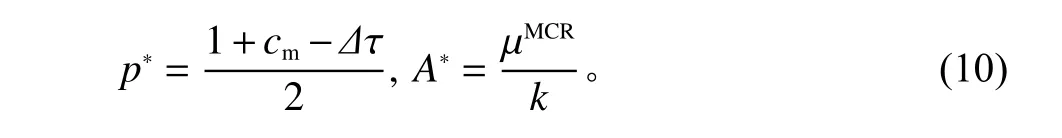
将式(10)代入式(8)和式(9)，化简可得

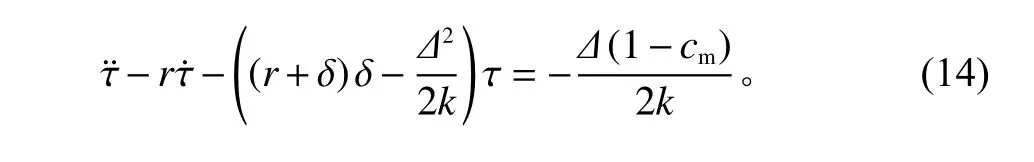
式(11)和式(12)构成一个微分方程组，对式(11)两边同时关于时间t微 分，得=MCR/k−δ，代入式(12)，得

再由式(11)解得µMCR并代入式(13)中，整理得

式(14)为τ 的二阶微分方程，由高等数学微分方程通解可知该方程有一个正的特征根，而仅当另一个特征根应为负时，微分方程的解收敛，故假设两特征根之积为负，即−((r+δ)δ−∆2/2k)＜0。以τ(0)=τ0和为微分方程边界条件，对其进行求解，解得

同理可得

回收率和协状态变量的均衡值为：

将式(17)代入式(10)即可得产品的最优零售价格和最优回收努力投入的表达式

瞬时利润函数式为

将式(18)代入式(19)可得最优瞬时利润

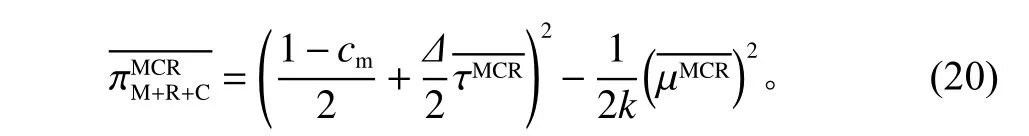
2.2 无合作模型(Model N)

无合作策略下，博弈顺序为：制造商先决定批发价格，然后回收商确定回收率和零售商确定产品价格，通过逆向归纳法得到均衡结果。三者目标函数为

命题2制造商、回收商以及零售商三者均无合作情形下，产品最优零售价格、最优回收努力投入以及最优批发价格分别为

制造商、零售商和回收商的最优瞬时利润分别为

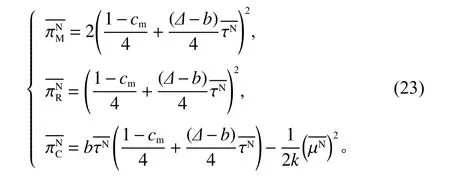
证明与命题1解法相似，故不再详细描述。

2.3 制造商与零售商合作模型(Model MR)

制造商仅和零售商合作，此时二者作为一个整体，目标为合作双方的整体利润最大化。博弈顺序为：首先制造商与零售商决定产品价格，然后回收商决定回收努力投入。其目标函数为

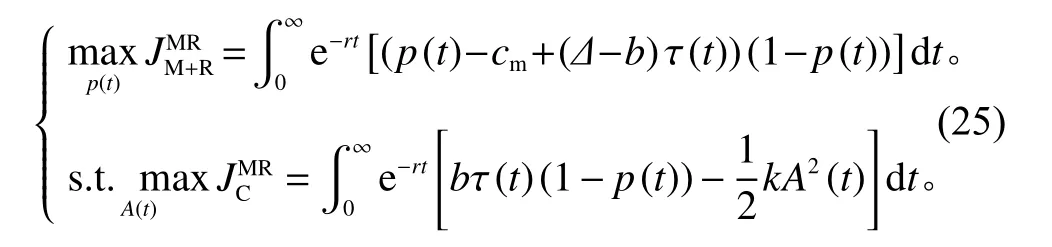
命题3制造商仅与零售商合作情形下，产品最优零售价格以及回收努力投入为

其最优瞬时利润为

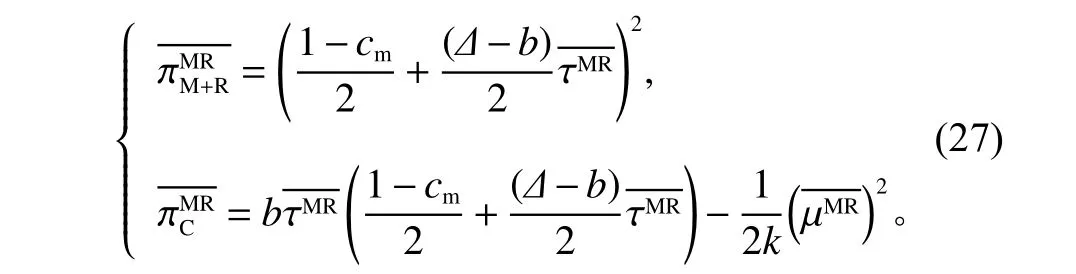
证明与命题1解法相似，故不再详细描述。

2.4 制造商与回收商合作模型(Model MC)

制造商仅与回收商合作时，此时二者作为一个整体，其目标是合作双方的整体利润最大化。其博弈顺序是：首先制造商与回收商共同决定产品批发价格和回收比例，然后零售商决定产品零售价格。其目标函数为

命题4制造商仅与回收商进行合作时，产品最优批发价格、最优零售价格及最优回收努力分别为

其最优瞬时利润为

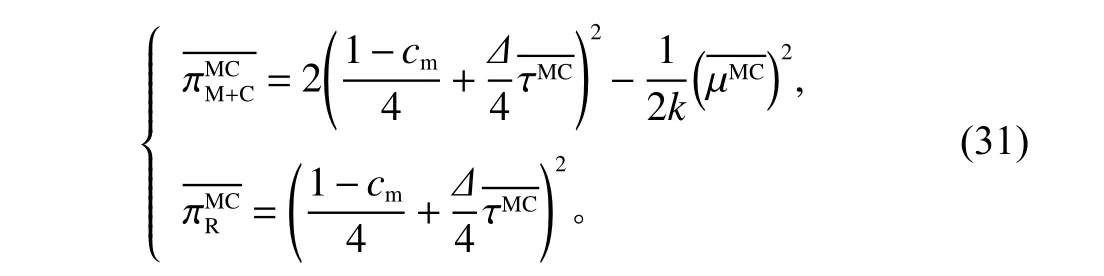
证明与命题1解法相似，故不再详细描述。

3 均衡分析

首先分析不同合作策略下各决策变量的大小关系；其次，探讨制造商是否存在与零售商或回收商合作的可能性；最后探究不同合作策略下消费者剩余和供应链利润大小关系。

命题5不同合作策略下回收努力的大小关系。

1) 若制造商支付给回收商的支付价格较低，即b∈[0,b1]，不同合作策略下回收努力的大小关系为AN＜AMR＜AMC＜AMCR。

2) 若制造商支付给回收商的支付价格较高，即b∈(b1,∆]，不同合作策略下回收努力的大小关系为

证明由A=δτ可知AN、AMR、AMC和AMCR的单调性与τN、τMR、τMC和τMCR的单调性一致，易证上述4种模式中 τ(t)均 为时间t的单调递增函数。若能证明4种模式中的大小关系即可得到τ 的大小关系。已知

易证τMCR最大，τN最小。τMR和τMC大小关系不确定。

由于2kδ(r+δ)−∆2＞0，得是关于b的二次函数，开口向上且有两个根b1和b1′。所以当b∈[0,b1]时从 而τN＜τMR＜τMC＜τMCR。当b∈(b1,∆]时，从而τN＜τMC＜τMR＜τMCR。所以当b∈[0,b1]时，AN＜AMR＜AMC＜AMCR； 当b∈(b1,∆]时，AN＜AMC＜AMR＜AMCR。其中

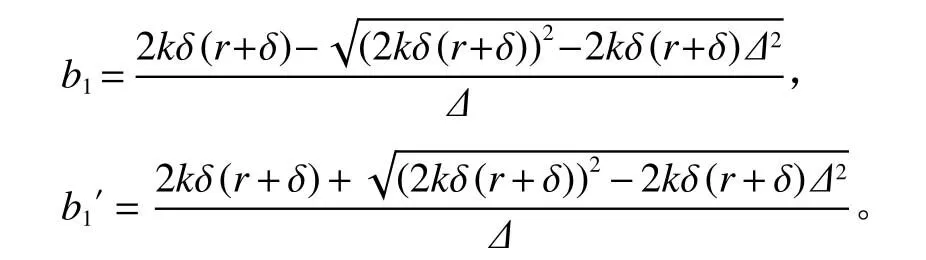
证毕。

命题5说明制造商、零售商及回收商三方合作的策略MCR下回收努力投入最高，均不合作的策略MN下回收努力投入最低。因为在三方合作时，制造商、零售商及回收商为一整体，有共同的利益目标，若三方无合作关系，则均为各自利益进行决策。这会造成极大的负面作用，因此三方都不合作时回收努力投入最低。因为制造商旧产品单位支付b是回收商的收入主要来源，故制造商和零售商合作时：若单位支付b较小，回收商的收益较低，导致回收商的回收努力投入较低；若单位支付b较大，回收商的收益较高，导致回收商的回收努力投入较大。

命题6不同合作策略下零售价格的大小关系为pMCR＜pMR＜pMC＜pN。

证明易证上述4种模式中p(t)均 为时间t的单调递减函数，若能证明4种模式中的大小关系即可得到p的大小关系。已知

命题6说明制造商和零售商以及回收商三方合作的策略MCR的零售价格最低，三方均不合作的策略MN零售价格最高。制造商和零售商合作时，零售价格总低于制造商不和零售商合作时的零售价格，这是因为制造商和零售商合作时总能有效地消除双重边际效应，随之而来降低零售价格。制造商和零售商或回收商合作时的零售价格总高于三方共同合作时的零售价格，因为三方共同合作时有共同的利益目标，能达到薄利多销的局面；总低于三方均不合作时的零售价格，因为均不合作时会存在极大的边际效益，导致零售价格较高。

命题7存在制造商与零售商合作的可能性，即

证明沿用命题5中的证明方法，不同模型中的利润大小可通过比较相对应的瞬时利润得出。将MR模型中制造商与零售商合作利润与N模型中制造商和零售商利润之和作差得

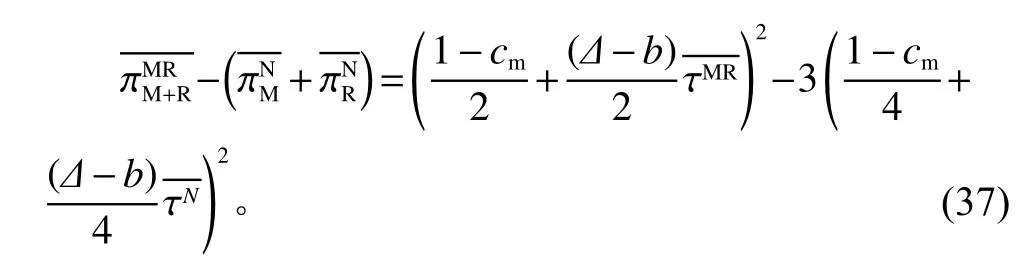
因为τMR＞τN，易知所以制造商与零售商合作。证毕。

命题7说明制造商存在与零售商合作的可能性，因为制造商和零售商合作时，总能有效地消除双重边际效应。制造商和零售商合作后，制造商与零售商为一个整体，无需制造商设定批发价格，零售商的零售价格就可以下降，达到薄利多销的局面，此时制造商和零售商合作的共同利润会大于不合作时各自决策情形下的利润。所以制造商和零售商总存在合作的可能性。

命题8制造商有动机与回收商合作，即

证明沿用命题5中的证明方法，不同模型中的利润大小可通过比较相对应的瞬时利润得出。将MC模型中制造商与回收商合作利润与N模型中制造商和回收商利润之和作差得

式(38)大小由16(δ+r)2((b−∆)δ−2r∆)(b−∆)δ2k2+H0−(2(δ+r)∆2−2bδ∆+b2δ)b2∆2决定。其中

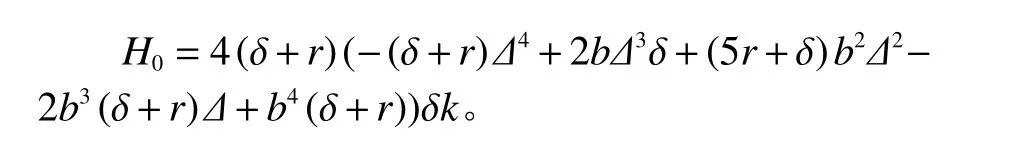
假设上式有两个根k1和k2(令k1＞k2)，当k＞k0时，

将k1和k0作差得

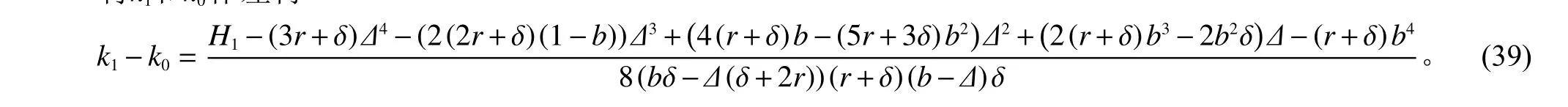
因为b∈(0,∆)，易证仅当b=∆时，k1=k0，当b=0时，k1＜k0，所以在b∈(0,∆)时，k1＜k0。即制造商与回收商合作的可能性总是存在的。若假设不成立，即式(39)只有一个根或者无根，上述命题依旧成立。证毕。

命题8说明制造商总存在与回收商合作的动机。聂佳佳[17]得出在静态环境下，只有在一定条件下制造商才存在与回收商合作的动机。与其不同的是，本文基于动态环境得出制造商总存在与回收商合作的动机。是由于在动态环境下，制造商与回收商合作时，二者作为一个整体，能回收到更多的旧产品进行再制造，制造商生产成本下降更多，制造商主动降低批发价格，零售商因此自发降低零售价格，零售价格的降低又会增加市场需求数量，最终制造商和回收商合作总收益增加，故制造商与回收商合作的动机总是存在。

命题9不同合作策略下消费者剩余的大小关系为C SMCR＞CSMR＞CSMC＞CSN。

证明借助Arya等[31]，易知消费者剩余CS=D2/2，易证上述4种模式中 CS(t)均 是时间t的单调递增函数，若能证明4种模式中 CS的大小关系即可得到 CS的大小关系。已知

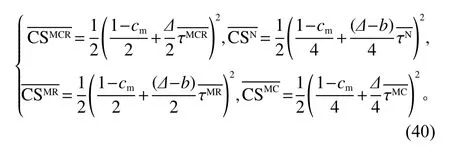
结合命题5中 τMCR最大，τN最小，可知 CSMCR最大，最小。和大小关系不确定。

其大小由(2δ2+2δr)k−∆2+∆b−b2决定。当k＞k0时，即不同合作策略下消费者剩余的大小关系为C SMCR＞CSMR＞CSMC＞CSN。证毕。

命题9说明制造商、零售商和回收商三方都合作时，消费者剩余最大。三方都不合作时，消费者剩余最小。这是因为三方都合作时，均为共同的利润目标努力，此时不存在内耗，销售数量多，回收率最高，生产成本因再制造而降低明显，所以零售价格最低，真正达到薄利多销的局面，因此消费者剩余最大。制造商和零售商合作时，消费者剩余要大于制造商和回收商合作时的消费者剩余，这是因为消费者剩余和销售数量呈正相关关系，制造商和零售商合作能有效消除双重边际效应，产品需求数量大于制造商和回收商合作时的数量，故制造商和零售商合作时消费者剩余较大。

4 算例分析

由于不同模型中的总利润函数过于复杂，本文通过算例分析转移支付b、回收成本系数k以及再制造节约的单位成本 ∆对不同模型中总利润大小的影响。令cm=0.7,r=0.15, δ=0.5, ∆=0.4,k=0.44,b∈(0, 0.4)，可得图1；令cm=0.8,r=0.15,δ=0.5, ∆=0.45,b=0.1,k∈(0.45, 1)，可得图2；令cm=0.8,r=0.15,δ=0.5,k=0.45,b=0.1,∆∈(0.2, 0.45)，可得图3。

由图1、图2和图3可知，供应链总利润在制造商和零售商以及回收商三者合作时最大，三者无合作时最小。制造商仅和零售商合作时与制造商仅和回收商合作的供应链总利润大小关系与转移支付b、回收成本系数k以及再制造节约的单位成本 ∆有关。如图1所示，在回收成本系数及再制造节约的单位成本均适中的情况下，转移支付较小时，回收商利润较小，因为转移支付是回收商利润的唯一来源，此时回收率由于回收商回收努力投入较低而处于较低水平，制造商通过回收再制造获益较小，由回收再制造带来的生产成本降幅也较小，故零售价格较高。尽管制造商和零售商合作的确对整个供应链利润的增加存在促进作用，整体供应链利润的确高于三者无合作时的利润，但是低于制造商与回收商合作时的供应链利润。制造商和回收商合作时，因为并不需要转移支付，供应链整体利润并不受转移支付变化的影响。随着转移支付的增大，回收商利润增加，回收努力投入也随之增大，制造商的生产成本因再制造而大幅度降低，制造商和零售商合作时以较低的价格出售产品，产品销量因此增加，达到薄利多销的共赢局面，制造商和零售商利润增加大于转移支付给回收商回收旧产品的利润，供应链整体利润是增加的。当转移支付大于一定值时，由于成本降低带来的收益增加大于转移支付的费用，从供应链总利润角度出发，此时制造商选择与零售商合作要优于制造商与回收商合作。

由图2可知，在转移支付较小和再制造节约的单位成本适中的情况下，由于回收成本与回收效率是负相关的，随着回收成本系数的增加，回收效率下降，生产成本上升，所有合作策略下的供应链整体利润都随之减少。回收成本系数较小时，制造商和回收商合作时，双方合为一个整体，其回收效率明显大于回收商回收时的效率。双方通过回收再制造获得的利润较之制造商和零售商合作时所减少的双重边际效应的损失而言要大，从供应链总利润角度出发，此时制造商选择与回收商合作要优于制造商与零售商合作。回收成本系数较大时，回收商负责回收下与制造商和回收商作为一个整体来负责回收相比，回收效率差别不明显，均处于较低水平。再制造减少的生产成本较小，而制造商和零售商合作所减少的双重边际效应带来的损失就显得比较大，从供应链总利润角度出发，此时制造商选择与零售商合作要优于制造商与回收商合作。

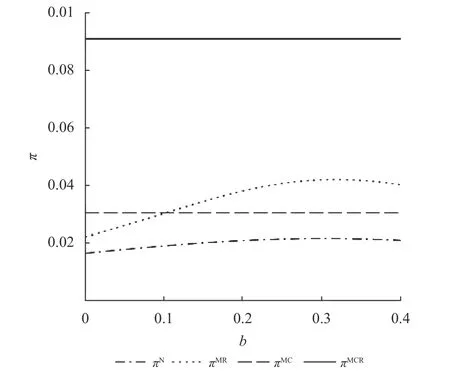
图1 b对供应链利润的影响Figure 1 The impact of b on the profit of the supply chain

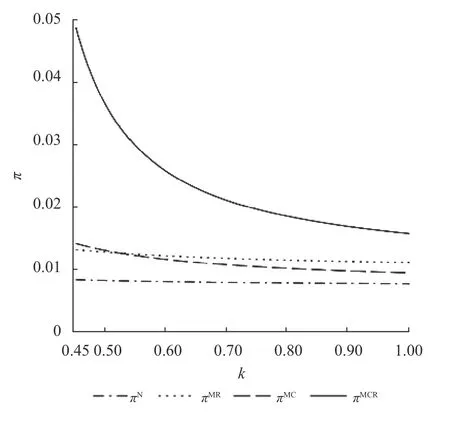
图2 k对供应链利润的影响Figure 2 The impact of k on the profit of the supply chain

图3 ∆对供应链利润的影响Figure 3 The impact of ∆ on the profit of the supply chain

如图3所示，在回收成本系数适中和转移支付较小的情况下，随着再制造节约的单位成本的增加，生产成本降低，所有合作策略下的供应链整体利润都随之增加。当再制造节约的单位成本较小时，产品回收率较小，制造商因再制造节约的成本较小，此时制造商和零售商合作能有效地降低双重边际效应带来的损失，而制造商和回收商合作所节约的利润与之相比则较小，从供应链总利润角度出发，此时制造商选择与零售商合作要优于制造商与回收商合作。由于转移支付较小，而回收商负责回收时，其收入主要由转移支付构成，此时回收商回收努力投入较小导致旧产品回收率也较低，当再制造节约的单位成本较大时，回收再制造能有效降低生产成本从而提高利润。制造商和回收商合作，出于共同目标考虑，能有效提高回收率，因再制造所增加的利润要远大于制造商和零售商之间双重边际效应的损失，从供应链总利润角度出发，此时制造商选择与回收商合作要优于制造商与零售商合作。

5 结论

处于领导者地位的制造商会选择与其他成员合作来提高供应链效率，同时增强其在市场中的竞争力。本文以动态环境为研究背景，研究了供应链中制造商的不同合作策略。首先构建了制造商零售商和回收商共同合作(MCR)、制造商零售商和回收商都不合作(N)、制造商和零售商合作(MR)以及制造商和回收商合作(MC)等4种合作策略，基于微分对策理论，分别计算各策略下最优控制策略并进行分析，探讨制造商与供应链各成员合作的可能性；最后探究不同合作策略下消费者剩余和供应链利润大小关系。得出以下结论。

1) 制造商、零售商和回收商均合作，即三者作为一个整体时，消费者福利最高。

2) 制造商、零售商和回收商都不合作时，即三者独立决策时，产品零售价格最高。

3) 制造商、零售商和回收商均合作时，三者作为一个整体，回收努力最大。制造商、零售商和回收商都不合作时，三者各自决策，回收努力投入最小。制造商和零售商合作以及制造商和回收商合作时回收努力投入大小则与制造商支付给回收商的支付价格有关：(1) 若制造商支付给回收商的支付价格较低，制造商和回收商合作，即二者共同决策时回收努力投入较大；(2) 若制造商支付给回收商的支付价格较高，制造商和零售商合作，即二者共同决策时回收努力投入较大。

4) 制造商和零售商或回收商都存在合作的可能性。

5) 制造商和零售商以及回收商三者合作时的供应链总利润最大，三者无合作时供应链总利润最小。制造商仅和零售商合作时与制造商仅和回收商合作的供应链总利润大小关系与转移支付b、回收成本系数k以及再制造节约的单位成本∆ 有关：(1) 随着转移支付b、回收成本系数k的增大，制造商和零售商合作时供应链利润由先低于变为后高于制造商和回收商合作时供应链利润。(2) 随着再制造节约的单位成本 ∆的增大，制造商和回收商合作时供应链利润由先低于变为后高于制造商和零售商合作时供应链利润。

本文建立的闭环供应链中生产成本假设为固定单位生产成本，而日常生活生产中常出现规模不经济导致单位生产成本递增。因此，未来研究将考虑生产成本递增情况下的合作策略选择问题。其次，本文中假设只有1个制造商、1个零售商和1个回收商，忽视了竞争的情况，进一步研究可以把竞争考虑在内。最后，本文中假设制造商为合作策略制定者，而现实生活中，供应链各成员均有选择合作伙伴的权利，所以接下来的研究可以把零售商和回收商合作考虑在内。