面向时间与能耗的工业机器人运动参数优化

2020-07-22夏绪辉曹建华

机械设计与制造 2020年7期

周博，夏绪辉，王蕾，2，曹建华

（1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北武汉 430081；2.武汉科技大学服务科学与工程研究中心，湖北武汉 430065）

1 引言

工业机器人的运动优化是其控制系统中的基础性研究领域，决定着机器人的运动方式和作业性能。机器人在关节空间运动过程中，其作业时间和作业能耗受到运动参数的影响[1]。目前，相关学者大多是以效率最高或能耗最少为目标对机器人运动参数进行研究。文献[2]建立时间优化模型，其目的是为了在满足相应约束的前提下使运行速度最大，从而缩减机器人总的运动时间。文献[3]考虑关节二次加速度，使用权重分配法建立了时间-二次加速度优化模型，用六关节机器人仿真模拟对该方法进行了验证。文献[4]充分利用机器人的动态性能，通过优化设定点的行程和两点间的具体运行路径，实现在最短时间内完成制造任务。针对机器人能耗最优问题，文献[5]以工业ABB 机器人的各个关节为研究对象，建立其驱动模型，通过优化算法得到了不同工况下的最优能耗轨迹。文献[6]为了使机器人在能量一定时作业时间最长，构建伺服电机能耗模型，通过实验分析计算得到了机器人最小能耗延长了其运行时间。在实际工业生产中，作业时间和作业能耗通常需要同时考虑，针对这一问题，文献[7]使用归一化加权法和平均模糊隶属函数对时间和能耗模型处理得到两种目标函数，采用NSGA-II 算法和MODE 算法寻优求解。文献[8]用三次多项式拟合两点之间的轨迹，采用弹性系数法和加权系数法定义了关于时间和能耗的目标函数，引进一种新颖的罚函数来处理约束问题，为了提高解的质量，提出一种新的算法来对目标函数进行求解。在对能量或效率进行优化时，现有研究考虑了机器人运动的平滑性和冲击，但是当综合考虑能量和效率时，大多采用三次多项式定义机器人在关节空间中相邻两点的轨迹，考虑了各关节在起始点和终止点的位置和速度约束，忽略了加速度约束，这样会使加速度曲线不平滑，引起机器人的振动和冲击，从而加剧零部件的损伤，尽管确定的轨迹有一定平滑性，但是还是会对机器人动力学和惯性载荷产生影响[9]。现有研究在双目标模型转换时，大多采用弹性系数法以消除时间和能耗在数量级上的偏差，这种方法虽然强化了时间在目标函数里的地位，但是时间和能耗两者的灵敏性还是会有很大的差别。

有鉴于此，用五次多项式来拟合给定相邻两点的运动轨迹，结合机器人运动学和动力学方程，建立机器人的时间能耗模型。以时间和能耗作为工业机器人作业过程绿色度的定量指标，定义了每一段轨迹的目标函数。为了便于计算和有效平衡全局搜索和局部搜索，引入增广拉格朗日乘子方法将模型简化，采用带收缩因子的粒子群算法进行求解。对中纤板生产线作业机器人的仿真验证了所建模型的适用性和算法的有效性。

2 运动参数优化问题描述

机器人各个关节从点到点的轨迹一般遵从距离最短原则进行设定，但是在实际运动过程中，由于受到外部环境的影响以及自身工艺参数的限制，机器人只能沿着给定的路径点运行。当给定两点的轨迹时，机器人各个关节在运行过程中，其力矩、速度、加速度和二次加速度会发生相应的变化，这些运动参数会影响机器人在这个过程的作业时间和作业能耗。在对机器人运动参数优化时，假定关节空间的关节路径点已知，空间中无避障，只考虑运动参数对时间和能耗的影响。

2.1 关节轨迹函数

机器人在关节空间中的轨迹是由一系列的路径点组成，利用多项式来拟合点到点的轨迹并不是唯一的。为了防止系统冲击振荡，保证作业过程的平稳性，需要对每一段作业轨迹起始点和终止点的加速度进行限制，所以采用五次多项式来定义机器人在关节空间作业过程中相邻两点的关节轨迹。设机器人第i（1≤i≤N）个关节在第m（1≤m≤L）段轨迹作业过程中经过起始路径点的时刻为tim0，经过终止路径点的时刻为分别为第m段轨迹的关节位移、角速度、角加速度和二次加速度，则机器人第i个关节在第m段轨迹作业过程中起始和终止位置需要满足的相应运动学约束条件如下：

假定关节i在第m段的五次多项式轨迹函数为：

联立式（1）～式（2），求得五次多项式的系数如下：

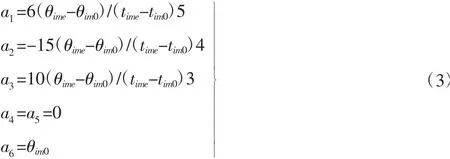
2.2 机器人动力学模型

对于一个具有N个关节的工业机器人机械臂，忽略各关节之间的摩擦力，由拉格朗日-欧拉方程得到关节i所需的广义力矩为：

式中：τ（it）—第个关节的广义力或力矩—角位移、角速度、角加速度；Dij、Dijk、Gi的具体表达式见文献[8]。

2.3 时间与能耗模型

已知机器人第个关节在第m段轨迹作业过程中经过起始点和终止点的时刻分别为tim0、time，则可得第个关节在第段轨迹的作业时间为：

由于机器人所有关节的运动都是同步的，所以机器人在某一段轨迹的运行时间Hm等于其中一个关节在该轨迹的运行时间Him。利用前文中求出的轨迹函数θim（t），结合机器人的关节力矩函数，可以得到机器人在第段轨迹的能耗为：

2.4 目标函数

由于机器人在每一段轨迹里面的运动都是相互独立的，所以可以分别对每一段轨迹进行优化，从而得到时间和能耗平衡的最优机器人运动参数。

考虑工业机器人作业过程的环境友好性，可通过量化计算体系的绿色度来判断作业的绿色性[10]。以时间和能耗作为工业机器人作业过程绿色度的定量指标，以最大化绿色度为目标，建立工业机器人作业路径优化数学模型：

需满足的约束条件：

式中：Hmax、Hmin—一段轨迹里面仅以时间作为优化目标时的最大时间和最小时间；Emax、Emin—一段轨迹里面仅以能耗作为优化目标时的最高能耗和最低能耗；H和E—一段轨迹里面时间和能耗的测度值；viC、aiC、jiC、τiC—关节速度、加速度、二次加速度和力矩的最大值；η1、η2—时间加权系数和能耗加权系数，且η1+η21。η1=1 和η2=1 分别对应于最优时间的运动参数优化和最优能耗的运动参数优化。

对机器人的运行时间和能耗进行系数加权，可以根据实际情况，调整η1和η2的值，使得时间和能耗在一定情况下达到平衡。

3 运动参数优化算法

3.1 带收缩因子的粒子群算法

粒子群算法与其他智能算法相比，具有简单实用，对非线性寻化问题具有良好的全局收敛能力[11]。

假设粒子具有D维搜索空间，第i（1≤i≤n）个粒子第k（1≤k≤MaxDT）次迭代时的位置飞行速度第i个粒子当前所发现的最优位置为当前整个群体所发现的的最优位置为和r2为两个独立的随机数，c1和c2为加速常数。

为了保证PSO 算法的收敛性，引入收缩因子χ：

则相应粒子的速度和位置更新公式为：

其中，取c1=c2=2.05，φ=4.1，所以χ=0.729。因此，该PSO 算法可以称为带收缩因子的粒子群算法[12]（CPSO），它可以有效平衡全局搜索和局部搜索，避免算法陷入局部最优。

3.2 增广拉格朗日乘子（ALM）方法

ALM 方法与惩罚函数方法类似。该方法不需要多次测试来确定初始惩罚因子，惩罚因子也不需要趋于无穷大，但是，在数值稳定性和计算效率方面超过了罚函数法。

利用ALM 方法将不等式约束问题转化为无约束问题：

式中：x=（x1，x2，…，xn）—自变量；G（x）—为目标函数；gj（x）≤0（j=1，2，…l）—第j个不等式约束；λj—第j个拉格朗日乘子；rj—第j个惩罚因子。

在优化过程中，拉格朗日乘子和惩罚因子的迭代更新公式分别如下：

式中：z—第z次更新；εg—约束误差精度。

当z=1 时，终止标准为：

当z=2，3，…zmax时，终止标准为：

式中：ε—收敛精度；zmax—最大更新次数。

3.3 改进型粒子群算法

由于CPSO 算法和ALM 方法各有其独特的优势，所以可以将两种方法结合，利用两者的优点，得到一种新的求解非线性约束问题的方法。针对能耗时间求解最优运动参数问题属于这一类问题。

该算法的主要思想如下，相应的迭代过程，如图1 所示。

图1 算法流程图Fig.1 Algorithm Flowchart

（1）利用ALM 方法将约束问题转化为无约束问题（式10）；

（2）随机产生一组数据作为粒子的初始值；

（3）判断初始输入值是否满足迭代终止标准（式13），如果满足，则输出当前解作为最优解，否则，保存当前获得的最优解，然后提出一个新的无约束问题（式10），应用随机数据产生一组新的粒子，采用CPSO 算法更新粒子的速度和位置，判断是否满足终止标准（式14），然后应用式11 和式12 分别对拉格朗日乘子和惩罚因子进行更新。

（4）通过反复迭代寻优，目标函数的全局最优解可以最终求解出来，同时可以得到最优的运动参数。

4 案例分析

以本项目组开发的某中纤板生产企业的生产线为例，以大型多功能6 关节机器人MotomanHP165 为研究对象来进行仿真验证，用三维软件画出其生产现场三维简图，如图2 所示。

图2 中纤板生产线简图Fig.2 MDF Production Line Sketch

该机器人的D-H 参数、相应约束条件以及各机械臂的相关参数见文献[13]，将机器人在作业过程中所要经过的路径点的直角坐标转换成关节空间中六个关节的角度，得到各个关节的角度，如表1 所示。该生产线包括以下四个工位：取料工位、横切工位、纵切工位和卸料工位。机械手末端吸盘夹具在整个运动过程的轨迹为：A→B→C→D→E→D→F→G→F→H→I→J→A，将这些路径点连接起来构成的空间轨迹，如图3 所示。具体运动过程描述如下：

图3 机器人末端吸盘夹具空间运动轨迹Fig.3 The Space Motion Trajectory of the End Sucker of the Robot

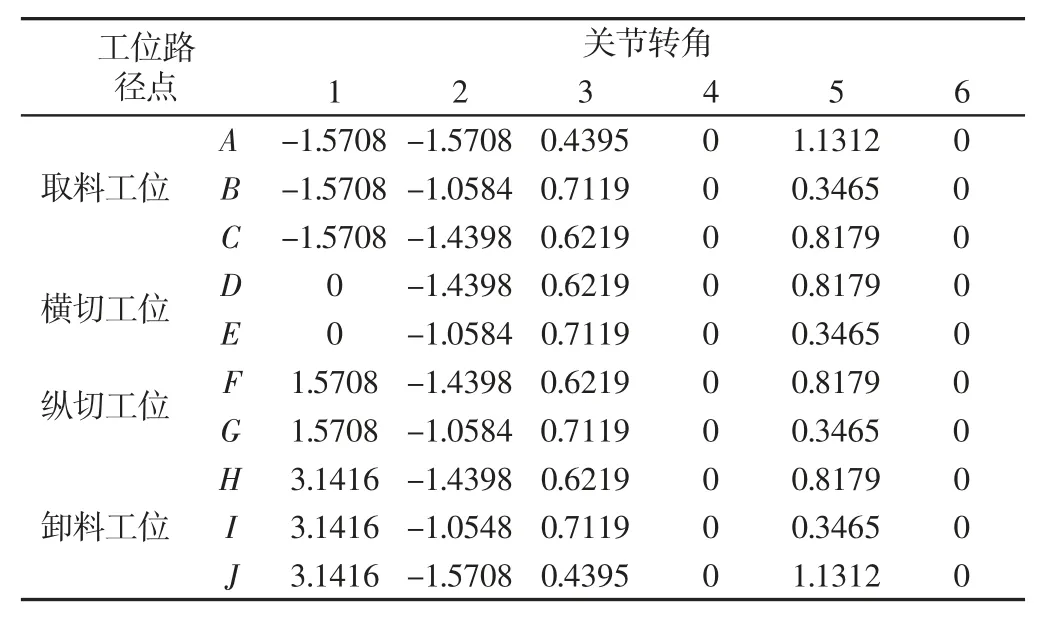
表1 工位路径点对应的关节转角Tab.1 Joint Angle Corresponding to the Station Path Point

第一步：在取料工位取料

当输入装置将待加工的中纤板运送到预定地点时，机械手末端吸盘夹具从初始位置点A下降到传送带上方B处夹取中纤板，提起中纤板到位置C处，然后机器人基座旋转，切换至横切工位D点处。

第二步：对原材料进行横切

机械手从D点下降到横切工作台E点处，待横切完成后，提起中纤板到位置点D，然后基座旋转，机械手切换到纵切工位上方F点处。

第三步：对原材料进行纵切

机械手从F点下降到纵切工作台G点处，待纵切完成后，提起中纤板到位置点F，基座旋转，机械手切换到放料工位上方H点处。

第四步：将加工好的中纤板放到指定位置

机械手从点H处下降到卸料工作台上点I处，待将加工好的中纤板放到输出装置上之后，机械手末端吸盘夹具提起到位置点J处，然后机器人基座旋转，机械手回到起始位置点A处，一个加工周期结束。

对于能耗问题，有负载相对无负载只是多一个对重力做功，对具体问题无多大影响。不考虑负载，只研究机器人自身在这个过程的能耗。按照运行距离长短将机器人在整个生产周期的动作分为四类：①AB，IJ；②BC，DE，ED，FG，GF，HI；③CD，DF，FH；④JA；令每一类动作的初始时间间隔分别为3.5s，3s，3.5s，5s（注：初始时间间隔只是时间的约束，并不影响目标函数的趋势），在MATLAB 中改进粒子群算法的基本参数分别为：群体规模=100，粒子迭代次数=100，拉格朗日乘子和惩罚因子的最大更新次数=100，初始拉格朗日乘子，初始惩罚因子，约束误差精度，收敛精度。在第三类和第四类运动中，只有机器人的基座在运动，其产生的力矩很小可以忽略不计[13]，所以可以认为这两类运动过程的能耗为0，但是由于力矩、速度、加速度和二次加速度的限制，在这两类运动过程中，机器人的作业时间必须大于相应轨迹下的最短作业时间。

当采用三次多项式拟合两点之间的轨迹时，利用改进的粒子群算法求得这四类运动的最小运动时间分别为1.2936s，1.0915s，2.1500s，3.7496s。当采用五次多项式拟合两点之间的轨迹时，得到这四类运动的最小运动时间分别为2.2123s，1.8666s，3.1347s，4.6012s。针对第一类和第二类运动，用改进PSO 算法对不同权值下的目标函数进行优化，得到的结果，如表2 所示。

表2 优化结果Tab.2 Optimization Results

（1）单个周期两种轨迹对应的速度和加速度对比

设每一个运动过程之间的时间间隔为1s，工作台转换时，机器人以最大约束速度运行。则对应于情况下，在一个生产周期中，三次多项式轨迹下机器人各关节优化所得的角速度和加速度变化曲线，如图4 所示，五次多项式轨迹下各关节优化所得的角速度和加速度变化曲线，如图5 所示。

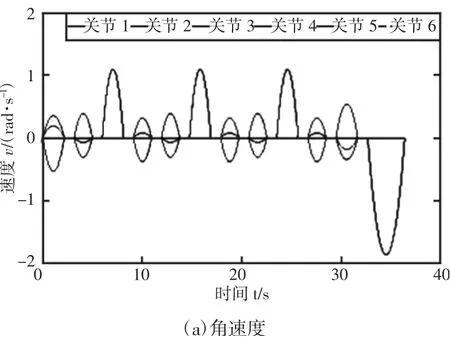
图4 单个周期内三次多项式对应的各关节角速度、加速度变化曲线Fig.4 The Angular Velocity and Acceleration Curve of Each Joint Corresponding to the ThreePolynomial in a Single Cycle

图5 单个周期内五次多项式对应的各关节角速度、加速度变化曲线Fig.5 The Angular Velocity and Acceleration Curve of Each Joint Corresponding to the Quintic Polynomial in a Single Cycle

对比图4 和图5 中单个周期内机器人各关节的角速度和加速度变化可知，虽然两种方法所得结果均满足对应的约束条件，但是在每一段轨迹的起始点和终止点处，三次多项式对应的加速度曲线存在突变，这样不仅会导致机器人的振动和冲击，同时加剧零部件的损伤。

（2）优化结果对比

由表2 可知，在一个生产周期中，三次多项式轨迹优化所得第一类和第二类运动最短总运动时间为9.1362s，对应能耗为44440440.0J，五次多项式优化所得的最短总运动时间为15.6242s，耗能30923689.2J，五次多项式较三次多项式相比时间多71.01%，能耗低30.42%，两种方法的绿色度相同；三次多项式优化所得的第一类和第二类运动的最优能耗为17008154.8J，对应时间为25s，五次多项式优化所得最优能耗为19337492.4J，时间相同，五次多项式较三次多项式相比能耗高13.70%，两种方法绿色度相同；当η1=0.5，η2=0.5 时，三次多项式最优总运动时间为15.2828s，能耗为27480562.8J，五次多项式最优总运动时间为19.7638s，能耗为24453227.6J，此时五次多项式较三次多项式相比时间多29.32%，能耗低11.02%，绿色度相差很小。

综上所述，在绿色度、时间和能耗相近的情况下，考虑机器人的运动精度、机械零部件寿命，选择五次多项式拟合两点之间的轨迹较好。在η1=0.5，η2=0.5 时，单个周期内机器人各关节优化所得的最优运动参数，如图5、图6 所示。

图6 单个周期内五次多项式对应的各关节力矩和二次加速度曲线Fig.6 The Joint Torque and Secondary Acceleration Curve of Each JointCorresponding to the Quintic Polynomial in a Single Cycle