基于稀疏算法的压缩机振动位移信号压缩技术

王 浩，冯 坤，胡明辉，张文海

（北京化工大学 机电工程学院，北京100029）

1 引言

机械设备在线状态监测能够避免危险事故发生、能够有效节约维护成本及提高机械设备运行可靠性、经济性。对于大多数类型的机械设备，例如风力发电机组、石化领域的压缩机组、海上石油平台输油泵等设备，都是各领域内的核心设备；一旦故障停机，会造成巨大的经济损失（例如大型压缩机机组费用达数百万元），甚至发生机毁人亡的严重事故。因此，此类设备需要安装实时在线监测系统，监测系统通过振动传感器和数据采集器采集机械设备主要部位的振动数据，并通过网络将数据实时传输到控制室或其他远程监测部门。然后再实时分析数据，来监测设备的设备状况[1]。

然而，机械设备振动测点多，振动数据量大，大数据量传输难题随之而来。以一个具有50 台压缩机组的石油石化企业为例，每台压缩机安装8 个位移传感器（最少），每个通道以5.12kHz 采样率进行数据采集，数据以64bit 编码（即占用8Byte 空间），整个风场每秒钟产生16.4Mb 的数据，每小时将产生51.2Gb 的数据量，每天累计产生1228.8Gb 的数据量。而这些数据如果要实现实时远程传输，并进行合理的存储，否则将会产生极大的传输带宽和存储空间需求，将会严重降低服务器的使用效率。因此，研发合理的数据压缩技术显得十分重要。数据压缩不仅需要保留振动信号的有用信息，还要保证机械设备的振动信息得到良好的留存。例如，对压缩机来说，设备状况一般要通过频谱分析进行监控，因此有效的数据压缩技术不仅需要大大压缩数据量，而且还要保留信号主要频谱成分[2]。

目前，针对音频数据、图像数据、视频数据等多媒体数据以及心电、脑电等医学领域存在的数据量过大无法有效储存等问题，均提出了不同的数据压缩方法，但用于工程实际的压缩算法少有涉及，并且几乎没有实际工程数据验证。文献[3]通过将小波变换引入到振动数据的压缩中，并分析对比了db小波压缩和余弦压缩的效果。文献[3]中指出,小波系数用来表达数据的奇异性，而傅里叶变换频率成分用来表征数据的非奇异分量。文献[4]研究了离散余弦变换（Discrete Cosine Tranform,DCT）对振动数据压缩的性能，取得了一些有益的效果。

DCT 常用来压缩语音和图像数据，然而DCT 压缩伴随着局部失真，这种失真可能导致错误的故障诊断结论。小波分析（Wavelet Analysis）之所以会得到广泛应用，主要由于其“多分辨率分析”特性，非常适合机械信号的压缩。但文献[3-4]仅仅利用了经典小波分析的最基本特点，难以实现高性能压缩。鉴于对小波分析已经有大量的研究成果，研究重点不在于小波分析，而在于研究小波分析后处理。通过三种常用的最优稀疏表达方法：框架方法（MOF）[5]，基追踪（BP）[6]及匹配追踪（MP）[7]。这三种算法原来主要用于实现信号的稀疏表达，这个特点正好可用于机械振动信号的压缩。

这三种方法的理论和算法均已经得到了良好的研究且趋于成熟，其目的是在小波分析之后产生更加“稀疏”的表达结果；使得同样一组数据用更少的小波分析系数来表达，这就是稀疏表达的含义，这恰恰能够满足振动数据压缩的需求[8-14]。数据压缩语言就是在做概述，这三种方法能够利用小波分解系数，产生最优l个系数对一组长度为N的数据的进行表示（M＜＜N）；而原始数据就被压缩为l个系数，这l个系数重构恢复原始数据。

第1 节，简述了MOF 方法、MP 方法和BP 方法的基本原理，并利用仿真数据简单比较了这三种方法的压缩性能；第2 节利用现场数据对比了三方法的压缩性能。最后，根据对比结果给出结论和建议。

2 稀疏表达方法

近几年来，研究者们一直热衷于数据各种数学表达方法的寻求。除了基于傅里叶变换的方法之外，还产生了很多具有特殊用途的方法，例如：小波分析（wavelet analysis）、小波包变换（wavelet packets）、Gabor 变换、余弦包（cosine packets）等。这些变换和分析方法处理数据的手段类似于用不同的文字但意思相近的手法来表达各种文学作品。在数据变换领域中，可通过定义字典D为P个函数的集合（φD）D∈Γ；并赋予这些函数相应的单位能量值，通常称为原子[15]。一组数据s分解过程可以表示为：

或近似表达为：

式中：αp—变换系数；α—多个系数组成的向量；φp组成字典Φ；—数据压缩后产生的残差。

大多数字典是过完备的（overcomplete），即函数集P的个数大于一组数据的点数。因此，式表示的分解表达在过完备字典下并不是唯一的，类似于同一段文字可以用字典中的不同字词组合表达。正是由于这种不唯一表达的特点，给了我们在多种表达方式上选择最“简短”一种的表达的机会。冗余字典中的数据表达已经提出了多种方法，例如压缩传感理论中提到的匹配追踪（matching pursuit，MP）[8，14]和基追踪（basis pursuit，BP）[5]方法。

2.1 框架方法（MOF）

框架方法通过求解满足最小范数l2的最优解，如式（3）所示。得到稀疏表示原始信号的算子，实现原始信号的稀疏表示[5]。首先框架方法中最优解αT是唯一的。从几何的角度看，框架方法主要目的是从解的空间中选择离原点最近的解。所以可以称作最小解距离、最小二乘解等，可通过线性代数求解该最小二乘解，如式（4）所示。

框架方法存在两个关键的问题：

（1）框架方法没有稀疏选择，字典中任意一个非零元素都会参与分解运算；

（2）框架方法中存在精度限制，原始信号中的冲击特征很难通过算子ΦT（ΦΦT）-1重建，这是由于最小二乘自身的平滑效应导致的。

综上所述可以发现，框架方法的实用性不好，文章后续会通过数据验证该方法的效果。

2.2 匹配追踪（MP）

匹配追踪由Mallat 和Zhang 和提出，该方法逐步迭代选择每个原子，由过完备字典中计算的数据近似表达。首先，该方法将数据向量s投影到一个原子φpn∈D上，计算其残差RS[6]：

由Rs与φp0的正交性可得：

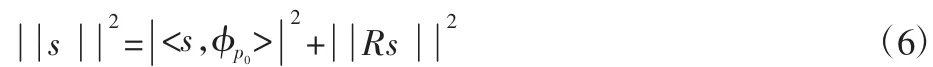
Rms在φpm上的投影为：

Rm+1s和φpm正交得：

对式（9）从m=0 到m=M-1 求和得：

MP 算法通过有限次数迭代后停止时，产生可以替代原始信号的几个原子。当字典正交时，算法效果表现良好。当近似信号只由M＜＜N个原子构成，且算法达到了M 次迭代,近似信号就能够完全恢复潜在的稀疏结构。

2.3 基追踪（BP）

基追踪（BP）一个系数的范数具有最小值l1的近似信号代替原始信号。

基追踪（BP）需要解决凸优化问题[8]，式（12）转化为线性规划，使用全局优化算法进行计算（比如内点法）。

分解系数α 最小化的范数l1可以避免“抵消效应”，所谓抵消效应指的是当匹配追踪（MP）迭代过程中不合适的原子选择，会发生抵消效应，为纠正“抵消效应”算法会变得冗杂[14]。“抵消效应”会增大结果系数的范数l1，导致问题复杂化。基追踪BP 的全局优化算法目的是减小“抵消效应”，为高度相关和冗余字典提供比MP 更精确的稀疏表示。

3 仿真测试

通过构造不平衡振动信号的仿真信号，说明不平衡故障的机理，并利用上述三种稀疏表示方法稀疏表示仿真信号。不平衡故障可以认为是转子在转动过程中，系统不平衡力F引起转子系统的不平稳响应[16]，该不平衡力可以通过式（12）计算得到：

式中：m—转子系统的质量；f—转子的转频；e—转子系统不平衡质量的偏心距；φ—不平衡质量的初始不平衡相位。根据牛顿第二定律，如式（13）所示。可以得到由不平衡力产生的加速度表达式（14）。加速度的二次积分可以得到位移信号x（t），如式（15）所示。可以表示不平衡故障位移信号，为了使仿真信号更加接近实际信号，文章在式（15）所示的信号中加入噪声n（t），如式（16）所示。

苏：传统沙朗舞的服饰也就是羌族传统服饰。男子衣服上有云云花图案，女子衣服上常常绣着牡丹、梅花、桃花、羊角花（杜鹃花）。羌族男子都要包青色或黑色头帕，穿自己织的麻布或蓝布衣服，长过膝盖，腰上系着两米多长的自织带子，外面套一件白色的羊皮褂子。羌族女子一般包黑色、青色或白色头帕，穿蓝布、黑布或麻布衣服，腰间系上绣着各种图案的飘带。以前没有大花花布，只有粗布，现在网上到处都有卖各种颜色的花布。随着年龄的增大，我越来越倾向于鲜艳的花色，喜欢在衣领衣袖上都绣上花边，衣襟和围裙上也绣上图案，色彩醒目漂亮，配上我精细的羌绣手艺，既好看又耐用。

利用MATLAB 软件模拟转子系统不平衡仿真信号，其中转频f=50Hz，偏心距e=0.5，初始不平衡相位φ=30°，信噪比SNR 为5。

时域上的仿真信号，其代表转子系统不平衡故障，如图1 所示。

图1 仿真信号Fig.1 Simulation Signal

仿真过程由超完备小波包字典和用作母小波的Symmlet-8小波（具有8 个消失时刻的对称小波）来完成。有多种小波适合振动信号的压缩，我们选择symb8 小波系数构成冗余字典，比较相同条件下三种稀疏表示方法的效果。通过优化Symmlet 小波可以获得近乎线性的相位及最少的算法支持[15]，所以本研究中选择Symmlet 小波。仿真信号分解结果的频域信息，将上述提到的框架法MOF、匹配追踪MP、基追踪BP 三者作对比，如图2 所示。

我们只保留10%最大幅值以上的成分，并弃掉虚假成分（见第二节）。由图2（a）可以看出基于框架的系数方法MOF 不仅会降低仿真信号故障频率能量，同时滤除了信号的高频成分，信号信息损失严重。图2（b）、图2（c）和图1（b）对比可以发现，基追踪BP（图2（c））不仅增加了仿真信号故障频率的能量，同时增加了高频成分能量，而匹配追踪MP 恰恰相反，同时稍微降低了仿真信号能量。这些方法的压缩性能将在下一节中进一步讨论。

图2 仿真信号频谱Fig.2 Simulation Signal Spectrum

3.1 实验分析

利用现场实际采集的压缩机驱动端水平测试点的振动位移信号来评估上述方法，和仿真过程中使用相同的sym8 小波基。对比压缩比（CR）、均方误差（MSE）、能量保留比例（ER）、频谱相似度四个参数来评价压缩性能，其定义分别如下：

压缩比（CR）：

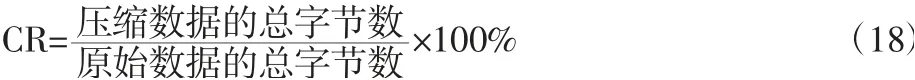
均方误差（MSE）：

式中：si—原始信号；fi—重构后的信号。

频谱相似度：

式中：AS—原始数据的频域能量序列；AF—重构后数据的频域能量序列。

频谱相似度可以评价信号压缩前后振动数据频域信息的相关度，度量压缩信号包含有用信息的多少。这里我们希望频谱相关度值尽可能接近1，即故障信号频域信息尽可能的保留。

通过数据分解技术的研究，对于信号压缩中的编码或量化技术不是研究重点，为了方便，重新定义压缩比如下：

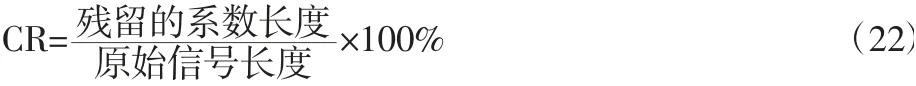
主要的目的是比较第一节提到的三种方法，为简化过程，我们把压缩比固定在10%。并只用均方误差、能量保留比例、频谱相关度作为评价三种方法参数。在数据压缩过程中，一般需要考虑信号在压缩比和均方误差（或能量保留比）之间的差异。但主要比较上述三种方法的压缩效果，可以通过固定压缩比来比较三种方法压缩信号的均方误差和能量保留比例。用频谱相似度作为辅助参数评价三种方法重构信号保留信号信息（即故障信息）的程度。下面通过实测数据对上述三种方法进行比较分析。

3.2 离心式压缩机驱动端振动数据

压缩机组石油石化行业的心脏，离心压缩机组凭借自身压比及流量的灵活变化，迅速发展并不断应用。同时随着压缩机向着高效、大型化发展，其状态监测显得日益重要，其中不平衡、不对中故障是压缩常见故障，这类故障极易导致压缩机密封磨损等。

图3（a）是所用振动数据—某石化压缩机在线监测系统的机组概貌图，电机驱动压缩机旋转。实时采集12 个测点的振动位移信号，实时采集12 个测点的振动信号并保存。该压缩机在2017年7 月6 日至7 月14 日运行过程中，压缩机驱动端振动信号在转速平稳时发生多次跳动，最终导致压缩机连锁停车，分析后发现，振动信号每次跳动前后压缩机转频及其谐频成分大幅增长，轴心轨迹为不规则椭圆，从压缩机正常信号到引起连锁保护停车时间间隔4s，由上述迹象判断此次跳车与质量脱落或质量附加引起转子不平衡相关。图3（b）是停机检修后的照片，最终现场检修结果为：压缩机入口导向套破碎，压缩机第六级叶片被打坏，可以确定为由于转子质量脱落导致的不平衡故障，最终引起压缩机连锁保护停车。

图3 压缩机振动监测及故障检测Fig.3 Vibration Monitoring and Fault Detection of Compressor

某石化离心压缩机组驱动端不平衡故障振动数据，如图4所示。采样频率是5120Hz，信号采样点数为1024，压缩机转速7987r/min，由不平衡故障的振动信号特征可知，振动信号频谱中的工频133Hz 左右的成分会异常显著。

图4 压缩机不平衡故障振动信号时域波形Fig.4 Time Domain Waveform of Vibration Signal of Compressor Unbalance

用三种方法压缩并重构信号的均方误差、能量保留比和频谱相似度，如表1 所示。三种方法时域上重构后的信号，如图5 所示。

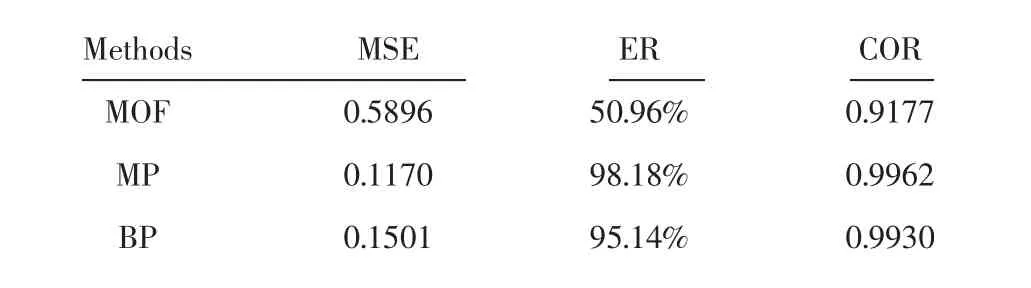
表1 三种方法的性能参数Tab.1 The Performance Parameters of the Three Methods

从表1 及图5 可以得出如下结论：首先，MOF 的均方误差及能量保留比均比MP 和BP 的差，尤其是能量保留比（ER）小于80%，不符合信号压缩的基本要求的；其次，MP 方法的均方误差小于BP 的，而且能量保留比例和频谱相关度都高于BP 的。图5是三种方法重构后信号的时域波形，可以看出，MOF 方法重构后的波形仅保留了低频成分，BP 重构后信号波形的降噪效果较MP好一些；同时，原始信号频谱及其它三种算法重构后信号频谱可以看出，如图6 所示。不平衡故障振动信号特征频率133Hz 附近的成分135.3Hz 异常显著，通过将三种方法和原始信号频谱对比分析后发现，MOF 方法重构后信号频谱中的幅值被降低，而且高频成分消失；MP 方法和BP 方法相比，MP 方法重构得到的信号故障频率幅值和原始信号幅值更为接近。所以可以得出，在信号重构设定压缩比10%时，MP 方法表现更好。图6（d）中，我们观察到BP 降噪能力较好，但是压缩与降噪不同。压缩的目的是利用最少的系数尽可能重现原始信号更多的信息。图6（c）中，MP 方法重构后的振动信号，频谱图中的谱峰与故障特征相关，即为故障特征频率，可以看出转频及其谐频都较好的保留了下来。

图5 重构后不平衡故障信号波形Fig.5 Unbalance Fault Signal Waveform Reconstructed

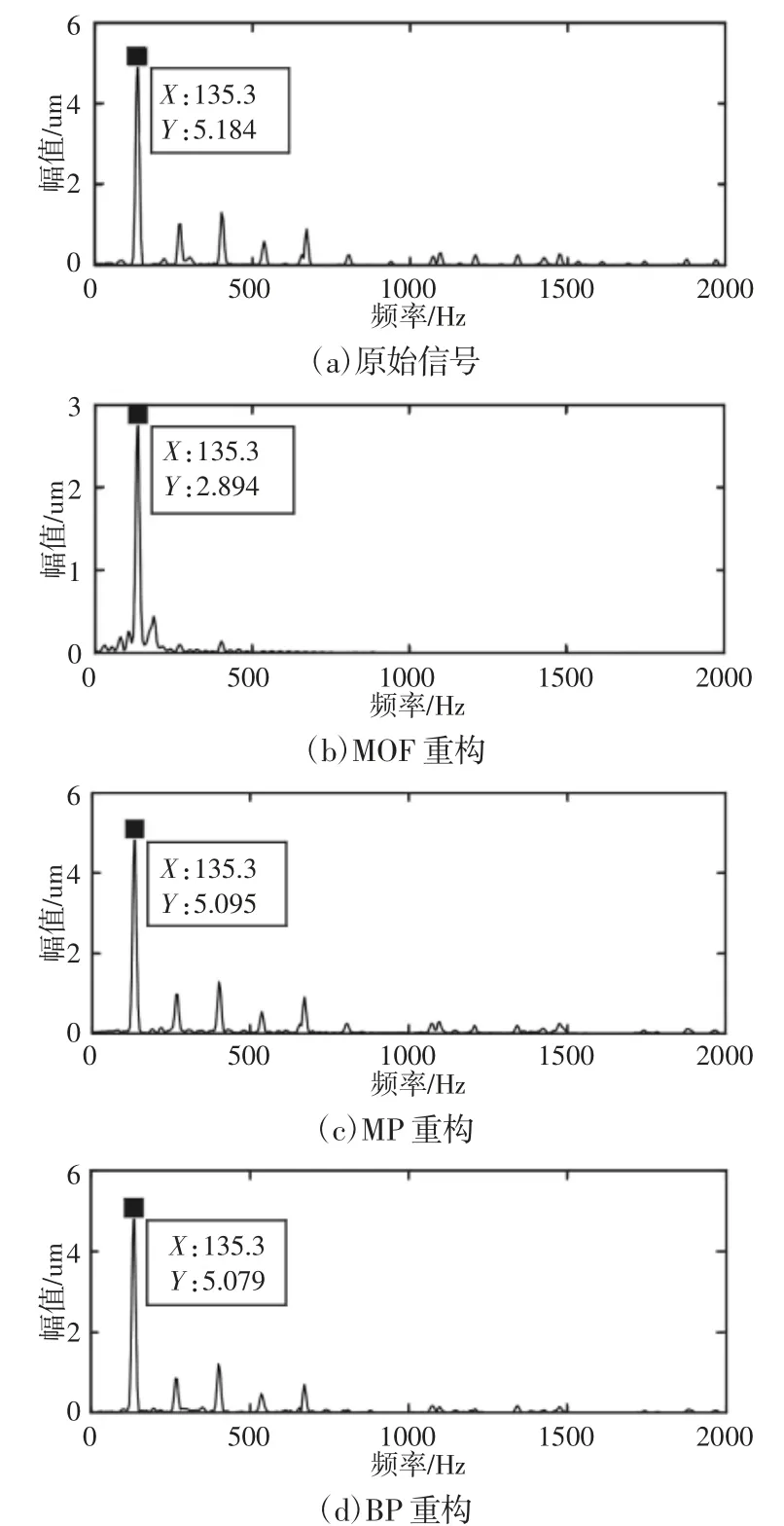
图6 不平衡故障信号频谱Fig.6 Unbalanced Fault Signal Spectrum

4 结论

通过压缩机实测振动数据研究机械振动信号的压缩技术，利用冗余字典中的三种方法：基于框架的方法（MOF）、匹配追踪（MP）及基追踪（BP）压缩信号。小波包字典和sym8 基函数的小波变换分析效果良好。振动数据由现场实际运行的压缩机机组测量得到，数据处理结果表明匹配追踪（MP）方法效果较其它方法好，信号压缩比为10%时，匹配追踪MP 压缩方法可以重建振动信号，完好的保留故障信息。