随机动态规划和粒子群嵌套寻优的PHEV 能量优化

2020-07-22李红娟郭向阳刘宏建

机械设计与制造 2020年7期

李红娟，郭向阳，刘宏建

（1.河南牧业经济学院信息与电子工程学院，河南郑州 450044；2.信息工程大学地理空间信息学院，河南郑州 450002）

1 引言

混合动力汽车使用两种以上能量驱动，具有污染排放低、能源消耗少等优点。对混合动力汽车进行能量管理和优化，可以有效降低能源消耗和污染排放[1]，对缓解能源和环境危机意义重大。

插电式混合动力汽车能量优化策略可以分为两大类：基于规则的控制策略和基于优化的控制策略。基于规则的控制策略是根据车辆和工况确定一定规则，进行不同动力源能量分配，包括确定规则和模糊逻辑两类[2]，当前发展出了传统逻辑与智能算法结合的逻辑规则，即使用粒子群算法、遗传算法等智能算法对逻辑门限值进行优化[3-4]。基于优化的控制策略是通过建立目标函数，将能量优化问题转化为带约束的最优控制问题，分为全局优化和瞬态优化两类。全局优化主要方法有动态规划法、庞特里亚金极小值原理等[5]，此类优化结果只有参考意义，不具备实时控制价值；瞬态优化经典方法为等效燃油消耗最小策略[6]和模型预测控制[7]等。但是插电式混合动力汽车能量管理策略很少考虑电池使用的老化过程，使得优化结果没有算入电池使用成本，或者过度使用电池导致电池寿命缩短，这些都是即将解决的问题。

在考虑电池寿命衰减的前提下优化车辆的能量分配，实现车辆的使用经济性。首先建立了车辆的传动系统模型、电池模型和车速的概率统计模型，将能量控制问题转化为带约束的优化问题，提出了随机动态规划和粒子群嵌套寻优的求解方法，实现了同时降低能量消耗和电池寿命衰减的目标。

2 PHEV 动力系统模型

根据控制系统和仿真需要，本节建立了插电式混合动力汽车动力系统模型。同时控制目标考虑了电池寿命因素，因此建立了电池等效电路模型和寿命模型。

2.1 传动系统模型

带行星齿轮的混合动力汽车动力系统结构，如图1 所示。从图中可以看出，行星齿轮连接着发动机与电机，是整个动力系统的核心部件。行星齿轮中太阳轮、行星架、齿圈间转速与转矩关系为：

式中：Rr—齿圈半径；Rs—太阳轮半径；ωc—行星架角速度；ωs—太阳轮角速度；ωr—齿圈角速度；Tc—行星架转矩；Ts—太阳轮转矩；Tr—齿圈角转矩。行星齿轮中太阳轮与发电机相连，齿圈与电动机相连，行星架与发动机相连，假设齿轮传动的损耗为0，则发动机、电机的转动动力学方程为：

式中：Jg、Je、Jm—发电机、发动机、电动机的转动惯量—发电机、发动机、电动机的角加速度；Tg、Te、Tm—发电机、发动机、电动机转矩；Ttr—牵引力矩；gf—差速齿轮比。电动机转速或齿圈转速与汽车行驶速度关系为：

式中：Rr—轮胎半径；vs—实际车速。

若忽略路面坡度，则汽车行驶过程中的阻力主要包括空气阻力和地面摩擦力，则根据牛顿第二定律，有：

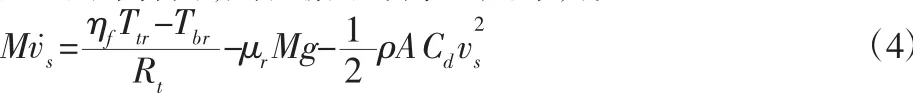
式中：M—整车质量；ηf—差速齿轮传动效率；Ttr—牵引力矩；Tbr—制动力矩；μr—地面摩擦系数；ρ—空气密度；A—受力面积；Cd—空气阻力系数。

发动机燃油消耗率m˙f可以使用制动油耗率构建，即：

式中：fBSFC（ωe，Te）—汽车制动油耗率函数，表示每千瓦时有效功的耗油量，根据文献[8]中的数据，使用三次多项式拟合可以得到函数fBSFC（ωe，Te）的表达式，在此不再给出。

2.2 电池模型

使用等效电路模型中的Rint 模型对电池状态进行描述，得到电池内电流为：

式中：Iba—电池内电流；Uoc—电池内电流；Rba—电池内阻；Pba—电池功率；ηm、ηg—电动机效率和发电机效率；km、kg的取值用于定义电池充放电状态，当km、kg取1 时为充电状态，当km、kg取-1 时为电动状态。

电池荷电状态通过对电流的积分计算得到，即：

式中：S—电池荷电状态；S0—初始时刻电池电量；Qba—电池总电量。

设计的能量优化控制中考虑了电池寿命因素，因此需建立电池寿命模型。当电池可充电量只能达到出厂时可充电量80%时，认为电池寿命结束。研究人员公认，在额定工况下，电池从出厂至寿命结束时流入流出的电量是一个定值，由厂商提供，记为Lf。但是电池大多情况下不工作在标准工况下，过高的电流或温度都会加速电池老化，因此完全依赖累计电量判断电池寿命是不准确的，为了解决这一问题，引入寿命影响因子，建立了有效电量累计模型为：

式中：Aheff—累计有效电量；t0—初始时刻；te—结束时刻；σ（·）—寿命影响因子，且有σ（·）≥1。

将电池寿命的损耗量定义为有效电量累计值Aheff与额定累计值Lf的比值，即：

式中：Lloss—电池寿命损耗量。

由式（8）和式（9）可知，降低电池寿命衰减速率的有效方法是控制寿命影响因子σ（·）工作在较低水平，使累计有效电量Aheff尽量接近额定累计值Lf。电池荷电状态与电池温度是影响电池寿命的最主要因素，因此选取荷电状态和温度作为寿命影响因子的拟合自变量，根据历史数据拟合结果为：

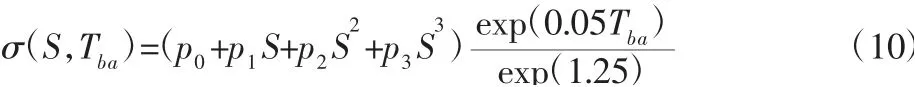
式中：Tba—电池温度，p0=1.73，p1=-1.41，p2=-4.31，p3=8.05。

图2 寿命影响因子Fig.2 Life Influence Factor

为了对寿命影响因子函数有直观的了解，画出寿命影响因子随电池荷电状态和电池温度的变化曲面结果，如图2 所示。分析图2 可知，荷电状态过大或过小时都会使寿命影响因子较大，当荷电状态保持在0.5 左右时寿命影响因子取较小值。电池温度对寿命影响因子的影响是单调的，即寿命影响因子随温度增加而单调增大，温度在30℃以下时寿命影响因子保持较小值。

3 驾驶循环模型与控制问题描述

3.1 驾驶循环模型

控制对象是单位通勤车，即每个工作日在固定时间行驶在固定路线上，由于路线和时段是固定的，行驶过程中的路面坡度、交通信号灯等交通信息是固定的，因此每日的车辆驾驶循环必然具有某种规律。依据通勤车的历史车速信息，建立了车辆的概率统计驾驶循环模型。

以文献[8]中的三周工作日的上下班车速数据为例，出发点至工作地的全程约14km。对15 个工作日的车速数据进行处理，以200m 为单位计算平均车速，得到平均车速信息随路程的分布情况，随机选择3 组数据进行展示，如图3 所示。

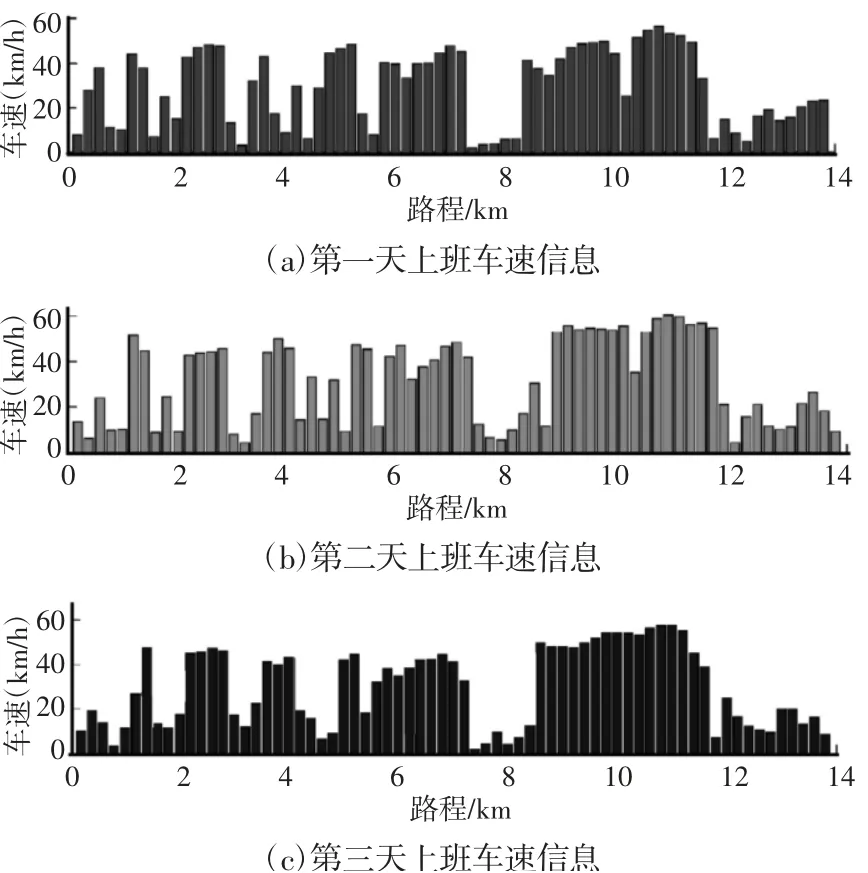
图3 三组上班车速信息Fig.3 3-Group Speed Information on Duty

由图3 可以看出，三天中车辆的平均车速信息具有一定的相似性和明显的规律性。通过对15 个工作日的平均车速信息进行分析，根据相似统计特征将14km 的路程分为8 段，分别为：（0～1.8）km，（1.8～2.8）km，（2.8～4.2）km，（4.2～6）km，（6 ～7.2）km，（7.2～8.8）km，（8.8～11.6）km，（11.6～14）km。假设每段路程上的平均车速信息统计特性均服从正态分布，使用每段路程上的15 个平均车速样本计算车速均值和方差，为：

式中：xj—某段路程第天的平均车速；μˆ—车速均值；σˆ—车速方差。

由此可以得到此路段的车速统计特征，而后以5km/h 为间隔将车速进行等间隔划分，以间隔中心值为代表计算车速区间的概率，最终得到上班途中各路段的车速概率分布图，如图4 所示。

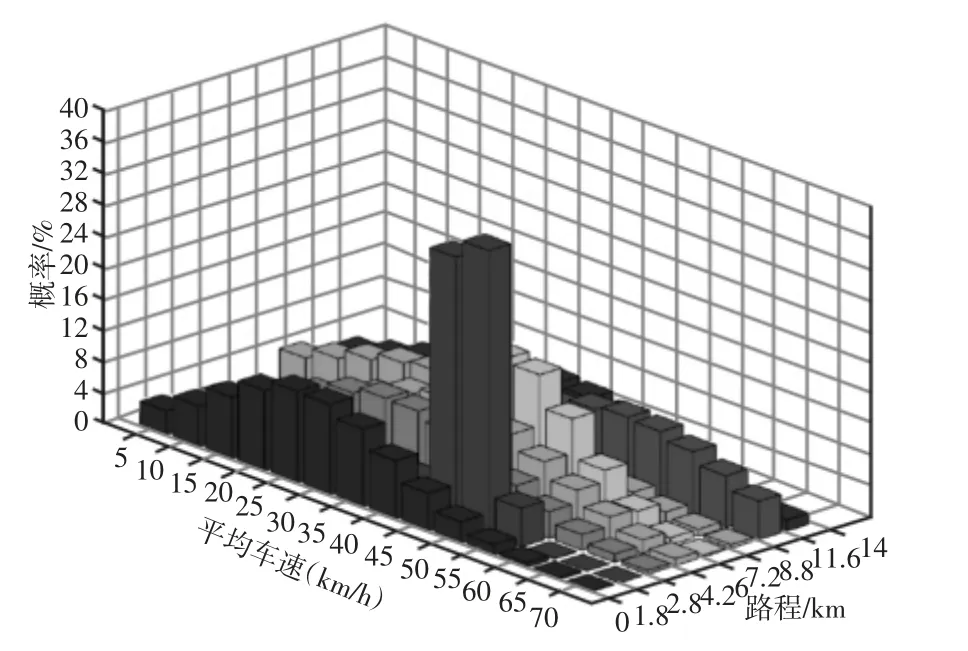
图4 车速概率分布图Fig.4 Speed Probability Distribution

3.2 控制问题描述

插电式混合动力汽车动态模型的一般描述为：

式中：x（t）—状态变量，选择电池荷电状态S（k）为状态变量；u（t）—控制变量，选为发电机转速ωg和电动机转矩Tm；w（t）—随机变量，选为具有统计特征的车速。

根据式（7）得到离散化状态方程为：

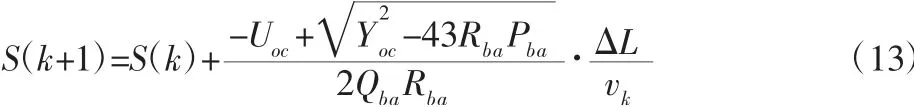
式中：S（k）—k时刻电池荷电状态；vk—k时刻具有统计特性的车速；ΔL—离散化单位距离。

对插电式混合动力汽车的能量优化目标为降低能量消耗和寿命衰减速率，所以成本函数由能量消耗和有效累计电量两部分组成，即：

式中：g（t）—成本函数；θ—寿命衰减系数；（1-θ）—能量消耗系数，用于调整优化中心；Θ—能量消耗目标值；γ—电量累计目标值，两者用于归一化变量；g1（t）、g2（t）—能量消耗函数和有效电量累计函数，计算方法为：

式中：Pel（t）—电池消耗功率；β—电价与油价的换算比。

以上优化问题的约束条件包括荷电状态约束、转速约束和转矩约束，即：

4 随机动态规划和粒子群嵌套寻优

为了对前文给出的控制问题进行求解，提出了随机动态规划与粒子群算法嵌套寻优的求解方法。使用粒子群算法搜索可以平衡能源消耗和寿命衰减的最优系数θ，以此求解随机动态规划的成本函数并给出最优控制律，最优控制律对应的成本函数再反馈给粒子群算法作为适应度函数，实现两种算法的嵌套。

4.1 随机动态规划

随机动态规划的核心内容是策略评价和策略提高，带统计特性的车速状态数量记为s，控制向量维度记为n。

（1）策略评价。对于第k次迭代的控制律uk记为uk=｛uk（1，uk（2），…，uk（n））｝，其评价指标为：

式中：Juk—控制律uk的评价指标；I—s阶单位阵；α∈（0，1）—加速因子；Puk—概率矩阵；guk—成本矩阵，且有：

式中：g（i，uk（i））—使用成本；pij（）—状态转移到状态j的一步转移概率，两者计算方法为：

式中：D—随机变量有限集；Wij（uk（i）—在输入为uk（i）时，使系统由状态i变为j的随机干扰量集合，E为取平均函数。

（2）策略提高。对式（19）进行求解：

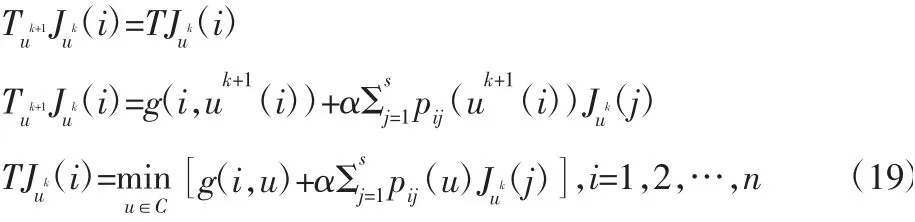
式中：C—控制量有限集。

得到更优的控制策略为：

4.2 嵌套寻优流程及结果

对于可以平衡能源消耗和寿命衰减的最优系数θ，使用粒子群算法进行寻优，由于算法已经成熟，在此不再赘述，只对编码方式和适应度函数进行明确。编码方式为：粒子维度为1 维，使用十进制实数编码方式。适应度函数为式（14）给出的成本函数。基于随机动态规划和粒子群算法嵌套寻优的PHEV 能量优化流程，如图5 所示。使用随机动态规划和粒子群算法嵌套寻优方法对插电式混合动力汽车的8 个路段分别进行能量优化，得到控制策略，如图6 所示。

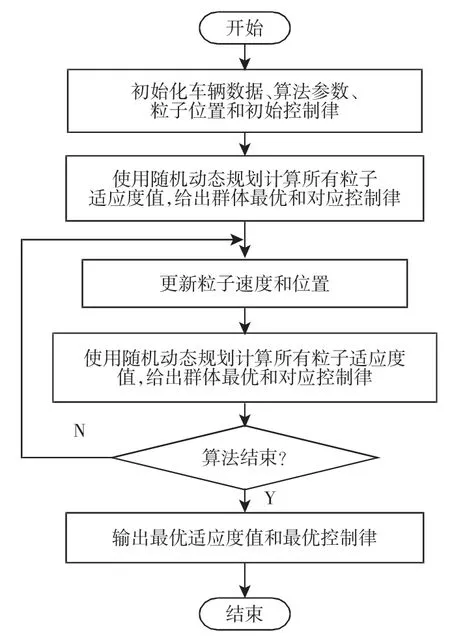
图5 嵌套寻优流程Fig.5 Nesting Optimizing Flowchart

图6 上班全程控制策略Fig.6 Control Strategy of the Whole Journal to the Office

在此对控制策略和控制方法进行明确：在上班途中，前文按照与起始点距离划分为8 段，在每段行程中，按照电池荷电状态查询此时的发电机转速和电动机转矩；根据式（17）给出的状态转移概率，选择最大转移概率对应的车速作为下一时刻的预测车速，再根据式（4）计算车辆需求的牵引力矩，可以得到此时的发动机转矩，从而完成了车辆的能量优化。

5 实验结果及分析

使用GT-SUITE 平台和Simulink 软件共同搭建仿真平台，使用GT-SUITE 平台搭建车辆的电池、发动机、发电机、电动机、行星齿轮等动力系统和传动系统，使用Simulink 软件搭建车辆的控制系统。

5.1 控制效果验证

为了验证随机动态规划与粒子群嵌套寻优方法在插电式混合动力汽车能量管理中的有效性，以文献[8]中第二周周四的驾驶循环为研究对象，以从起始点到工作地、再由工作地回到为一个周期，车辆每次均在起始点充电。控制过程为：上班过程中由第一阶段路程到第八阶段路程依次查询控制量，下班过程中恰好相反，由第八阶段向第一阶段依次查询控制量。使用式（17）给出的状态转移矩阵对车速进行预测，选择转移概率最大的车速为预测车速，实际车速、预测车速及预测误差，如图7（a）所示。控制过程中电池荷电状态及电池温度变化过程，如图7（b）、图7（c）所示。

图7 车速预测与电池状态Fig.7 Forecasting Speed and Battery State

由图7（a）可以看出，使用一步预测矩阵对具有统计特性的车速预测精度较高，实际车速与预测车速的误差极小，为随机动态规划能量分配提供了极高精度的转矩需求。由图7（b）可以看出，一个驾驶周期过程中，SOC 下降较均匀，没有出现因过度追求低成本而提前过度使用电能的现象。由图7（c）可以看出，在整个驾驶周期内，电池温度维持在40℃以下，对比图2 在此温度范围内，电池的寿命影响因子较小，可以减缓电池的寿命衰减速率。以上仿真结果能够说明提出的控制方法具有较高的速度预测精度，且能够减缓电池寿命衰减速率。

5.2 与其他方法对比

为了验证基于嵌套寻优的能量优化方法更加有效，同时使用固定权重系数和粒子群寻优的权重系数对插电式混合动力汽车能量进行管理。固定权重系数θ 的设置方法为：θ 由0 至1 以0.1 为间隔分别取值，当θ=0 时表示仅以消耗能量最少为优化目标，当θ=1 时表示仅以降低寿命衰减速率为优化目标。使用第一周周三的实时交通信息进行仿真，统计固定权重系数和寻优权重系数的控制结果，如图8 所示。

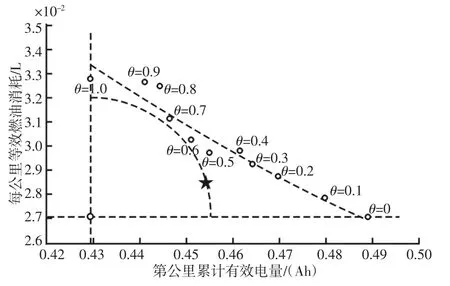
图8 固定权重与优化权重控制结果Fig.8 Control Result of Fixed Weight and Optimized Weight

图8 中一个圆圈为优化权重取固定值时的优化结果，虚线为对θ 取不同值优化结果的拟合曲线；图中绿色五角星为使用粒子群算法寻优得到的最优化结果；以θ=0 和θ=1 的优化结果为标准，确定一个评价基准点，如图中另一个圆圈，此圆圈表示在优化目标不相互矛盾的情况下可以达到的最优结果，以此基准点为评价标准，距离此标准点越近表示结果越优化。从图中可以看出，使用粒子群寻优得到的控制结果好于任何一个固定优化权重的控制结果，这是因为嵌套优化算法中以成本函数为适应度函数搜索最优权重θ，在粒子个体历史最优和种群最优的引导下最优搜索出权重最优值，对应得到最优的车辆控制成本。

为了进一步比较不同控制方法的优劣，使用文献[10]中基于最短路径随机动态规划控制方法和这里的嵌套寻优控制方法同时对文献[8]中第一周周一至周四连续四天的驾驶循环进行控制结果，如表1 所示。从图中可以看出，提出的嵌套寻优控制方法在等价燃油消耗和电池寿命损耗率上均低于文献[10]中的控制方法，嵌套寻优的等价燃油消耗均值比文献[10]方法减少了43.74%，电池寿命损耗率均值减少了35.53%，充分证明了提出的嵌套寻优方法在PHEV 能量优化中的经济性。这是因为嵌套寻优中使用粒子群算法搜索了最优权重系数，在能量消耗和电池寿命衰减之间达到了最优平衡，而文献[10]中基于最短路径随机动态控制方法是一种局部贪婪方法，难以达到全局的最优，所有在PHEV 能量管理上结果的优化程度差别很大。