熔融沉积成型彩色3D 打印控制研究

丁承君，李 瑶

（河北工业大学机械工程学院，天津300401）

1 引言

3D 打印技术[1]，又称快速成型技术，出现在20 世纪80 年代中期，是一种依据数字模型文件，利用液体、粉末、线材等，通过逐层成型的方式来制造三维模型的技术。随着3D 打印机在打印精度和打印速度等方面的的不断完提高，其在医学、工业、生物等领域都得到了广泛应用[2-3]。

多颜色、多材料的3D 打印技术是3D 打印未来的主要发展方向[4]，其在教育、工业制造、艺术创作和建筑等众多领域均有着大量的需求。虽然3D 打印经过几十年的发展，在速度和精度方面得到极大提升，但是大部分工艺只能打印与耗材同样的颜色，导致模型颜色单一，表现力差，这极大地限制了3D 打印的发展，Polyjet 和3DP 是目前比较成熟的全彩3D 打印技术，但是一台设备往往需要十几万甚至几十万，高昂的造价，对其推广起到了很大的限制作用。在诸多工艺中，熔融沉积技术（FDM）成本低，维护简单，制造系统可用于办公环境，打印耗材清洁，更换容易，可打印多种材料。如果研制出可以打印彩色模型的FDM 3D 打印机，对3D 打印的发展无疑是有很大帮助的。对此，文献[5]进行了熔融沉积混色装置的研究，运用TRIZ 理论对3D 打印混色装置进行创新设计，并取得了很好效果。

为了实现FDM 打印彩色模型这一功能，在对原有3D 打印控制策略深入研究的基础上，提出了一种彩色3D 打印控制方案，通过实验验证，该方案可以人为地设置多种颜色，并且可以很好地保证打印精度与稳定性。

2 机械结构组成与运动学分析

该方案主要机械结构采用Hbot 机构，Hbot 机构原理图，如图1 所示。此机构与十字轴、I3、makerbot 机器结构不同的是x、y轴的运动是两个电机共同运动所完成的，电机提供的扭矩更加平稳，因此整个结构的运动比一般结构稳定的多，另外此结构在打印工程中，电机是固定不动的，这显著减轻了运动部分的质量，减小了运动部分的惯性，对打印的速度提升起到很大的作用。

图1 Hbot 机构传动原理示意图Fig．1 Transmission Schematic Diagram of Hbot Mechanism

Hbot 机构两个电机的运动和挤出头的运动关系可以用以下公式表示：

式中：Δs1—M1位移；Δs2—M2位移；Δx—挤出头方向位移；Δy—挤出头方向位移。

由（1）可得：

已知、方向的位移可以由（2）计算出M1、M2的位移，以便于控制系统在已知、位移的情况下，对M1、M2的控制。

3 打印原理与挤出比控制

所提出方案使用三进一出混色挤出头，挤出头结构示意图，如图2 所示。打印原理为控制三种耗材的挤出比，使三种耗材混合出不同的颜色，从而得到彩色的打印效果。三进一出挤出头对应三个挤出电机，令E0、E1、E2分别代表三个挤出电机，∂0、∂1、∂2分别代表三个挤出电机的挤出比，通过在Gcode 中添加M11指令来控制三个挤出电机的挤出比，具体格式为M11f∂0s∂1，例如M11f0.5s0.2即表示∂0=0.5，∂1=0.2，∂2=1-0.5-0.2=0.3。

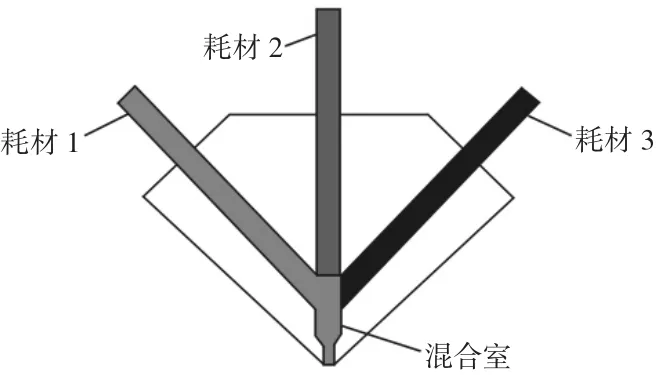
图2 混色挤出头Fig．2 Color-Mixing Extruder

4 系统运动控制

4．1 运动过程转化

此方案中电机均采用步进电机，通过Gcode 设置三个E 轴挤出比分别为∂0、∂1、∂2，且∂0+∂1+∂2=1，此处三挤出比相加为1，是为了确保三个挤出电机的总挤出量和使用单挤出电机时挤出量相等。若挤出头为单进单出挤出头时，E轴步进数为Steps_E，则：

式中：Steps_E0、Steps_E1、Steps_E2-E0、E1、E2-所需步进步数。

令x、y、z方 向 所 需 步 进 步 数 分 别 为Steps_X、Steps_Y、Steps_Z。由Gcode 可以确定Steps_X、Steps_Y、Steps_Z、Steps_E0、Steps_E1、Steps_E2。

令Steps_M1、Steps_M2为电机M1、M2所需步进的步数，由式（2）得：

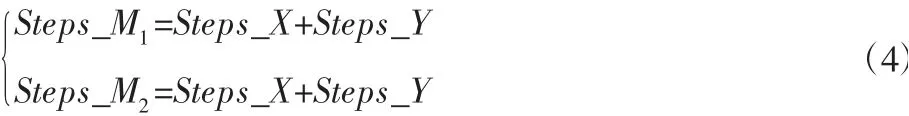
对Steps_M1、Steps_M2、Steps_Z、Steps_E0、Steps_E1、Steps_E26 个步进数共同进行Bresenham 算法插补即可在保证位置和挤出量正确的前提下构建出彩色模型。

4．2 Bresenham 直线算法

在图形算法界，直线生成已经出现了许多有效算法。其中Bresenham 直线算法[6]是最经典的算法之一，其优点在于不需要进行小数和取整运算，只需要整数加法和乘法运算即可。

图3 Bresenham 直线算法示意图Fig．3 Schematic Diagram of Bresenham Linear Algorithm

以第一象限，直线斜率0＜k＜1 为例，如图3 所示。若插补起点为ps（x0，y0），终点为pe（x1，y1），令Δx=x1-x0，Δy=y1-y0，易得Δx＞Δy，插补过程如下：

（1）i=0，Ci=2Δy-Δx。

（2）xi+1=xi+1。

（3）若Ci≥0，yi+1=yi+1，Ci+1=Ci+2（Δy+Δx）；

若Ci＜0，yi+1=yi，Ci+1=Ci+2Δy。

（4）i=i+1，若i=Δx插补结束；否则转至步骤（2）。

式中：Ci—判断如何插补的变量。对于Δx≤Δy的情况，交换公式中x、y的位置即可，可以看出对于坐标变化大的方向每次都前进一个单位。

以XY平面为例，对应电机为M1、M2。令步进电机脉冲当量为step0，其相当于图3 中的栅格边长，这样就可以把打印机工作区域以step0为最小单元进行栅格化，坐标的变化对应电机脉冲的变化，这样Bresenham 算法就可以和步进电机的控制对应起来。若打印轨迹为从Ps到Pe，由以上分析可知，需步进步数最大的电机每次插补都会步进一个step0，定义步进步数最大的电机为基准电机，其所需步进步数为step_max。由式（4）知steps_M1＞steps_M2，则M1为基准电机，插补过程如下：

（2）向基准电机输出一个脉冲。

（4）Steps_C=Steps_C+1，i=i+1，若Steps_C等于Steps_max，插补完成；否则，转至（2）。

Steps_C—基准电机所完成步进数。

若Steps_M1≤Steps_M2，交换Steps_M1、Steps_M2位置即可，因为提出的方案中包含6 个电机，具体实现为先找到基准电机，即六个电机中步进步数最大的电机，计算出Steps_max，再令Steps_max与Steps_M1、Steps_M2、Steps_Z、Steps_E0、Steps_E1、Steps_E2分 别进行Bresenham 直线插补，当Steps_C=Steps_max 时，插补完成。

为简要说明，记上述XY平面插补步骤中步骤（3）为M2针对基准电机的一个Bresenham 插补单元，令CM1，i、CM2，i、CZ，i、CE0，i、CE1，i，CE2，i分别为判断电机M1、M2、Z、E0、E1、E2如何插补的变量，其初始化、更新与上述插补算法相同，则6 个电机插补流程图，如图4 所示。如果基准电机与基准电机执行Bresenham 插补，易得其每次都步进一个单位，所以图4 插补流程与上述原理是等价的。

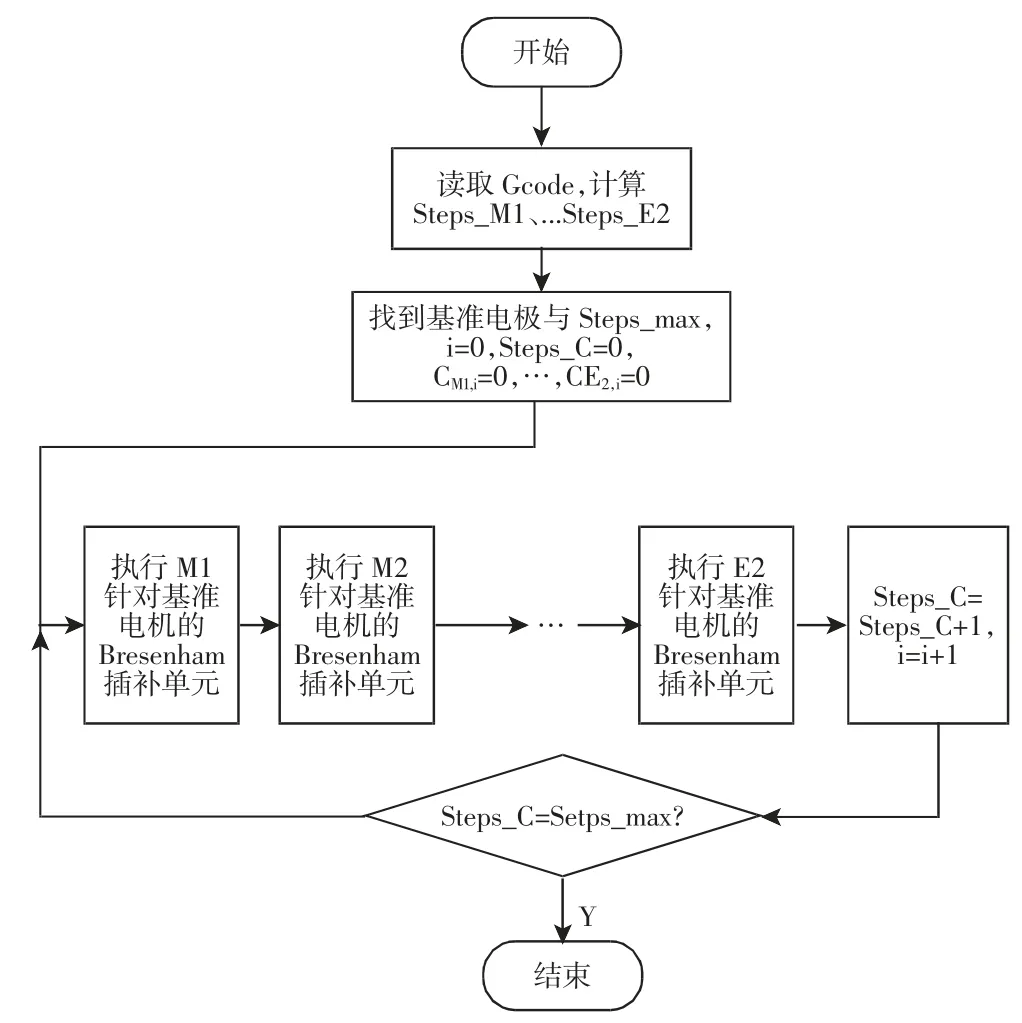
图4 插补流程图Fig．4 Interpolation Flow Chart

4．3 三次多项式型加减速

在3D 打印工作过程中，为了保证执行机构良好的运动精度和较高的打印速度，需要对每个运动轴进行加减速控制，如果加减速控制不好，可能会造成步进电机失步、超步，机械机构产生振动，从而对加工精度造成影响，对机器也会造成很大损伤[7]。

步进电机加减速主要分为梯型加减速，指数型加减速，S 型加减速[8-9]。其中，梯型加减速与指数型加减速会引起加速度的突变，造成柔性冲击，降低成型件的成型质量与机械系统的使用寿命，S 型加减速可以很好地解决加速度突变的问题，但是其计算复杂，较难满足快速成型系统实时性要求。为解决上述问题，相关学者提出三次多项式型加减速模型[10]，其在加速或减速的起始和终止点加速度没有突变，速度变化平稳，可以有效减小机械的振动，且数学模型简单，可以很好地满足快速成型系统的实时性要求。基于以上所述，采用三次多项式型加减速为数学模型与Bresenham 插补相结合对速度进行调控。

三次多项式的速度数学模型如下：

式中：t—时间；a1，a2，a3，a4—待定参数，求式（5）积分得位移s（t），求导得加速度a（t），其数学模型如下：

假设初始速度与终止速度分别为V1，V2，加减速终止时间为tf。现以加速过程进行阐述，即V1＜V2，将加速过程平移，使起始时间t=0，令整体系统最大加速度为Amax，Amax具体值需要根据系统整体性能来确定。令：

式中：A（t）—二次多项式，其极值点在关于对称，得由式（7）求解各参数代处取到，A（t）变化入式（5）、式（6）可得：

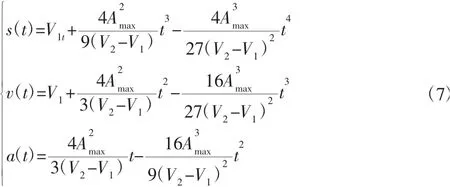
由式（10）可得三次多项式加减速的速度与加速度图像如图5 所示，可以看出在加速的过程中系统加速度无突变，因此系统运动具有较高的柔性。若V1＞V2，易得将Amax换为（-Amax）即可。将每个Gcode 指令规划为一个运动单元，令vi、vf、vo分别为该运动单元的起始速度、Gcode 设定的加工速度和终止速度。若vi与vf，vo与vf两者有一项不相等就需要进行加减速控制。下面以两者均不相等且vi＜vf，vf＞vo这种情况来对调速流程进行说明。将速度调控过程分为一个加速过程、一个匀速过程和一个减速过程。速度与加速度示意图，如图6 所示。其中，0-t1段为加速段，t1-t2段为匀速段，t2-t3段为减速段，显然0-t1段与t2-t3段具体的运动函数模型是不同的，令0-t1段与t2-t3段速度函数表达式分别为va（t）、vd（t），两者均以时间零点为起始点，在实际计算时只需要将t做简单平移即可。由于Bresenham 插补属于脉冲增量插补，因此将Steps_C作为判断速度调控进行到哪一阶段的依据。由于加减速控制实际是利用处理器发出的脉冲频率模拟速度的变化情况，该方案对电机的每一次插补控制都在一个定时中断的中断函数内进行，所以对速度的调控需要控制的实际是定时器的中断时长。根据Bresenham 插补原理，非基准电机的速度存在以下关系：

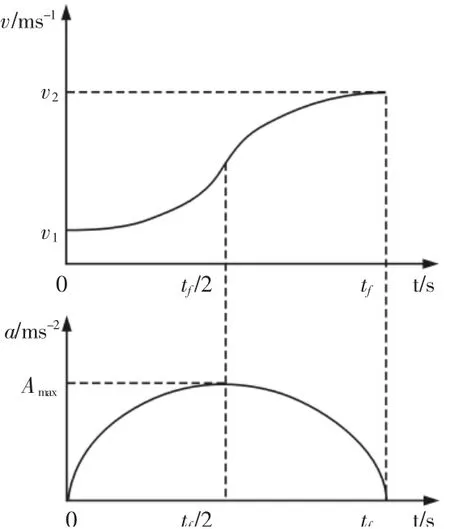
图5 三次多项式型加减速Fig．5 Cubic Polynomial Acc/Dec

图6 运动单元加减速Fig．6 Acc/Dec of Movement Unit

式中：vj—非基准电机速度；

vmax—基准电机速度；

Stepsj—非基准电机该运动单元的步数；

Steps_max—基准电机在该运动单元的步数。

由此可以看出非基准电机的速度变化同样遵循三次多项式模型。因此，通过对具有最大步进步数的基准电机进行三次多项式加减速，其余电机在中断函数中根据Bresenham 直线算法进

行插补即可实现所有电机的三次多项式加减速。

综上，运动单元速度调控具体过程为，第一步，根据式（8）与匀速运动位移和速度的数学关系，计算出基准电机加速、匀速、减速三个阶段走完时所走总步数steps_i、steps_f、steps_o；第二步，完成步数Steps_C与steps_i、steps_f、steps_o比较，判断此时处于该运动单元的哪一阶段或是否进入下一运动单元。第三步，每进行一次中断，速度根据在三个阶段中的哪一阶段进行相应变化，然后根据速度计算出定时器中断时长，设置定时器中断时长。该运动单元速度调控流程图，如图7 所示。其中，ta，td分别为加速与减速所用时间，两者均从零开始计数，Vl为速度调控时的基准电机速度。

图7 速度调控流程图Fig．7 Speed Regulation Flow Chart

5 实验验证

根据提出控制方案搭建样机，如图8 所示。使用自行开发的Gcode 修改软件修改原始Gcode，在其中加入色彩信息，耗材1、耗材2、耗材3 分别采用黄、红、蓝三种颜色PLA 耗材，进行过渡色和多色打印的实验，验证本彩色3D 打印控制方案的可行性。

图8 样机Fig．8 Prototype

5．1 过渡色打印实验

使用Simplify3D 切片软件对模型进行切片处理，设置高度从0．00mm 到175．00mm，∂0保持0．50 不变，∂1从0．50 线性变化到0．00，高度从175．00 到350．00mm，∂0从0．50 线性变化到0．00，∂1从0．00 线性变化到0．50。色彩的过渡效果应该为橙色-绿色-紫色。模型图和打印效果图，如图9 所示。由图9（b）可以看出色彩过渡十分自然。

图9 过渡色打印实验Fig．9 Transition Color Printing Experiment

5．2 多色模型打印

在切片软件中设置双挤出头模式，然后使挤出头1 对应∂0=0.50，∂1=0.50，∂2=0.00，耗材混合颜色为橙色，挤出头2 对应∂0=0.50，∂1=0.00，∂2=0.50，耗材混合颜色为绿色。模型图和打印效果图，如图10 所示。上述实验模型打印精度较高，表面光滑，而且打印时间均超过40h，可以看出，本方案可以较好地实现过渡色和多色打印的任务，并且可以保证很好的稳定性。

图10 多色打印实验Fig．10 Multicolor Printing Experiment

6 结论

彩色FDM 3D 打印是对FDM 工艺的一个极大丰富，在学习现有FDM 3D 打印控制策略的基础上，以Hbot 结构为主要机械结构，将Bresenham 直线算法与三次多项式型加减速算法相结合，实现了彩色3D 打印。通过打印实验验证了该控制方案可以较好地实现彩色3D 打印且具有很高稳定性，因此该控制方案对彩色FDM 3D 打印具有一定的参考价值。