随机森林算法在柴油机故障诊断中的应用

魏东海，王 磊，赵志超，张进杰

（1.北京化工大学机电工程学院诊断与自愈工程研究中心，北京100029；2.中石化重庆天然气管道有限责任公司，重庆404100）

1 引言

柴油发动机在大型汽车、工程机械、船舶、动力发电等领域应用广泛，机器能否稳定健康的运行，直接影响到整套设备的工作状态。因此，对其进行状态监测和故障诊断，能够提高设备运行的可靠性并且减少由于停机带来的生产损失[1]。

近些年来，人工智能技术得到了快速发展，传统的故障诊断方法逐步向智能化故障诊断发展，数据挖掘、模式识别已成为柴油发动机故障诊断领域的一个研究热点[2]。文献[3]实现了BP 神经网络用于高压共轨式电控柴油机故障诊断，但是在训练过程中存在过学习和收敛速度较慢等问题。文献[4]利用支持向量机对船舶柴油机的故障诊断进行了研究，但是支持向量机用于多分类时存在精度不够高等问题。文献[5]基于灰色马尔可夫模型对柴油机磨损趋势进行了预测，虽然准确率在马尔可夫模型优化之后得到了提高，但对历史数据量的要求较大，且在预测模型的推广方面具有一定的局限性。而随机森林算法具有准确度高、泛化性好以及可评估特征重要性等优点，能够更有效的解决多类模式识别问题[6]。运用一种小波包分解和随机森林相结合的方法，对柴油发动机正常、失火、撞缸以及小头瓦磨损四种状态进行故障特征识别研究。实例分析表明，小波包频带能量特征能够很好的从频率角度对信号进行细分，验证了随机森林算法对柴油机故障识别的有效性。

2 随机森林算法原理

2.1 决策树

决策树又称为判定树，是应用于分类的一种树结构。决策树有很多种类型，其中，CART 决策树是一种典型的二叉结构树，已被广泛应用到统计学领域。CART 决策树能够有效地处理数据样本的非线性问题，适用于解决数据样本和目标变量之间关系模糊不明确的复杂性问题。该方法利用基尼指数（Gini）最小化准则进行特征选择，然后自上而下以递归的方法构建模型。Gini 指标用于度量样本的杂质度，对于训练数据集合D，假设共有K个类别，Ck代表第k类的样本子集，为Ck的大小，为D的大小，则集合D的基尼系数为：

假设用特征A对数据进行分割，若特征A为离散特征，则根据A的某一可能取值a将D分为D1和D2：

则已知特征A的条件下集合D的基尼指数为：

Gini 指标的值越小，说明样本的杂质度越低，样本越纯净，建树过程中优先选择Gini 指标小的属性。当属性的种类多于两种的情况下，对各种两类划分的组合分别计算Gini 指标，并且自动选用最小化Gini 指标的划分组合。

当遇到节点中的样本数小于给定阈值、样本集的基尼指数小于给定阈值或没有更多特征这三种情况之一时，决策树算法停止计算。

2.2 随机森林

随机森林实质上属于集成学习的范畴，它最早由文献[7]在1995 年提出。它的工作原理是生成多个单一分类器，各自独立地学习和预测。这些结果最后综合起来预测，因此优于任何一个单分类器或模型所做出的预测。随机森林的基本单元是决策树，将每棵树单独作为一个分类模型进行工作，分类投票结果中的众数作为最终输出。每棵树建立的步骤为：

（1）假定训练集大小为N，采用bootstrap 采样方法，即对于每棵树而言，随机且有放回地从训练集中抽取N个训练样本，作为该树的训练集；

（2）如果每个样本的特征维度为M，从M个特征中随机选取m个特征作为特征子集，其中m应远小于M，每次树进行分裂时，从这m个特征中计算最优分裂方式；

（3）每棵树都会完整生长而没有剪枝过程，因为之前是随机采样，不会出现过拟合。

上述步骤中，随机采样和随机选取特征这两个随机过程对随机森林的分类性能非常重要，它们保证了每棵树之间都是相互独立的，故随机森林不容易陷入过拟合且对噪声具有鲁棒性。而决策树过于依赖训练数据集的准确性，很容易产生过拟合，需要进行剪枝以提高泛化性。

随机森林基于Bagging 思想[8]，如图1 所示。每次从总体N中有放回的进行采样，大约有2/3 的样本被抽出形成一个样本子集，作为一个决策树的训练集。总体样本集中不在样本子集中的剩余样本被称为袋外数据（out-of-bag，OOB），大约有1/3 的样本被排除在森林中的每棵树上。模型预测的准确性利用OOB 误差进行估计，其利用袋外数据评估决策树分类的内部误差。

OOB 误差率作为随机森林泛化误差的一个无偏估计，它的结果近似等于k折交叉验证的结果。因此，随机森林无需进行交叉验证即可保证模型具有较好的泛化性[9]。

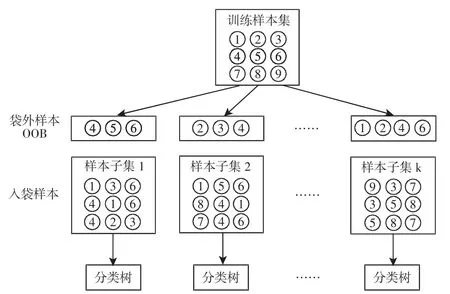
图1 Bagging 过程示意图Fig.1 Bagging Process Schematic

3 实验介绍

3.1 柴油机故障模拟实验台

柴油发动机故障模拟实验在一台型号为WP10.340E32 的六缸柴油机上进行。实验对发动机的瞬时转速、各缸的振动信号、曲轴箱的振动信号以及涡轮增压器的振动信号进行测量，各传感器布置方式为：在发动机飞轮端的齿轮盘上端安装电涡流传感器、在各缸缸盖上安装加速度振动传感器、在曲轴箱对角方向上分别安装速度振动传感器以及在涡轮增压器上安装加速度振动传感器。六缸四冲程直列式柴油发动机的点火顺序为1-5-3-6-2-4，实验台，如图2 所示。

图2 六缸立式柴油发动机实验台Fig.2 Six-Cylinder Vertical Diesel Engine Test Bench

3.2 故障模拟过程

为获取不同故障状态下的柴油机缸盖振动信号，在机组6#缸上模拟了三种常见故障：失火、撞缸和小头瓦磨损故障。具体过程如下：

（1）失火故障：对6#缸高压燃油管进行人为堵塞，其余各缸均保持正常供油，开车运行约10min，转速从580 转逐步上升至约1100 转后又降至580 转附近；

（2）撞缸故障：将加工好的活塞环放入6#缸活塞与缸盖之间，其余各缸均无异物，开车运行约10min，转速稳定在580 转；

（3）小头瓦磨损故障：将6#缸的小头瓦拆下进行人为的磨损损坏，然后重新安装，其余各缸均正常，开车运行约10min，转速稳定在660 转。

4 实例分析

研究时所涉及的算法代码均在MATLAB 环境下实现。系统采样频率为25600Hz，图3 显示了不同故障状态下缸盖振动响应信号，均为单周期信号，其中图3（a）表示正常信号、图3（b）表示失火信号、图3（c）表示小头瓦磨损信号、图3（d）表示撞缸信号。

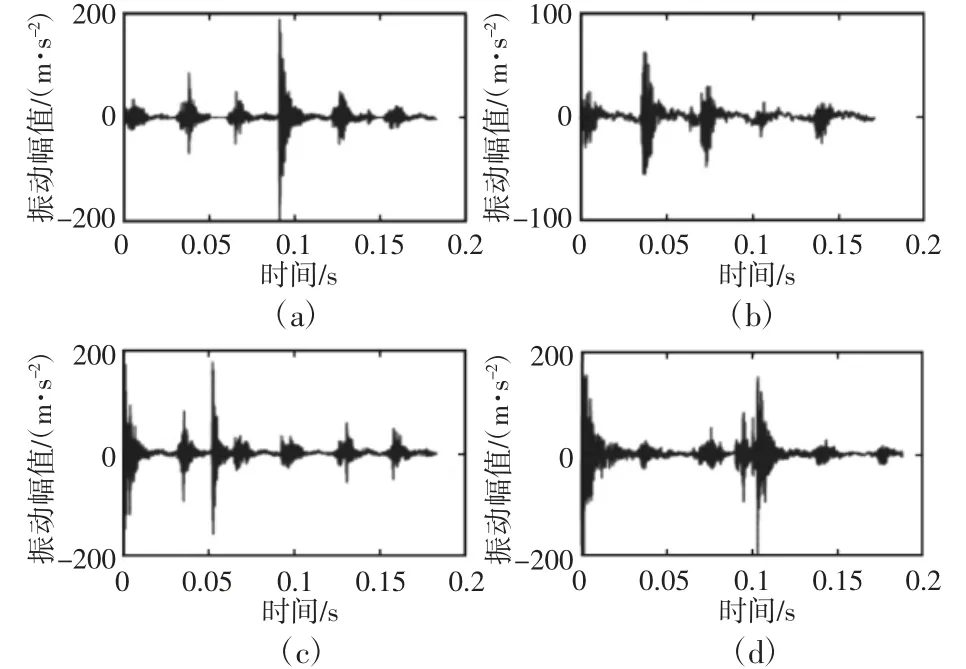
图3 不同故障状态下振动响应信号Fig.3 Vibration Response Signal Under Different Fault Conditions

4.1 小波包分解频带能量特征

小波变换是继傅里叶变换后发展起来的一种信号处理方法，而小波包分析作为小波分析的推广，克服了小波分解在高频段的频率分辨率较差，而在低频段时间分辨率较差的问题。它是一种更精细的信号分析方法，具有分析非线性、非平稳信号的特点，因此非常适合分析柴油发动机缸盖振动信号[10]。

假设进行小波包三层分解，在第三层得到8 个节点信号，分别为S30，S31，S32，S33，S34，S35，S36，S37。每一个节点代表一个频段的信号，其能量为该节点信号所有系数的平方和：

式中：xn—该节点信号中的系数，j=0，1，2，…，7。

能量的绝对数值往往随信号本身情况而不同，但频带能量比可以反映不同频带能量在总能量里面的比例，能更为敏感的从信号中发现柴油机的故障。故对各节点能量进行归一化处理，小波包分解频带能量比定义为：

其中，j=0，1，2，…，7，E=E0+E1+…+E7。

小波包方法将信号分解为8 个频带，但是最高频率成分不在S37，而是在S34，故对第三层小波包分解系数重新排序，各频带从低到高排序依次为：S30，S31，S33，S32，S36，S37，S35，S34。

各频带能量经归一化及重新排序以后，构造以各频带能量比为元素的特征向量：

4.2 故障诊断结果及分析

实验测试获得的数据样本集包括70 组正常、150 组失火、150 组磨损及40 组撞缸数据，总共410 组。每一组数据都是按两个键相截取的单周期信号。训练样本和测试样本的分布情况，如表1 所示。

表1 实验数据样本集Tab.1 Experimental Data Sample Set

对原始数据进行三层小波包分解，将柴油发动机各状态模式下的特征向量T输入到随机森林算法中，训练分类器模型。在随机森林算法构建柴油机故障状态识别模型时，需要确定两个参数：一个是用来构造集成分类器的决策树的数量；另一个是构建特征子集时，随机选取的特征属性的数量。

首先，其他参数固定不变，只改变随机森林中分类树个数，观察训练集中OOB 数据的估计误差。OOB 误差率随分类树的数目的变化情况，如图4 所示。可以看出，初始阶段错误率随着分类树数量的增加迅速降低，在达到75 棵树左右时，OOB 误差率已经趋于平稳。随机森林构建时分类树的数目应该合理选择，过多会大量占用内存空间，导致运算效率降低；太少了会直接影响模型预测的精度，导致识别率下降。综上所述，将随机森林模型中决策树的数量k设定为100。

图4 OOB 与分类树数量的关系Fig.4 Relationship Between OOB and Number of Classification Trees

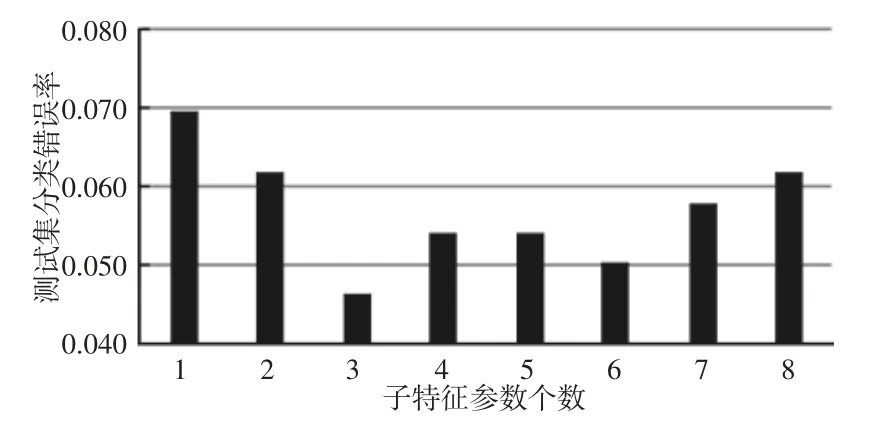
图5 子特征个数与错误率的关系Fig.5 Relationship Between Number of Sub-Feature and Error Rate

其次，第二个需要设定的参数是在分裂过程中随机选取的子特征个数。第一步中已经将随机森林的决策树个数设定为100个，随后改变子特征个数，观察测试集中分类的错误率。选取在测试集分类过程中错误率最低的子特征个数，作为随机森林模型中子特征参数的个数。子特征参数个数随错误率变化的关系，如图5 所示。由图5 可知，子特征参数个数为3 时，在测试集的错误率最低，因此将随机森林模型中随机选取子特征参数个数设定为3个。

另外，小波包分解得到的8 个频带特征的重要性分布如图6所示，从图中可以看出，两个低频段I1、I2和一个高频段I7的能量比特征具有较高的重要性，在随机森林分类树的分裂过程中有着比较大的贡献。

将CART 决策树算法与随机森林算法进行对比，表2 显示了两种分类算法的混合矩阵。可以发现，随机森林错误预测仅为130 个状态中的6 个，综合准确率达到95.4%；而决策树错误预测9 个，综合准确率为93%。证明了集成分类器相比于单一分类器能够更准确的识别柴油机故障。

图6 特征重要性分布Fig.6 Distribution of Feature Importance

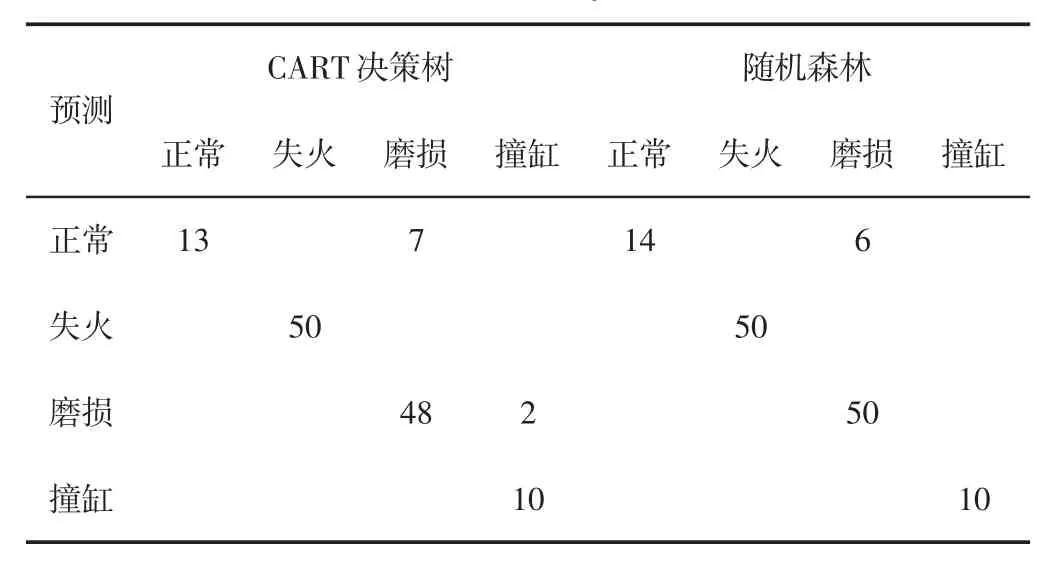
表2 分类器输出的混合矩阵Tab.2 Mixer Matrix Output of Classifier

5 结论

提出了一种小波包分解能量特征提取技术与随机森林分类器相结合的方法，结合实验得出以下结论：

（1）小波包分解可以细化柴油机振动信号，能有效提取非线性、非平稳信号的频域特征。

（2）利用随机森林进行柴油机故障识别，相比于单一分类器，准确率得到了提高，并且无需剪枝，泛化性更好。

（3）随机森林可以对多维特征进行重要性排序，当特征过多导致计算效率下降时，可以通过降维来优化计算。