库区滑坡变形特征分析及发展规律研究

2020-07-22张盛生田成成

中国锰业 2020年3期

张磊，张盛生，田成成

(1. 青海省水文地质及地热地质重点实验室，青海西宁 810008； 2. 青海省水文地质工程地质环境地质调查院，青海西宁 810008)

0 前言

我国滑坡灾害频发，以三峡库区的滑坡灾害尤为发育，涉水滑坡已达两千余个，严重威胁库区航运安全及区内居民的生命财产安全，鉴于滑坡变形是其稳定性的直观体现，因此，开展库区涉水滑坡的变形特征及其发展趋势研究具有重要意义[1-3]。在滑坡变形特征研究方面，已有相应学者开展了相应研究，尚敏等[4]基于盐关滑坡的区域地质条件，开展了滑坡变形特征分析，为其失稳成因研究奠定了基础；汤明高等[5]利用大型离心试验模拟了库岸滑坡的变形特征规律，为其演化过程研究提供了理论基础。上述研究在滑坡变形特征分析方面积累了一定经验，但不同滑坡所处的地质条件具有一定的区域性特征，仍需针对具体滑坡开展针对性研究。在滑坡发展规律研究方面，也有相应学者开展了相应研究，韩贺鸣等[6]利用优化支持向量机模型实现了马家沟滑坡的深部位移预测，所得结果的预测精度较高；岳强等[7]在去噪分析地基础上，利用灰色模型和BP神经网络构建了郑家大沟滑坡的分项预测模型，所得结果较传统预测模型具有相对更高的预测精度；刘人杰等[8]在经验模态分析的基础上，利用优化支持向量机构建了香炉坝村滑坡的变形预测模型，所得预测效果也较为可靠。上述研究利用不同方法实现了滑坡发展规律研究，达到了预期目的，但均未涉及滑坡变形特征与发展规律的联合研究，也未涉及树坪滑坡的相应研究。因此，本文以库区树坪滑坡为工程背景，基于其现场监测成果，先开展其变形特征分析，再利用消除趋势波动分析和优化Elman神经网络构建滑坡发展规律研究模型，以实现其综合研究，以期为树坪滑坡的灾害防治提供一定的参考和借鉴。

1 基本原理

研究包含变形特征分析和发展规律研究两部分，前者是在监测成果基础上的统计分析；后者涉及发展规律研究模型的构建，进而有必要对其各类模型的基本原理进行详述。同时，将该文发展规律分析的思路结构总结如图1所示。

根据图1来看，滑坡发展规律研究可进一步细分为两过程，前一过程是基于滑坡变形数据进行消除趋势波动分析，以判断树坪滑坡的发展趋势；后一过程是利用优化Elman神经网络构建滑坡变形预测模型，即先利用参数优化Elman神经网络模型实现滑坡变形的初步预测，再利用混沌理论实现误差修正预测，两者预测结果叠加即为滑坡变形的最终预测结果。最后，对比发展趋势判断结果与变形预测结果来实现滑坡发展规律的综合研究。

图1 滑坡发展规律研究结构

1.1 发展趋势判断模型的构建

由于消除趋势波动分析(Detrended Fluctuation Analysis，DFA)能有效评价滑坡变形序列的趋势性和长期相关性，进而利用其构建树坪滑坡的发展趋势判断模型[9]。

首先，将趋势性判断指标α的求解过程详述如下。

1)序列重构处理：先求解树坪滑坡变形序列各对应节点处的累计离差Y(i)，再对其进行等距区间划分，即区间长度设置为S，在序列总长度N的条件下，共计可划分为Ns=N/S(取整数)个区间；同时，若Ns不为整数时，按相同长度，对其进行逆序划分，进而得到2Ns个子区间，以充分发挥所有变形节点的作用。

2)局部趋势求解：以各子区间为研究对象，按照最小二乘法原理，对其进行多项式拟合，利用其局部趋势Pv(i)来求解过滤局部趋势的评价参数值Ys(i)。

Ys(i)=Y(i)-Pv(i)

(1)

根据Ys(i)值，即可求得各子序列的方差值Fs。

3)求解波动函数：在求得各子序列方差值的基础上，再对其方差值进行均值求解，以得到标准DFA分析的波动函数。

(2)

4)求解标度指数α：根据上述，可求得子区间长度S条件下的F(S)，并通过改变S大小，即可求得若干散点(F(S)，S)，并通过散点对数处理后进行最小二乘线性拟合，求得直线斜率即为标度指数α。

根据标度指数α的大小即可判断树坪滑坡的趋势性，判据为：

当0<α<0.5时，说明滑坡变形呈反相关趋势，即其发展趋势与当前变形趋势相反，且其值越小，趋势性相对越强。

当α=0.5时，说明滑坡变形不具趋势性，不能判断其发展趋势。

当0.5<α<1时，说明滑坡变形呈正相关趋势，即其发展趋势与当前变形趋势相同，且其值越大，趋势性相对越强。

其次，再利用标度指数α求解相关性参数D：

D=2-α

(3)

以D值大小即可判断滑坡变形序列节点间的相关性，判据为：D值越大，滑坡变形序列节点间的相关性越大；反之，相关性越小。

1.2 变形预测模型的构建

由于Elman神经网络具有4层网络结构，除传统神经网络的输入层、隐层和输出层外，还新增了承接层，有效增加了神经网络模型的动态预测能力和非线性预测能力，因此，利用其构建滑坡变形预测模型具有较强的可行性。由于Elman神经网络已被广泛应用，本文不赘述其基本原理[10-11]。

Elman神经网络虽具有较强的优越性，但也存在一定不足，如收敛速度较慢、易出现局部极值等问题，为保证预测精度，且鉴于粒子群算法(Particle Swarm Optimization，PSO)的全局优化能力，该文利用其优化Elman神经网络的模型参数，但传统PSO算法的惯性权值调整是采用线性递减进行的，缺乏全局与局部的兼顾寻优，为克服该问题，IPSO算法应运而生，其将权值调整采用为动态调整，能有效协调全局与局部的兼顾寻优。因此，该文确定Elman神经网络的参数寻优方法为IPSO算法。

上述IPSO-Elman神经网络模型虽有效保证了模型参数的最优性，但受随机误差等因素的影响，上述优化模型的预测结果仍会存在一定误差，且误差信息具有较强的混沌特征，为保证预测精度，再利用混沌理论构建其误差修正预测模型。

首先，利用Lyapunov指数法判断误差信息的混沌特性，即最大Lyapunov指数大于零时，误差信息具有混沌特性；反之，误差信息不具有混沌特性。其次，当误差信息具有混沌特性时，利用以下步骤进行误差修正预测：①对滑坡变形序列进行相空间重构，并设定合理的嵌入维数和延迟时间参数；②分别利用自相关法和互信息法实现嵌入维数和延迟时间参数的求解；③通过相空间重构预测，反求滑坡变形的误差预测值，进而实现误差修正预测。

2 实例分析

2.1 工程概况

树坪滑坡隶属湖北秭归县，位于三峡大坝上游约47 km处，有公路直达滑坡位置，交通较为便利。据现场勘察成果，滑坡区地貌主要以侵蚀构造地貌和堆积地貌为主；最大、最低高程分别为540，145 m，相对高差约400 m，坡度多间于15(°)～25(°)，整体地形起伏较大，利于滑坡灾害的形成与发生。在地层岩性方面，区内第四系地层主要以残坡积层和滑坡堆积层为主，岩性多是碎块石土，前者多分布于坡度较缓地带，后者分布于滑坡区，厚度间于20～70 m；基岩层主要以三叠系巴东组砂、泥岩为主，多具互层结构，局部出露。滑坡区无显著断裂构造，但节理裂隙较为发育，多以北东向、北向倾斜为主，对滑坡发育具有一定影响。

区内水文条件也较为发育，主要特征如下：①地表水，滑坡区最大地表水系为其前缘长江水系，且斜坡地表冲沟较为发育，雨季降雨易汇集形成地表径流，汇入前缘长江，流量受雨量影响较大；②地下水，区内地下水主要为孔隙水和裂隙水两类，前者多赋存于第四系地层中，赋存量相对较大，后者多赋存于基岩裂隙中，富水性相对较弱。

据现场调查，树坪滑坡整体呈圈椅状，边界特征明显，前缘以长江面为界，左、右两侧分别以龙井沟和叶儿开沟为界，后缘则以拉张裂缝为界，纵向长度约800 m，宽度约700 m，平面面积约55 万m2，平均厚度约50 m，总体积约2 750万m3，属巨型滑坡；同时，滑坡右侧变形较为显著，已发育成明显的强变形区，规模方量也已达1 575万m3。

据钻孔资料，树坪滑坡的物质组成特征分述如下：①滑体土，滑体土主要是崩坡积碎块石土，呈黄褐色、紫红色，局部土石含量差异较大，含量间于20%～80%，岩性多为砂泥岩，上部多为碎块石，磨圆度较差，下部多为粉质粘土，相对较为密实；②滑带土，滑带位于基覆界面，岩性为粉质粘土，厚度间于0.6～1 m，含水量相对较大，夹杂一定量的碎块石，粒径间于2～20 mm，呈次棱角状；③滑床，滑床为三叠系巴东组砂泥岩层，倾向及产状变化差异较大，前者间于135(°)～205(°)之间，后者间于20(°)～35(°)之间；岩性软硬相间，遇水易破坏，节理裂隙较为发育，节理面上分布有石英及方解石等。

2.2 变形特征分析

树坪滑坡属老滑坡，据调查成果，该滑坡于1996年开始出现局部变形，主要表现为前缘走向上的拉张裂缝，造成房屋开裂，并采取搬迁避让处理；自2003年三峡库区蓄水以来，树坪滑坡历年出现规模不一的局部变形破坏，如前缘库岸坍塌、后缘拉张裂缝等。为切实掌握滑坡变形规律，对树坪滑坡进行了地表位移监测，共计布设6个监测点，近似呈“三横两纵”布置，具体布置如图2所示。

图2 树坪滑坡监测点布置

本次分析样本监测时间是2010-2012年，共计3年，对各监测点年变化特征进行统计，结果如图3所示。

由图3可知：随变形时间的持续，年变化量呈增加趋势， ZG85、ZG86和ZG88监测点的增加幅度尤为明显，说明树坪滑坡的历年持续变形是存在的，且变形幅度在逐年增加，趋于不利方向发展。

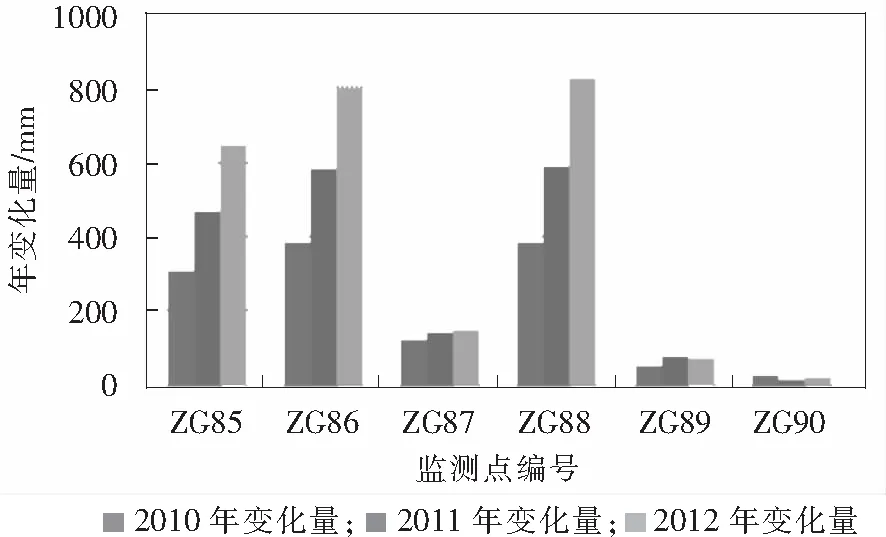
图3 滑坡变形的年变化量对比

结合现场调查成果，得出树坪滑坡右侧强变形区的威胁性相对更大，本文仅以滑坡右侧ZG85、ZG86和ZG87监测点为例，详述其变形速率特征及其发展规律。对3个监测点的特征参数进行统计得表1。

表1 滑坡变形速率特征参数统计 mm/月

在3个监测点中，以ZG85和ZG86监测点的变形速率相对最大，波动范围也相对较广，以ZG86监测点的波动性相对最强，其次是ZG85监测点，而ZG87监测点的波动性相对最弱；同时，在平均变形速率方面，也具有上述类似特征，且平均变形速率值均相对较大，说明树坪滑坡的变形现状较为显著。

由于降雨是滑坡变形的重要诱因，为充分验证降雨对树坪滑坡变形的影响特征，对其月平均降雨量和月平均变形速率进行统计作图得图4。

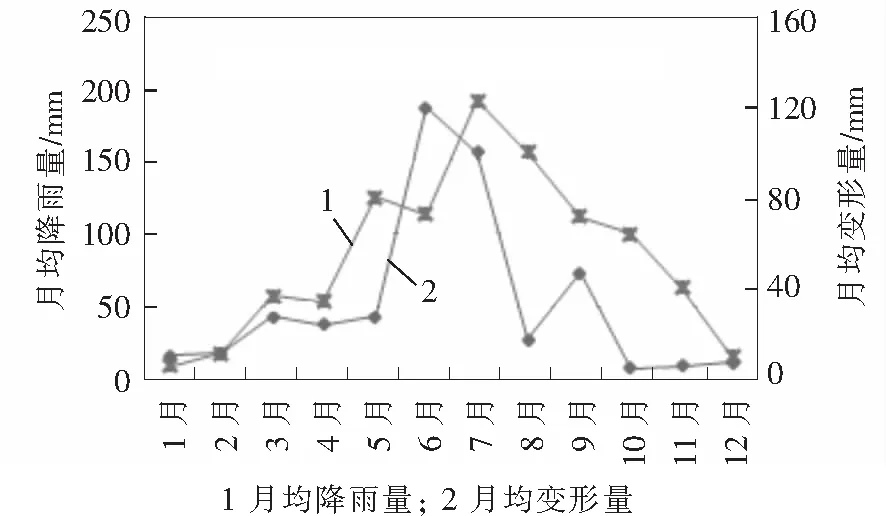
图4 滑坡降雨与变形速率特征对比

由图4可知：月平均降雨量与月平均变形速率具有近似变形特征，即随时间持续，对应特征参数呈先增加后减小趋势，且两者峰值时间相对较近，验证了降雨也是树坪滑坡变形的重要诱因。

对树坪滑坡东侧3个监测点进行3年持续监测，得其变形曲线如图5所示。

图5 树坪滑坡变形曲线

由图5可知：树坪滑坡变形呈持续增加趋势，且以ZG86监测点的累计变形量相对最大，变形值已达1 768.6 mm，其次是ZG85监测点和ZG87监测点，进而说明树坪滑坡变形主要位于中前部，后缘变形相对次之，进而得出前缘长江水位周期性波动对其变形影响较为显著。

根据上述，有效掌握了树坪滑坡的变形特征，总体变形速率较大，且变形量持续增加，滑坡稳定性趋于不利方向发展，验证了开展该滑坡研究的重要性。

2.3 发展规律研究

2.3.1 发展趋势判断分析

先利用DFA分析判断树坪滑坡的发展趋势，结果见表2所示。

表2 滑坡发展趋势评价结果

由表2可知：3个监测点的标度指数α值均大于0.5，说明滑坡变形呈正相关趋势，即其发展趋势与当前变形趋势相同，呈持续增加趋势，其中，以ZG86监测点的α值相对最大，说明其趋势性相对最强，其次是ZG85监测点和ZG87监测点；同时，在相关性方面，ZG87监测点的相关性参数值相对最大，说明其具相对最大的相关性，其次是ZG85监测点和ZG86监测点，且3个监测点的拟合度均较趋近于1，说明其拟合效果较好，所得参数可信度相对较高。

为进一步评价滑坡不同时段的变形趋势，结合田成成等[9]的研究成果，再采用等时段和递增时段方法分析树坪滑坡不同时段的变形趋势特征，其中，等时段指的是各分析阶段等距划分且互不重叠；而递增时段则是等距条件下，分析时段逐步递增。通过计算，得等时段划分评价结果如表3所示。

表3 发展趋势的等时段划分评价结果

由表3可知：不同时段的标度指数存在一定差异，进而说明各监测点在不同时段的变形趋势性也是不一样的，其中，随时间持续，α值具增加趋势，即树坪滑坡后期的变形趋势性相对更强，与图3的分析结果一致；同时，各监测点后期分析结果的相关性均要弱于前期，且各时段的拟合度均趋近于1，具较优的拟合效果。

类比前述，再得递增时段划分评价结果如表4所示。

由表4可知：递增时段划分条件下，不同时段的标度指数值也存在一定差异，且也呈增加趋势，但增加幅度要小于等时段划分的增加幅度，说明等时段划分的评价结果更加趋于保守；同时，各监测点后期分析结果的相关性也要弱于前期，与等时段分析结果一致，且各时段的拟合度也趋近于1，说明求解过程中的拟合效果均较优。

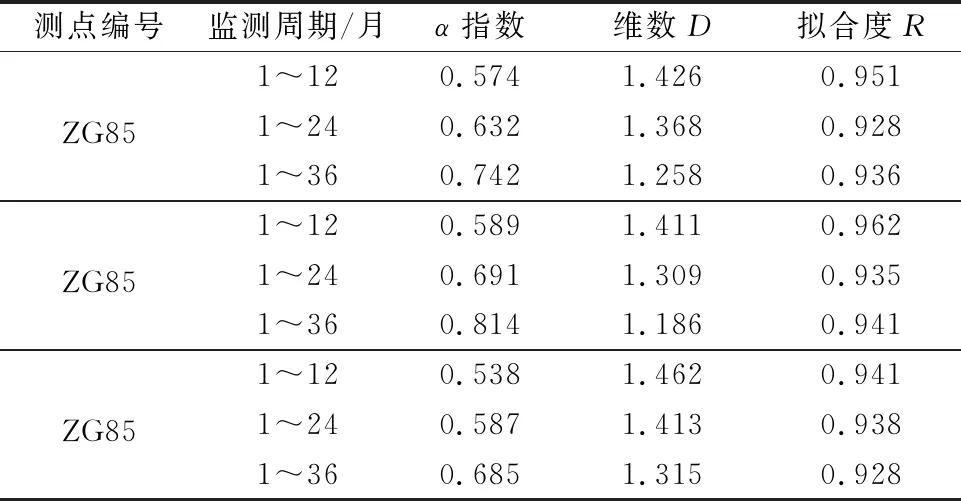
表4 发展趋势的递增时段划分评价结果

通过发展趋势分析，得出树坪滑坡的变形呈持续增加趋势，且增加幅度具阶段性特征，滑坡稳定性趋于减弱。

2.3.2 变形预测研究

为了进一步掌握树坪滑坡的发展规律，再利用混沌理论和Elman神经网络构建滑坡变形预测模型，且为体现该文预测模型的动态预测能力，将监测成果样本划分为两阶段，第1阶段为1～29周期，其1～24周期为训练样本，24～29周期为验证样本；第2阶段为1～37周期，其1～32周期为训练样本，33～37周期为验证样本，并外推预测4个周期，以评价树坪滑坡的发展规律。

同时，为对比分析该文神经网络的有效性，以ZG85监测点第1阶段的预测过程为例，对比分析粒子群算法优化前后及与传统BP神经的预测效果，结果如表5所示。

表5 ZG85监测点第1阶段的初步预测结果

由表5可知：传统BP神经网络和Elman神经网络的预测效果相当，且均劣于参数优化后的预测效果；通过粒子群算法优化，均不同程度的提高的预测精度，并对比两种算法预测结果，得IPSO算法优化后的平均相对误差及其标准差均相对更小，说明IPSO算法较PSO算法具有相对更好的预测精度和稳定性，对Elman神经网络的优化效果相对更佳。

同时，为进一步对比两种优化算法的优化效果，再对两种算法的优化特征参数进行统计，结果如表6所示。

表6 IPSO算法与PSO算法的特征参数统计

由表6可知：IPSO算法相较于PSO算法，具有相对更少的迭代次数和更短的训练时间，且局部优化次数相对更多，充分说明前者具有相对更好的优化能力。

按照预测思路，再利用混沌理论对IPSO-Elman神经网络的预测结果进行误差修正预测，结果见7。

由表7得ZG85监测点第1阶段预测结果的最大、最小相对误差分别为2.13%、1.52%，平均相对误差及其标准值分别为1.87%、0.218%，具有较高的预测精度及稳定性，且预测效果优于IPSO-Elman神经网络的预测结果，初步验证了该文预测模型的有效性。再利用混沌优化IPSO-Elman神经网络对其余两监测点进行第1阶段预测，结果如表8所示。