铝合金毂式节点轴向拉压受力性能有限元分析

曹正罡, 李 亮， 汪天旸, 王志成

(1.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090；2.哈尔滨工业大学 土木工程学院，哈尔滨 150090)

20世纪50年代，国外学者提出可将管件的末端用鸠尾榫与匹配的连接器相接来作为金属连接器，用其建造联锁三角形金属骨架来替代横梁做为建设架构支撑广阔空间[1].随后的几十年里这个最初的设想被不断地完善，形成了目前铝合金网格结构常见节点中的铝合金毂式节点，其凭借成型简单、传力可靠、综合成本低等优势被广泛应用于全球超过35个国家的网格结构工程中，见图1(a).

针对铝合金毂式节点，国外有学者对于节点的抗拉、抗压和抗弯等基本性能做了试验研究[2-4].拉伸试验表明，通过调整构件材性可以保证节点受拉时极限荷载近似等于管材抗拉强度与管面积乘积；压缩试验表明节点受压性能良好，极限荷载转换为管的应力强度时，其安全系数是允许压应力强度的两倍；弯曲试验则证明了沿管端强轴方向节点半刚性的正确性.国内相关研究多集中于对钢制单层网壳嵌入式毂节点基本受力性能研究[5-9].如姜栋等[6]对嵌入式毂式节点做了多组试验，分析了毂体直径、起拱角度等对节点的抗弯刚度和弹性阶段极限弯矩的影响；赵才其等[8-9]提出了两种嵌入式毂节点，并对其进行了拉、压性能试验研究等.然而铝合金毂式节点的材质、拼接方式、嵌入构造形式等相对钢制单层网壳嵌入式毂节点有明显不同，见图1(b)、(c).因此实际上国内外对于空间结构体系中铝合金毂式节点的公开研究较少，对节点几何参数影响效应还缺乏系统的分析和研究.

本文利用软件ABAQUS对25种不同尺寸下的铝合金毂式节点进行了非线性有限元数值分析，研究了毂体槽间距、齿间距、齿宽度、齿深度和齿组数等因素对于节点受拉、受压性能的影响，期望为铝合金毂式节点的设计和应用提供参考.

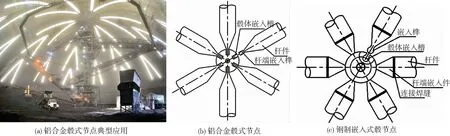
图1 铝合金毂式节点应用及与嵌入式毂节点对比

1 铝合金毂式节点构造

铝合金毂式节点构造见图2(a)，由柱状毂体、杆端嵌入件、盖板、中心螺栓等零件组成.毂体为一圆柱体，是节点的核心构件，它由带沟槽的圆柱形铝合金挤压形成，根据连接杆件的数量和相互位置不同，其上有多道带凹凸纹的锁槽.运用毂式节点连接杆件时，将杆件端头在工厂用特制模具压扁成带有与锁槽相应凹凸纹扁平状的杆端嵌入件，插入毂体上与之相匹配的沟槽内，再在毂体上下端部安置盖板，最后用一根沿毂体轴线方向的螺栓拧紧.节点的细部尺寸及各研究因素见图2(b)，铝合金圆管采用75 mm×10 mm的规格圆管，毂体直径为120 mm，高度为105 mm，螺栓孔直径为20 mm.以算例CD12为标准算例，其余算例编号及主要几何参数见表1，除去与标准算例CD12相同尺寸4个(TL3、TW3、TD1.5、TN4)外，共计25个不同尺寸算例.

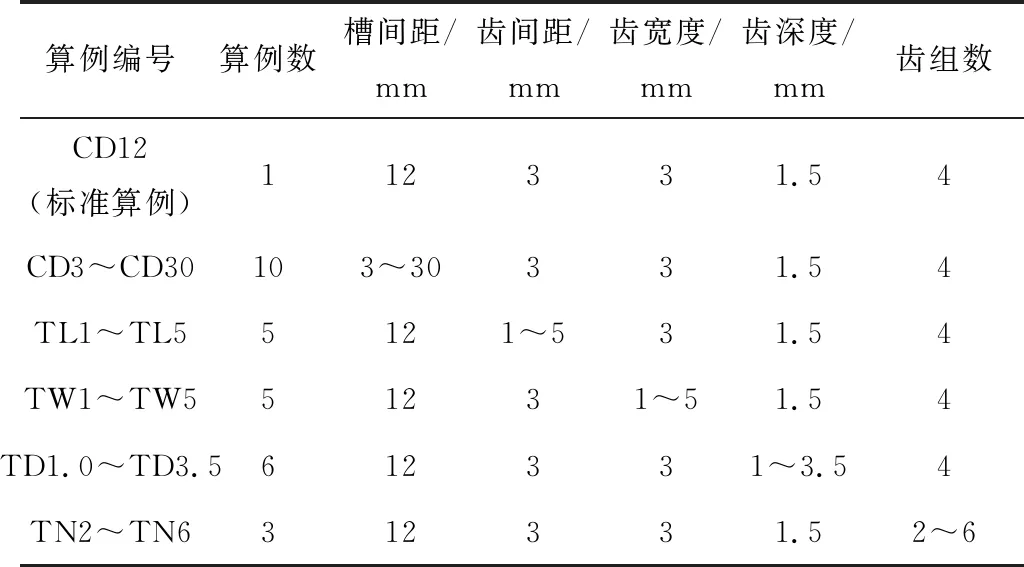
表1 算例主要几何参数

图2 铝合金毂式节点构造详图

2 铝合金毂式节点有限元模拟

2.1 节点有限元模型

参考文献[5]简化建模方式，根据本文所述节点几何上的对称性，运用有限元软件ABAQUS 建立简化后1/2模型，见图3.

对于节点有限元模型采用结构化六面体网格，并选用单元类型为适用于接触分析、克服剪力自锁问题且对应力及中部位节点计算较精确的八节点六面体非协调模式单元C3D81.为获得节点域更精确的应力分布情况，将重点研究的节点内部区域网格尺寸细化，单元布置及网格划分情况见图3.节点内部毂体与嵌入件凹凸齿之间、毂体与螺栓、毂体与盖板之间均采设置接触对，切向采用摩擦接触，摩擦系数取为0.15，法向属性为硬接触[10].

图3 节点有限元模型及网格划分

为模拟节点受轴向荷载作用，如图3所示对简化1/2模型中半毂体的中心面施加固定约束，

考虑

几何非线性，采用荷载加载控制法，避免加载点处的应力集中，对杆件末端加载点处放置一块刚度足够大的加载板，对此加载板施加轴向荷载.对于螺栓预紧力则通过施加螺栓荷载方式来模拟.

节点极限承载力采用极限荷载准则，取荷载-位移曲线中的峰值荷载作为节点极限承载力[11].

2.2 材料本构关系

圆柱形毂体、杆件和盖板均采用6061T6铝合金，采用图4所示Ramberg-Osgood模型，具体参数见表2.螺栓选用10.9级高强螺栓，屈服强度按GB/T 3098.6—2014规范规定为900 MPa，强度准则采用von Mises屈服准则，选用理想弹塑性本构关系模型，见图4(b).

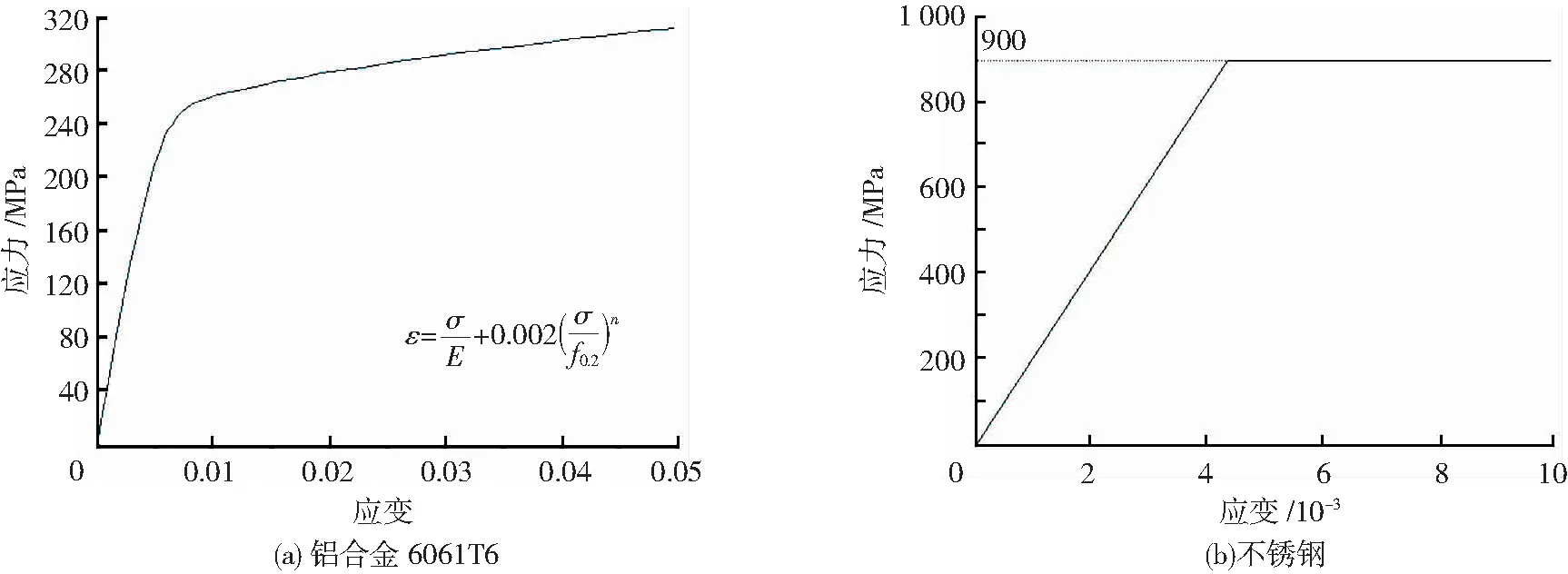
图4 铝合金和不锈钢材料模型

3 有限元参数分析结果

3.1 节点受拉极限状态破坏模式

铝合金毂式节点受拉承载力主要是由毂体与杆件嵌入部分之间凹凸齿槽承担，齿根部受力主要为弯、剪复合受力.不同尺寸下节点受拉一共出现4种破坏模式，见图5，灰色为屈服区域.破坏模式一为大多数尺寸下的破坏情况，毂体凸齿处弯剪破坏；破坏模式二为毂体槽间距较小时的破坏情况，在两槽之间有较大范围屈服区汇聚在一起，毂体最内侧齿槽发生弯剪破坏；破坏模式三为齿间距较小时的破坏情况，毂体最外侧齿槽处有较大范围屈服区汇聚，毂体最外齿槽弯剪破坏；破坏模式四为齿深度较小时的破坏情况，毂体凸齿处剪切破坏.

3.2 毂体槽间距L槽对节点受拉性能影响

本节共计算了10个不同槽间距(算例CD3～CD30)下节点受拉情况，见表3.采用节点受拉时杆件末端的轴向位移和对应荷载，绘制荷载-位移曲线见图6(a)，不同槽间距对应节点抗拉极限荷载见图6(b).

表3 不同毂体槽间距对应节点受拉极限荷载

由表3和图6可知，槽间距从3 mm增至15 mm，节点抗拉极限荷载增加了67.67%；槽间距从18 mm增至30 mm，极限荷载增加了1.31%；结果表明毂体槽间距小于15 mm时，提高槽间距能较大程度增加节点抗拉极限荷载，大于15 mm时，加大槽间距对抗拉极限荷载影响不大.

选择三种不同槽间距下节点受拉极限状态应力云图对比，见图7，当毂体槽间距较小时，在两槽之间呈现较大范围屈服区域汇聚，毂体最内侧凹槽变形明显(破坏模式二)，导致极限荷载较低.随着槽间距离的增大，极限荷载下破坏部位由最内侧凹槽变为毂体凸齿部位(破坏模式一)，承载力随之增大.

图5 节点受拉典型破坏模式

图6 毂体槽间距对节点受拉影响

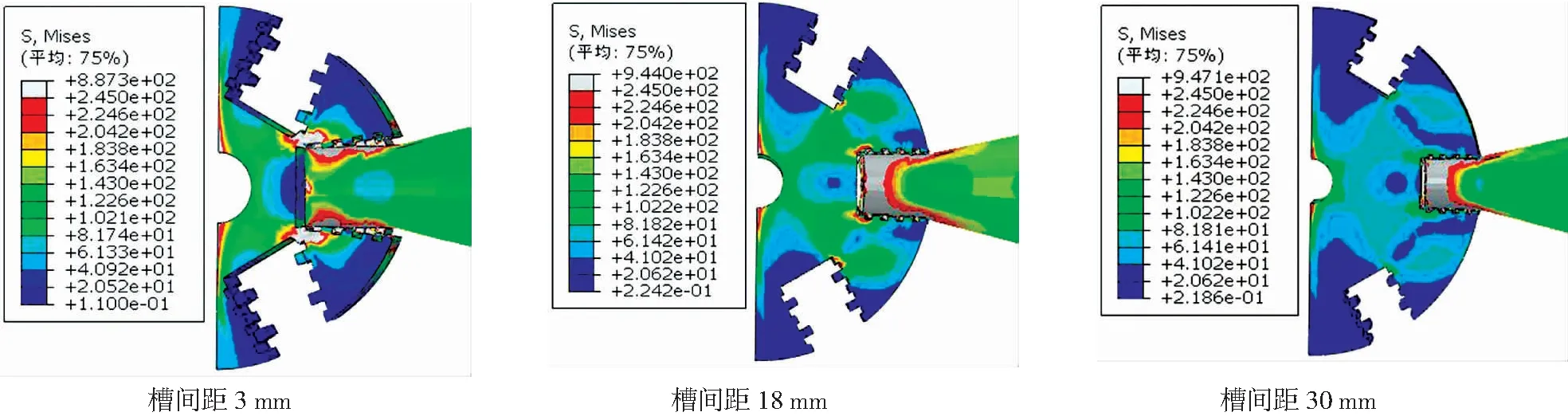
图7 不同槽间距下节点应力云图(MPa)

3.3 齿间距L齿对节点受拉性能影响

本节共计算了5个不同齿间距(算例TL1～TL5)下节点受拉的情况，见表4.采用节点受拉时杆件末端的轴向位移和对应荷载，绘制荷载-位移曲线见图8(a)，不同齿间距对应节点抗拉极限荷载见图8(b).

由表4和图8可知，齿间距从1 mm增至5 mm，节点抗拉极限荷载增加了45.11%，其中每增大1 mm对应荷载分别增大17.83%、14.98%、3.88%、3.10%，可见齿间距从1 mm增至3 mm时，由于破坏位置不同对其抗拉极限承载力增加较多，超过3 mm时，增大齿间距对其影响稍小，但凸齿部屈服面积增大，极限荷载略微增大.

选择3种不同齿间距下节点受拉极限状态应力云图对比，见图9，当齿间距较小时，毂体最外侧齿槽处呈现较大范围屈服区汇聚，毂体最外侧凹槽变形明显(破坏模式三)，导致极限荷载较低.随着齿间距离的增大，杆件嵌入件端部屈服区域增大，极限荷载下破坏部位由最外侧凹槽变为毂体凸齿部位(破坏模式一)，承载力随之增大.

表4 不同齿间距对应节点受拉极限荷载

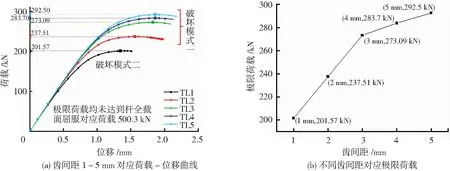
图8 齿间距对节点受拉影响

图9 不同齿间距下节点应力云图(MPa)

3.4 齿宽度d对节点受拉性能影响

本节共计算了5个不同齿宽度(算例TW1～TW5)下节点受拉的情况，见表5.采用节点受拉时杆件末端的轴向位移和对应荷载，绘制荷载-位移曲线见图10(a)，不同齿宽度对应节点抗拉极限荷载见图10(b).

由表5和图10可知，齿宽度从1 mm增至5 mm，节点抗拉极限承载力增加了112.94%，其中每增大1 mm对应荷载分别增大37.97%、23.00%、14.31%、9.76%，结合此前分析可得节点受拉主要靠凹凸齿槽部承载，齿宽度增加使得齿槽部受剪的面积增大，带来抗拉极限荷载明显的增大.齿宽度的变化对节点破坏模式没有明显影响，仍属于破坏模式一，即毂体相应凸齿处弯剪破坏.

表5 不同齿宽度对应节点受拉极限荷载

3.5 齿深度h对节点受拉性能影响

共计算了6个不同齿深度(算例TD1.0～TD3.5)下节点受拉的情况，见表6.采用节点受拉时杆件末端的轴向位移和对应荷载，绘制荷载-位移曲线见图11(a)，不同齿深度对应节点抗拉极限荷载见图11(b).

由表6和图11可知，齿深度从1 mm增至3.5 mm，节点抗拉极限荷载减少了37.66%，每增大0.5 mm对应荷载分别减少0.62%、8.98%、11.83%、9.29%、13.84%.由前述分析可知，节点受拉时齿根部为弯剪破坏，齿深度的增加导致弯矩作用增大，因此节点抗拉极限荷载减少.当齿深度较小时，深度带来的弯矩效应可以忽略，极限状态时，节点表现为毂体凸齿剪切破坏(破坏模式四)，齿深度的增大导致极限状态时节点破坏模式转变为毂体凸齿弯剪破坏(破坏模式一).

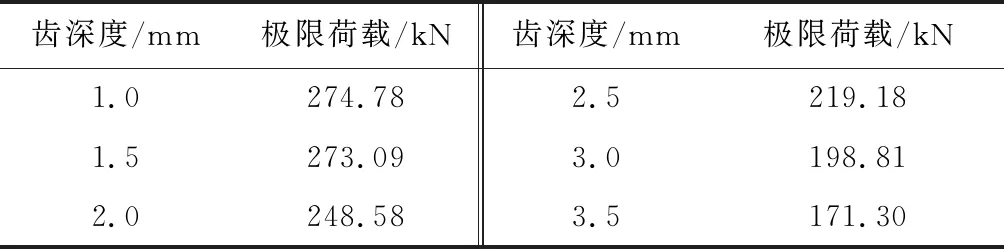
表6 不同齿深度对应节点受拉极限荷载

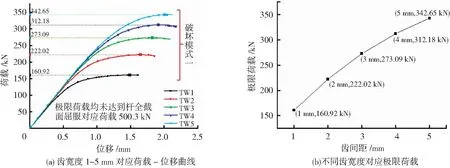
图10 齿宽度对节点受拉影响

图11 齿深度对节点受拉影响

3.6 齿组数n对节点受拉性能影响

本节共计算了3个不同齿组数(算例TN2～TN6)下节点受拉的情况，见表7.采用节点受拉时杆件末端的轴向位移和对应荷载，绘制荷载-位移曲线见图12(a)，不同齿组数对应节点抗拉极限荷载见图12(b).随着齿组数的增加，节点抗拉极限荷载增加122.87%，破坏模式未发生变化，仍属于破坏模式一，即毂体相应凸齿处弯剪破坏.

表7 不同齿组数对应节点受拉极限荷载

3.7 节点抗拉极限承载力公式拟合及设计建议

在上述分析基础上，本文采用多元回归的方法拟合节点抗拉极限承载力的计算公式.经过参数分析可知，槽间距L槽、齿间距L齿、齿宽度d、齿深度h、齿组数n，皆对节点抗拉极限承载力有显著影响.最终拟合时以无量纲参数形式为自变量，设定铝管壁厚t为定值，F0为铝管全截面屈服对应荷载，采用的影响参数有：ξ1=L槽/t、ξ2=L齿/t、ξ3=d/t、ξ4=h/t、n，经过拟合整理后得节点承载力公式为

(1)

对拟合公式进行误差分析，见图13.可见图中各数据点均位于直线y=x周围，且绝大多数点均处于10%误差带范围内.经计算，公式拟合数据和数值模拟结果平均误差为4.44%，拟合公式准确性较高.

图12 齿组数对节点受拉影响

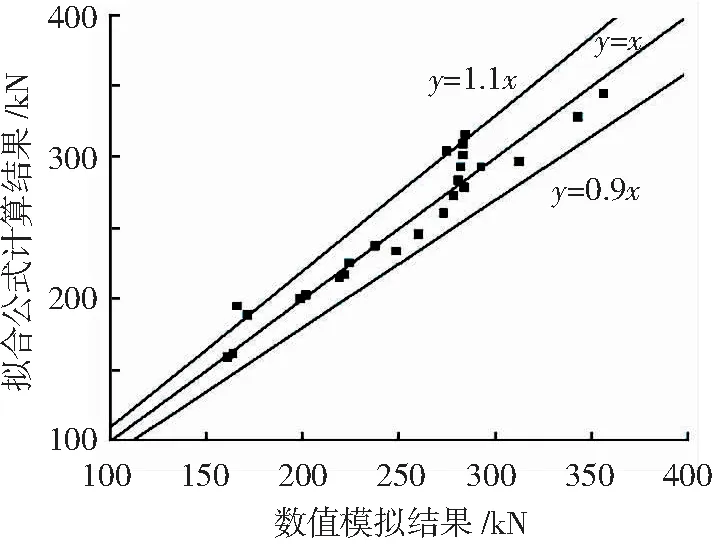
图13 极限承载力公式拟合结果误差分析

在本文所选各参数计算范围内，节点受拉极限状态共出现4种破坏模式，应避免破坏模式二和破坏模式三的发生，这两种情况下毂体中凸齿部分未能充分承载，节点已在其他部位发生破坏，抗拉极限承载力较低.最终根据计算结果给出各影响参数的适宜选择范围：ξ1为1.2～1.8，ξ2为0.3～0.5，ξ3为0.3～0.5，ξ4为0.1～0.2，n为6组.当各参数影响系数小于适宜范围下限值时，节点抗拉极限承载力下降较多，大于上限值时承载力提高不明显，出于节点受力性能和各部件经济性考虑，给出各影响参数的适宜选择范围.

毂体直径应保证相邻嵌入槽中各部件不相碰，通过各影响参数与毂体直径的几何关系，给出毂体直径核算公式为

2(2t+λt+2ξ4t)/sinθ，

(2)

式中：D为毂体直径，mm；θ为毂体中两相邻嵌入槽中轴线之间夹角(两相邻铝管中轴线之间夹角)，rad；λ为嵌入件中两管壁间隔距离与铝管壁厚之间的比值，可取为0.3.

当相邻嵌入槽中轴线之间夹角θ较小时，尚应根据相邻嵌入槽中各部件不相碰的要求核算毂体直径.此时可通过检查可能相碰点至毂体中心的连线与相邻嵌入槽中轴线间的夹角不大于θ的条件进行核算.

3.8 铝合金毂式节点受压

经过有限元分析可知，铝合金毂式节点受压承载力主要由毂体与杆件嵌入部分之间的凹凸齿槽和端面共同承担.极限状态时，杆件挤压过渡部位发生屈曲变形导致失稳破坏，见图14(a)，灰色为屈服区域.本文选用的研究因素的改变对节点受压极限荷载影响较小，见图14(b)，以齿宽度变化为例，节点抗压极限承载力最大值和最小值仅相差0.22%，且其数值接近杆件全截面屈服对应荷载，受压性能明显优于受拉性能.

图14 铝合金毂式节点受压破坏情况及齿宽度对节点承压影响

4 结 论

1)铝合金毂式节点受拉承载力主要由毂体与杆件嵌入部分之间凹凸齿槽承担，齿根部受力主要为弯、剪复合受力；节点域内槽间距、齿间距、齿宽度、齿深度和齿组数的改变对节点抗拉极限荷载有明显影响，极限状态共出现4种破坏模式.

2)铝合金毂式节点受压承载力主要由毂体与杆件嵌入部分之间的凹凸齿槽和端面共同承担；极限状态为失稳破坏；节点受压性能好于受拉性能.

3)在各参数计算范围内，本文给出节点受拉时各因素适宜选择范围：ξ1为1.2～1.8，ξ2为0.3～0.5，ξ3为0.3～0.5，ξ4为0.1～0.2，n为6，并给出了毂体直径设计建议.

4)根据计算结果，本文给出了各参数计算范围内的节点抗拉极限承载力公式.公式的适用性将通过后续试验得到进一步验证.