钢管混凝土中内配钢骨与混凝土黏结性能试验
2020-07-22赵卫平雷永旺王振兴朱彬荣
赵卫平,雷永旺,王振兴,朱彬荣
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083;2.中国电力科学研究院有限公司,北京 100192)
随着建筑结构不断向高性能发展,钢管混凝土结构发展了多种截面类型[1],比如内配工字型钢钢管混凝土和圆中空夹层钢管混凝土.两种构件均是在钢管中先插入钢骨、再浇筑混凝土的组合结构,内配钢骨的加入可有效提高组合结构的延性、抗弯刚度和承载能力[2].由于其优越的受力性能,在大跨越输电线杆塔工程中得到广泛应用[3-4].黏结性能作为内配钢骨(本文指工字型钢和钢管)钢管混凝土优良力学性能的基础,有必要对其黏结性能进行深入研究.
目前关于工字型钢黏结性能的研究主要以型钢混凝土结构为主,并已经取得了一系列研究成果.薛建阳等[5]、邓国专[6]、杨勇[7]对型钢混凝土界面黏结破坏机理进行了细致分析,提出相应的黏结-滑移本构关系;白国良等[8]、陈宗平等[9]等分别研究了型钢再生混凝土、型钢高强混凝土中黏结传力机理,并建立了黏结强度计算式;Roeder等[10]、郑山锁等[11]和应武挡等[12]研究了各因素对黏结强度的影响规律,包括型钢截面尺寸、锚固长度、混凝土保护层厚度、混凝土强度及配箍率等参数;张誉等[13]、郑山锁等[14]和杨勇等[15]通过在拼接工字钢表面沿纵向布贴应变片,获得了黏结应力分布曲线.内配工字型钢钢管混凝土与型钢混凝土在结构上存在明显不同,外钢管与钢筋对内配钢骨的约束机理类似,但两者的约束效果将存在差异;练其安等[16]进行了21个钢管混凝土中内配型钢的拔出试验.结果表明,钢管混凝土中十字型钢与混凝土黏结性能优于角钢与混凝土黏结性能.当前对钢管混凝土中内配钢管与混凝土黏结性能研究报道较少;钱稼茹等[17]研究了钢管混凝土叠合柱中内配钢管与管外混凝土黏结性能,提出了内配钢管与管外混凝土界面抗剪黏结设计建议;王维肖等[18]通过28个钢管混凝土中内配钢管的拉拔试验和推出试验,结果表明内配钢管推出时的黏结强度普遍高于拉拔试验,内配钢管径厚比对黏结强度影响显著.之前研究主要采用对比试验分析各因素对内配钢骨黏结强度的影响,实际上黏结强度的影响因素众多,而无法确定各因素影响黏结强度的主次关系.
本文进行了18个内配钢骨钢管混凝土试件的推出试验,以探讨内配钢骨与混凝土之间的黏结机理;运用正交试验分析,得到各因素影响黏结强度的变化规律及主次关系,并分析黏结应力分布规律;基于实测数据回归分析,提出两种钢骨黏结强度计算方法,可供工程技术人员参考.
1 试验方案
1.1 试件设计
为研究两种钢骨与混凝土黏结性能,共设置两个正交试验组,均考虑3因素3水平.1号试验组为内配工字型钢钢管混凝土试件,研究参数为黏结长度(Le)、混凝土强度(fcu)和工字型钢截面尺寸(SI).2号试验组为圆中空夹层钢管混凝土试件,研究参数为黏结长度(Le)、膨胀剂掺量(v)和内配钢管截面尺寸(SII).选用两个L9(34)正交试验表,共设计18个试件,其截面形式见图1,试件参数见表1.

图1 内配钢骨钢管混凝土横截面
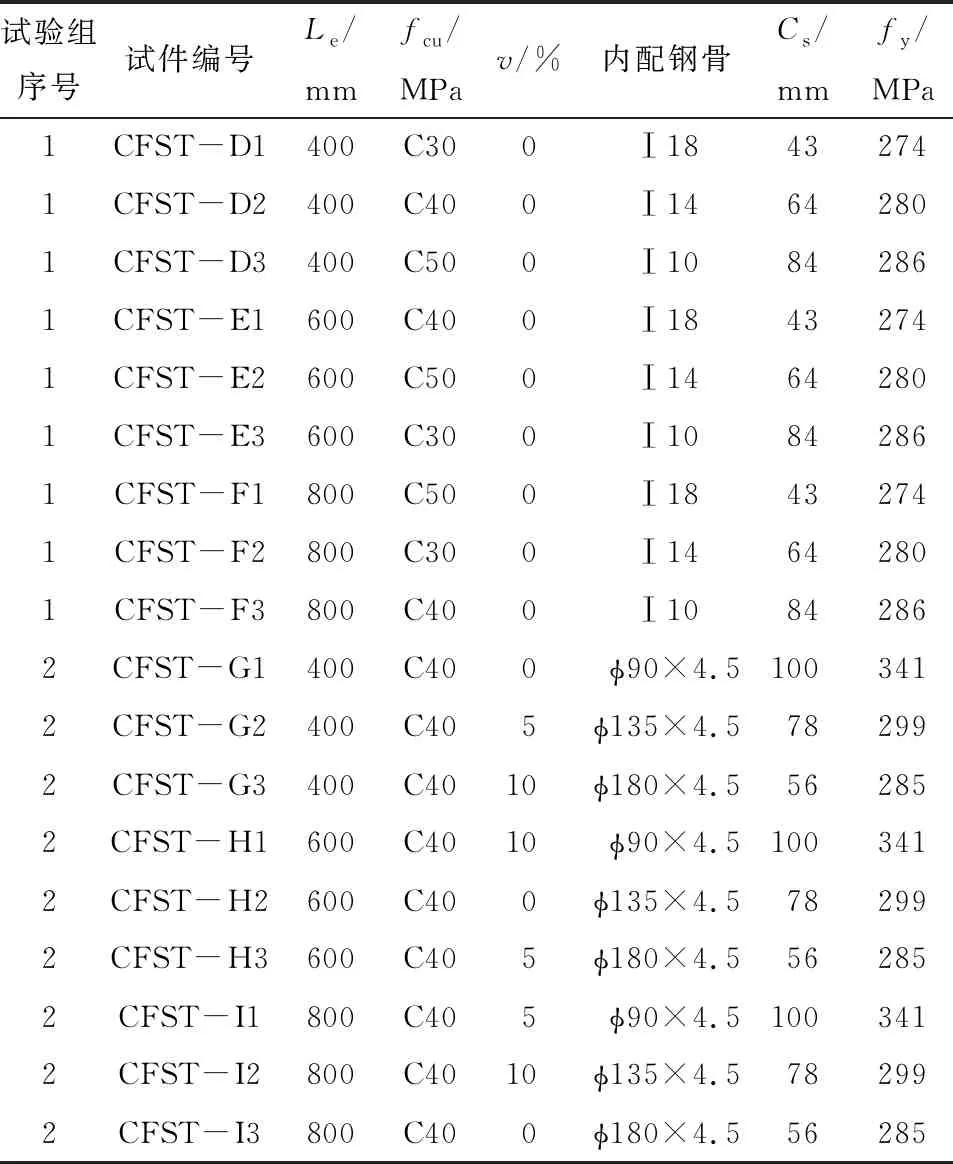
表1 试件设计参数
1.2 材料参数
试验中钢管均采用大跨越输电线塔工程中常用的直缝焊接钢管,经过钢板卷曲成型、埋弧焊工艺生产而成.根据电力行业规范T/CEC 136—2017《输电线路钢管塔用直缝焊管》[19],钢管外径制作允许偏差为±0.5%D,厚度制作允许偏差为-0.3~+1.0 mm.所有外钢管统一采用φ299×4.5,内配钢管采用φ90×4.5、φ135×4.5和φ180×4.5.内配工字型钢采用I10、I14和I18.通过标准拉伸试验,得到外钢管、内配钢骨的材料力学性能指标.混凝土配料采用42.5R硅酸盐水泥、标准中砂和粒径范围为10~20 mm的玄武岩粗骨料,减水剂为标准型聚羧酸减水剂,膨胀剂为硫铝酸钙-氧化钙类混凝土膨胀剂,配合比设计见表2.
1.3 试件制作
为使内配钢骨在推出过程中受力均匀和避免发生局部失稳,在工字型钢加载端加工了方形钢板,在内配钢管加载端加工了环形钢板和加劲肋.在外钢管的垂直对角两侧分别加工一对弯钩和一对角钢,分别用于试件的吊装和位移计的布置.混凝土浇筑时每组预留6个150 mm×150 mm×150 mm混凝土立方体试块,按照标准方法制作并自然养护,其28 d实测强度结果见表2.

表2 混凝土配合比设计
1.4 测试与加载方案
为测试推出试验中内配钢骨表面的应变变化,在工字型钢翼缘外侧、腹板及内配钢管外壁两侧沿纵向先铣槽、再在凹槽内沿纵向布贴应变片,布贴间距为50 mm,最后浇灌环氧树脂,以保护应变片和弥补铣槽带来的几何缺陷,见图2.
推出试验在1 000 kN液压伺服加载试验机上进行,在钢骨加载端上方放置一块略大于钢骨直径的钢垫块,轴向荷载通过钢垫块直接施加于钢骨上,通过黏结力传递给周围的混凝土,加载装置见图3.
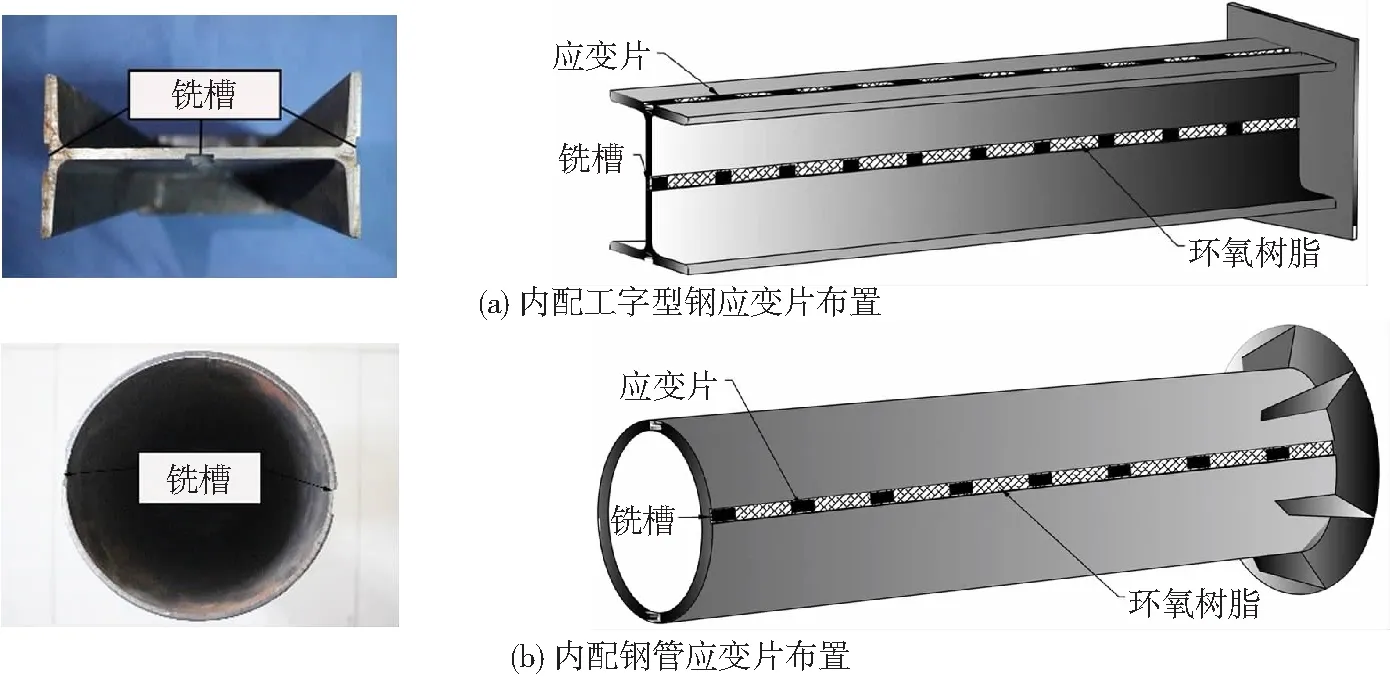
图2 测点布置
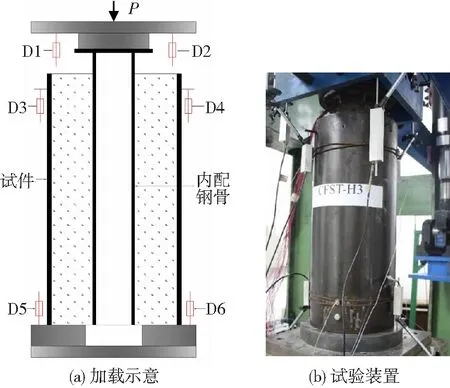
图3 加载装置
正式加载前期采用力值控制,当荷载-滑移曲线开始下降时换用位移控制.为测试内配钢骨与混凝土之间的相对滑移,总共布置6个位移计.位移计D1和D2用于测量内配钢骨加载端的竖向位移;位移计D3和D4用于测量外层钢管的竖向变形;位移计D5和D6用于测量底部支座的竖向位移.
2 试验结果与分析
2.1 试验现象
试验加载初期,内配工字型钢和钢管的竖向位移接近于零,黏结界面无相对滑移;当荷载增大到极限滑移荷载的50%左右时,界面出现相对滑移,位移计D1和D2示数略有增大;当荷载接近峰值时,大部分试件会出现一声巨响,此后钢骨整体向下滑移的速度增大;最后,内配工字型钢和钢管被顺利推出.随内配工字型钢的推出,工字型钢自由端附近的混凝土受到界面抗剪黏结力的作用,出现局部损伤.试验结束后,发现所有试件中内配工字型钢和钢管均未发生屈曲破坏,其界面均为黏结破坏,见图4.

图4 推出试验后破坏形态
2.2 黏结应力-滑移曲线
通过加载系统内置传感器和外置采集设备获得了所有试件的荷载-滑移曲线.为了便于分析,假设黏结应力沿内配钢骨与混凝土接触面均匀分布,采用平均黏结应力计算方法分析界面黏结-滑移机理.黏结应力τ计算公式为
(1)
式中:τ为黏结应力,P为轴向推出荷载,C为内配工字型钢或钢管的横截面外周长,Le为黏结长度.根据式(1)计算得到所有试件在滑移过程中内配钢骨的黏结应力和黏结强度特征值,推出试验结果见表3.
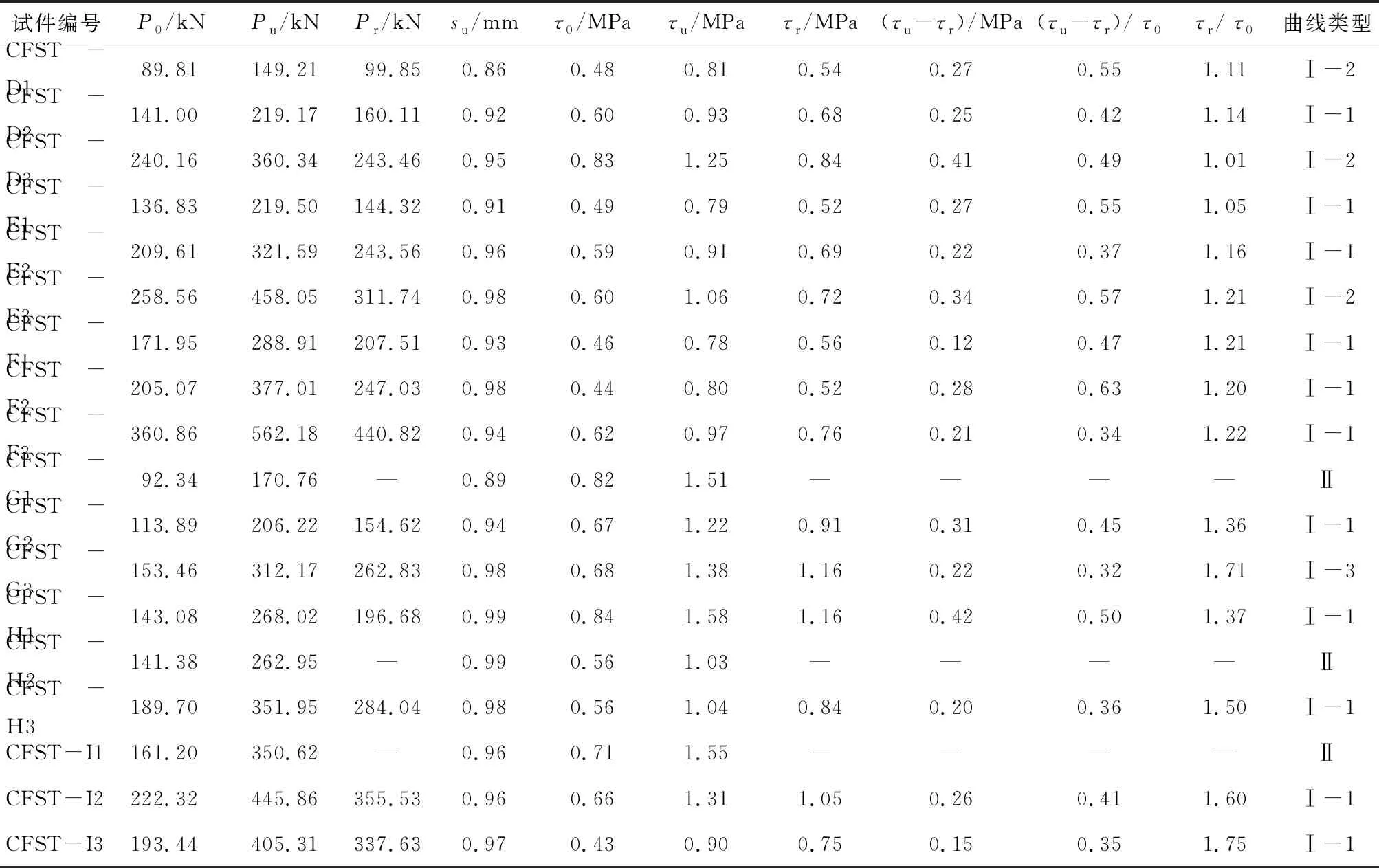
表3 推出试验结果
图5(a)~(e)为18个内配钢骨钢管混凝土试件的黏结应力-滑移(τ-s)曲线,所有曲线在峰值点前呈相似的上升趋势,在峰值点后曲线出现多种发展趋势.根据曲线在峰值点后出现的四种形状特征,图5(f)归纳出了四类典型黏结应力-滑移曲线,将其分为Ⅰ-1、Ⅰ-2、Ⅰ-3和Ⅱ类.结合内配钢骨的滑移过程,所有曲线均包括3个阶段,分别为胶结段、非线性初滑移段和滑移段.
胶结段(OA段):曲线呈直线上升.界面黏结良好,黏结力由化学胶结力构成.A点处黏结应力代表初始黏结强度τ0.内配工字型钢和内配钢管平均初始黏结强度约分别为平均极限黏结强度的60%、50%.
非线性初滑移段(AB段):曲线呈非线性上升.界面开始产生相对滑移,界面剥离从加载端逐渐发展至全界面,化学胶结力彻底丧失,微观机械咬合力参与工作,界面黏结力由机械咬合力和摩阻力构成,点B处黏结应力代表极限黏结强度τu.
滑移段(BC1、BC2、BC3和BC4段):曲线出现4种形状特征,黏结力由机械咬合力和摩阻力构成,滑移段最低点处黏结应力代表残余黏结强度τr.
内配工字型钢的τ-s曲线在滑移段分为Ⅰ-1和Ⅰ-3类,见图5(a)~(b).1)Ⅰ-1类曲线在BC1段下降后保持水平发展,随着工字型钢的推出,嵌含在工字型钢表面的混凝土晶体被彻底剪碎,机械咬合力逐渐减小,曲线呈下降趋势.由于工字型钢表面较为平整,摩擦力在滑移后期不再增大;2)Ⅰ-3类曲线在BC3段迅速下降后仍呈缓慢下降趋势,随工字型钢被推出,部分试件的自由端处混凝土出现局部损伤,导致实际有效黏结面积减小,界面上被剪碎的水泥晶体粉末也被带出,导致摩擦力在后期减小,曲线在滑移段持续下降.
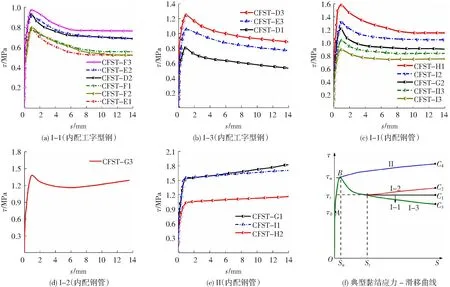
图5 黏结应力-滑移曲线
内配钢管的τ-s曲线在滑移段分为Ⅰ-1、Ⅰ-2和Ⅱ类,见图5(c)~ (e).1)Ⅰ-1类曲线在BC1段下降后保持水平,机理与内配工字型钢相似;2)Ⅰ-2类曲线在BC2段下降后出现二次上升段,由于内配钢管的制作“宏观偏差”不可忽略,其外径沿纵向呈不规则状,导致在推出过程中形成“锥楔作用”,使摩阻力继续增大,进而出现二次上升;3)Ⅱ类曲线在BC4段无下降段,形成拐点B后以较小斜率继续上升,这是因为内配钢管的制作“宏观偏差”程度较大,且远高于Ⅰ-2试件,较强的“锥楔作用”使摩阻力在滑移段早期大于极限滑移荷载Pu,导致曲线持续升高.
根据上述机理分析,可初步认为τ0、(τu-τr)、τr分别为化学胶结力、机械咬合力和摩阻力的比值.由表3可知,内配工字型钢界面黏结力中三部分组成比值均值为1∶0.49∶1.15,内配钢管界面黏结力中三部分组成比值均值为1∶0.40∶1.55,两种钢骨黏结力组成的比重关系均为摩阻力所占比重最大,其次为化学胶结力,最小为机械咬合力.相比文献[12]型钢混凝土界面黏结力中三者比重关系1∶0.14∶0.19,型钢混凝土中摩阻力所占比重大小明显低于内配钢骨钢管混凝土,这与两者在结构上的差异直接关联.相比型钢混凝土中配置的外包箍筋,外钢管提供的横向紧箍作用更高,对内配钢骨残余黏结强度的提高具有显著优势.
3 黏结强度影响因素正交试验分析
正交试验分析方法综合了极差分析和方差分析的优点,两者相互补充.极差分析根据极差Ri的大小,以判别各因素影响结果指标的主次关系及变化趋势.方差分析通过F值与不同置信水平下的Fa临界值进行对比,以判别各因素的显著性影响水平.
3.1 内配工字型钢极限黏结强度
图6为内配工字型钢极限黏结强度τu极差分析结果,由RC1=0.30>RA1=0.14>RB1=0.09可知,影响τu的因素主次关系为:工字型钢截面尺寸(SI)、黏结长度(Le)、混凝土强度(fcu).τu随黏结长度增大而减小,初步分析为黏结长度越大,黏结应力沿界面分布的不均匀程度越大,导致τu降低.当混凝土强度C30增大到C50时,τu整体呈增大趋势,由于工字型钢与混凝土界面密实度随混凝土强度增大而增高,有利于界面黏结性能的提高.而τu随内配工字型钢截面尺寸增大而减小,这是因为外钢管尺寸统一时,管中混凝土保护层厚度随工字型钢横截面尺寸增大而减小,混凝土提供的横向约束作用相应减弱,导致τu显著下降.
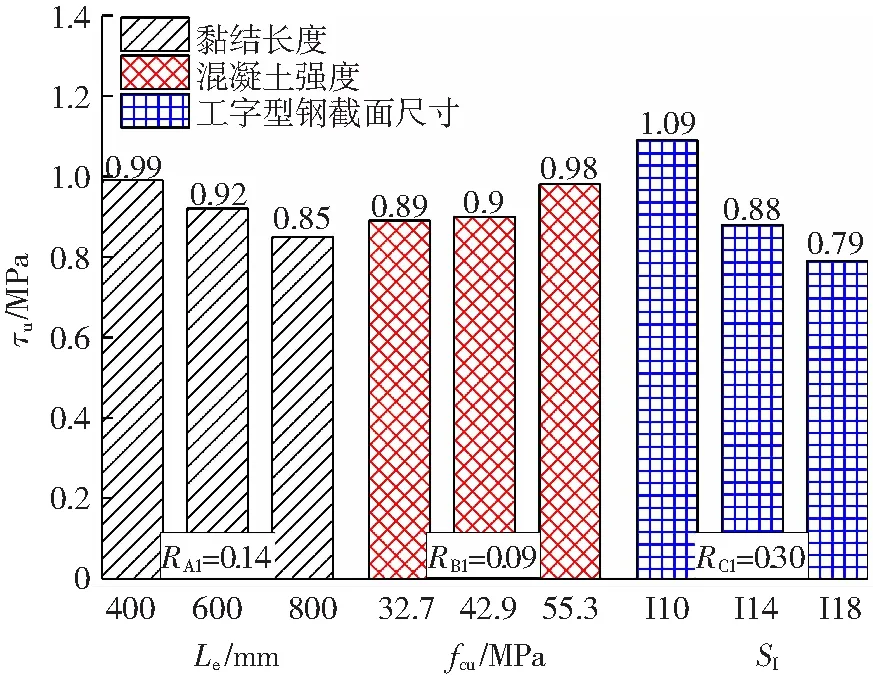
图6 工字型钢极限黏结强度极差分析
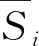
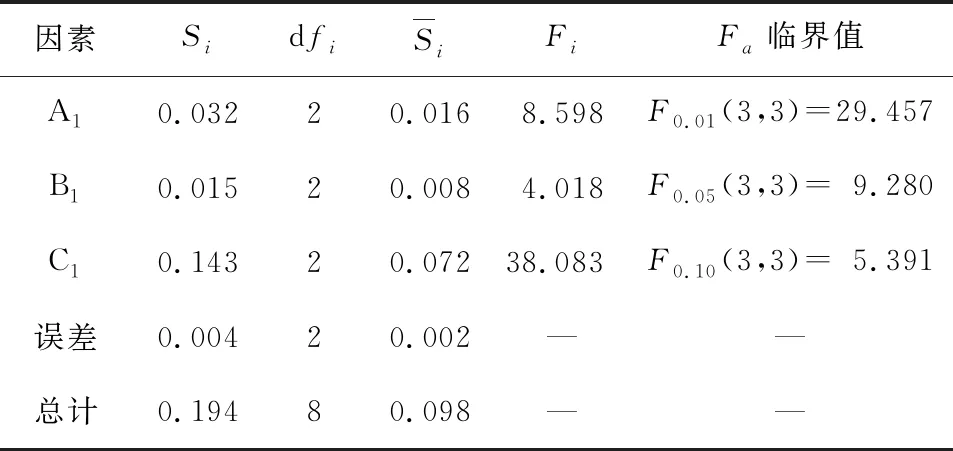
表4 工字型钢极限黏结强度方差分析
3.2 内配钢管极限黏结强度
从图7可知RC2=0.45>RB2=0.26>RA2=0.14,说明影响内配钢管极限黏结强度τu的因素主次关系为:内配钢管截面尺寸(SII),膨胀剂掺量(v),黏结长度(Le).当黏结长度从400 mm增大到800 mm时,τu整体呈下降趋势.τu随膨胀剂掺量增大而增大,因为混凝土的膨胀可有效降低混凝土径向和纵向收缩作用,从而减小对黏结界面造成的不利影响,内配钢管表面受到夹层混凝土膨胀产生的压应力,有利于增强内配钢管界面黏结性能.τu随内配钢管截面尺寸增大而显著减小,由于推出过程中夹层混凝土对内配钢管提供了相应的环向紧箍力,而外钢管型号均为φ299×4.5,随内配钢管直径增大,管中混凝土保护层厚度减小,提供给内配钢管的横向紧箍作用越弱,导致τu显著下降.
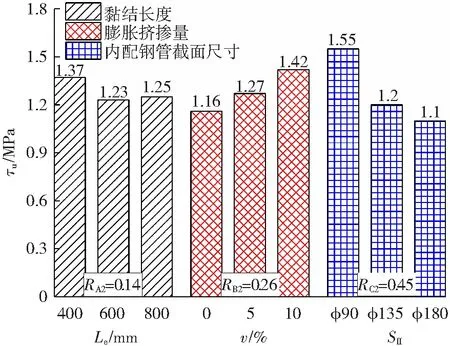
图7 内配钢管极限黏结强度极差分析
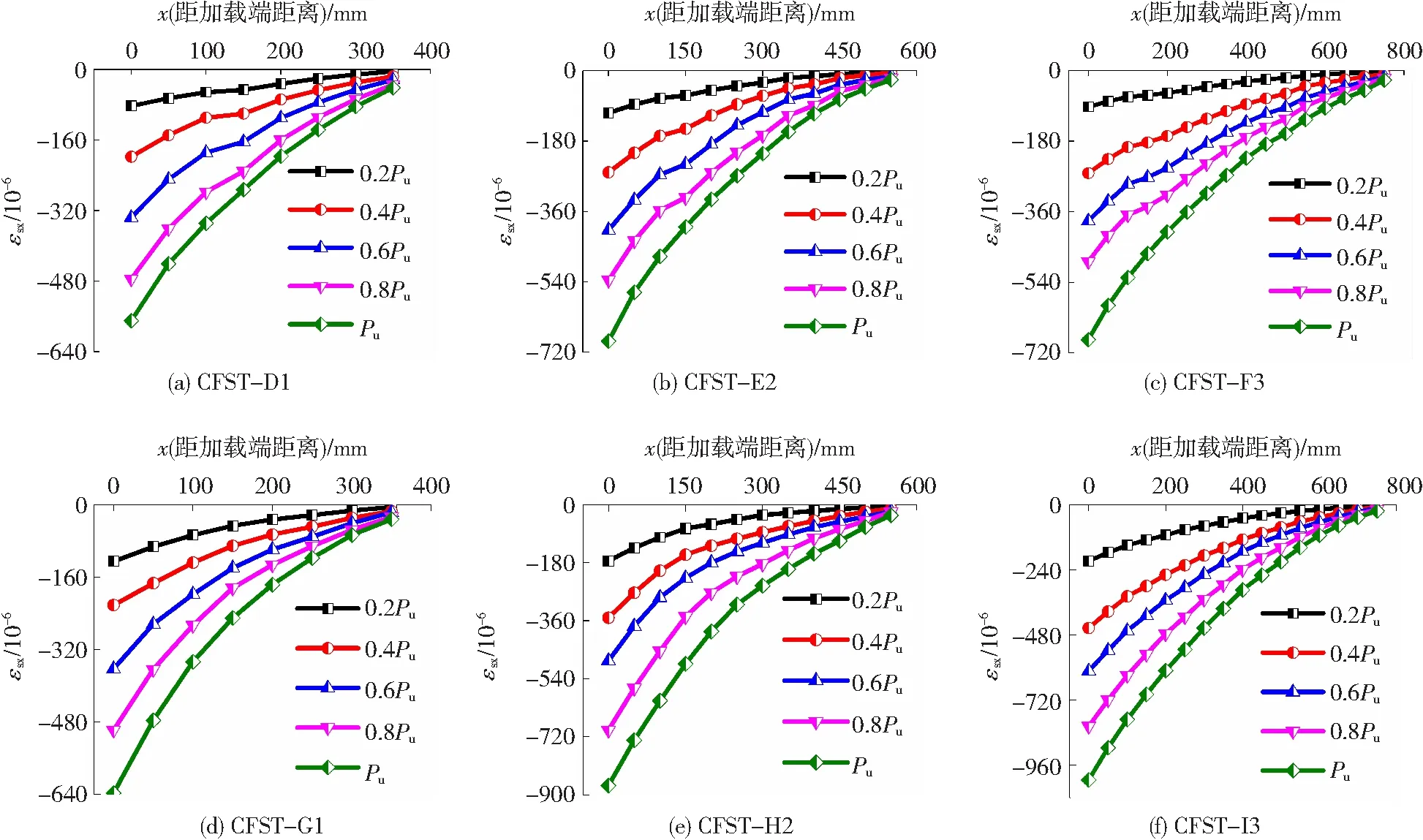
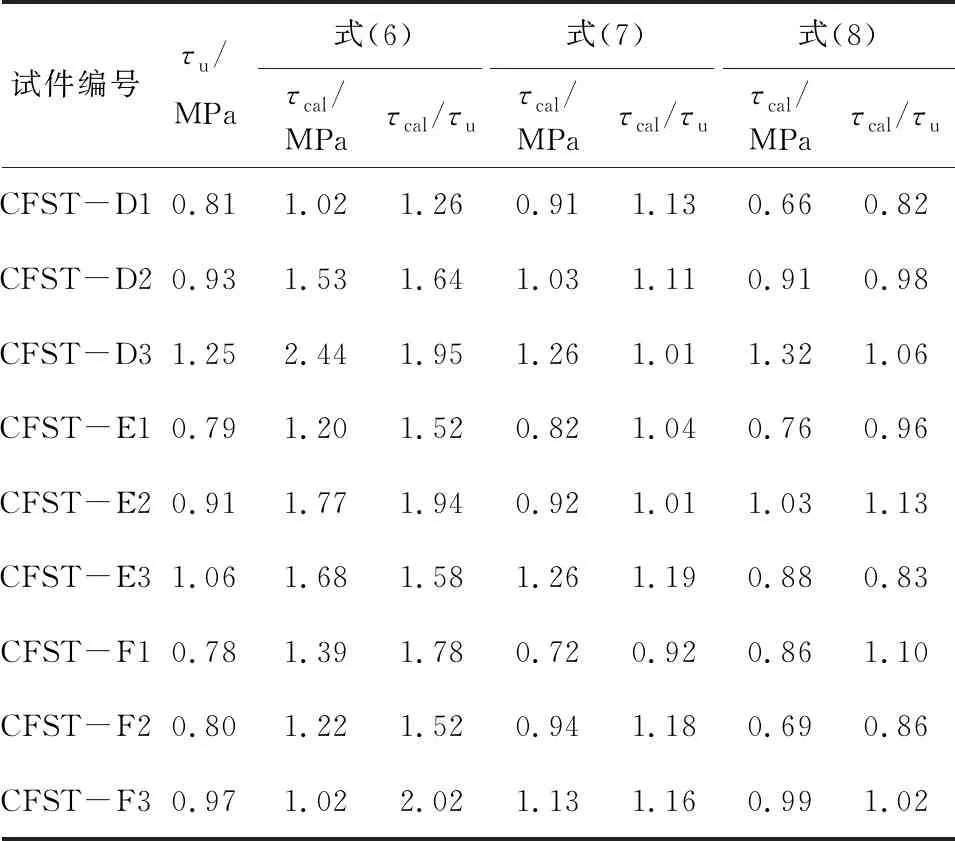
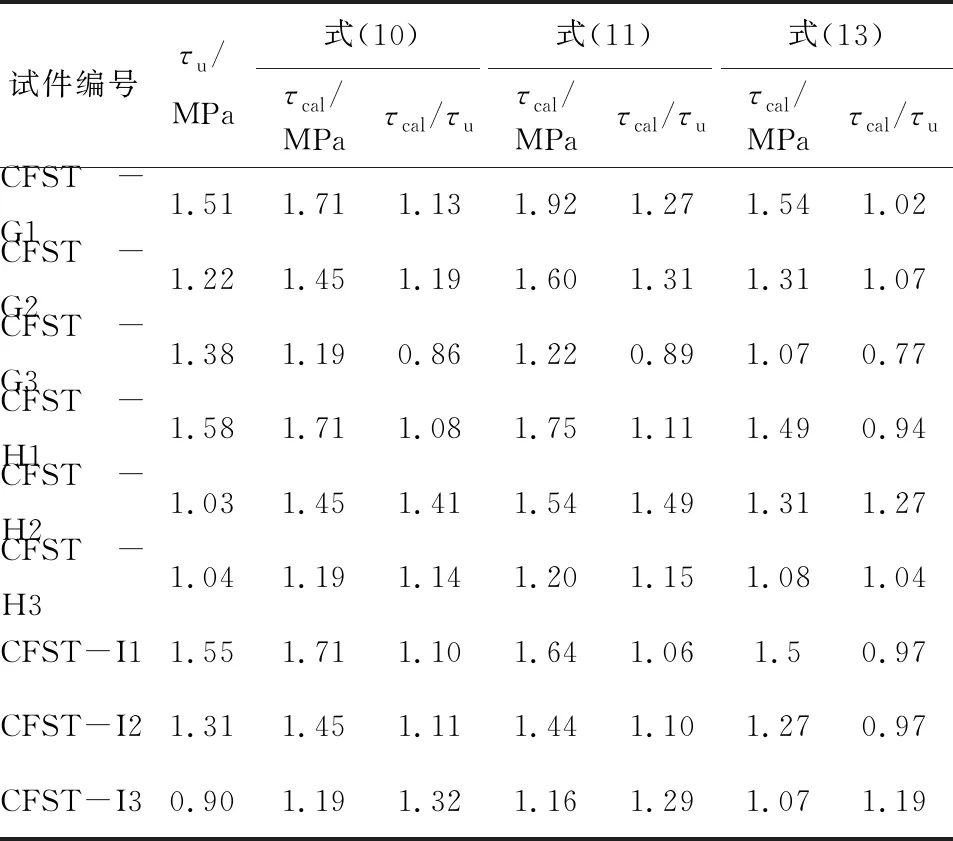
表5为内配钢管极限黏结强度τu方差分析结果,由FC2=20.024>F0.05(3,3),FB2=6.397>F0.10(3,3),FA2=2.040 表5 内配钢管极限黏结强度方差分析 图8为内配工字型钢和内配钢管在20%、40%、60%、80%和100%Pu下纵向应变分布情况.由图8可知,内配工字型钢和内配内配钢管纵向应变的最大值位于加载端附近,距钢骨的加载端越远,纵向应变越小.随荷载增大,自由端应变增幅比加载端明显要小,两端处的纵向应变差逐渐增大,说明施加在钢骨上荷载通过黏结力传递给了外包混凝土.分布曲线整体呈上凸状,曲线斜率逐渐减小,初步分析黏结应力沿黏结长度呈不均匀分布.各级荷载下曲线之间的应变差基本接近,说明推出过程中内配工字型钢和内配钢管一直处于弹性状态. 内配钢骨纵向应变沿黏结长度方向大致呈负指数分布,可表示为 εsx(x)=εmaxe-bx, (2) 式中:εsx(x)为距加载端xmm处的纵向应变,εmax为内配钢骨纵向应变的最大值,b为应变特征系数.采用式(2)中负指数函数对所有典型试件在Pu下纵向应变分布曲线进行拟合.对拟合结果进行统计,b值约为0.003 00~0.006 68,拟合相关系数为0.981~0.994,整体拟合度较好. 图8 纵向应变分布曲线 根据内配钢骨与混凝土微元体受力关系,可得黏结应力τ(x)与钢骨表面纵向应变εsx(x)的一阶微分成正比[11],由式(2)可知,纵向应变εsx(x)呈负指数函数分布,则黏结应力τ(x)可表示为 τ(x)=γiτue-kix, (3) 式中:x为距混凝土加载端距离,τu为极限黏结强度,γi、ki为内配钢骨的黏结应力特征系数. 图9(a)为内配工字型钢在极限滑移荷载Pu下的黏结应力分布曲线.内配工字型钢翼缘外侧和腹板的黏结应力最大值均位于加载端附近,距加载端的距离越远,黏结应力越小.内配工字型钢黏结应力沿纵向呈不均匀分布,主要由工字型钢与混凝土界面的黏结裂缝沿纵向从加载端向下逐步发展引起.对已形成界面黏结裂缝的位置而言,外钢管和混凝土对工字型钢的横向紧箍作用可使黏结应力保持稳定.随荷载增大,黏结裂缝不断沿纵向发展,即将产生裂缝位置的黏结应力开始提高. 采用式(3)中负指数函数对典型试件中内配工字型钢在Pu下的黏结应力分布曲线进行拟合,并对9个内配工字型钢钢管混凝土试件拟合结果进行统计,翼缘外侧平均黏结应力约为腹板平均黏结应力的1.77倍,拟合相关系数为0.715~0.996,拟合度较好.采用origin中的回归分析得到各特征参数的关系式,表达式为 (4) 式中:λ与横截面位置有关,经过回归分析,翼缘外侧和腹板处λ值分别为1和0.56,Pu为极限滑移荷载,C为工字型钢横截面周长,h为工字型钢横截面高度,γ1、k1为内配工字型钢指数特征系数,k1与Le、h、fcu等变化参数有关. 图9 内配钢骨黏结应力拟合曲线 图9(b)为内配钢管在极限滑移荷载Pu下黏结应力分布曲线,内配钢管黏结应力最大值位于加载端附近,距离试件的加载端越远,界面黏结应力越小,曲线整体呈下凹状.采用式(3)中负指数函数对典型试件在Pu下黏结应力分布曲线进行拟合,并对9个圆中空夹层钢管混凝土试件的拟合结果进行统计,拟合相关系数为0.856~0.960,整体拟合度较好.通过回归分析得到各特征参数的关系式,表达式为 (5) 式中:γ2、k2为内配钢管特征系数,其与Le、(D2/t2)、fcu等变化参数有关,D2、t2分别为内配钢管直径和厚度.通过式(3)~(5)的建立,根据极限滑移荷载、试件参数等即可预测沿黏结长度方向任意位置处黏结应力大小. 图10为内配钢骨极限黏结强度与国内外规范对比结果.目前国内外相关规范中仅针对外钢管与混凝土界面黏结强度设计值τd进行了规定,国内的CECS28:2012《钢管混凝土结构技术规程》[20]要求根据混凝土强度等级(C30~C80)进行黏结强度设计值取值,范围为0.4~0.6 MPa,日本规范AIJ[21]规定了圆形钢管混凝土黏结强度设计值为0.225 MPa,英国规范BS540025:2005[22]、澳大利亚规范AS5100.6—2004[23]、美国规范ANSI/AISC360-10[24]规定取值均为0.4 MPa,欧洲规范Eurocode4[25]规定圆形钢管混凝土界面黏结强度设计值为0.55 MPa. 图10 极限黏结强度对比结果 由图10可知,内配工字型钢、内配钢管界面极限黏结强度均值分别为0.919、1.283 MPa,两者均大于国内外相关规程中外钢管与混凝土界面黏结强度设计值τd,Roeder等[26]通过试验研究表明,收缩作为混凝土的变形特性,对外钢管与混凝土界面的黏结十分不利.而内配钢骨钢管混凝土中混凝土的收缩常指向形心处,即内配钢骨表面,明显可促进内配钢骨与混凝土界面的黏结,说明内配钢骨和外钢管在配置方式的差异对界面黏结性能影响显著.通过对比可知,钢管混凝土中内配钢管与混凝土黏结性能明显优于内配工字型钢黏结性能,以上规范均暂未考虑钢管混凝土中内配钢骨的黏结强度设计值,建议相关规范可将内配钢骨钢管混凝土结构的黏结强度纳入考虑. 目前有关钢管混凝土中内配工字型钢与混凝土黏结强度计算方法极少,目前研究主要针对型钢混凝土黏结强度提出了相应的计算式,本文选取了代表性计算式计算本文试件. 文献[6]计算式为 τu=0.082 7ft-0.045 4Le/h+0.862Cs/h+1.029 5. (6) 文献[7]计算式为 τu=ft(0.292 1-0.078 1Le/h+0.459 3Cs/h). (7) 基于本文中9个内配工字型钢钢管混凝土试件实测结果,考虑各因素对极限黏结强度的影响,建立计算式为 τu=ft(0.05t1-0.01Le/h+0.459 3Cs/h). (8) 式中:Cs为混凝土保护层厚度,t1为外钢管厚度,h为工字型钢横截面高度,ft为混凝土抗拉强度,计算式为[27] (9) 表6 内配工字型钢极限黏结强度对比 表6为极限黏结强度实测值与计算值对比结果,采用式(6)计算得到两者比值的平均值为1.691,计算值明显偏大.采用式(7)与式(8)计算得到比值的平均值分别为1.083、0.974,变异系数分别为0.085、0.119,式(8)计算结果与试验结果比较接近,且更加偏于安全、保守,而式(7)无法考虑外钢管的横向紧箍作用,建议采用式(8)用于钢管混凝土中内配工字型钢与混凝土界面极限黏结强度的计算. 为探讨关于钢管混凝土中内配钢管界面极限黏结强度的计算方法,选取以下计算方法进行对比分析. 文献[18]结合16个钢管混凝土中内配钢管推出试验实测结果,采用线性回归,提出了极限黏结强度随内配钢管径厚比变化的计算方法,其计算式为 τu=2.229-0.026D2/t2, 0 (10) 英国健康与安全执行局在《Pile/sleeve connections: offshore technology report》[28]中提出了套管桩内部黏结力的计算方法,可用于钢管混凝土中内配钢管与混凝土界面极限黏结强度计算,其表达式为: (11) K=[m(D1/Cs)]-1+[(D2/t2+D1/t1)]-1. (12) 式中:m为钢管与混凝土弹性模量之比;fcd为混凝土圆柱体抗压强度;D1、t1分别为外层钢管直径和厚度;D2、t2分别为内配钢管直径和厚度;Cs为混凝土保护层厚度;CL为黏结长度系数,当Le/D2=2时,CL取1,当Le/D2=12时,CL取0.7,其余CL取插值;Cm为界面系数,受压时Cm取0.6,受拉时Cm取0.3. 本文在以上计算方法基础上,考虑各因素对极限黏结强度的影响,结合9个圆中空夹层钢管混凝土中内配钢管的推出试验实测结果,提出极限黏结强度计算式为 τu=0.166ft(0.058D1/t1-0.044D2/t2-0.014Le/D2). (13) 由表7可知,采用式(10)、(11)得到的极限黏结强度计算值与实测值比值的均值分别为1.149、1.186,变异系数分别为0.134、0.149,两者均比试验结果略偏高.采用式(13)得到的极限黏结强度计算值与实测值比值的平均值为1.028,变异系数为0.140,误差较小,拟合公式更为精确,说明式(13)可用于钢管混凝土中内配钢管与混凝土界面极限黏结强度的计算. 表7 内配钢管极限黏结强度对比 根据9个内配工字型钢钢管混凝土试件和9个圆中空夹层钢管混凝土试件的推出试验结果,对两种内配钢骨与混凝土黏结性能进行了分析,可得到以下结论: 1)两种钢骨黏结应力-滑移曲线均包括胶结段、非线性初滑移段和滑移段.由于直缝焊接钢管存在不同程度制作“宏观偏差”,曲线在滑移段出现下降后水平、持续下降、下降后二次上升和持续上升等4种趋势.两种钢骨界面黏结力中摩阻力所占比重最大,其次为化学胶结力,最小为机械咬合力. 2)影响内配工字型钢极限黏结强度τu的因素主次关系为工字型钢截面尺寸、黏结长度、混凝土强度.τu随工字型钢截面尺寸和混凝土强度增大而增大,随黏结长度增加而有所减小.影响内配钢管极限黏结强度τu的因素主次关系为内配钢管截面尺寸、膨胀剂掺量、黏结长度;τu随内配钢管截面尺寸和膨胀剂掺量增大而增大,随黏结长度增大,τu先降低后有所增大. 3)峰值荷载下内配工字型钢和内配钢管黏结应力沿黏结长度均呈负指数函数分布,内配工字型钢黏结应力沿截面周长方向分布不均匀,翼缘外侧黏结应力约为腹板的1.77倍. 4)钢管混凝土中内配钢管黏结性能优于内配工字型钢黏结性能.基于推出试验实测数据,建立了钢管混凝土中两种内配钢骨的极限黏结强度经验计算式,与其他学者计算方法的对比证明本文计算式有较好适用性.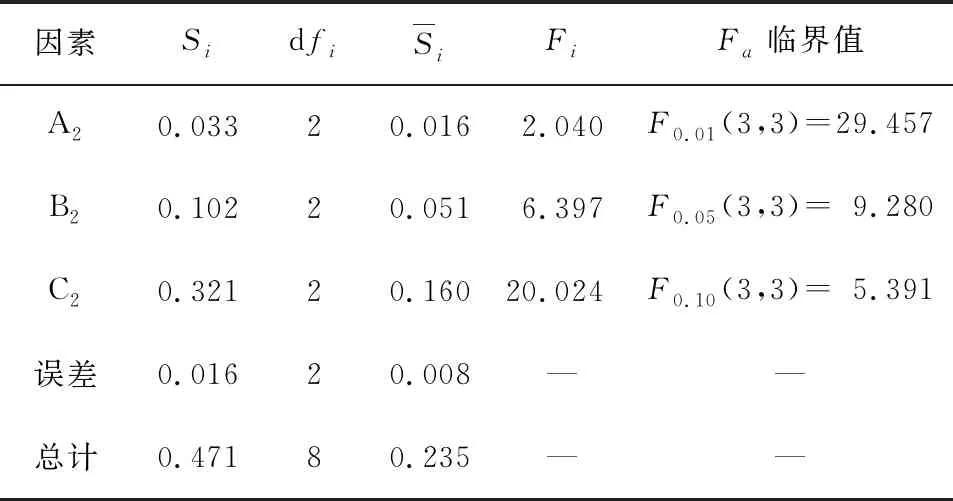
4 内配钢骨纵向应变分布曲线
5 内配钢骨黏结应力分布规律

6 黏结强度计算方法
6.1 黏结性能对比分析

6.2 内配工字型钢极限黏结强度计算
6.3 内配钢管极限黏结强度计算
7 结 论
