不同温度下砂岩渗透性能的核磁共振响应

2020-07-22邵继喜胡耀青刘志军靳佩桦

太原理工大学学报 2020年4期

邵继喜，胡耀青，刘志军，靳佩桦

(1.广州市建筑科学研究院有限公司广州市市政工程试验检测有限公司，广州 510520；2.华南理工大学土木与交通学院，广州 510641；3.太原理工大学采矿工艺研究所，太原 030024；4.黑龙江科技大学矿业工程学院，哈尔滨 150022)

在地热利用及煤炭地下气化等资源开发过程中，储层的渗透性能对于流体的开发至关重要[1]，也是判定储层开采价值的重要指标之一。在温度作用下，岩石内部结构会发生变化，在矿物脱水、相变等物理化学作用的综合效应下[2-3]，孔裂隙形态会发生变化，导致岩石的渗透率发生改变。

国内外学者对温度影响下岩石渗透率做了大量研究，梁冰等[4]采用理论分析与实验结合的方法，得出了岩石渗透率与温度呈指数关系，并证明了温度阈值的存在。刘均荣等[5]对高温作用后岩石渗透的变化机理进行探讨，得出了渗透率随温度的升高而呈增大趋势的结论；同时认为，岩石渗透率存在阈值温度，岩石组分不同，其阈值温度有差异。其他学者对多场耦合作用下温度对渗透率影响的机理进行了研究[6-12]，得出了不同温度条件下渗透率变化特征。总体上看，岩石材料随温度变化会导致其物理化学性质的改变，温度作用后，渗透率随多孔介质的变化而变化。以往的研究多建立在大量重复性的实验基础上，虽然能保证实验结果的准确性，但相应地耗费了较多的人力、物力，而测试手段的优化将解决这些问题。

近年来科学技术迅速发展，核磁共振技术(NMR)以测试方法的“原位性”和“完整性”等优势而得到广泛应用[13-16]。通过核磁共振弛豫效应来获取岩石孔隙分布及孔隙结构特征、渗透率、流体性质及含量等信息，该技术已经成为了岩心物性分析的新手段[17]。XIAO et al[18]利用NMR技术对松辽盆地致密砂岩进行研究，对多尺度孔隙进行分类，并对致密砂岩孔隙度和渗透率的关系进行探讨。目前，多数的研究都集中在常温岩石领域，利用NMR技术对高温作用后岩石渗透性能的研究较少。因此，本文在前人研究的基础上，采用低场核磁共振技术对不同温度作用下砂岩渗透性能进行研究，以期为地下深部流体开发提供理论借鉴。

1 核磁共振基本原理

NMR岩心物性分析主要是测量岩石孔隙中含1H流体的弛豫特征。对于不同属性的样品，其能量释放速度有差异，通过这些信号差别就可以直观反映岩石孔隙结构的变化特征[13]。通过对完全饱和水的岩心进行CPMG脉冲序列测试，得到自旋回波串的衰减信号，其信号是不同大小孔隙内水信号的叠加。自旋回波串衰减的幅度可以用一组指数衰减曲线之和来进行精确地拟合，每个指数曲线都有不同的衰减常数，所有衰减常数的集合就形成了横向弛豫时间t2分布[17]。

NMR弛豫时间(t2)由表面弛豫(t2S)、体弛豫(t2B)和扩散弛豫(t2D)组成的。t2B时间远大于t2，计算时可忽略。采用均匀磁场进行NMR实验时，t2D也能忽略。因此，孔隙大小和t2时间之间可表示为：

(1)

式中：S为孔隙表面积，m2；V为孔隙的体积，m3；ρ2为横向表面弛豫强度，m/s.对于储层流体而言，弛豫时间与其所在的孔隙结构(S/V)有关。当孔隙越小时，其比表面积越大，孔隙表面与水的作用越强，使得其中水弛豫速率越快，弛豫时间越短[19]。因此，可依据核磁共振t2谱获得样品孔径分布、岩芯孔隙度、t2几何均值等参数。

2 实验

2.1 样品描述

岩样取自山西省大同市某矿山，为中细粒石英砂岩，呈深灰色，块状构造，中细粒砂状结构。石英质量分数为60%～65%，以单晶石英为主。长石质量分数为1%～5%，以斜长石为主，少见钾长石。充填物为黏土杂基、钙质胶结物、白云质胶结物，质量分数为30%～35%。

2.2 实验步骤

1) 将现场采集的样品用聚氯乙烯薄膜封装处理，运至实验室后即进行切割处理。为了保证实验结果的准确性，所有的样品均取自同一块完整砂岩，然后利用小型岩样取芯机将样品加工成Φ1 cm×2.5 cm圆柱体小件，以满足核磁共振实验要求。

2) 将试样置于高温加热炉中，然后以5 ℃/min的速率加热至目标温度(25，200，400，600 ℃)，将样品在目标温度中保持4 h，然后以相同的速率(5 ℃/ min)将炉子冷却至室温，以保持样品中的温度均匀分布，并且在加热和冷却期间避免热冲击，然后对冷却样品进行核磁共振实验。

3) 采用MicroMR12-025V NMR波谱仪进行砂岩NMR分析。回波间隔时间为0.1 ms，等待时间为2 000 ms，回波数为4 000，扫描数为128. NMR实验前，将不同温度的砂岩置于真空干燥箱常温下干燥24 h.待干燥和抽真空后，称量干燥样品的重量。将样品放入真空饱和装置以达到完全饱水状态。称量饱水样品重量从而获得饱水孔隙度，然后进行饱水样品的NMR测试获得样品t2谱值，随后测试样品离心状态下的t2谱值。

3 结果与分析

3.1 孔隙度及t2几何均值确定

由于核磁信号幅度与砂岩样品所含的氢核数目呈正比，因此可用NMR的t2谱来计算孔隙度[15]。但是标定过程较复杂，理论上称重法所得的饱水孔隙度等同于NMR孔隙度(φNMR).一般基于NMR孔隙度(饱水孔隙度)结果，将NMR孔隙度划分为可动水孔隙度(φF)和束缚水孔隙度(φB)[15]，可以表示为：

(2)

(3)

式中：φNMR为核磁孔隙度(饱水孔隙度)，%；FFI为可动流体饱和度，%；BVI为束缚流体饱和度(100-FFI)，%；φF是可动流体孔隙度；将饱水和离心状态下的t2谱转化为饱水和离心状态下的累计孔隙度，如图1所示。所得孔隙度分别对应于(BVI+FFI)总孔隙度(φNMR)和FFI孔隙度(φF).BVI孔隙度(φF)则等于φNMR与φF之差。根据公式(2)、(3)可得不同温度下的砂岩NMR孔隙度参数，见表1.

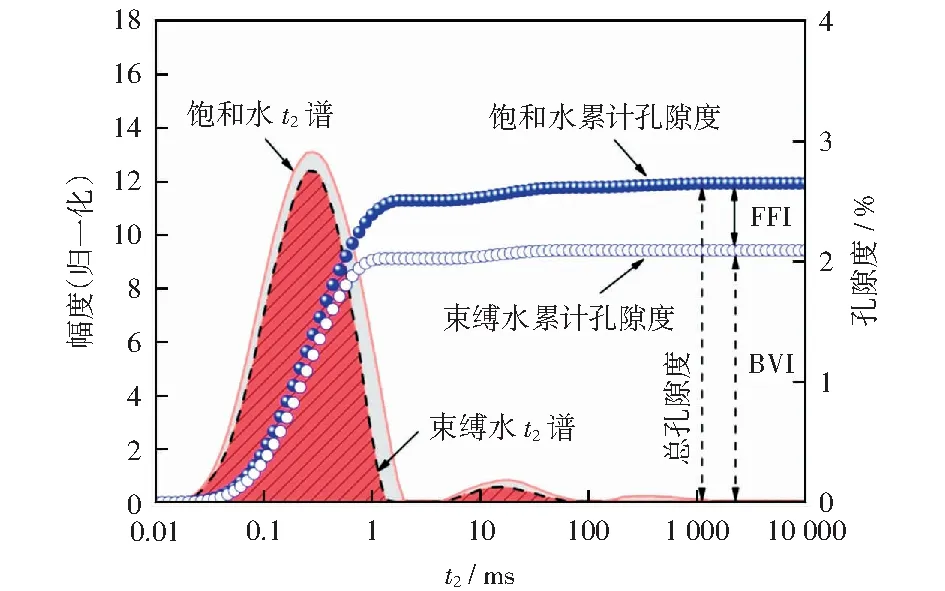
图1 砂岩饱和水和束缚水t2谱及FFI和BVI的求取方法Fig.1 t2 spectrum of saturated water and bound water in sandstone, and methods for obtaining FFI and BVI

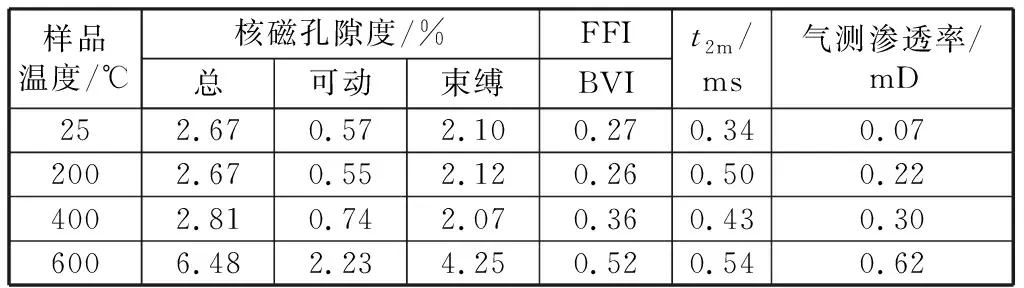
表1 不同温度下砂岩NMR孔隙参数及气测渗透率Table 1 NMR pore parameters and gas permeability of sandstone at different temperatures

3.2 渗透率模型参数计算及选取

渗透性提供了多孔介质是流体输送能力的指标，是评价储层生产能力的关键[20-21]。国内外学者已经利用低场核磁共振技术做了大量的岩心渗透率的研究。采用核磁共振的方法确定孔隙度和可动流体含量参数后，建立了核磁渗透率与核磁共振t2几何平均值、核磁孔隙度和可动流体等参数的定量关系。目前应用的核磁共振岩心分析模型主要有以下几种[20-22]：

Coates(自由流体模型)模型为：

(4)

改进的Coates模型为：

(5)

SDR模型(也称为平均t2模型)为：

(6)

改进SDR模型可以表达为：

(7)

PP模型(也称为可动孔隙度模型)可以表达为：

K5=A5×exp(φF/a3)+b3.

(8)

式中：K1、K2、K3、K4、K5是这5个方程的核磁共振渗透率，mD；A1、A2、A3、A4、A5和a1、a2、a3、b1、b2、b3是与岩石特征相关的未确定系数；t2m为饱和水条件下t2分布的几何平均值，ms.

将表1所得实验结果分别代入公式(4)-(8)，进行迭代计算，分别求出各公式的参数值，为简化计算过程，将计算后所得参数结果整理见表2.

将表2参数分别代入渗透率模型公式(4)-(8)，然后将不同温度下孔隙参数代入整理后的公式，进行渗透率计算，结果见表3.

表2 核磁渗透率模型参数Table 2 Nuclear magnetic permeability model parameters

依据表3结果可知，SDR模型与改进的SDR模型，同Coates模型、改进Coates模型、PP模型和实测气体渗透率相比，SDR模型及其改进SDR模型可用于评估渗透率。在25～600 ℃的温度区间内，5种模型所得渗透率结果都随温度的升高而增加，但是在具体的温度范围内，不同的模型估算所得的渗透率存在较大差异。具体表现为：在25～400 ℃温度范围内，Coates模型和改进Coates模型与实测渗透率相比，测试结果较低，增长趋势平缓，与实测渗透率随温度变化趋势不符(见图2)，说明这两个模型不适合估算不同温度下的渗透率。已有研究表明，当渗透率低于0.1 mD时PP模型估计的误差较大[20]，这与本文研究结果相同。如在25 ℃时，PP模型的预测渗透率为实测渗透率的2.93倍，偏差较大。此外，PP模型需要大量数据构建，使用起来不方便[20]。而对于所选改进SDR模型而言，预测渗透率虽然准确，但需要3个参数进行表征，相比SDR模型较为繁琐。通过以上分析表明，使用SDR模型比其他模型更方便。因此，本文采用SDR模型预测不同温度下渗透率变化。

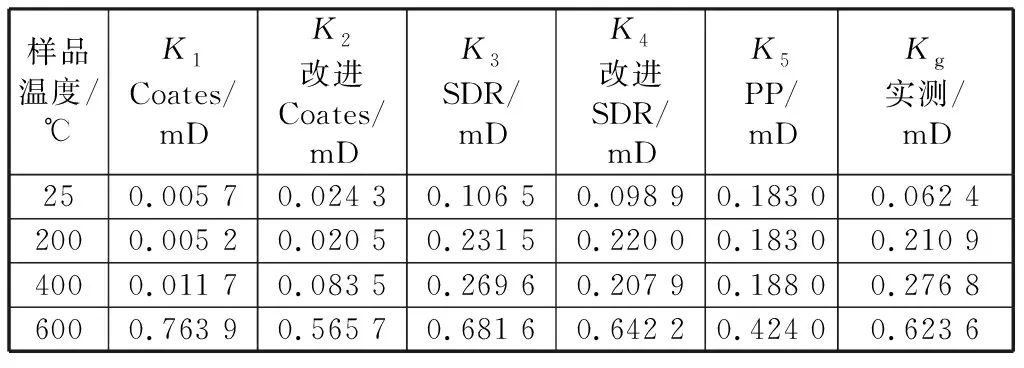
表3 核磁共振渗透率计算不同模型和气体渗透率测量Table 3 Calculation of NMR permeability with different models and gas permeability measurements

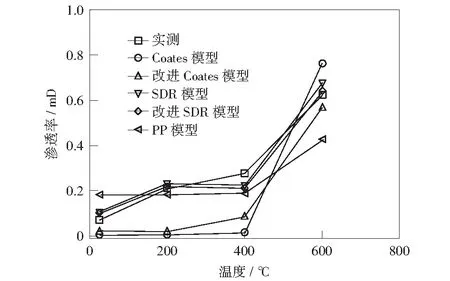
图2 各渗透率模型随温度变化关系Fig.2 The permeability model’s relationship with temperature

图3为基于SDR模型的NMR渗透率与温度关系图，因此，NMR渗透率与温度的关系可以拟合为：

KNMR=1.05×10-8t3-7.99×
10-6t2+0.002t+0.060 5 .

(9)

式中：KNMR为砂岩NMR渗透率，mD；t为温度，℃.依据本公式可以预测25～600 ℃温度范围内砂岩的渗透率。

3.3 核磁共振渗透率分析

为了验证公式(9)的准确性，本文将表征后的NMR渗透率与梁冰等[4]研究的阜新砂岩、游利军等[23]研究的四川砂岩渗透率结果进行对比。考虑到实验条件不同(地质赋存条件、所含矿物种类、加热方式等)，这里只讨论变化趋势，不考虑渗透率数值的大小。由图4分析可知，在25～600 ℃温度范围内三种砂岩渗透率具有相近的变化趋势，在400 ℃以前，渗透率缓慢增加，大于400 ℃以后渗透率快速增长。三者具有明显的共性，温度突变的拐点基本相同，变化趋势相同。因此，由3种方式所测渗透率对比可知，公式(9)预测砂岩渗透率是准确的，利用NMR技术预测砂岩渗透率方法可靠。

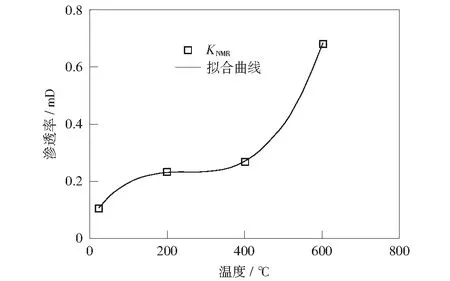
图3 SDR模型渗透率与温度关系拟合Fig.3 The relationship between SDR model permeability and temperature

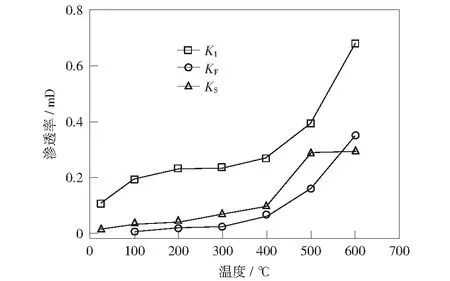
注：K为砂岩NMR渗透率；KF为阜新砂岩渗透率；KS为四川砂岩渗透率图4 NMR渗透率与阜新砂岩、四川砂岩渗透率对比Fig.4 NMR permeability comparison with the permeability of Fuxin sandstone and Sichuan sandstone

许多研究表明，热处理会导致岩石性质劣化，渗透率也发生相应改变[23-24]。除了外部应力，热膨胀和矿物热反应这两个关键因素控制岩石渗透率在高温下的变化。前者可能由于矿物的热膨胀特性的差异而诱发大的内部热应力，导致热破裂[4]。同时，矿物热反应可能产生一些新的矿物出现，堵塞渗流通道[25-26]。由本文研究可知温度引起φNMR增加的同时，φB和φF也具有相同变化趋势。然而，φB和φF的变化幅度是不同的。相比25 ℃，400～600 ℃温度范围内φB增加了0.98～2.02倍，而φF增加了1.29～3.91倍，可动水孔隙度增加幅度要大于束缚水孔隙度增加幅度，揭示了由温度引起的孔裂隙系统变化在不同尺度上表现不一。这意味着温度对φF的影响大于对φB的影响，岩石受热应力及物理、化学作用的影响，大量的孔裂隙产生是差异出现的主因。此外，温度对孔隙连通性的变化起控制作用，孔隙连通程度具有阶段性特征，温度低于400 ℃时，孔隙间连通性较差，此温度范围内温度升高并不能有效促进孔隙间的连通性能；温度大于等于400 ℃时，孔隙连通性得到改善，连通性能明显提高。

孔隙度变化会引起渗透率的改变，由图4可知渗透率与温度增长是一个非线性增长过程，存在突变的阈值温度点，本实验的阈值温度点为400 ℃.岩石由于矿物种类不同、组分差异，渗透率阈值温度点也不同。由前文分析可知，这种差异有时候是显著存在的。