考虑应变率效应的碳纤维增强复合材料发动机罩行人保护分析

2020-07-22程超汪霞

汽车技术 2020年7期

程超汪霞

（泛亚汽车技术中心有限公司，上海 201201）

主题词：碳纤维增强复合材料应变率行人保护发动机罩

1 前言

碳纤维增强复合材料（Carbon Fiber Reinforced Polymer，CFRP）具有极高的比刚度、比强度，同时具有良好的抗疲劳性能和碰撞性能，已被大量应用于航空、航天、国防军工等领域。近些年，汽车轻量化的需求越来越高，CFRP作为一种轻量化效果明显的材料，国内部分厂商已对其在汽车外覆盖件上的应用进行了一定的研究[1]。

为了研究CFRP的应变率效应，研究人员分别从不同角度开展了大量工作。周元鑫对T300和M40J 2种碳纤维束实施了应变率范围0.001～1300 s-1的静、动态拉伸试验，结果表明，2种纤维束的弹性模量、拉伸强度以及失稳应变在上述应变率范围内均未发生明显变化，故认为这2 种纤维束是与应变率无关的材料[2]。Amos Gilat 对树脂977-2 分别在0.000 05 s-1、1 s-1和400 s-13种应变率下进行了拉伸试验，结果表明，树脂977-2 是一种与应变率相关的材料[3]。王正浩对2种铺层角度的碳纤维增强复合材料层合板T300/Epoxy 分别在中应变率（1～10 s-1）和高应变率（100～10 000 s-1）下使用少量样件进行了拉伸试验，结果表明，T300/Epoxy 层合板是应变率相关材料[4]。

文献[5]研究了材料应变率对汽车碰撞性能的影响，结果表明材料的应变率对整车碰撞性能的主要参数有较大的影响，考虑材料应变率效应的仿真结果与试验结果比较接近[5]。根据行人保护法规的规定，碳纤维发动机罩需满足行人头部保护的性能要求。但在0～400 s-1的应变率范围内，CFRP 层合板力学性能相关的研究文献较少，且其结论并不明确。为了研究车用CFRP 层合板在高速冲击荷载作用下的应变率效应，本文以某CFRP 发动机罩的T300/Epoxy 典型铺层层合板为研究对象，应用高速拉伸试验机进行0～500 s-1应变率下的拉伸试验，建立T300/Epoxy CFRP 层合板考虑应变率效应的广义Maxwell 本构模型，再将该模型引入有限元分析软件LS-DYNA，对CFRP发动机罩进行行人保护性能仿真与试验，研究CFRP层合板应变率效应对行人保护性能的影响。

2 试验概况

2.1 样条设计

参考ASTM D3049[6]和ASTM D3518[7]2 个标准设计了拉伸性能和面内剪切性能的测试样件，如图1 所示。通过优化加强片长度和锥面角度保证样件在静态拉伸试验时开裂位置出现在有效段，样件尺寸如表1、表2所示。

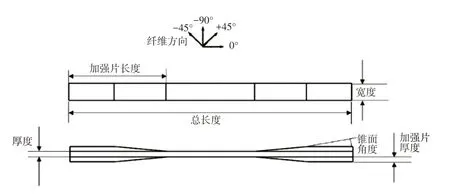
图1 试验样件式样

表1 拉伸性能试件尺寸

表2 面内剪切性能试件尺寸

2.2 数字图像相关技术测试系统

应力-应变曲线的提取使用数字图像相关（Digital Image Correlation，DIC）测试技术，其基本原理是利用物体变形前、后的数字图像得到物体变形过程中的位移和应变云图。DIC测试系统具有非接触、全场、全过程、对环境要求低等优点，该系统主要由图像采集、数字图像分析、加载系统组成，如图2所示。

图2 DIC测试系统

2.3 试验矩阵设计

为了建立T300/Epoxy CFRP 层合板的粘弹性本构模型，在0.01～500 s-1的应变率范围内设计了5组面内剪切拉伸试验以获取剪切模量的松弛模量和衰减常数，2组拉伸性能试验用于对标验证获取的松弛模量和衰减常数是否准确，基于以上需求，设计了高速拉伸试验矩阵如表3所示。

表3 试验矩阵

2.4 试验数据处理

如图3 所示，在试验时保证在每个应变率下获取5组应力-应变曲线的有效样本。

模量提取的应变范围参考ASTM D3518 选取2×10-3～5×10-3。在模量提取后，分别对每批样件计算模量的平均值作为有效数据，同时输出样本的标准差和离散系数，衡量测试数据的波动率：

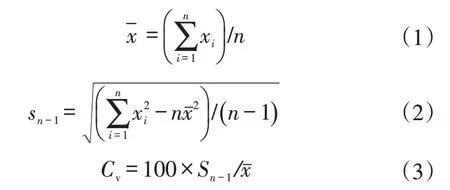
式中，xi为样本值；n为样本数量；-x为样本的平均值；sn-1为样本的标准差；Cv为样本的离散系数。

图3 高速拉伸面内剪切样件失效示意

3 试验数据分析

3.1 面内剪切应力-应变曲线结果分析

面内剪切试验数据经过处理后，得到如图4所示的不同应变率下的应力-应变曲线，曲线处理后得到的剪切模量如图5所示。

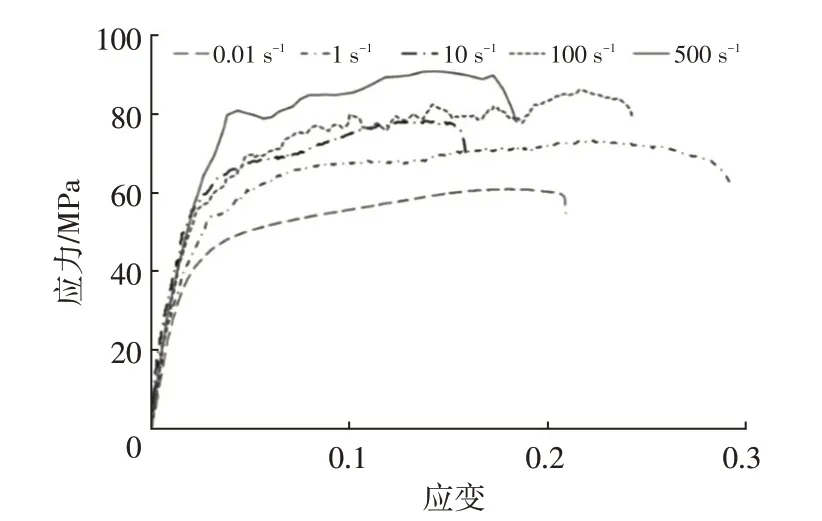
图4 不同应变率下高速拉伸面内剪切应力-应变曲线

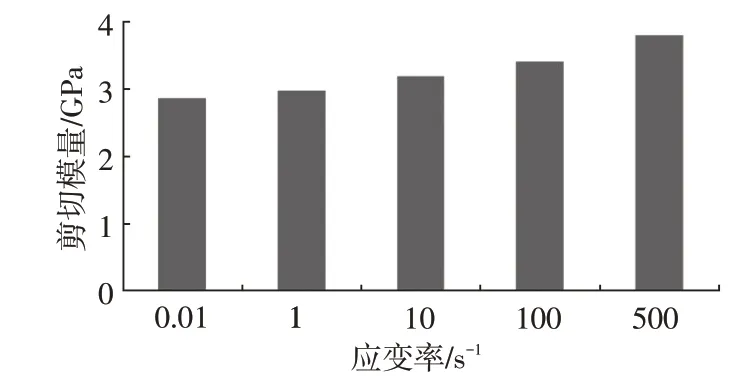
图5 不同应变率下的剪切模量

从图4 可以看出，相同应变下，失效应力随应变率的升高而增大。从图5 可以看出，随着应变率的升高，其初始剪切模量也不断增大。因此，T300/Epoxy CFRP层合板剪切力学性能表现出了明显的应变率相关性。

3.2 拉伸应力-应变曲线结果分析

拉伸试验数据经过处理后，得到0.01 s-1和400 s-1应变率下的拉伸应力-应变曲线，如图6所示。

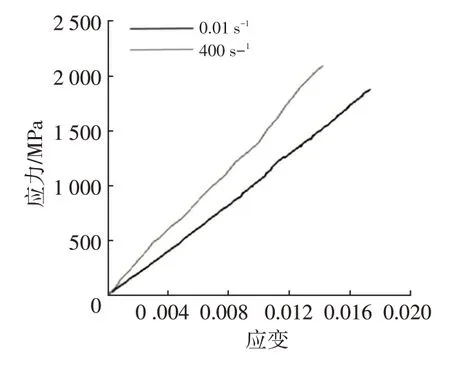
图6 拉伸应力-应变曲线

从图6 中可以看出，随着应变率的升高，其弹性模量随之增大。因此T300/Epoxy CFRP 层合板拉伸力学性能也表现出了明显的应变率相关性。

4 粘弹性本构模型的建立

本文研究的某碳纤维发动机罩在行人保护试验过程中没有出现屈服、断裂等强度失效现象，因此本文主要针对模量的应变率效应进行研究。

4.1 广义Maxwell模型

粘弹性力学中的Maxwell模型是描述应力松弛现象的常用模型，由线性弹簧和牛顿粘壶串联组成。该模型的微分关系为：

式中，σ为应力；η为粘性系数；E为弹性模量；ε为应变。

记θ=η/E，具有时间量纲，通常称为松弛时间。该模型只能给出具有单一松弛时间的响应，在恒应变应力松弛的条件下Maxwell单元的应力解为：

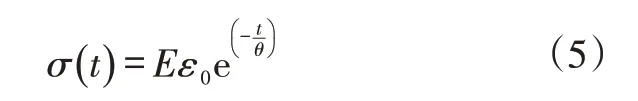
式中，ε0为初始应变；t为时间。

但是单一的Maxwell 单元模型只有1 个松弛时间，应变率变化范围较大时不能描述各应变率下的松弛特性，而多个Maxwell 单元并联组成的广义Maxwell 模型可以用来模拟复杂的应力松弛特性，如图7所示。

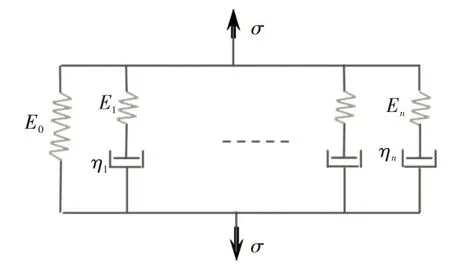
图7 广义Maxwell模型

在小应变理论下，根据广义Maxwell模型的思想，各向同性的线性粘弹性本构方程可以简化为：

式中，τ为积分变量；G(t)为松弛核函数，等于单位总应变所对应的应力，可用PRONY多项式级数形式表示：

式中，E0为初始弹性模量；Ei为松弛模量；βi=ηiEi为松弛模量对应的衰减常数；ηi为粘性系数。

对于单向铺层的层合板，根据横观各向同性材料的公式，有：

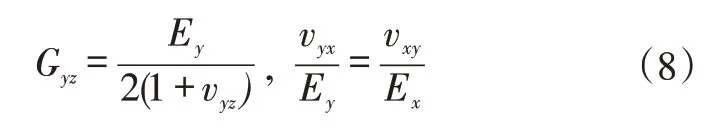
式中，Gyz为面外剪切模量；Ex为轴向弹性模量；Ey为横向弹性模量；vyz、vxy、vyx为泊松比。

根据式（8）可推导出：

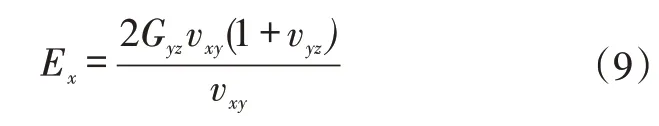
假设式（9）中泊松比没有应变率效应，则有：

对于单向铺层层合板，其面内剪切模量主要体现树脂的材料特性，与面外剪切模量一致，假设其具有同样的应变率效应，则式（10）可以改写为：

式中，Gxy为面内剪切模量。

4.2 本构模型参数获取与验证

文献[8]研究了粘弹性本构模型需要使用的Maxwell元件的数量，模型预测与试验数据对比结果表明，描述类似材料应变率相关性的力学特性Maxwell元件的最小值为4个，因此，本文选择使用5个Maxwell 元件建立本构模型。

利用第4.1节中所述的不同应变率下的剪切模量进行Prony 多项式级数拟合[9]，得到5 个Maxwell 元件下的Prony多项式系数，如表4所示。

表4 Maxwell模型剪切松弛模量和相应的衰减常数

通过表4 得到的Prony 多项式级数分别计算0.01～500 s-1应变率下的5个剪切模量，与试验值进行对比，结果如图8所示。从图8可以看出，预测值与试验值的最大误差在5%以内。

图8 剪切模量预测值与试验值对比结果

根据式（11）可以推导出Maxwell模型弹性松弛模量和相应的衰减常数，如表5所示。

表5 Maxwell模型弹性松弛模量和相应的衰减常数

试验得到的初始弹性模量为103.7 GPa，通过表5得到的Prony多项式级数计算得到400 s-1应变率下的弹性模量为132.0 GPa，而试验值为130.9 GPa，误差在1%以内，Maxwell模型的拟合精度较高，也验证了式（11）所作假设的合理性。

5 发动机罩行人保护性能的分析对标

发动机罩外板由3K 斜纹布和T700 系列12K 单向带组成，3K 斜纹布作为外观层。在建模时使用壳单元模拟，基于*PART_COMPOSITE对发动机罩进行碳纤维复合材料的铺层，共为7 层，每层的角度分别为0°、0°、90°、0°、0°、90°和0°，各层厚度均为0.22 mm。发动机罩内板的处理方式与外板类似。加强板为钢板，建模时使用壳单元模拟，中间的结构胶将内外板与加强板连接在一起，使用实体单元模拟。试验台架使用一维梁单元建立简化模型，在其接地的一端施加约束，另一端通过刚性单元分别与复合材料发动机罩的铰链、锁、缓冲块连接，如图9所示。

为了研究应变率效应对行人保护性能的影响，建立了2 个分析模型，仿真模型1 复合材料使用MAT 58，仿真模型2复合材料使用MAT 158。2个模型的材料基础参数一致，仿真模型2 的MAT 158 材料使用表5 中的Maxwell模型弹性松弛模量和相应的衰减常数。

图9 行人保护头部冲击分析与试验对标

考虑到成人头部和儿童头部的差异，在发动机罩中选取了4个冲击点，其中PC1400301、PC1400304为成人头部，PC1400309、PC1400316 为儿童头部，试验和分析的结果如表6所示。对表6中的对标数据进行分析可以发现，使用不考虑应变率效应的材料参数分析得到的头部损伤评价标准（Head Injury Criteria，HIC）值的平均对标精度只有27%，而使用考虑应变率效应的粘弹性材料本构模型分析得到的HIC值平均对标精度达到78%。