包含序列的一些计算公式和同余式1

李桂贞

（惠州学院 数学与统计学院， 广东 惠州 516007）

Sun[1-2]定义了类似于Euler数｛En｝和Euler多项式｛En( x) ｝的序列｛Un｝和｛Un( x) ｝：

其中，［x］是指不超过x的最大整数. 易知， U2n-1= 0 (n ≥ 1 )．

1 需要用到的定义

广义的杨辉三角形［8］（亦称广义的Pascal三角形）由下列多项式的展开式系数构成：

广义的二项式系数满足下列等式：

k阶的Euler多项式［6,9］(x)由下列生成函数给出：

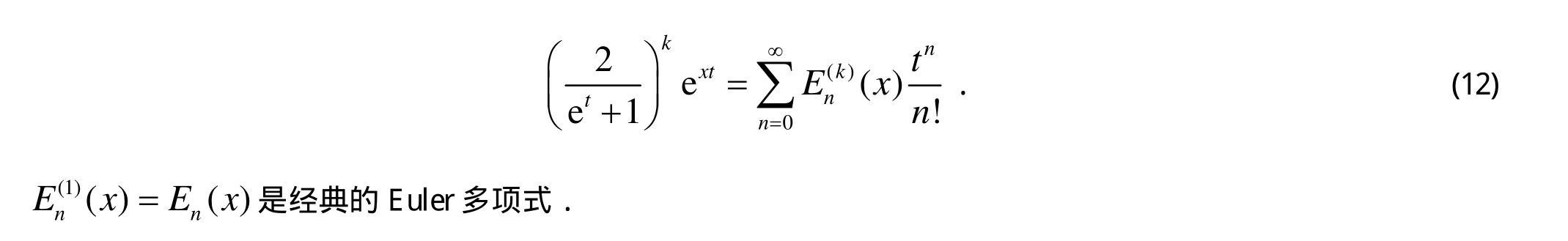
由式(12)可得

定理1令n∈ℕ,k∈ℤ，则

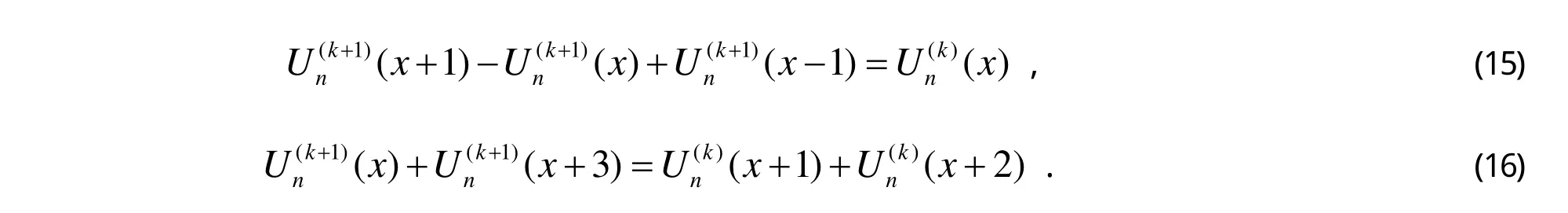
证明由式(6)可得

由式(17)、(18)得

定理2令n∈ℕ,k∈ℤ，则

证明应用数学归纳法来证明式(21)．当m=1时，式(21)显然成立．假设m≥2时式(21)成立，运用式(10)、式(11)和式(15)得

所以，对于自然数m+1，式(21)也成立．因此，由数学归纳法可知，对任意的自然数，式(21)都成立．证毕．

注2定理2中的 m = 1 ,2,3,有

定理3令n∈ℕ,k∈ℤ，则

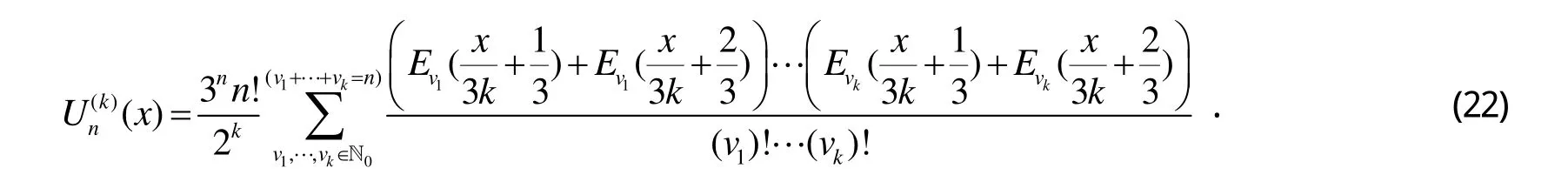
证明由式(6)、式(13)，可得

推论1令定理3中的k=1，则

注3显然,当式(24)中x=0时，即为结论式(5)．

定理4令n∈ℕ，则

证明由推论(1)和式(14)可得

推论2令定理4中的 x = 3 d , 3d + 1 ,3d + 2 ,d ∈ℕ,则

注4 令式(25)中的x=0或式(27)中的d=0，结论即为文献[1]中的定理2.5．

由式(6)容易得到：

由式(35) ~ (37)和中国剩余定理[10]可以推导出定理5．证毕．