绝热状态下板壳式换热器壳侧的流型与压降
2020-07-21吴鹏飞王科赵珏
吴鹏飞,王科,赵珏
(中国石油大学(北京)机械与储运工程学院,过程流体过滤与分离技术北京市重点实验室,北京102249)
引 言
热交换器是石油、化工、核能等工业应用领域中的主要设备之一,是合理利用与节约现有能源、开发新能源的关键设备,发展高效的热交换器能够有效地提高能源利用率,是解决能源问题与环境问题的重要途径。板壳式热交换器作为一种新型换热器[1-2],集合了管壳式换热器和板式换热器的优点,具有高的传热效率、能够耐高温高压、结构紧凑以及质量轻,并且弥补了板式换热器应力分布不均匀的缺点[3-4]。优良的性能使得板壳式换热器能够适用于多种复杂的工况,如压缩机级间冷却、浮式海上石油平台、有机朗肯循环发电装置等。
国内外学者针对板式换热器内流型和压降开展了广泛的研究。在单相流动形态中,Focke 等[5]、Dović等[6]、Zimmerer等[7]采用可视化的实验方法发现波纹通道内流动主要由两种形式组成:沿主流方向的纵向螺旋流动(Z 字形流动)和沿波纹方向的沟槽流动(L 字形流动)。栾志坚等[8]的研究表明随着波纹倾角由小变大,通道中的流动形态由“两组交叉流”转变成“曲折流”。众多研究者[9-16]的结果表明流型与波纹形状、波长、板间距、水力直径、流动方向有关。Nilpueng 等研究了不同相位角条件下的气液两相流流型[13],实验研究了垂直向上和垂直向下的两相流动形态,发现不同的流动方向也会导致流型的差异[14]。大部分研究者[10,12-16]大致将气-液两相流型划分为泡状流、弹状流、膜状流和搅拌流。在压降的研究中,有研究结果表明,表观气速和表观液速的变化对两相压降有显著影响,流动方向和流型也会影响两相压降,众多研究者[14-15,17-25]基于Lockhart-Martinelli 理论[26],并且得出相似的结论:在低水力直径的流道内Lockhart-Martinelli 关联式中的C值一般与管流中的气体层流-液体层流的C值较为接近。目前,对于板壳式换热器也有相应的研究,Abbas 等[27]对波纹角为45°和75°的板壳式换热器中的单相流进行了数值模拟,结果表明壳程的流动比板程的流动具有更高的Nu和更低的摩擦系数,此外,发现75°波纹角的传热性能优于45°波纹角。陈武滨等[28]的研究表明圆形截面形式的换热器壳程空间利用率较高,流体流动充分,换热效果更好。然而,对于板壳式换热器圆形波纹通道内气-液两相流型与压降的研究鲜有文献报道,其流道内的两相流相界面宏观结构和各相宏观分布的状态特征都与管内两相流的流动形态有较大差异,与传统的方形板式换热器的波纹通道也有不同,缺乏对板壳式换热器波纹通道内流动结构的多样性、流型转变机制及系统压力分布的认知。
本文主要对板壳式换热器圆形波纹通道内气-水两相垂直向上流动流型和压降进行了实验研究。获得了圆形波纹通道内气-水两相流动的宏观相界面分布特性,两相流动压降预测关联式以及两相流型与压降的相关性规律,丰富了对板壳式换热器的认识,具有十分重要的学术意义和科学价值。
1 实验装置及方法
1.1 实验装置
实验系统如图1所示,实验系统由储液罐、离心泵、空气压缩机、流量计、气液混合器以及相关的连接管段和多种阀门组成。实验测试段为前后两片透明波纹板片交错叠合构成菱形通道(图2),其材料为环氧树脂,尺寸参数列于表1,为保证实验段的充分发展以及进水和排水的均匀稳定,板片的进口和出口各设置150 mm的延长段。
1.2 测量方法与误差分析
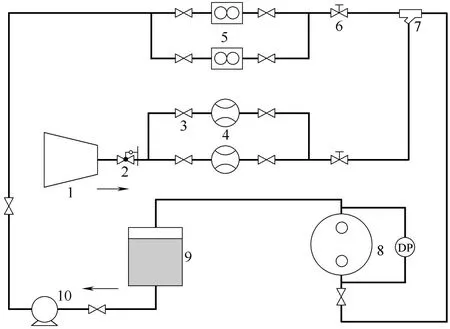
图1 实验系统Fig.1 Experimental system
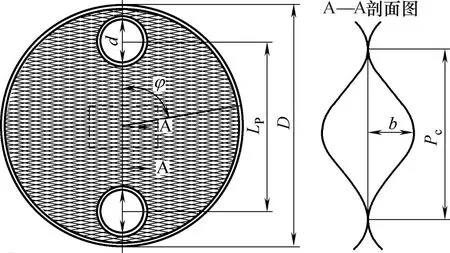
图2 板片几何结构Fig.2 Plate geometry
为了获得高清静态相界面特征以及捕捉流型转变特征,采用背光拍摄的方法。在实验结果的观察与流型识别过程中,根据光学原理,在透明波纹板片流道内气相与液相在光反射强度下的差异来区分液体连续相和气体连续相,可以清晰地观察到气相区域颜色是偏暗的,而液相区域视觉上则偏亮(图3),气-液相界面可以被明显区分,这一方法在流型识别中被广泛采用,图3 中的矩形区域表示图像拍摄区域,该区域是长为140 mm、宽为110 mm 的矩形。压力传感器分别布置在实验段的进出口,采样率为1000 Hz,时间为10 s,以获得压降变化规律;采用FR-625 高速摄影机和尼康60 mmf/2.8 微透镜进行流型捕捉以及流型转变的记录,采样频率和拍摄时间分别设置为500 帧/秒和5 s。实验过程中气体流量计的精度为±0.5%,液体流量计精度为±0.1%,压力传感器精度为±0.5%。

图3 拍摄区域与气液相的识别Fig.3 Shooting area and gas-liquid identification
2 结果与讨论
2.1 流型
根据两相流宏观相界面特征,将波纹通道内垂直向上流动的流型划分为泡状流、弹状流、膜状流和搅混流。

图4 泡状流(USL=0.025 m/s,USG=0.5 m/s)Fig.4 Bubbly flow(USL=0.025 m/s,USG=0.5 m/s)

表1 板片参数Table1 Plate parameters

图5 弹状流(USL=0.05 m/s,USG=1.5 m/s)Fig.5 Slug flow(USL=0.05 m/s,USG=1.5 m/s)
2.1.1 泡状流 如图4所示,在泡状流中,流道内液体为连续相,不同大小和形状各异的气泡分布在连续液相内,并与液体一起流动。流道内的气泡和液体的流动方向分为两种:一种是沿着菱形通道的间隙在竖直方向螺旋上升流动;另一种是沿着内外板片波纹方向的沟槽交替流动。在垂直向上流动中,由于重力作用极大地阻碍了竖直方向的螺旋上升流动,通过动态的图像显示,流动主要是沿着内外板片波纹方向的沟槽交替流动,如图4(a)所示沿着内板的沟槽方向流动,如图4(b)所示沿着外板的沟槽方向流动。
2.1.2 弹状流 随着气速的增加,流道内的气泡会合并成连续的气相,在接触点附近会出现液体滞留区,气速继续增加,整个流道内出现了连续的气相区域,接触点附近的液体滞留区变得更加明显,流型过渡至弹状流。如图5 所示,由于垂直向上流动受重力的阻碍作用,使得高速流动的气体将小液团从接触点位置带走的能力减弱,使得液体滞留区这一现象更加明显。由于流体之间的拖拽作用,使得接触点周围的小液团形状各异,并且显示出向上流动的趋势。
2.1.3 膜状流 随着气速的增加,流道内部分区域的液体滞留区会消失,部分会逐渐拉长成为细长的液团,气速继续增加,流道内的液体滞留区全部消失,在流道内形成连续的气相,液体在内外波纹板的壁面以液膜的形式随气芯快速流动,流型过渡至膜状流。如图6所示,膜状流中气体流量较大,液体流量较小,空气在中间流道流动,液体除了以液膜的形式在波纹板的壁面流动外,还有极少量液体以夹带液滴的形式存在于流道中。在垂直向上流动中,重力作用阻碍液膜沿着壁面向上流动,因此液膜的流动速度较小,厚度较厚。

图6 膜状流(USL=0.075 m/s,USG=5.0 m/s)Fig.6 Film flow(USL=0.075 m/s,USG=5.0 m/s)
2.1.4 搅混流 随着液体流量的增大,膜状流中的夹带液滴出现得更加频繁,导致液膜剧烈波动并且气体流通截面积减小,当膜状流界面上的剪切力远大于表面张力时,会形成液块并破坏膜状流中间的气芯,流型过渡至搅混流。如图7所示,一部分液体以液膜的形式沿着波纹板的壁面流动,剩余液体与气体在中间流道混合流动,在搅混流中,气液两相剧烈搅拌,很难区分出气液相界面,由于垂直向上流动会产生更剧烈的振荡,在波纹槽道内能看到很多小气泡。

图7 搅混流(USL=0.175 m/s,USG=5.0 m/s)Fig.7 Churn flow(USL=0.175 m/s,USG=5.0 m/s)
2.2 压降
2.2.1 单相压降 板壳式换热器中的单相压降包括摩擦压降、重力压降和压力损失。总压降表示为
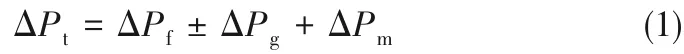
式中,ΔPt、ΔPf、ΔPg和ΔPm分别为总压降、摩擦压降、重力压降和压力损失。重力压降ΔPg通过式(2)计算

式中,g、L和ρl分别是重力加速度、流动长度和水的密度。
压力损失通过式(3)计算

式中,V表示水流速度。
Reynolds数Re表示为

式中,G表示质量流量,μ表示流体动力黏度,Dh表示水力直径。
单相摩擦因子的计算公式如下
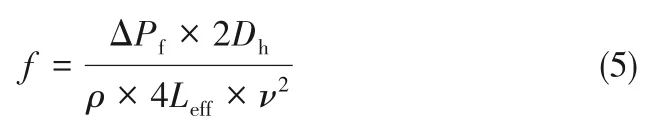
式中,Leff表示有效流动长度。
图8 显示了单相流动中空气和水的Reynolds 数与单相摩擦因子之间的关系,结果表明单相空气和水的摩擦因子都随着Reynolds 数的增加逐渐减小。实验结果与其他文献有着类似的趋势,如文献[27,29]等。数值的差异可以归因于不同的板片结构和板片的几何参数。基于实验结果,给出了单相空气和水的摩擦因子与Reynolds数的关联式。
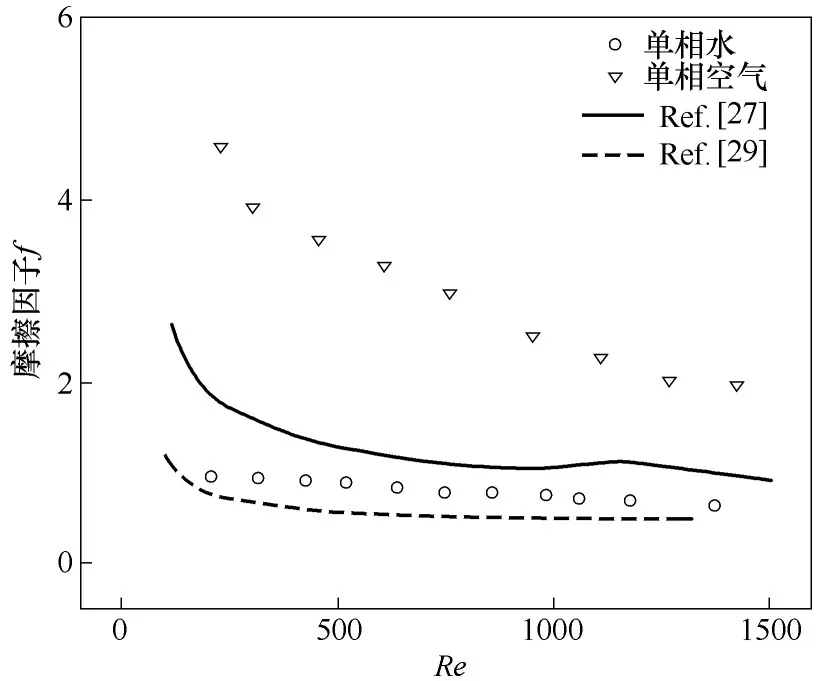
图8 单相流动中Reynolds数与摩擦因子的关系Fig.8 Relation between Re and friction factor in single-phase flow
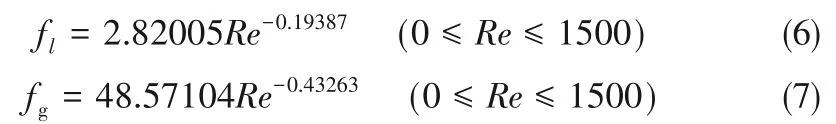
2.2.2 两相压降 图9 显示出了气-液两相摩擦压降与表观气速和表观液速的关系。结果表明,表观气速和表观液速都对两相摩擦压降有较大的影响,随着表观气速和表观液速的增大,垂直向上流动会导致流道内产生较强的振荡,湍流也变得更加剧烈,两相摩擦压降也增大。
本文采用均相流模型计算两相摩擦压降。两相流的混合密度由式(8)计算
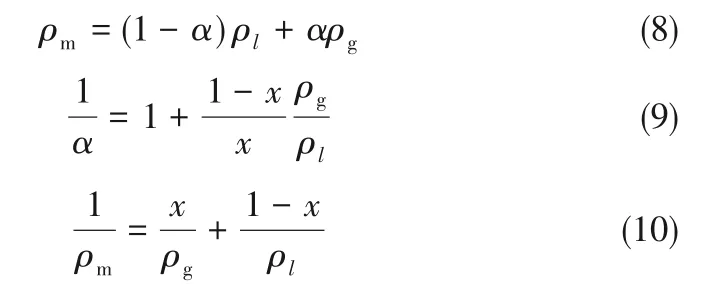
式中,ρm、ρl、ρg、α和x分别是气液两相的混合密度、液体密度、气体密度、含气率和气体干度。
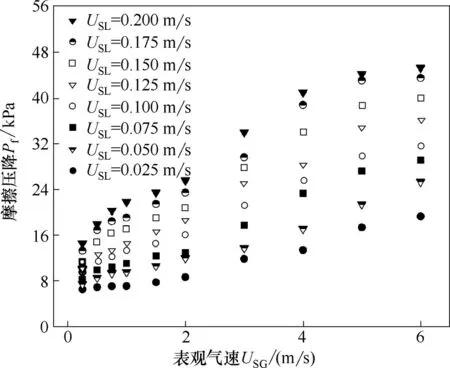
图9 两相摩擦压降与不同表观气速与表观液速的关系Fig.9 Relationship between two-phase friction pressure drop and superficial velocity
Lockhart-Martinelli 方法通常用于计算两相摩擦压降,计算式如下

式中,C值的大小取决于两种流体的不同流态。Chisholm[30]给出了光滑管内常数C的建议值,液体湍流-气流湍流,C=21;液体层流-气体湍流,C=12;液体湍流-气体层流,C=10;液体层流-气体层流,C=5。
两相摩阻系数(φL)与Martinelli 参数(X)之间的关系如图10所示。结果表明,随着Martinelli参数的增大,两相摩阻系数逐渐减小。基于实验结果,提出了一个新的关联式用于预测板壳式换热器波纹通道垂直向上流动的两相摩擦压降,如式(14)所示。大多数预测数据位于±30%偏差范围内。

图11 显示了实验结果与板式换热器流道中内两相摩阻系数与Martinelli 参数之间关系的比较。结果表明,板壳式换热器圆形波纹通道内两相摩阻系数(φL)与Martinelli 参数(X)的关系与板式换热器内具有较好的一致性。
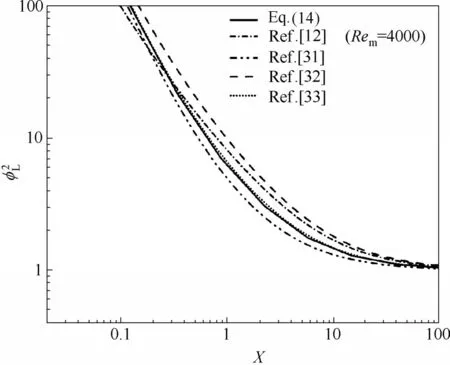
图11 两相摩阻系数与Martinelli参数的文献对比Fig.11 Comparison of relationship between two-phase multiplier and Martinelli parameter in literatures
2.3 两相流型与压降
图12 描述了板壳式换热器波纹流道内四种典型流型与其压降波动幅值的变化规律。结果表明:泡状流由于表观气速与表观液速较小,压降波动的幅度很小,基本维持在6.4~8.5 kPa 范围内波动;随着表观气速的增加,小气泡聚集合并形成弹状流,此时压降波动的幅度有所增加,基本在7.1~13.3 kPa范围内波动;随着表观气速的增加形成膜状流,膜状流流动较为稳定,压降波动幅度不大,压降基本在24.6~35.5 kPa 范围内波动;当液体流量增大时形成搅混流时,此时气-液两相在流道内扰动剧烈,在垂直向上流动伴随有较强的振荡,湍流增强,此时的压降波动幅度最大,基本在34.2~56.1 kPa 范围内波动。通过以上分析,可以看出不同的流型其压降的大小以及压降的波动幅度都有较大的差异,因此通过不同流型的压降波动幅度的变化可以为流型判别及其转变提供依据。
3 结 论
本文对板壳式换热器垂直向上流动的流型和压降进行了实验研究,主要结论如下。
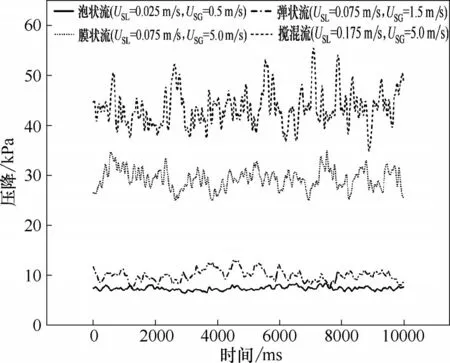
图12 流型压降波动曲线Fig.12 Fluctuation curves of flow pattern and pressure drop
(1)在本文波纹通道几何条件下,垂直向上气-液两相流动的流型被划分为泡状流、弹状流、膜状流和搅混流四种;此外,发现泡状流的流动是沿着内外波纹板的沟槽方向交替流动。
(2)在本文波纹通道几何条件下,基于Lockhart-Martinelli 理论获得了气-液两相流动的两相摩阻系数与Martinelli 参数的关系,并拟合了两相压降预测关联式,发现Chisholm 参数C的值与Chisholm最初建议的管内层流-层流的值接近。
(3)在本文波纹通道几何条件下,通过流型压降波动曲线得出泡状流中的压降波动幅值最小,弹状流与膜状流次之,搅混流中压降波动幅值最大,其压降波动的幅值可以为流型的种类判别及其转变提供一定的依据。
符 号 说 明
b——波纹深度,mm
D——板片直径,mm
Dh——水力直径,mm
d——角孔直径,mm
fl,fg——分别为液相摩擦因子和气相摩擦因子
G——质量流量,kg/(m2·s)
g——重力加速度,m/s2
L——总流动长度,m
Leff——有效流动长度,m
Pc——波纹节距,mm
ΔPf——摩擦压降,Pa
ΔPg——重力压降,Pa
ΔPm——压力损失,Pa
ΔPt——总压降,Pa
Re——Reynolds数
USG,USL——分别为表观气速和表观液速,m/s
V——流体速度,m/s
x——干度
α——含气率
μ——黏度,Pa·s
ρl,ρv,ρm——分别为液相密度、气相密度和气-液两相混合密度,kg/m3
ν——比体积,m3/kg
ϕL——两相摩阻系数
下角标
G——气相
L——液相
TP——气-液两相
