厚层堆积体偏压隧道洞口段动力响应特性研究

杜 斌, 张 熙， 刘大华， 陈 松, 陈先国

(1. 四川公路桥梁建设集团有限公司二分公司，四川成都 610066;2.西南交通大学交通隧道工程教育部重点实验室，四川成都 610031;3. 四川公路桥梁建设集团有限公司，四川成都 610200)

1 概述

随着我国高烈度地震区交通建设基础工程的发展，隧道结构以其良好的抗震性能而被广泛选择[1-2]。然而，近年来隧道工程震害事件频发[3]，从以往隧道震害情况来看，不良地质段特别是洞口及软硬岩交界面附近隧道结构破坏往往十分严重，这是因为一方面隧道洞口段围岩地质条件较差，多为强风化的堆积体，且与基岩地质条件差别较大，在地震发生时，山体容易产生滑动和坍塌掩埋隧道洞口。另一方面由于在软硬交界面附近，围岩性质变化不连续，在基覆交界面处隧道衬砌在剪切波和面波的作用下极易产生剪张性环向破裂[4]。因此研究隧道结构薄弱段的抗震设防设计是十分必要的。

目前国内外学者已经对高烈度地震区不良地质段的隧道结构动力响应展开了一系列研究，但针对洞口段覆有厚层堆积体偏压隧道的研究还不够深入。唐垠斐[5]研究了断层破碎带衬砌的地震动力响应规律及不同措施的抗减震机理及效果。江楠[6]结合隧道的宏观震害,分析了隧道的震害机理和震害影响因素,得到隧道结构的震害机理主要可以分为地震惯性力引起的破坏、地震强制位移引起的破坏和围岩失稳引起的破坏三类；造成隧道严重受损的因素大致包括地震参数、围岩条件、断层、隧道埋深、隧道自身条件等。禹海涛[7]推导任意动载作用下长大隧道纵向动力响应解析解,退化出行波效应下长大隧道纵向响应的理论解,直观地给出各参数之间相互关联的解析表达,并基于多质点-弹簧-梁模型进一步提出面向长大隧道纵向抗震设计的快速简化分析方法。欧尔峰[8]基于连续介质力学的离散元方法软件CDEM模拟水平岩层的结构面特性,主要针对不同水平岩层的厚度和不同地震动输入方向 ,分析了隧道衬砌关键部位的动力响应特性。

然而目前，针对厚层堆积体[9]的边坡稳定性研究较多，而对厚层堆积体覆盖下的隧道结构动力响应规律的研究很少,因此有必要深入地研究厚层堆积体隧道洞口段的动力响应特性。本文依托国道318线飞仙关隧道洞口段覆有厚层松散堆积体的工程实际,对洞口段穿越软硬交界面隧道动力响应特性进行深入研究。通过分析隧道衬砌结构的应力、变形和地震过程中的边仰坡塑性区变化，来讨论隧道抗震设防的关键位置。

2 依托工程概况

飞仙关隧道位于国道318线雅安至二郎山隧道段灾后恢复重建工程A1标段，全长1 608m，其中进口明洞为单压式明洞，长49m。进口段斜坡地表主要为稍密状块石土，斜坡坡度约为25～30 °，斜坡覆盖层厚约10m，表层未见变形迹象。围岩为残坡积块石土，以稍密状为主，厚度约10m，浅埋段易出现地表下沉过大或冒顶现象。具体构造部位处于龙门山断裂带西南段内，隧道主要围岩等级为Ⅲ、IV、V级，其中洞口段主要为IV级和V级。局部覆盖层及风化岩体松软，强风化岩体破碎，线状或淋雨状出水，大部分岩体较完整，点滴状出水。洞口段地质条件复杂，穿越了软硬岩交界面，且同时具有浅埋偏压的特点，强震作用下极易发生衬砌结构的破坏，因此研究该隧道洞口段的动力响应特性是十分必要的。

飞仙关隧道洞口结构横断面图如图1所示。隧道二次衬砌厚度为60cm，初支衬砌厚度为24cm，锚杆为φ25中空注浆锚杆，长350cm，间距为1.0m×1.0m(环×纵)。

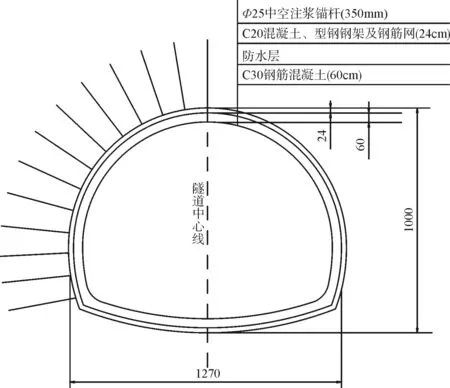
图1 飞仙关隧道结构断面(单位：cm)

3 隧道计算模型及力学参数

3.1 计算模型建立

本次计算以飞仙关隧道进口段为研究对象，隧道计算模型水平方向长度取120m，沿隧道纵向取60m，模型高度为85m，将软硬交界面倾角简化设为60 °。计算模型在X、Y、Z三个方向上的尺寸为120m×60m×85m，如图2所示。隧道围岩和二次衬砌采用实体单元模拟，初支衬砌采用壳单元模拟，其中围岩采用摩尔-库伦模型，二次衬砌则采用弹性本构模型计算。局部隧道结构和锚杆单元模型如图3所示。

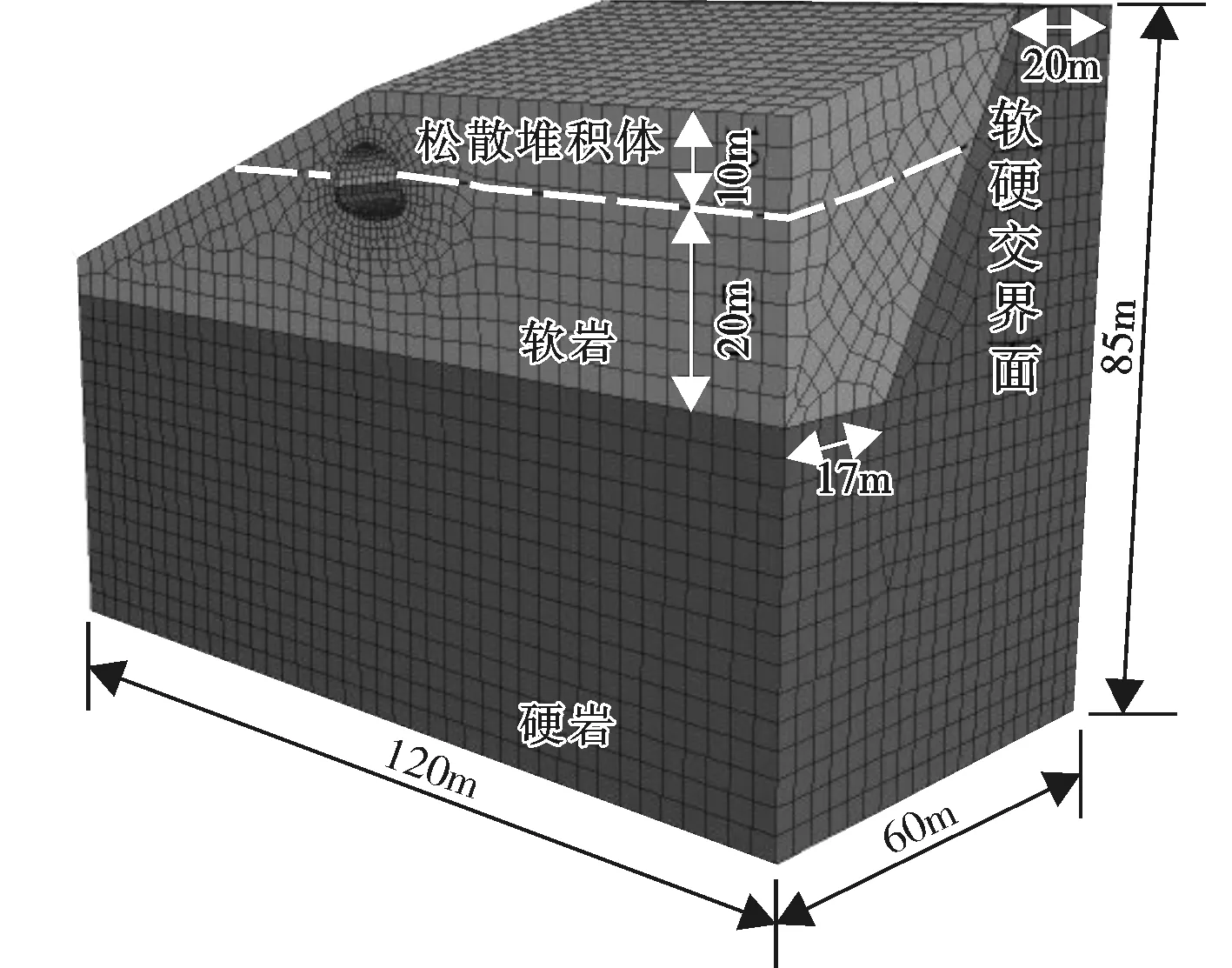
图2 隧道洞口整体计算模型

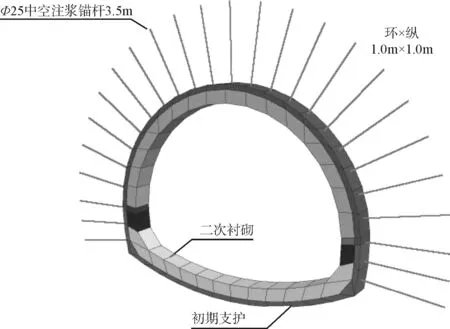
图3 隧道洞口整体计算模型

隧道洞口三维计算模型位置关系规定如下：

(1)X轴垂直隧道走向，以飞仙关隧道进口端隧洞口中线为x=0轴，左右各约60m。

(2)Y轴为隧洞走向方向，长度取60m。

(3)Z轴竖直向上，硬岩高度为45m，软岩高度为40m。

模型四周和底部采用法向固定约束，地表为自由表面。计算模型总共包含55 751多个单元和38 215多个节点，计算结果的精确度可以得到保证。

根据JTGD70-2004《公路隧道设计规范》和飞仙关隧道地质勘察资料并做相应调整，本次计算选取的围岩和隧道结构的物理力学参数如表1所示，锚杆物理力学参数如表2所示。

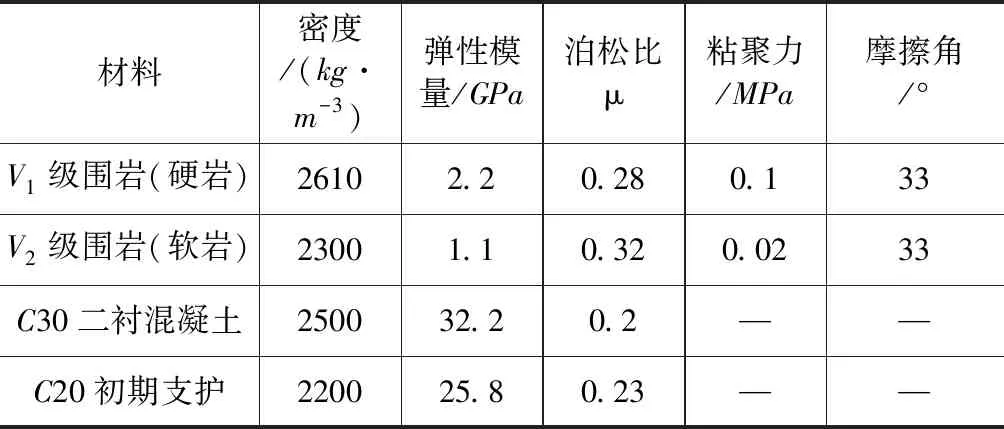
表1 隧道围岩与衬砌物理力学参数

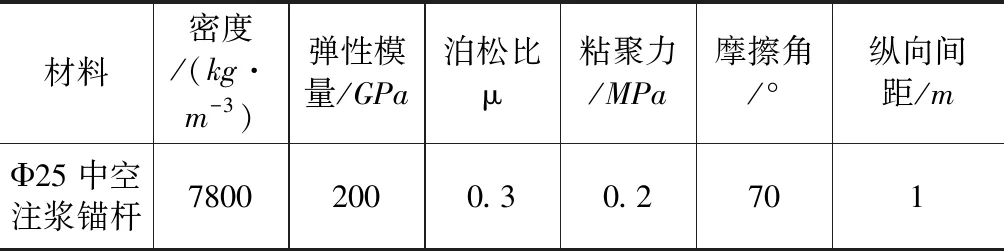
表2 锚杆物理力学参数

3.2 测点布置

在地震作用下，隧道结构随围岩同步震动，绝对位移很难反应隧道结构的变形和破坏情况，则相对位移相对更具有说服力。本文主要采取相对位移的分析方法，即同一断面地震动中相同时刻各质点的位移差值。在结构动力响应分析中主要参考指标为监测点的相对位移峰值。在本次数值模拟中，监测隧道断面对角线方向位移以及仰拱与拱顶之间的横向水平相对位移。故需在每个监测断面设置8个测点，4条测线。隧道断面的测点布置和横向位移如图4所示。

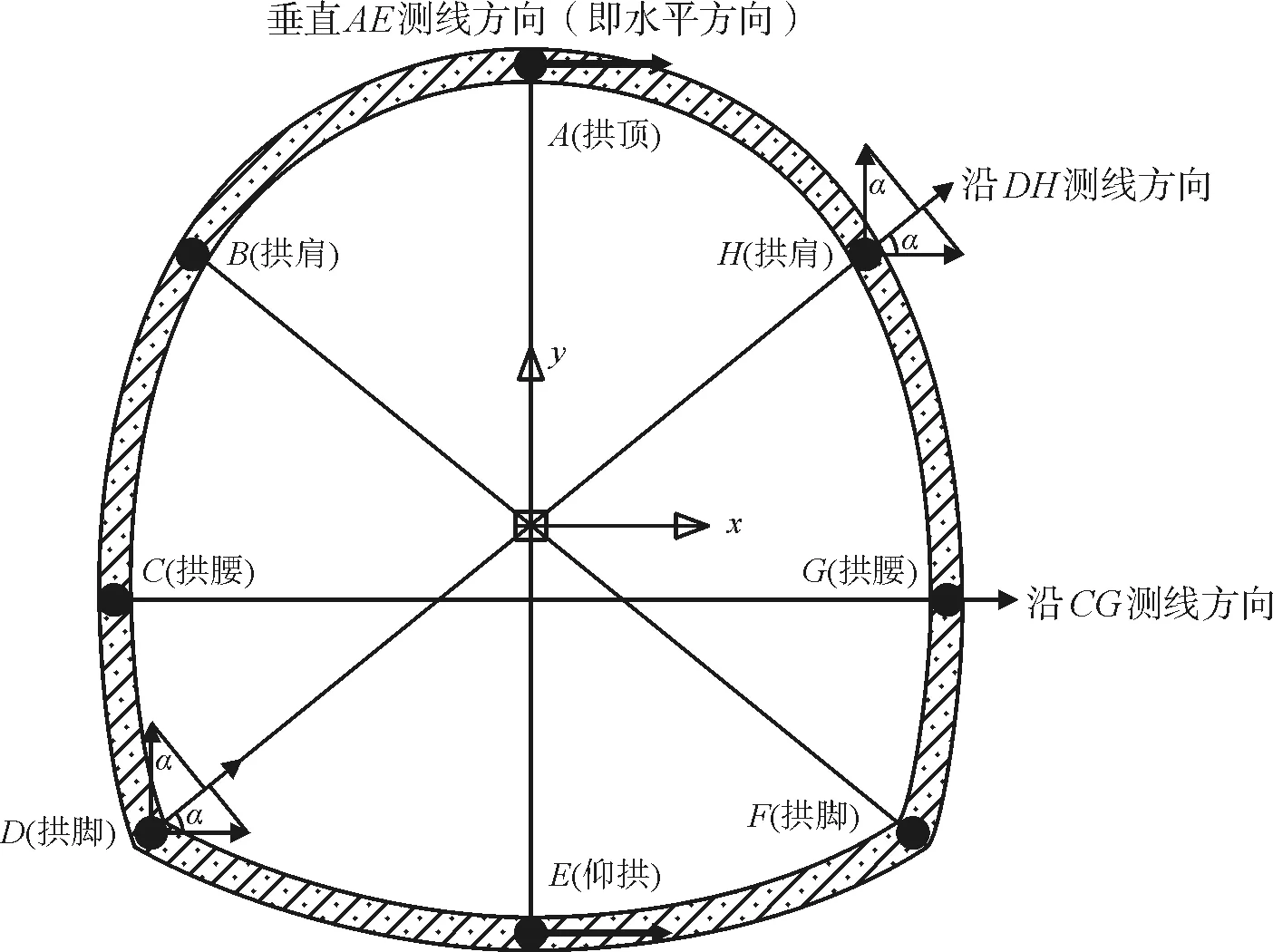
图4 隧道结构测线分布

D点沿DH测线方向的位移为：

ΔD=μDcosα+νDsinα

H点沿DH测线方向的位移为：

ΔH=μHcosα+νHsinα

式中：μ表示水平位移，ν表示竖向位移，其下标代表测点编号。

所以，D、H测点沿DH测线方向的相对位移为：

ΔDH=ΔH-ΔD

A、E测点沿垂直AE测线方向的水平相对位移为：

ΔAE=μA-μE

C、G测点沿CG测线方向的水平相对位移为：

ΔCG=μC-μG

在地震剪切作用下，隧道结构可能在纵向上产生相对错动，引发隧道轴向的弯曲变形等震害。为此，本文拟分析隧道关键测点的纵向相对位移。以拱顶位置垂直于AE测线方向(即水平方向)的纵向相对位移为例说明，如图5所示，A2点沿水平方向的纵向相对位移指的是A2点的水平位移减去A1点的水平位移。本文以软硬交界面处隧道横断面各个测点的位移为基准，其余断面处各个测点的纵向相对位移指的是该横断面与软硬交界面同一测点的相对位移(两点远离为正，靠近为负)。

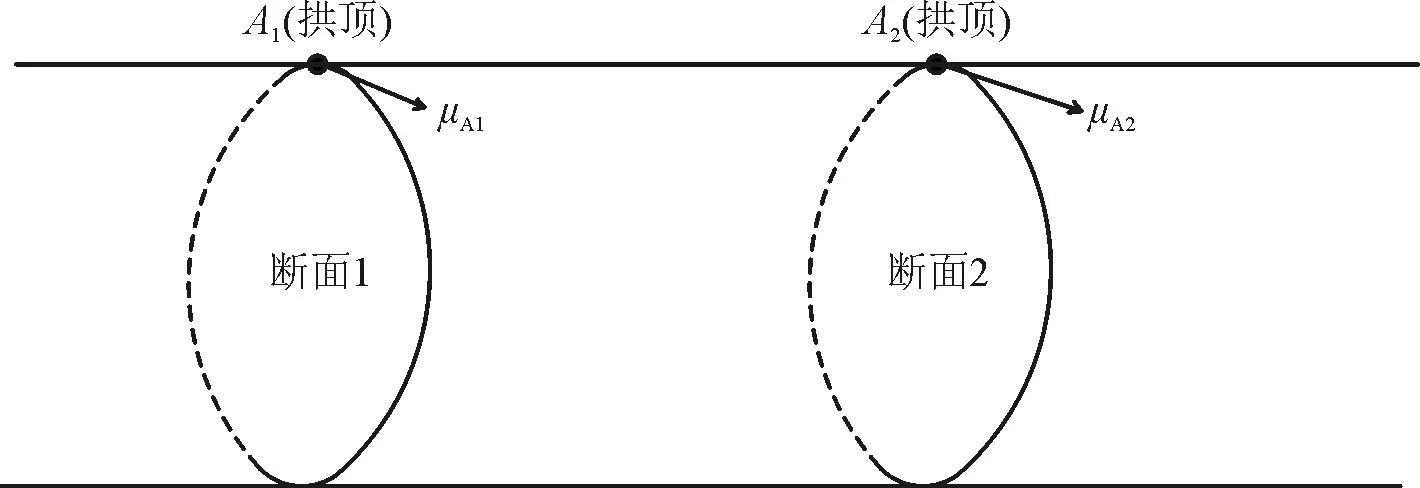
图5 测点纵向相对位移说明示意

隧道结构纵向监测断面布置如图6所示，在洞口段52m的区段内，每隔4m设置1个监测断面，共计14个断面，从监测断面编号进口方向依次编为1～14号。其中厚层堆积体及软岩段17m的范围内布置5个监测断面，在硬岩段26m的范围内布置7个监测断面，在软硬交界段附近12m布置2个监测断面。

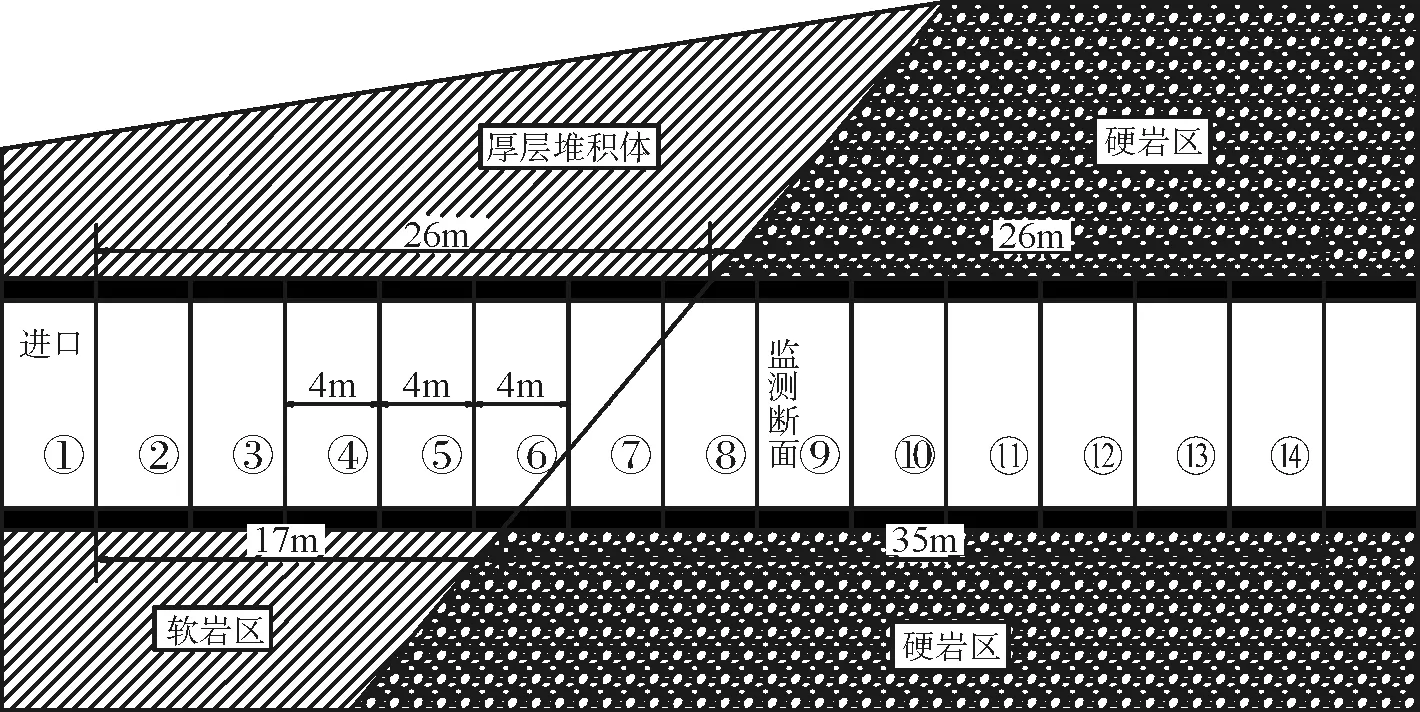
图6 隧道结构纵向监测断面分布

3.3 地震波输入

鉴于横向剪切波垂直于隧道轴向入射，将使隧道衬砌结构横断面发生拉伸和压缩破坏，是所有方向的地震波中破坏性最大的一种[10]，所以，本文采用垂直于隧道纵向的横向剪切波来模拟穿越洞口段隧道的动力响应。本文依托的飞仙关公路隧道工程区具体构造部位处于龙门山断裂带西南段内，且距卧龙镇较近，故选取汶川大地震卧龙波进行输入。原始卧龙波加速度时长约180s，加速度最大峰值发生在33.01s时刻，为957.7gal。考虑到动力计算耗时长的特点，对该地震波进行处理，选取振动最剧烈的的24～36s时间段作为地震动输入。由于地震波中绝大部分能量集中在0～18Hz的范围内，故本文采用SeismoSignal软件进行基线校正并过滤掉地震波中大于18Hz的成分。根据所测得的飞仙关隧道工程地震动峰值加速度为0.2g，在最终输入应力波时乘以0.2的系数进行折减，加速度时程曲线如图7所示。

4 计算结果分析

4.1 隧道结构变形

4.1.1 隧道结构横向变形

分别选取AE测线、DH测线、BF测线和CG测线在14个监测断面下的横向相对位移，提取14个监测断面的位移数据，4条测线的横向相对位移沿隧道纵向变化规律如图8所示。

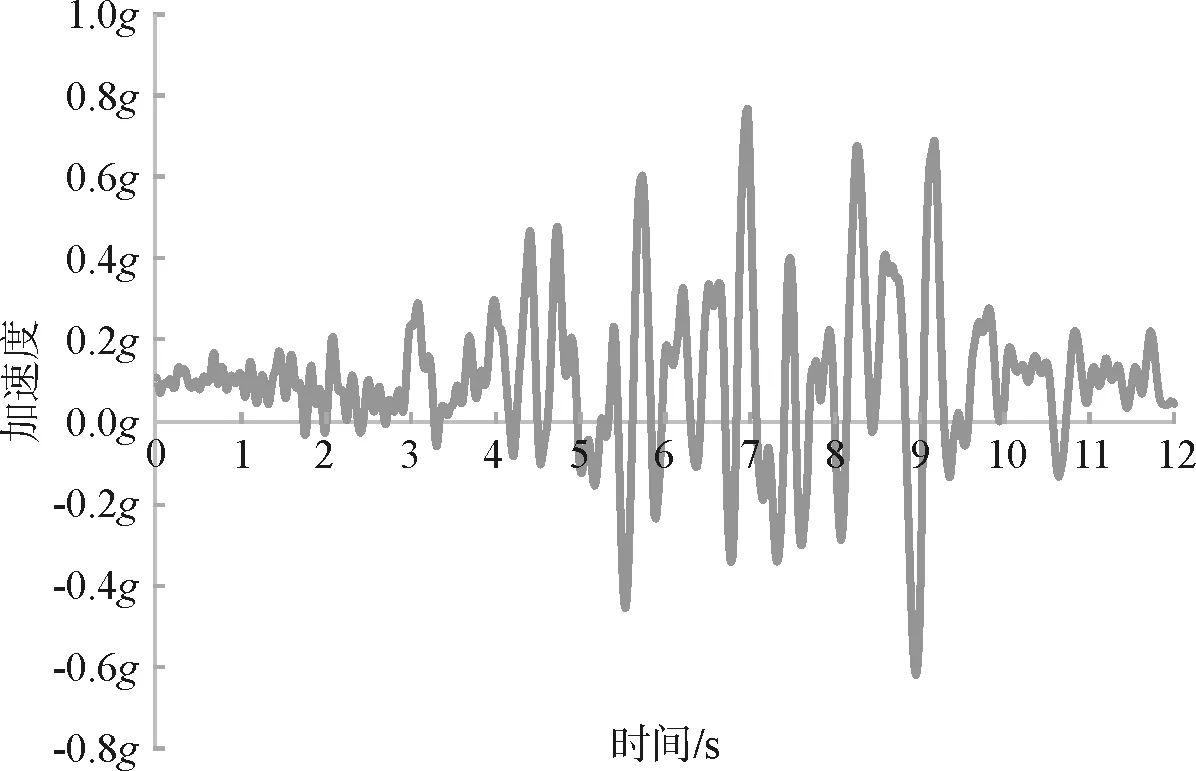
图7 地震加速度时程曲线

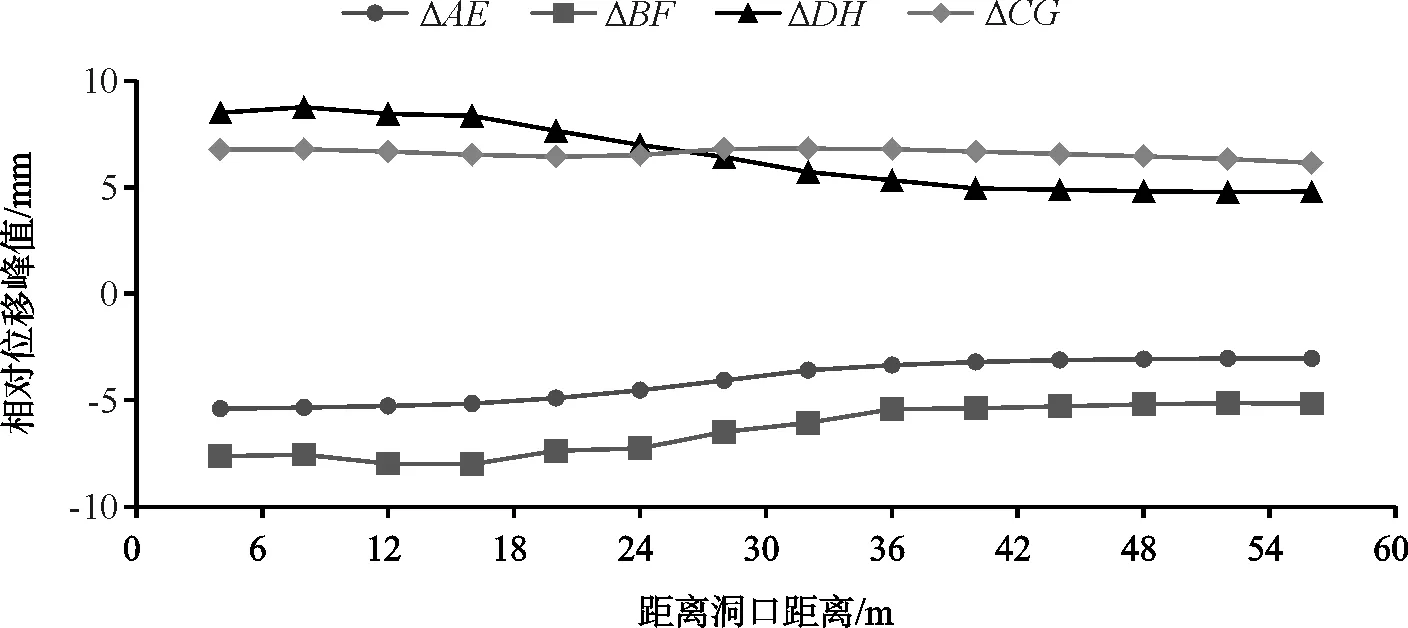
图8 隧道各条测线横向相对位移沿纵向变化

从图8可以看出，对于隧道上的各测线，在软岩区变化较明显，软硬交界面附近约6m的区间内相对位移有明显突变，硬岩段以后位移逐渐趋于平稳。DH测线数值不断减小，从最初洞口附近最大相对位移8.49mm减小至4.79mm，减少了43.6 %； AE测线和BF测线数值也不断减小，分别从最初的-5.40mm和-7.63mm减小至-3.04mm和-5.16mm，减小了43.7 %和32.4 %。CG测线整体变化较为平缓，始终维持在6.55mm附近。

4.1.2 隧道结构纵向变形

本节对隧道衬砌较有代表性的拱顶、仰拱、左供腰和右拱腰四个位置的纵向相对位移峰值沿隧道轴向的变化规律进行分析，见图9。

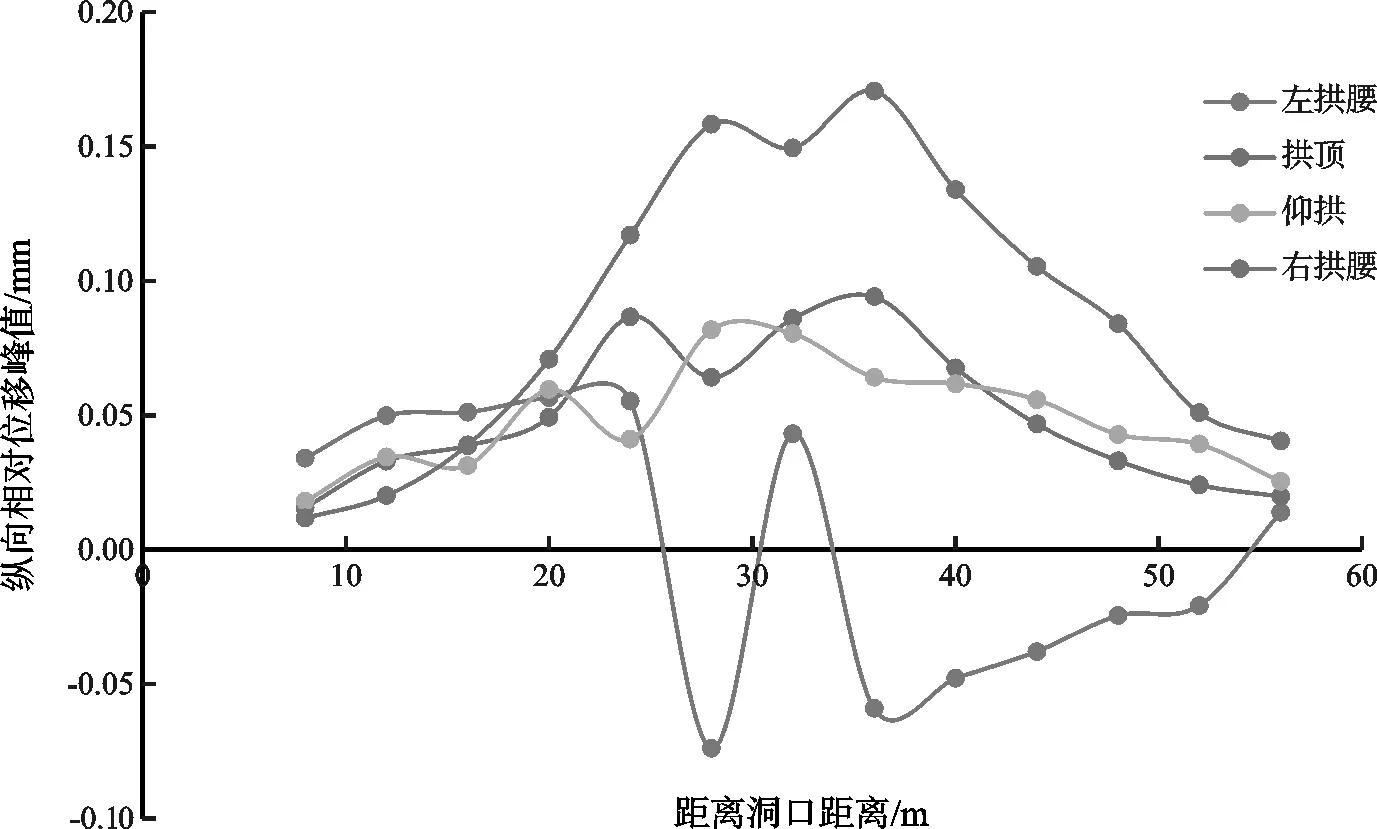
图9 隧道各位置纵向相对位移变化

从图9可以看出，拱顶、仰拱和右拱腰纵向相对位移均为正，左拱腰纵向相对位移有正有负。在软岩段，随着开挖的进行，围岩变形不断增大，导致各条测线的纵向相对位移呈增大的趋势。在软硬交界面附近时，纵向相对位移呈波动状。在硬岩段，四条测线纵向相对位移均减小。从整体上看，右拱腰的纵向相对位移变化幅度最大：从起始的最小值0.012mm至软硬交界面附近的最大值0.171mm。拱顶和仰拱变化幅度不大，且两者位移值较为接近。左拱腰的纵向相对位移变化很大，且在软硬岩交界面附近正负波动，峰值达到了0.055mm和-0.074mm。总体来看，隧道纵向相对位移在Y=20～50m区间范围内变化最大，可见隧道在穿越软硬交界面段的纵向相对变形相对较大，说明在隧道纵向上的同一位置的位移基本同步变化的，呈整体变形。

4.2 隧道结构受力

根据第三强度理论所述，材料的破坏强度是由最大剪应力所决定的。最大剪应力的公式为：

τmax=0.5(σ1-σ3)

式中σ1、σ3分别为最大主应力和最小主应力。

第三强度理论的等效应力公式为：

σs=σ1-σ3

所以，在本文中所分析的应力均为第三强度理论的等效应力σs。

4.2.1 隧道结构纵向受力分析

沿纵向提取隧道关键点的应力在地震中的峰值，以判断地震作用下衬砌结构沿隧道轴向的受力状态，如图10所示。

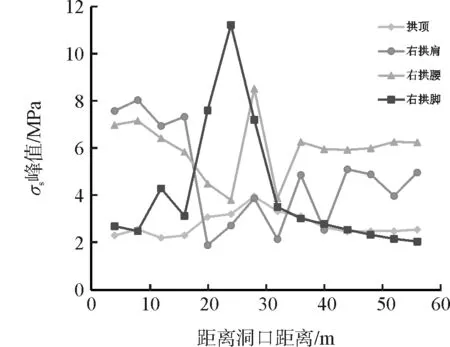
(a)拱顶及右拱肩、 腰、脚应力峰值

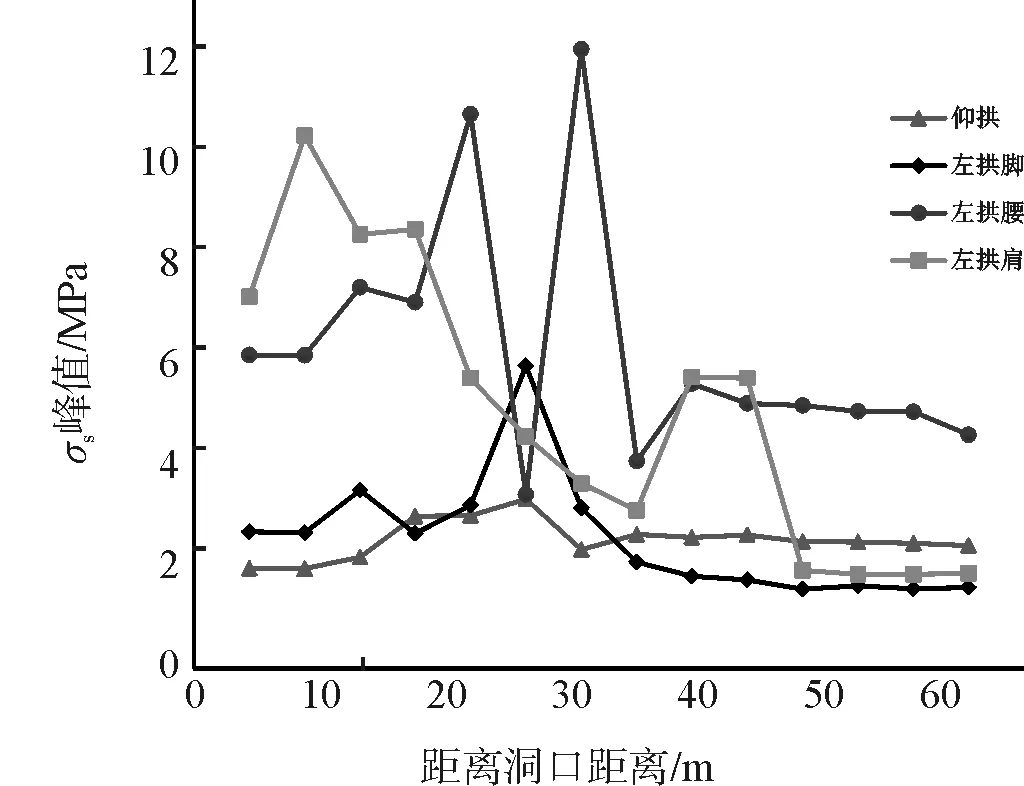
(b) 拱顶及左拱肩、 腰、脚应力峰值

从图10可以看出，隧道各测点应力峰值在软岩段至软硬交界面段的起伏较大，而在硬岩段的起伏较为平稳。在软岩段，拱肩和拱腰位置的应力远远大于其他位置的应力，其中应力较大的位置发生在Y=10～17m区间的右拱肩、左拱肩和右拱腰位置，应力峰值分别为8.04MPa、7.97MPa和7.16MPa。在软硬交界面附近区间(Y=21～36m)内，除仰拱和拱顶位置外，其余位置的应力变化范围十分大：左、右拱腰位置应力呈波动状，峰值最大值分别为9.26MPa和8.53MPa，峰值最小值分别为2.60MPa和3.81MPa；左、右拱脚位置应力达到最大值，分别为4.53MPa和11.23MPa；左、右拱肩位置应力达到最小值，分别为2.37MPa和1.90MPa。在硬岩段(Y=37～56m范围内)，除左、右拱肩外，其余位置的应力变化较为平缓。

4.2.2 隧道结构横向受力分析

本节分别在软岩段、软硬交界面附近、硬岩段取三个横断面，进行应力分析。隧道衬砌横向受力如图11～图13所示。

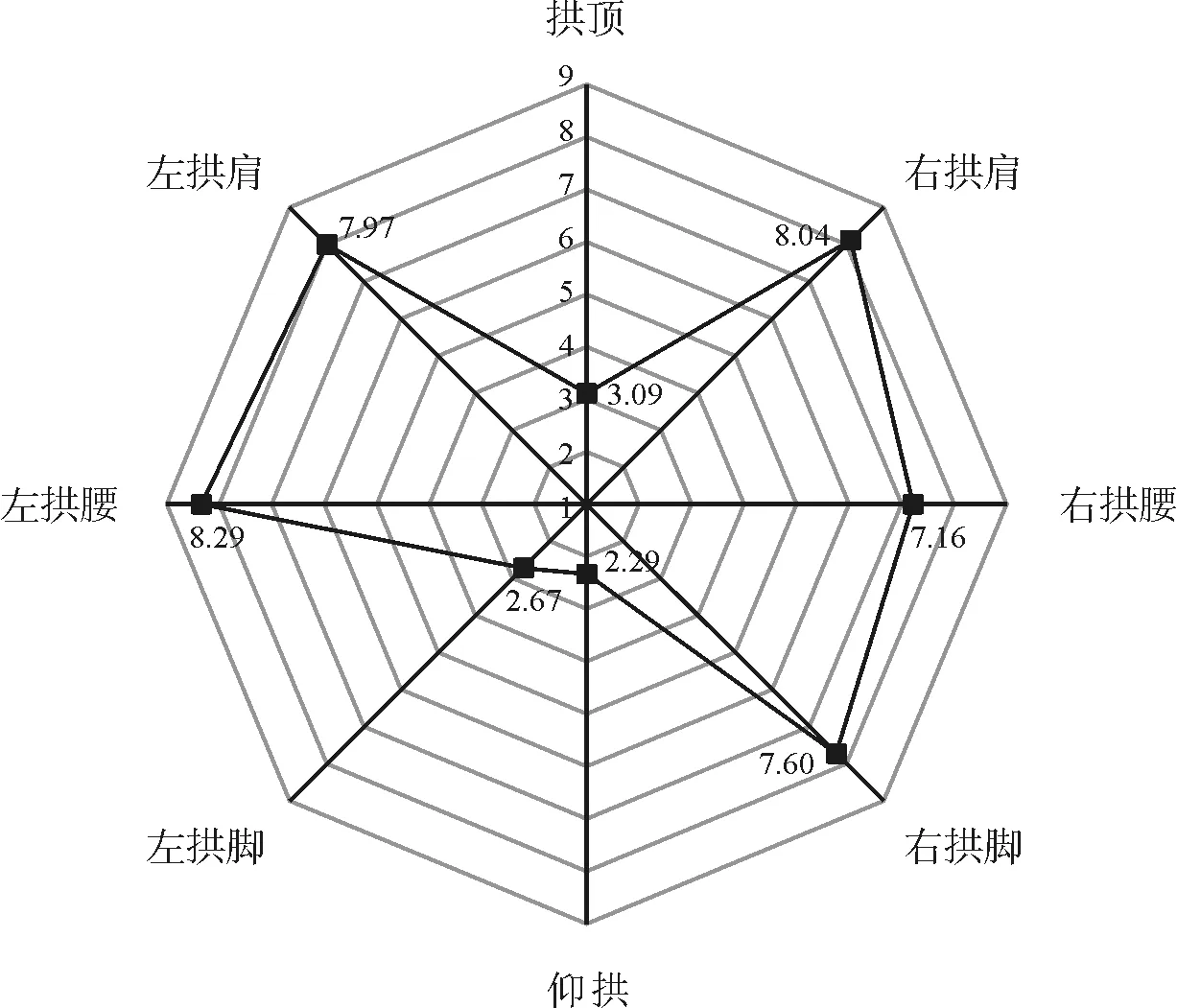
图11 隧道软岩段衬砌横向受力(单位：MPa)

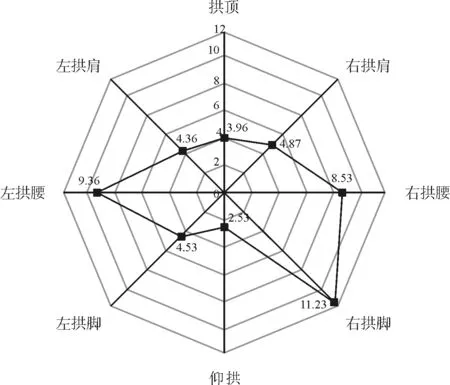
图12 隧道软硬交界面处衬砌横向受力(单位：MPa)

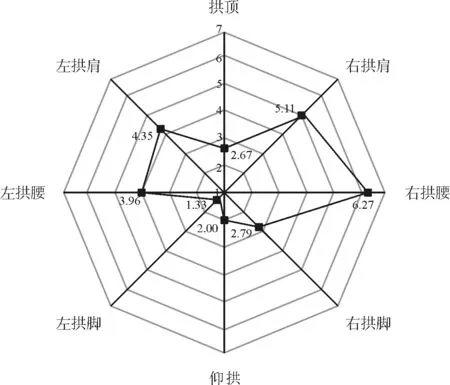
图13 隧道硬岩段衬砌横向受力(单位：MPa)

由图11～图13可知，软岩段左右拱肩及拱腰处应力峰值最大，约为8MPa左右，右拱脚处应力值也较大，拱顶、仰拱和左拱脚处的应力峰值较小，约为2.5MPa。软硬交界段右拱脚应力峰值最大，为11.23MPa，其次是左右拱腰，约为9MPa，其余位置的应力峰值较小。在硬岩段右拱腰处应力峰值最大，为6.27MPa，其次为左右拱肩及左拱腰，应力峰值约为4MPa，其余位置应力均较小。因而对衬砌设计时，应尤其关注拱腰和拱脚位置，进行适当加强。

4.3 洞口边仰坡塑性区分析

本节主要分析模拟地震过程中第6s和地震结束时的12s时刻飞仙关隧道洞口边仰坡塑性区破坏范围和程度，如图14、图15所示。

图14 地震时隧道洞口边仰坡塑性区分布云图(6s时刻)

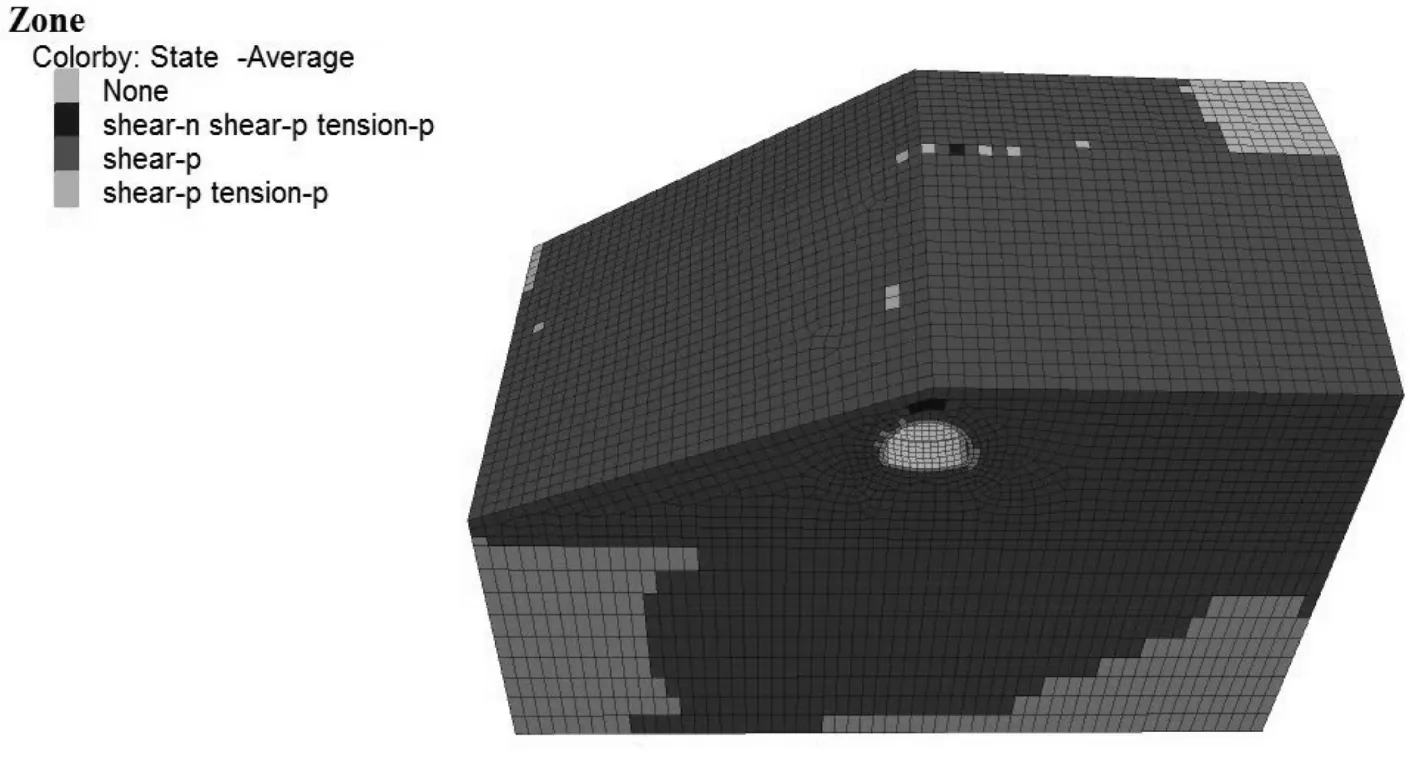
图15 地震时隧道洞口边仰坡塑性区分布云图(12s时刻)

图14、图15可以看出，在地震动6s时刻，边仰坡上就出现了较大的塑性区，只有边坡中部和下部以及仰坡的上部大部分位置还未受塑性破坏，塑性区体积约为313 141m3。地震后(12s时)整个洞口边仰坡范围内几乎全受过塑性破坏，只有仰坡后方一小片区域还未受到破坏，塑性区体积约为428 839m3。

5 结论

本文分析了强震作用下山岭隧道结构地震动力响应基本原理，通过有限差分软件建立数值模型，模拟在地震作用下穿越软硬交界面隧道结构的动力响应特性。通过分析地震动过程中隧道衬砌结构的应力、变形和围岩塑性区的破坏程度及范围，得出了以下结论：

(1)由于数值模型中地震波垂直向上输入，衬砌收到较大的水平剪切力作用，导致隧道衬砌的横向变形明显大于纵向变形。并且横向相对位移在软岩区和软硬交界面附近变化较明显，硬岩段以后位移逐渐趋于平稳。纵向相对位移数值较小，说明衬砌在地震波作用下沿隧道轴向不易发生变形，主要破坏形式为水平横向剪切破坏。

(2)通过比较8个测点在14个监测断面下的应力峰值，可看出右拱脚、左拱肩和左拱腰位置等应力峰值在软硬交界面出现极值点，且应力变化十分迅速，可见这三个点为地震动下为隧道结构的危险位置，应着重加强抗震设防。

(3)随着地震波的输入，洞口上方的边仰坡塑性区破坏范围迅速增大，在地震动中6s时刻和地震动结束的12s时刻，边仰坡塑性区体积增加十分迅速。可见在洞口段的边仰坡应适当加强防护，以减少地震动后边仰坡的滑坡、垮塌。