面内受压大跨度混凝土板自由振动
2020-07-21刘露,谢智
刘 露, 谢 智
(1.中交二航局成都城市建设工程有限公司, 四川成都 610041; 2. 中交第三航务工程局有限公司厦门分公司, 福建厦门 361000)
基于现代结构理论和城市建设的发展,大跨度混凝土结构具有构件截面小,自重弯矩占总弯矩的比例小,优越的跨越能力等重要特性,从而使大跨度混凝土板在新建的市政项目应用普遍。范康等[1]基于板壳振动理论,根据楼板振动舒适度的要求、边界条件、楼板跨度等因素对大跨度混凝土板的振动特性进行了研究。李冬等[2]借鉴欧洲EFNARC标准,利用四边简支方板试验研究了钢纤维对玄武岩纤维编织网增强混凝土板双向弯曲性能的影响。王丽娟等[3]对水泥混凝土路面固化温度区域特征及其对面板翘曲的影响进行了研究。李炎隆等[4]利用平面有限元法分析坝踵混凝土体型对混凝土面板应力变形的影响。韩重庆等[5]为分析不同持荷水平下受约束预应力混凝土空心板整浇楼面的耐火极限变化规律,进行了3块受约束预应力混凝土空心板整浇楼面试件的耐火极限试验研究。王园园等[6]对钢-混凝土组合与叠合双重作用梁负弯矩区刚度和叠合面滑移进行了研究。黄春霞等[7]研究单掺纤维和混掺纤维对活性粉末混凝土抗压强度和轴向抗拉强度的影响规律。董毓利等[8]对火灾作用下混凝土双向简支板的挠度进行了计算。
混凝土板作为最基础的建筑构件在市政工程中应用极为广泛,如用于路面承重结构、桥梁、楼板,地铁车站等。同时由于功能和结构的需要,大跨度混凝土板也常见于市政工程中,深入分析其在面内荷载等多种载荷作用下的力学响应具有理论研究意义和工程实际应用价值。目前,面内受压大跨度混凝土板自由振动和屈曲的分析在国内外还鲜见有文献报道,因此本文研究面内受压大跨度混凝土板自由振动和屈曲问题。首先基于经典薄板理论,利用Hamilton原理推导面内受压大跨度混凝土板自由振动和屈曲的控制微分方程并进行无量纲化;其次采用微分变换法(DifferentialTransformMethod, 简称DTM)将问题的无量纲控制微分方程及其边界条件进行变换;最后求解并探讨了无量纲压力强度、载荷参数和长宽比对于混凝土板自振频率的影响。
1 控制微分方程及参数的无量纲化
考虑如图1所示的大跨度混凝土板,将其放置在图示的笛卡尔直角坐标系中。板的尺寸为a×b×h且受到垂直于y轴截面上的面内分布力Ny=-N0(1-γx/a),其中N0为x=0处的压力强度,γ为载荷参数。这里用λ=a/b表示矩形板的长宽比,垂直于板面的位移分量为w。y=0和y=b处为简支边界(S),其余对边为简支(S)或夹紧(C)边界。下面在对纳米矩形板四个直边的边界条件表示中,均按x=0、y=b、x=a和y=0处的次序给出。
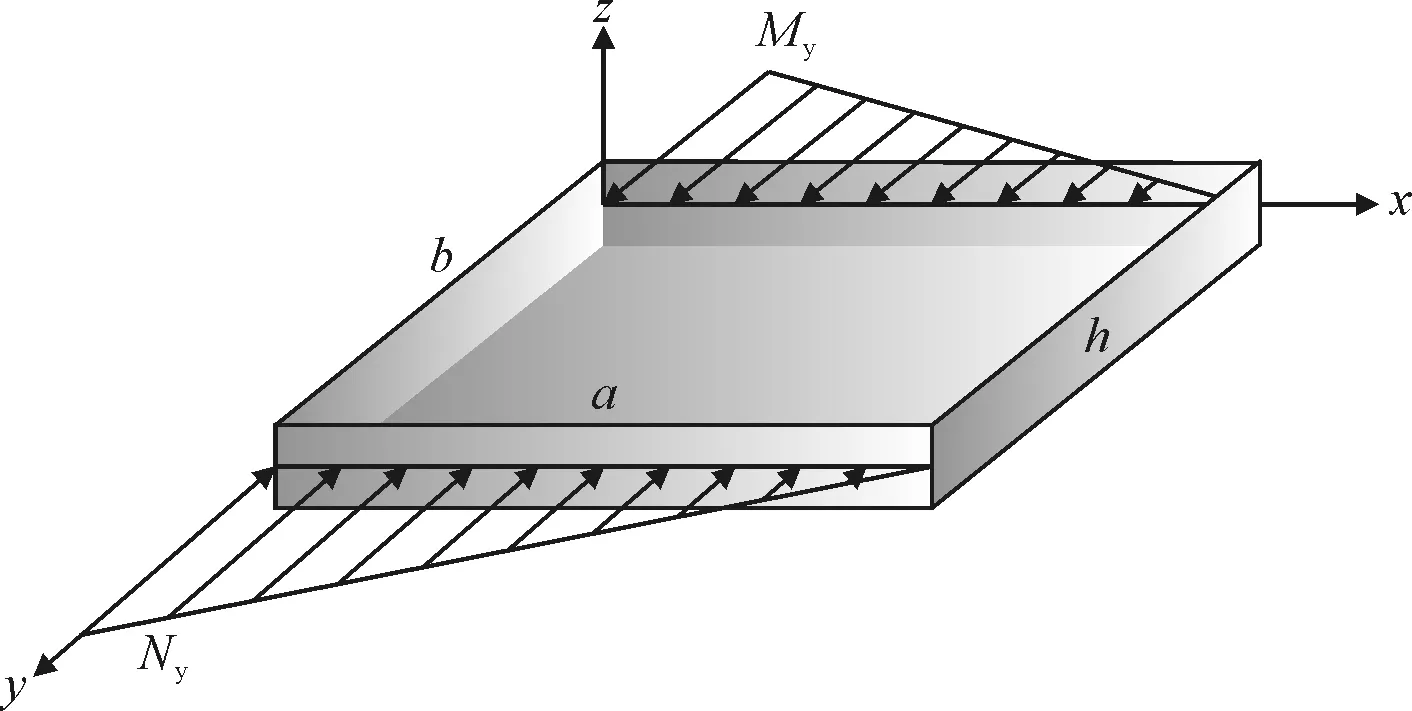
图1 面内受压大跨度混凝土板
为了导出大跨度混凝土板自由振动控制微分方程,运用Hamiltion原理表示如下:
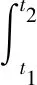
(1)
式中:t表示时间,δ为变分符号。U、T和W分别表示板的应变能、动能和外力势能,各量可表示如下:
(2)
(3)
(4)
式中:σx、σy和τxy为三个应力分量,εx、εy和γxy为三个应变分量,ρ为质量密度。
板中面应变和内力分量如下[9]:
(5)
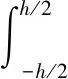
(6)
将式(2)~式(6)代入式(1)可得面内受压大跨度混凝土板的运动方程为:
(7)
在二维形式的板应力应变关系如下:
(8a)
(8b)
σxy=Gγxy
(8c)
式中:E、G=E/2(1+ν)分别为正交各向同性材料的两个弹性模量;v为泊松比。
由式(5)、式(6)和式(8)可得混凝土板的弯矩和扭矩方程:
(9a)
(9b)
(9c)
式中:D=Eh3/[12(1-ν2)]为弯曲刚度。
式(9a)~式(9c)代入式(7)可得面内受压大跨度混凝土板的运动方程为:
(10)
板的边界条件在y=0和y=b处若只考虑为简支(S),板的横向位移函数可取为:
(11)
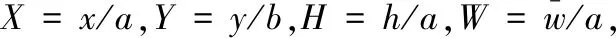
Ω2=[12ρ(1-ν2)a2ω2]/EH2,
N0*=[12N0(1-ν2)]/aEH3,
并由式(10)、式(11)可得面内受压大跨度混凝土板自由振动的控制微分方程为:
(12)
式中:
A1=1,
A2=-2λ2m2π2
A3=γλ2m2π2N0*,
A4=λ4m4π4-λ2m2π2N0*-Ω2
又由弹性稳定性理论可知,结构失稳时的振动具有无限大的振动周期,其固有频率为零[10],则式(14)中若取Ω=0,则可得到计算面内受压大跨度混凝土板各阶屈曲模态载荷的控制微分方程,其最小值即屈曲临界载荷。至于在X=0和X=1边界处,可为简支(S)边界条件或者固定(C)边界条件,其无量纲形式表述如下:
简支(S):
(13)
固定(C):
(14)
2 无量纲控制微分方程及其边界条件的DTM变换
面内受压大跨度混凝土板自由振动和屈曲的无量纲控制微分方程式(12)为变系数常微分方程,一般情况下较难求得其解析解,这里采用微分变换法(DTM)[11-14]进行求解。DTM是一种能有效将线性或非线性微分方程(组)变换成代数方程(组)求解的半解析方法,它基于Taylor级数展开来求解微分方程,使用充分可微的多项式形式作为精确解的近似。经DTM变换,可将原微分方程(组)和系统边界条件转化为由离散函数构成的代数方程(组),非常适合计算机编程进行求解。对于原函数f(x),根据函数的Taylor公式,经过DTM变换后的函数F[k]定义为[20]:
(15)
F(k)的逆变换为:
(16)
或者:
(17)
在实际应用中,函数f(x)只考虑级数的有限项,式(14)可重写为:
(18)
式中:正整数m表示Taylor级数的项数。通常情况下可通过增大m的值来提高解的精度。
运用DTM对面内受压大跨度混凝土板自由振动和屈曲问题进行求解时,首先需要将其无量纲控制微分方程和边界条件经DTM转化为相应的由离散函数组成的代数方程。这里用F表示式(12)中W经DTM变换后的离散值,则式(12)由DTM可变换为:
B1F[k+4]+B2F[k+2]+B3F[k]+B4F[k-1]=0
(19)
式中:
B1=(k+1)(k+2)(k+3)(k+4),
B2=-2λ2m2π2(k+1)(k+2),
B3=λ4m4π4-Ω2-λ2m2π2N0*
B4=γλ2m2π2N0*
边界条件变换如下:
在X=0处,简支(S)边界条件:
F[0]=F[2]=0
(20)
固定(C)边界条件:
F[0]=F[1]=0
(21)
在X=1处,简支(S)边界条件:
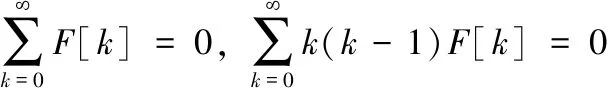
(22)
固定(C)边界条件:
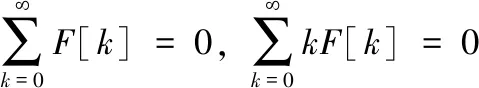
(23)
将式(19)分别代入式(20)和式(22),式(20)和式(23),可分别求得四边简支(SSSS)和三边简支一边固定(SSCS)的频率特征方程如下:
S11(n)(Ω)F[1]+S12(n)(Ω)F[3]=0
S21(n)(Ω)F[1]+S22(n)(Ω)F[3]=0
(24)
式中S11(n),S12(n),S21(n),S22(n)是迭代n次求出的含有未知量无量纲固有频率Ω的多项式,写成矩阵的形式:
(25)
要使式(25)有非零解,则:
(26)
令无量纲固有频率Ω=0,给定参数可以求解出临界屈曲载荷Ncr。Ncr的求解过程类似于Ω的求解过程,同理可得:
(27)
在对边简支对边固定(CSCS)、一边固定三边简支(CSSS)的边界条件下,同理可求出含有未知量无量纲固有频率Ω以及临界屈曲载荷Ncr特征方程:
(28)
(29)
由式(26)~式(29),SSSS、SSCS、CSCS、CSSS边界条件下的无量纲固有频率Ω和临界屈曲载荷Ncr可求出。为了控制求出的无量纲固有频率Ω和临界屈曲载荷Ncr的精度和研究其收敛性,则有:
|Ωj(n)-Ωj(n-1)|≤η1, |Ncrj(n)-Ncrj(n-1)|≤η2
(30)
式中:η1、η2为迭代误差限,这里取η1=η2=0.000001。
3 计算结果与分析
通过编写MATLAB程序可获得由DTM求解面内受压大跨度混凝土板屈曲和振动特征值问题的临界载荷Ncr和无量纲频率Ω。这里选择C35混凝土进行计算。材料参数如下[1][24]:ν=0.2,E=3.15×104N/mm2,ρ=25kN/m2。
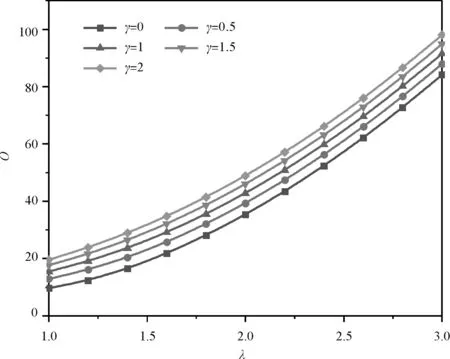
图2为N0*=30,m=1,H=0.1时,在CSCS、CSSS、SSCS、SSSS边界下1阶无量纲固有频率Ω与载荷参数γ的关系曲线。各边界下的Ω都随γ的增大而增大;约束较强边界下Ω较大(顺序:CSCS边界下频率值>CSSS边界下频率值或SSCS边界下频率值>SSSS边界下频率值)。
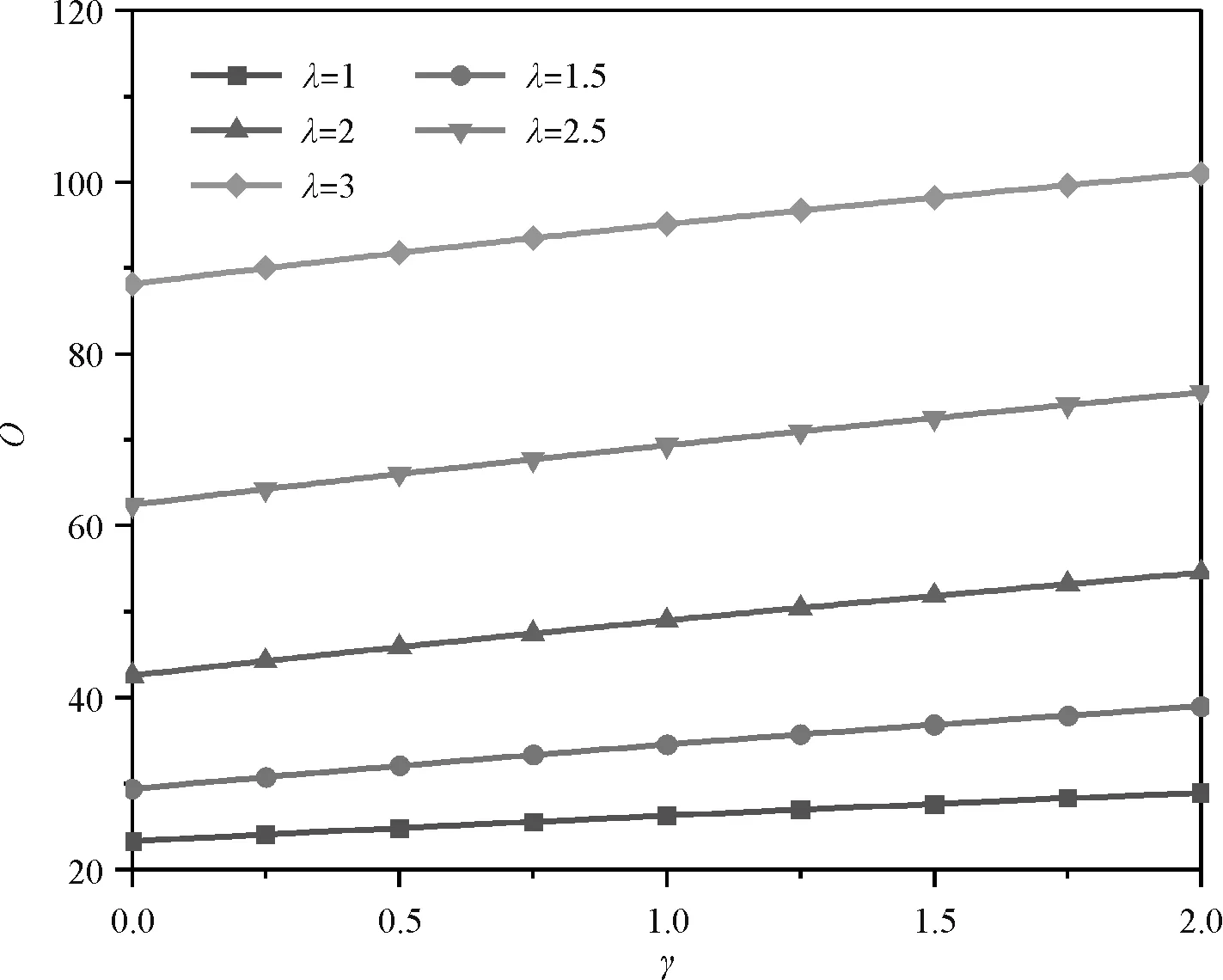
(a)CSCS边界条件
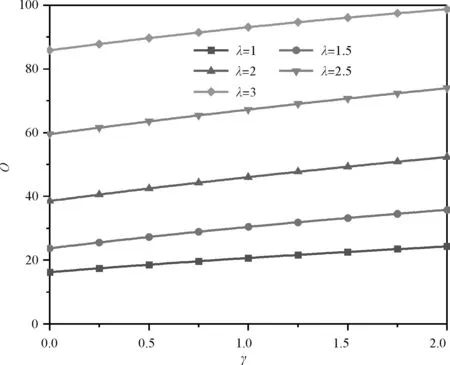
(b)CSSS边界条件
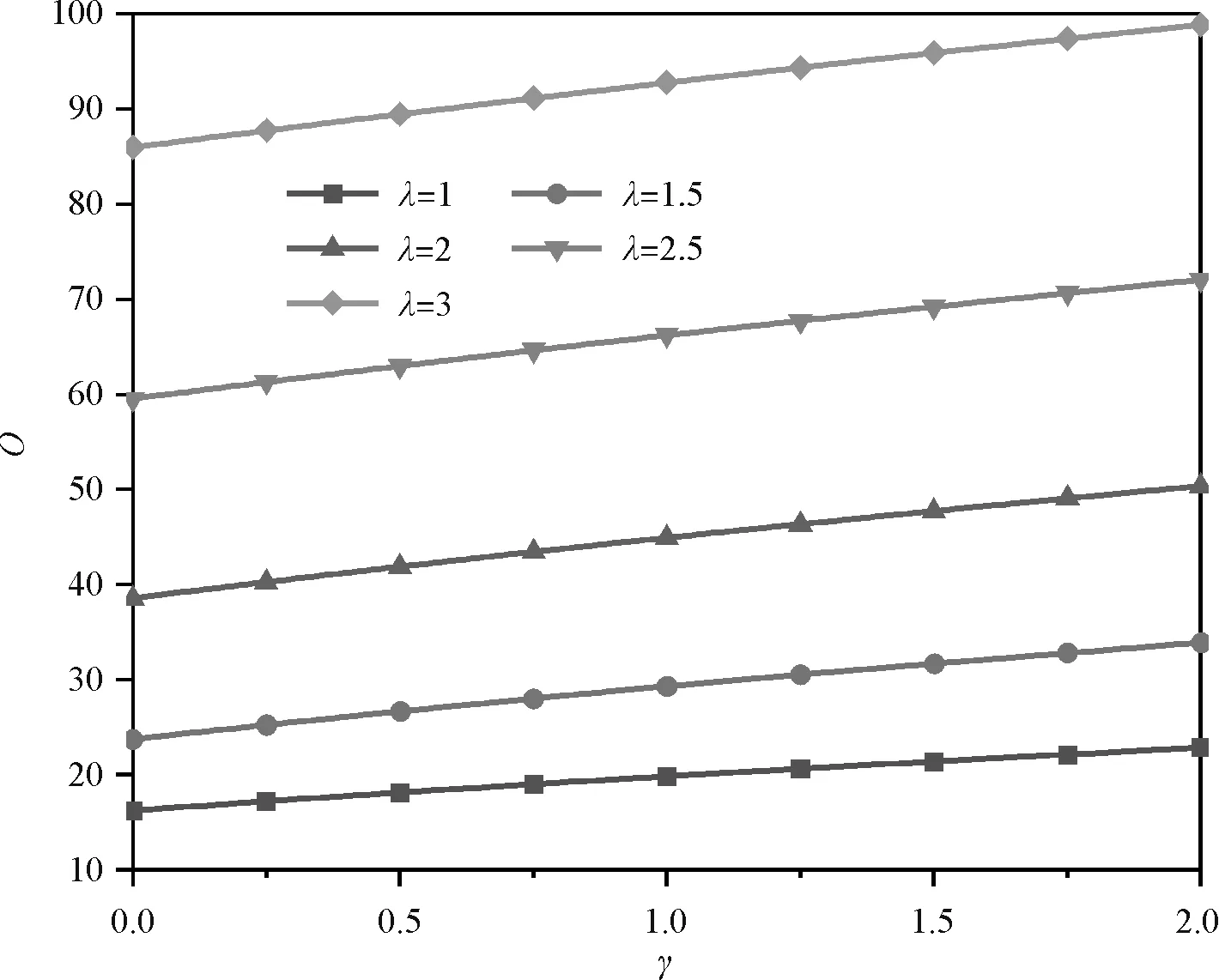
(c)SSCS边界条件
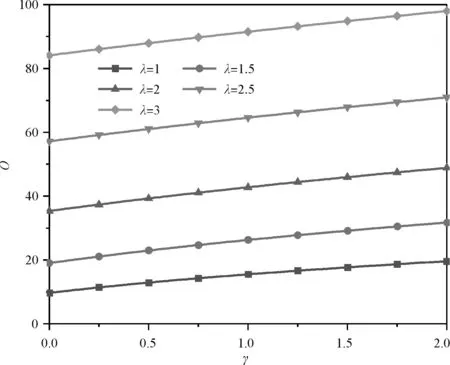
(d)SSSS边界条件
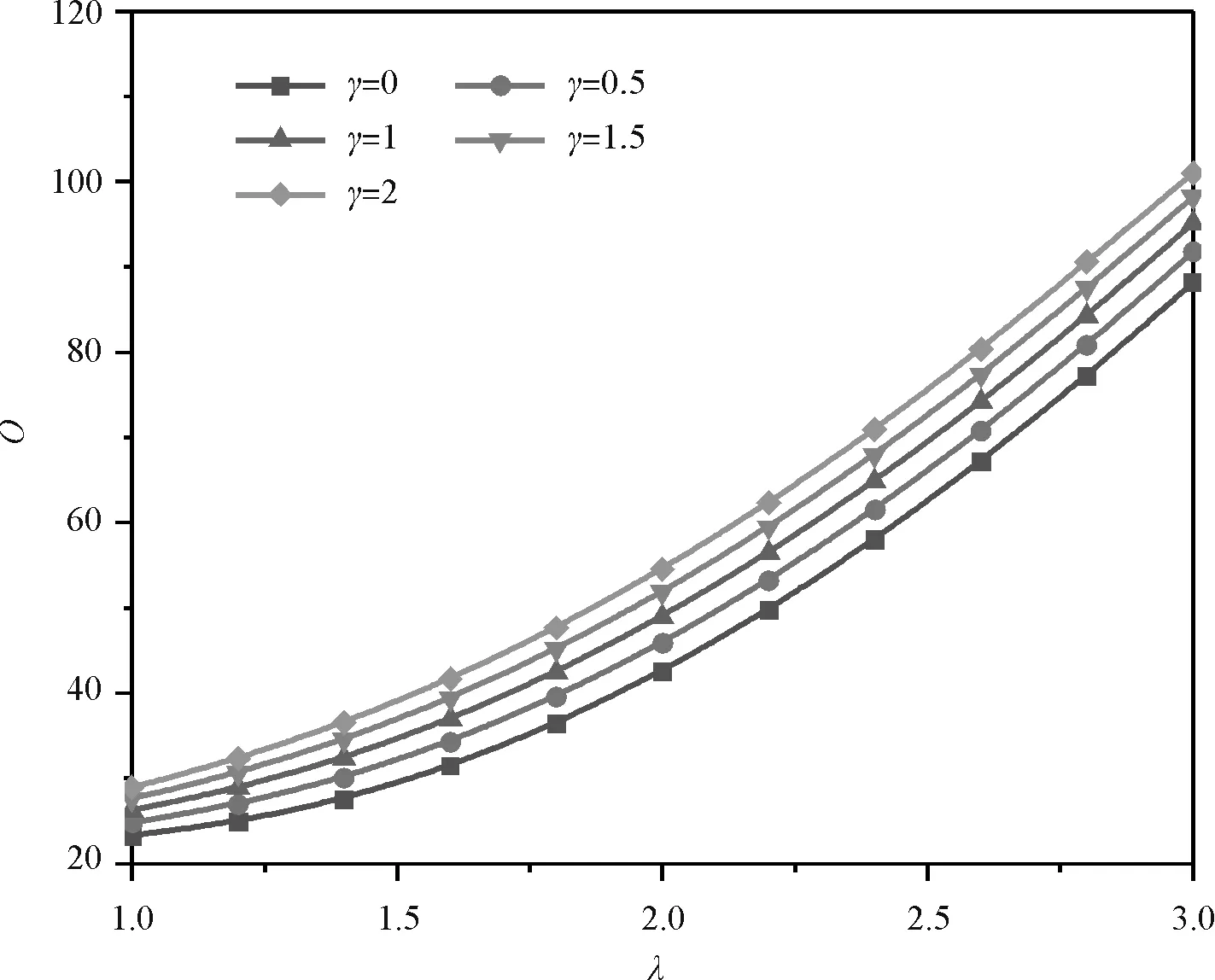
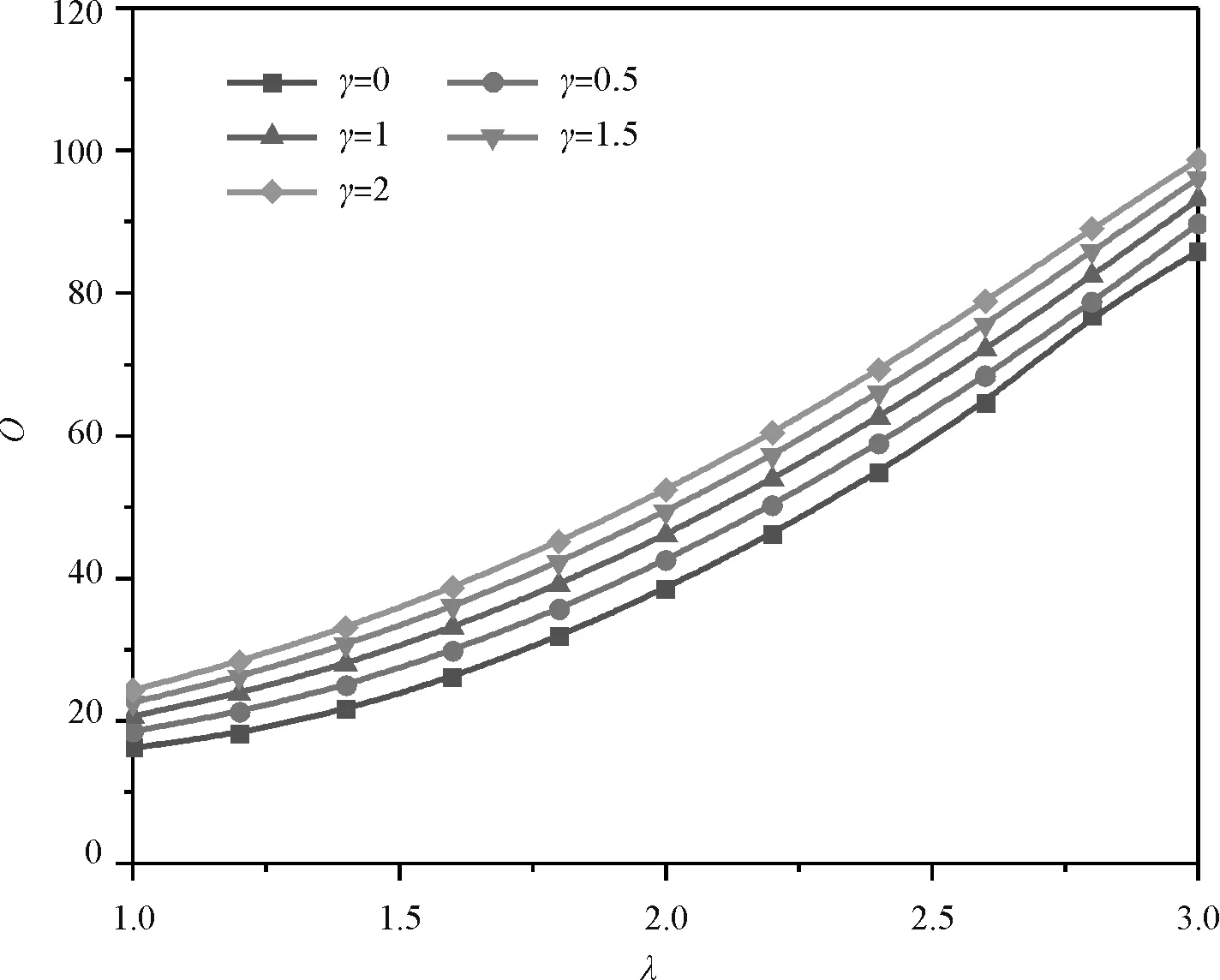
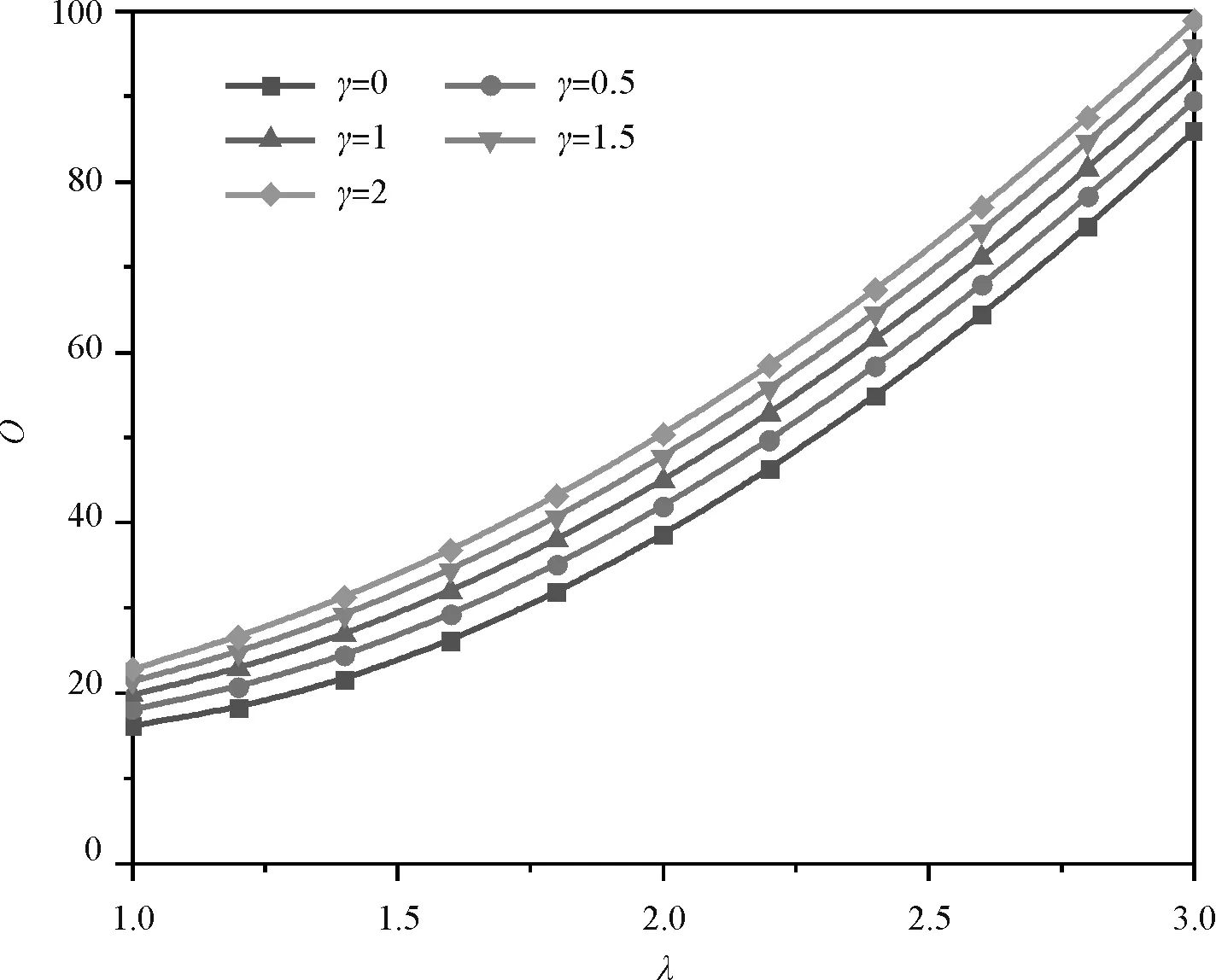
图3为N0*=30,m=1,H=0.1时,在CSCS、CSSS、SSCS、SSSS边界下1阶无量纲固有频率Ω与载荷参数λ的关系曲线。各边界下的Ω都随λ的增大而增大;约束较强边界下Ω较大(顺序:CSCS边界下频率值>CSSS边界下频率值或SSCS边界下频率值>SSSS边界下频率值)。
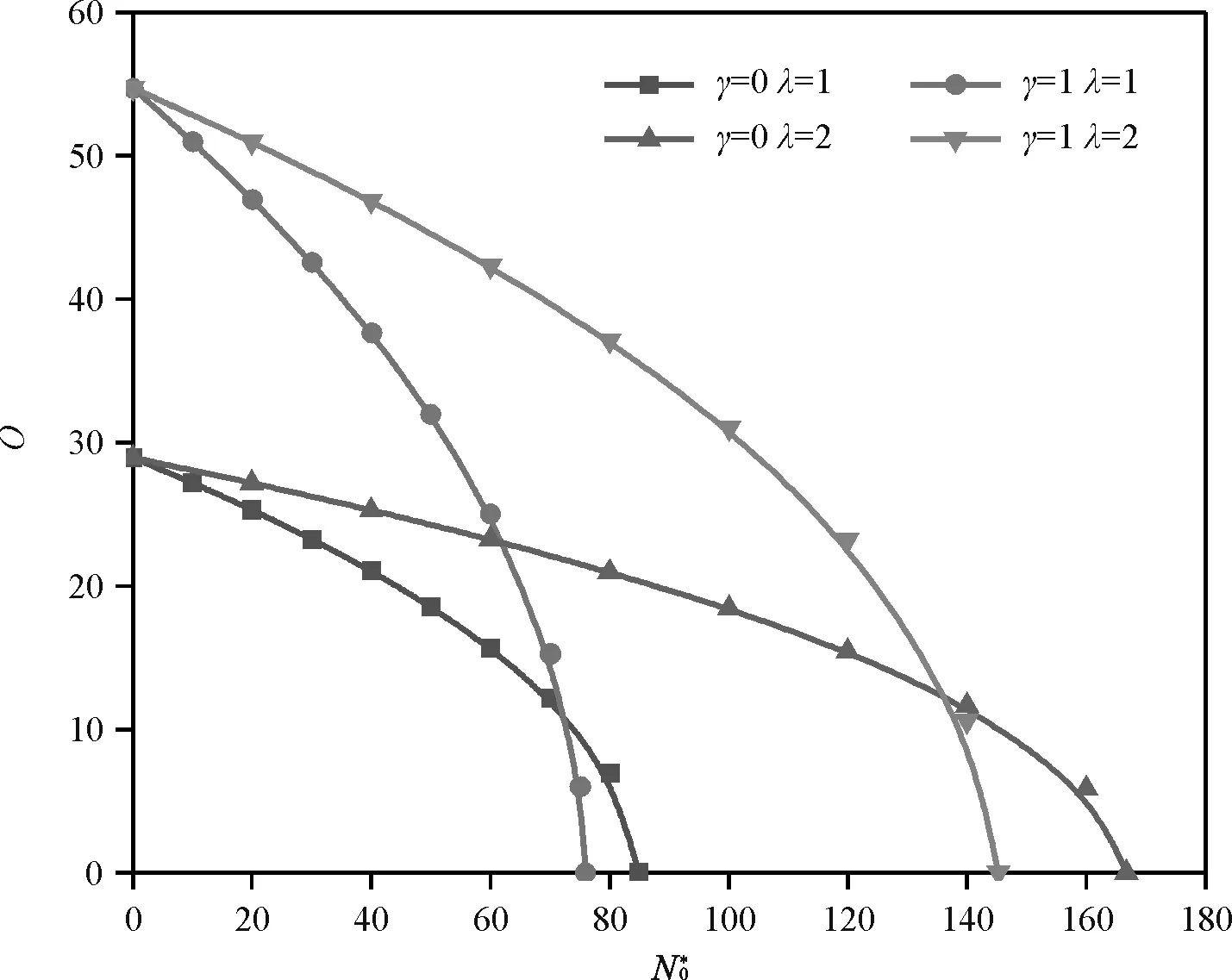
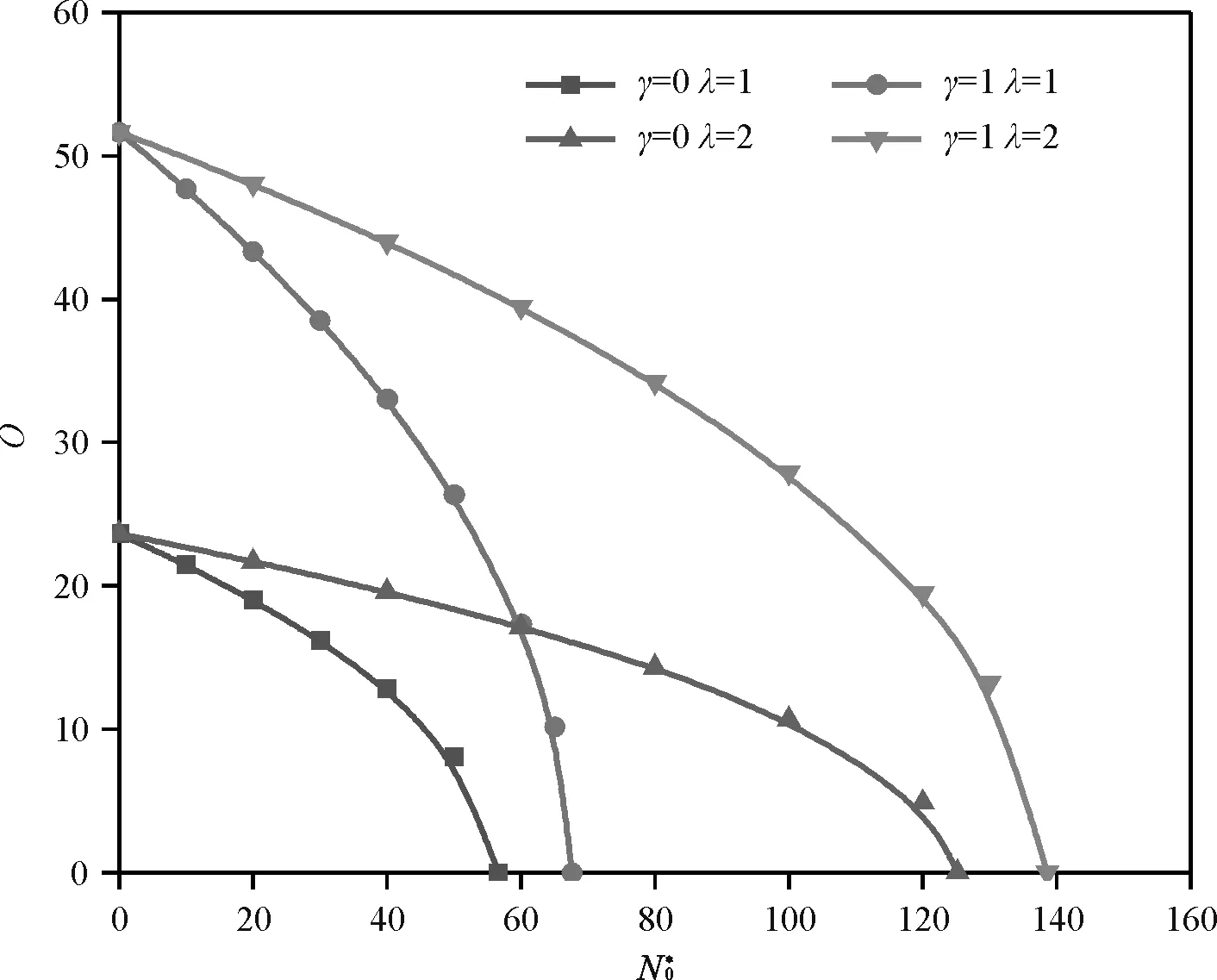
图4给出了不同参数下在CSCS、CSSS、SSCS、SSSS边界下1阶无量纲固有频率Ω与X=0处无量纲压力强度N0*的关系曲线。由图可见:当γ、λ,一定和H=0.1时,各边界下的Ω都随N0*的增大而减小且减小至0;当γ、λ及H=0.1、Ω=0时,N0*即为临界屈曲载荷Ncr并且约束较强边界下临界屈曲载荷Ncr较大(顺序:CSCS边界下临界屈曲载荷值>CSSS边界下临界屈曲载荷值或SSCS边界下临界屈曲载荷值>SSSS边界下临界屈曲载荷值)。
(a)CSCS边界条件
(b)CSSS边界条件
(c)SSCS边界条件
(d)SSSS边界条件
(a)CSCS边界条件
(b)CSSS边界条件
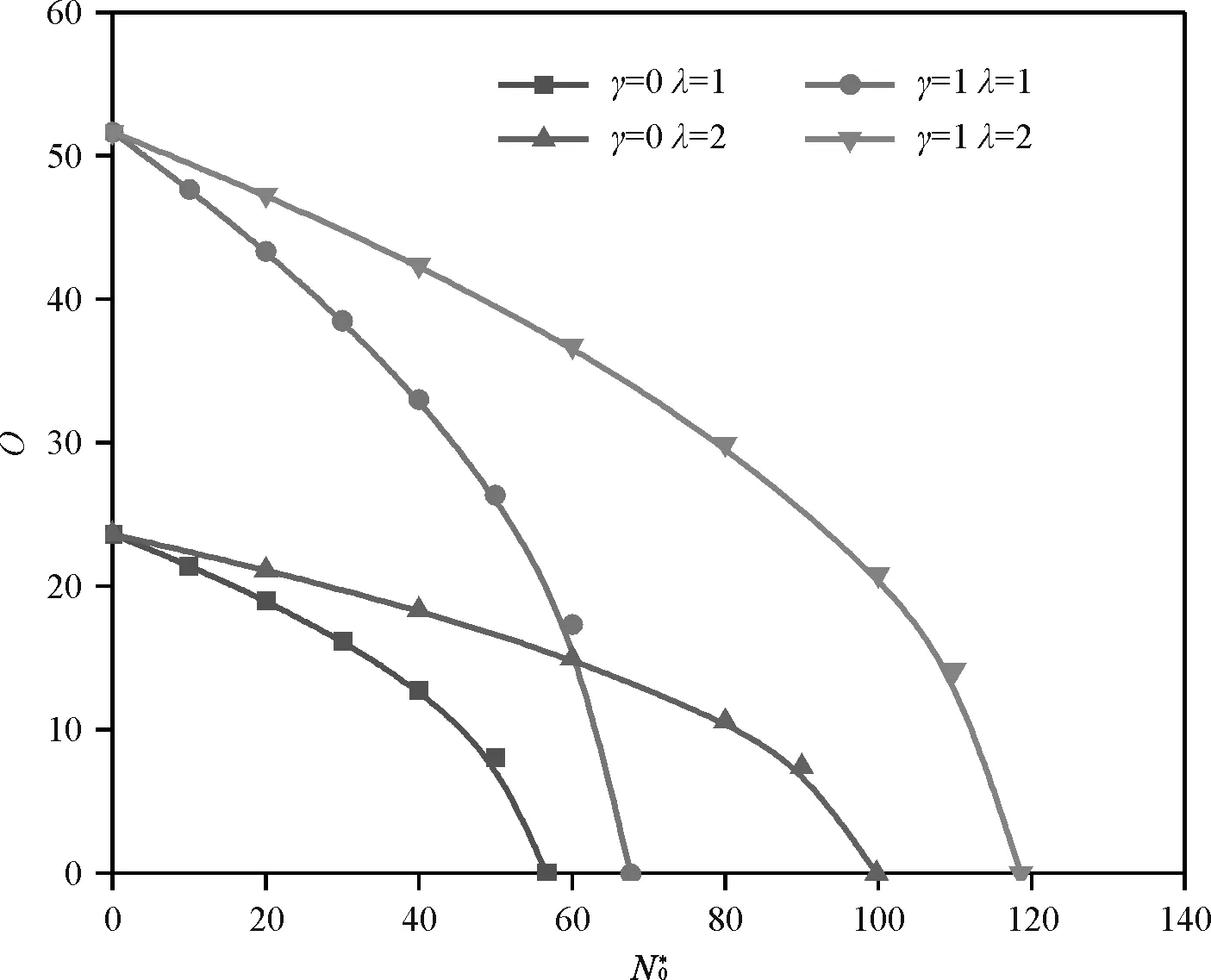
(c)SSCS边界条件
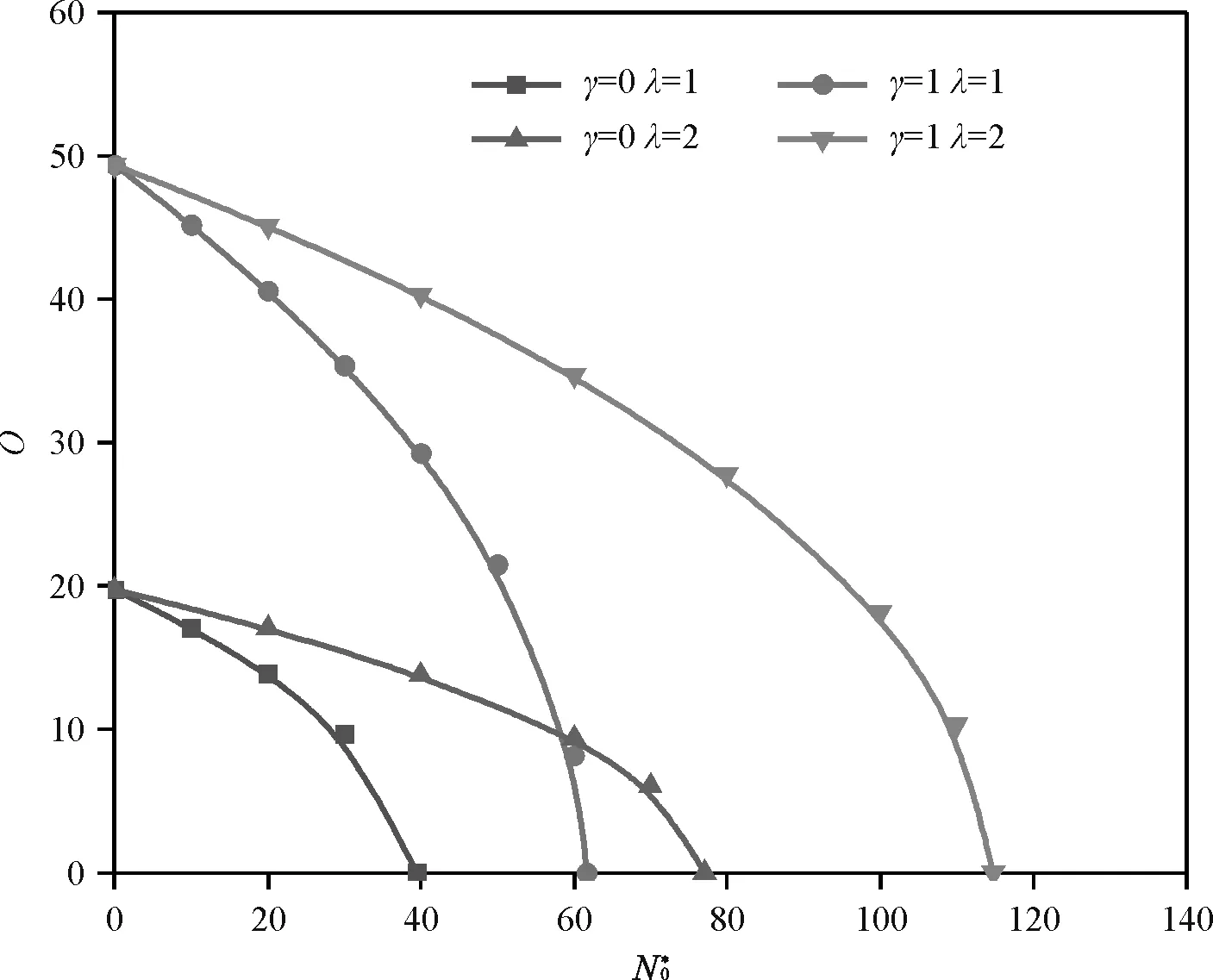
(d)SSSS边界条件
4 结论
本文基于经典薄板理论,利用Hamilton原理推导了面内受压大跨度混凝土板自由振动和的控制微分方程并进行无量纲化,采用DTM求解并研究了大跨度板的自由振动。考虑各参数对不同边界条件下大跨度板的自振频率Ω的影响。主要结论如下:
(1)随着载荷参数γ的增大导致了混凝土板系统受到垂直于y轴截面上的面内分布力Ny减小,从而使得大跨度混凝土板的自振频率Ω和临界屈曲载荷Ncr都增大。
(2)随着压力强度N0*的增大,从而使得基频Ω减小,当基频Ω=0时,意味着混凝土板系统发生失稳,此时的N0*为最危险的载荷,即为临界屈曲载荷Ncr;各边界条件下基频Ω都随长宽比λ的增大而增大,并且增大速率逐渐变大且较强约束的边界条件下自振频率Ω较大。
(5)本文深入分析大跨度混凝土板在面内荷载等多种载荷作用下的力学响应具有理论研究意义和工程实际应用价值。为路面混凝土结构、桥梁、楼板和地铁车站设计以及现场施工提供可靠的依据。
