某重型载货汽车车架柔性化建模及疲劳分析
2020-07-212
2
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.河北省交通安全与控制重点实验室,河北 石家庄 050043)
随着重型载货汽车在交通运输行业里应用越来越广泛,重型载货汽车的安全性受到了更多的重视[1]。车架是整个载货汽车的基体,汽车绝大多数部件和总成都是通过车架来固定其位置的。车架的功用是支承连接汽车的各零部件,并承受来自车内外的各种复杂动态载荷。重型汽车长期在满载状态下运行,条件恶劣,使用工况复杂多变,车架很容易发生疲劳破坏而导致整车无法正常行驶,甚至危及人们生命安全。因此对车架的刚度、强度以及疲劳特性进行研究就显得尤为重要。车架的疲劳可靠性是研究轻量化的基础,也是评价汽车性能的主要指标之一[2-4]。近年来,国内外学者对汽车车架的疲劳可靠性分析做了大量的研究,利用多体动力学仿真软件、专业的疲劳分析软件以及不同的疲劳设计方法相结合的方式对车架进行疲劳分析[5-9]。但是,目前对于重型载货汽车的动力学研究,多将除了悬架弹簧和减震器外,其余部件均当作刚性体来处理。但如果考虑构件变形对结果的影响以及构件应力大小、分布和载荷输出的时候,就需要将构件当作柔性体对待,既能保证模型的准确性、还原实际工况,又能使计算结果更加准确,更好地反映各个零部件之间的连接和受力关系。
1 柔性车架有限元模型的建立

图1 车架总成三维模型
以东风牌某重型三轴载货汽车车架为研究对象,该车架是由2根纵梁和11根横梁组成,车架长为11.398 m,宽为0.86 m,高为0.302 m。利用三维软件建立车架的各零部件,组装车架模型,为了防止车架上的一些次要零部件和工艺圆孔对车架的静力学分析产生影响,对车架进行了结构设计上的简化处理。把所有的倒角和过渡圆角简化成直角,删除部分对车架应力和应变影响较小的工艺辅助件,这是结构工艺的要求,对结构的强度和刚度影响不大,从而避免车架在有限元分析中因计算量过大,几何信息的报错对车架分析质量的影响。简化后的车架总成三维模型如图1所示。将三维软件建立的车架模型另存为.x_t格式导入到ANSYS中,对车架定义单元类型,若无特殊要求,通常为实体所添加的单元均为线性的八节点的六面体单元,单元1:solid45;单元2:MASS21。定义好单元类型,需设置车架的材料特性,如弹性模量、泊松比、密度等参数。
网格划分之后需要对车架创建关键点及刚性区域,建立关键点,其实是建立ADAMS中的外部节点,在ANSYS中指的是柔性体与刚性体连接位置的节点,用于在ADAMS整车模型组装中连接柔性体与刚性体。一般来讲,一个关键位置对应一个节点作为外部节点,因此该车架所用的外部节点是ADAMS/car中车架与整车用于信息交换的通讯器连接点,其中包括与驾驶室、转向系统、制动系统和发动机等的连接。刚性区域的建立,是ADAMS作为和外界连接的不变形区域,用来传递力的信息,如图2所示。最后,利用ANSYS输出ADAMS可识别的.mnf文件。

图2 建立外部节点车架模型
2 车架静强度计算与分析
通过对车架的有限元静强度分析,可以得到车架在不同工况下各个部位的应力分布和位移情况。典型的静力分析主要包括弯曲工况、扭转工况、急转弯、紧急制动4种常见工况。其中弯曲和扭转2种工况对实际运行中的车架结构影响较大[10],因此,主要研究车架在静态特性中的疲劳分析,对车架满载弯曲、满载扭转以及满载弯扭3种典型工况进行计算。研究的是6×4的三轴重载汽车,其后悬架为等臂式平衡悬架,前悬架钢板弹簧与吊耳连接,因此在施加约束时选择纵梁的连接件吊耳与平衡轴作为约束位置。
2.1 满载弯曲工况静力分析
满载弯曲工况模拟的是重型载货汽车在满载状态下,所有车轮完全着地,在较好的路面上匀速直线行驶的情况,从而研究车架在满载状况下的抗弯曲变形的能力。为了更加贴近车架在该工况下受载的实际情况,选定满载弯曲工况下的动载系数为2.5。约束前悬架左侧钢板弹簧的垂向平动自由度UZ,释放纵向自由度UX、横向平动自由度UY和3个旋转自由度;约束前悬架右侧钢板弹簧3个方向的平动自由度,释放3个旋转自由度;约束后悬架中、后轴左轮垂向平动自由度UZ,释放其他5个自由度;约束后悬架中、后桥右轮横向和垂向平动自由度UY、UZ,释放其他4个自由度。其分析结果如图3和图4所示。

图3 满载弯曲工况车架应力云图
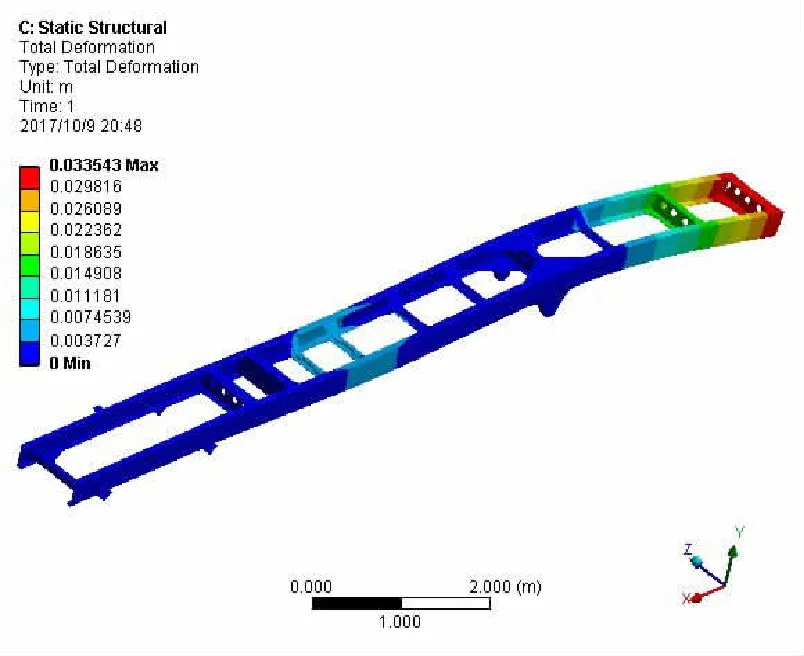
图4 满载弯曲工况车架位移云图
可以看到,在满载弯曲工况下最大的应力值在车架2根纵梁的后端与第8根横梁交接处,最大应力值为196.46 MPa。从满载弯曲工况车架位移云图可以看到,车架的最大变形量发生在2根纵梁的末端与最后1根横梁,最大变形位移为33.5 mm,因为车架尾部较长,车架后端承受外部载荷较大。
2.2 满载扭转工况静力分析
扭转工况是指重型载货汽车在不平路面行驶过程中受到非对称载荷作用力时,该重型载货汽车车架应力和变形分布。当汽车行驶在不平路面上,车架容易发生扭转,车架的强度和刚度会随之发生变化。满载扭转工况的约束情况为:约束右前轮3个平动自由度UX、UY、UZ;约束右中、后轮的横向和垂向平动自由度UY、UZ;约束左中、后轮的垂向平动自由度UZ,给左前轮一个10 mm的垂直向上的强迫位移,释放其余的自由度。分析结果如图5和图6所示。
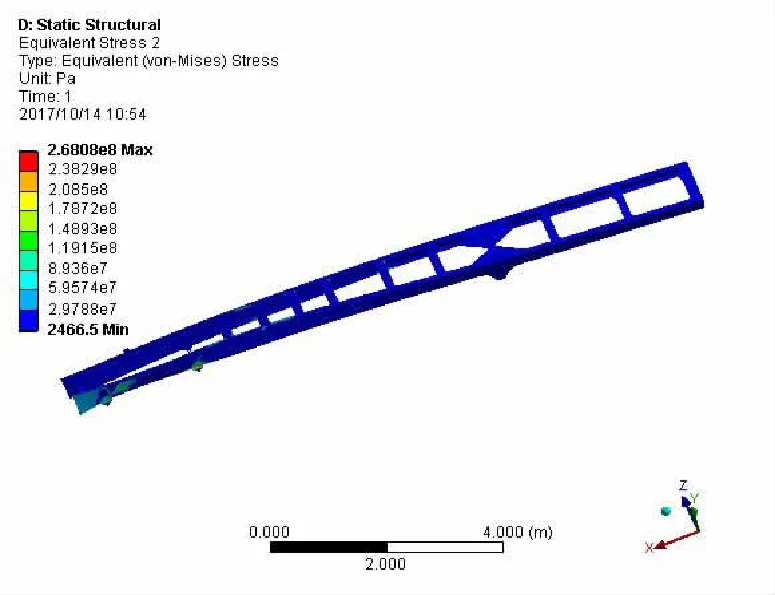
图5 满载扭转工况车架应力云图
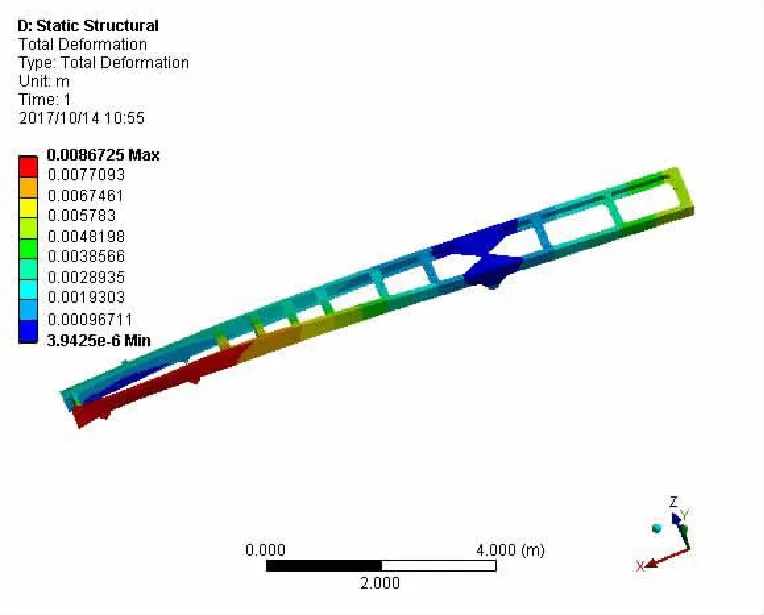
图6 满载扭转工况车架位移云图
从满载扭转工况车架的应力云图可以看出,车架的最大应力为268 MPa,发生在前悬架与钢板弹簧悬架系统相连接的后吊耳处,由于在前桥左轮处施加了10 mm的强迫位移,因此吊耳处发生了应力集中。从满载扭转工况车架位移云图可以看出,车架的最大位移发生在第一根横梁与左纵梁的连接处,为8.67 mm,发生了翘曲。
2.3 满载弯扭工况静力分析
满载弯扭工况是汽车在运行过程中所经历的最恶劣的行驶工况,它模拟的是车架的左前轮和右后轮同时抬起一定位移的工况。约束情况为:给前桥左侧车轮和中、后桥右侧车轮各一个10 mm垂向强迫位移;约束前桥右侧车轮的3个平动自由度UX、UY、UZ;约束中后桥左侧车轮横向和垂向平动自由度UY,UZ,释放其他自由度。分析结果如图7和图8所示。
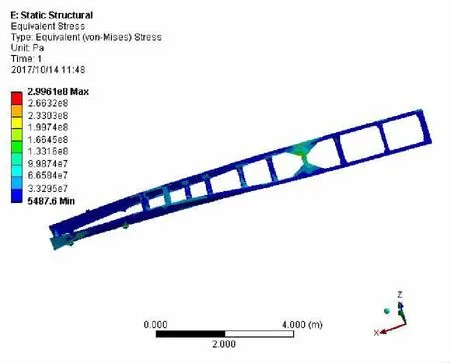
图7 满载弯扭工况车架应力云图
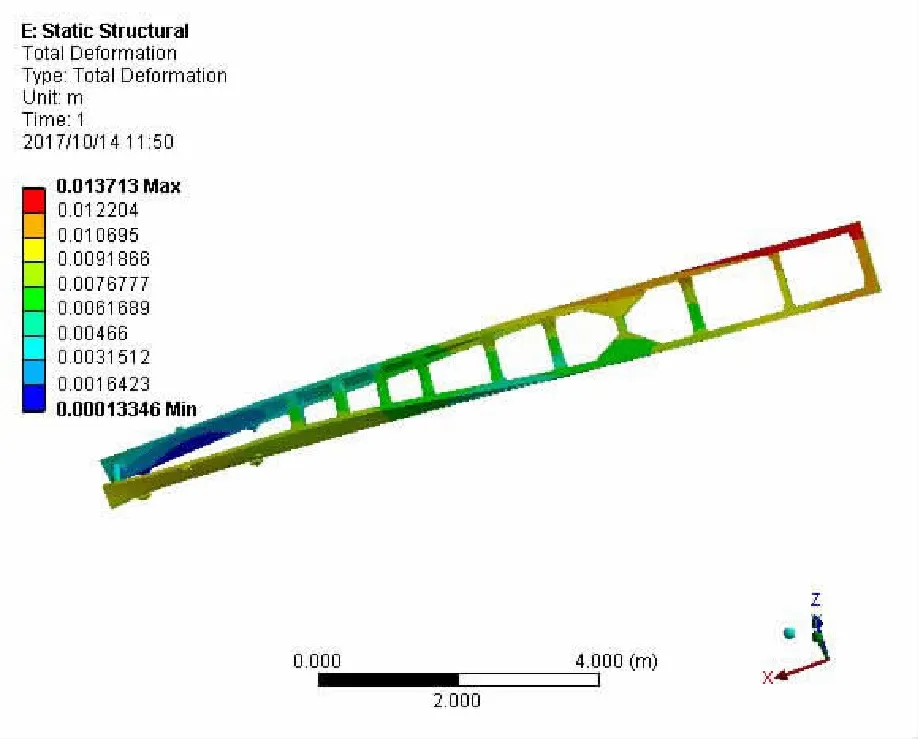
图8 满载弯扭工况车架位移云图
从满载弯扭工况车架应力云图中可以看出车架在满载弯扭工况下的最大应力出现在第八根横梁和右纵梁的吊耳连接处,最大应力为299.6 MPa,由于在中后桥处施加了10 mm的强迫位移,吊耳与纵梁采用了刚性连接,吊耳处发生了应力集中。从满载弯扭工况车架位移云图中可以看出,车架最大位移发生在最后一根横梁和右纵梁的连接处,大小为13.7 mm。
2.4 车架的强度校核
为了使车架满足汽车在行驶过程中所需要的强度要求,有必要对车架进行强度校核,控制车架的局部应力不能超过材料的屈服极限,车架的安全系数计算公式为
(1)
式中,σs为车架材料的屈服极限;σmax为车架最大应力值。当n>1时,表示车架在静载荷作用下的强度满足要求。
车架材料采用16Mn钢,俗称Q345钢,屈服应力为σs=345 MPa。车架在3种工况下的最大应力分别为σmax1=196.46 MPa、σmax2=268 MPa、σmax3=299.6 MPa,均小于材料的屈服极限σs。经过计算可得到,满载弯曲工况下的安全系数1.76,满载扭转工况下的安全系数1.29,满载弯扭工况下的安全系数1.15,安全系数均大于1,满足静载荷下的强度要求,为之后车架的疲劳分析奠定了基础。
3 刚柔耦合整车模型的建立与仿真
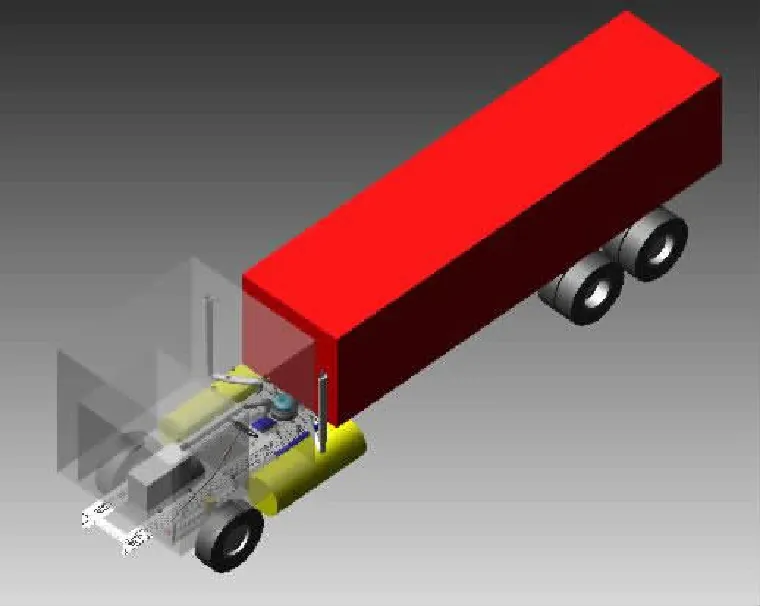
图9 刚柔耦合整车模型
通过有限元软件,将生成的车架.mnf文件导入Adams/car中,生成车架柔性体。建立柔性体与刚性体每个连接位置的哑物体,哑物体没有质量和惯性信息,不能直接与刚性体连接,因此在接口件处建立相应的通讯器[10],通讯器是一种基于模板模型的关键因素,用于子系统、模板、试验台之间数据的相互传递,最后生成柔性车架的模板及子系统。整车的建立除了柔性车架子系统之外,还需要前悬架子系统、后悬架子系统、转向系统、轮胎子系统、驾驶室子系统、制动及动力系统以及其他附件子系统组装而成。基于柔性车架组装成的刚柔耦合整车模型如图9所示。
选择刚柔耦合整车模型在满载工况随机路面下进行直线行驶仿真,在ADAMS/car中车速分别选择30~90 km/h,采用刚柔耦合整车分析方法,能够动态分析各种工况中柔性体的应力应变,可以为疲劳寿命分析提供更加准确的载荷数据。设置仿真时间为20 s,档位根据车速进行选择,总共提取了10个与车架相关的载荷谱,这里只列出了刚柔耦合整车模型车速为70 km/h时在随机路面下仿真得到的部分车架边界载荷谱,为后续的疲劳寿命分析载荷谱的输入奠定了基础,仿真结果如图10~图13所示。
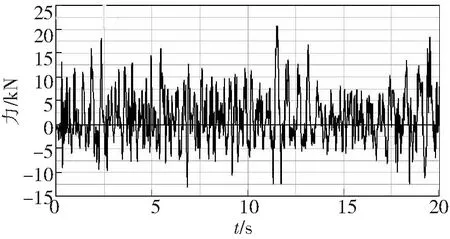
图10 前桥左侧减震器载荷谱
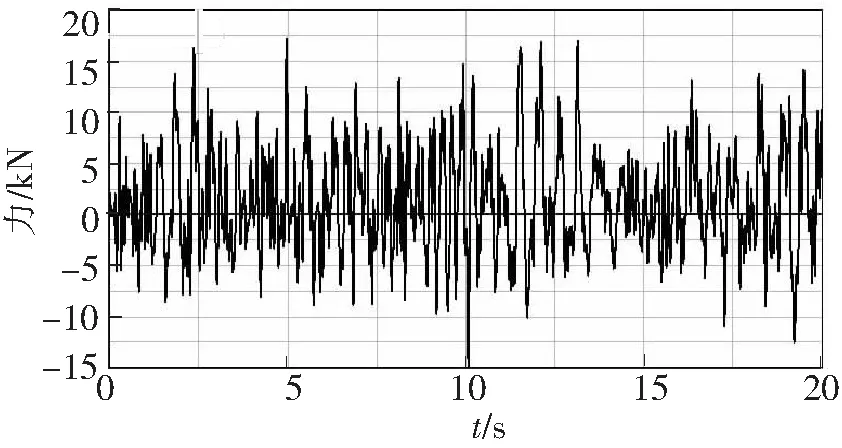
图11 前桥右侧减震器载荷谱
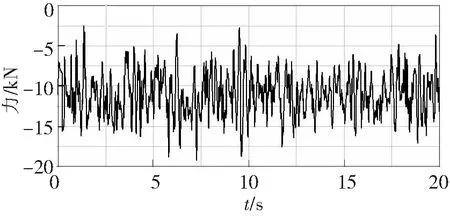
图12 中桥左下推拉杆载荷谱
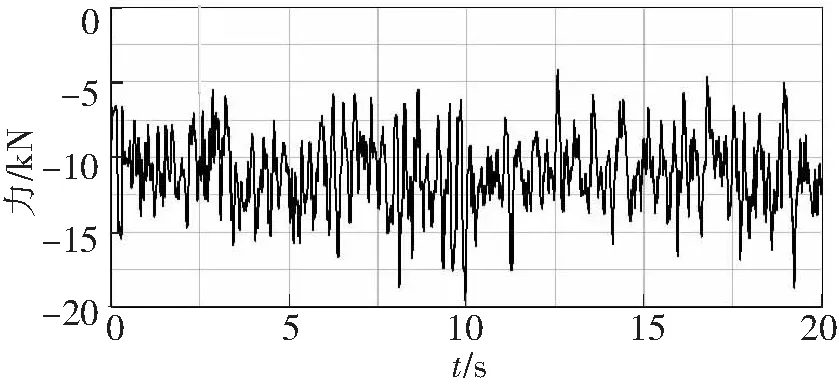
图13 前桥左侧减震器载荷谱
4 车架的疲劳寿命分析
4.1 定义车架的材料参数
车架属于高周疲劳,选择利用S-N法进行疲劳寿命分析。反应材料疲劳强度的特性曲线称为S-N曲线,分析车架疲劳寿命的前提是具有准确的材料疲劳特性参数。由于研究的车架材料并不在软件自带的材料库数据中,但nCode软件可以根据材料的抗拉极限和弹性模量来近似拟合。因此根据车架材料的弹性模量为210 000 MPa,泊松比为0.28,密度为7 700 kg/m3,屈服应力为345 MPa,抗拉强度为510~610 MPa,拟合出的曲线可用式(2)来表示。
S=SRI1(N)b
(2)
式中,SRI1为一插值,SRI1=2 849.64 MPa;b1=-0.155 1,b2=-0.084,其中,b1指的是循环次数在103~106之间直线的斜率,b2指的是循环次数在106之后直线的斜率。
4.2 不同工况及不同车速满载情况下的疲劳寿命分析
利用疲劳分析软件nCode Design-Life在对车架进行计算之前,需要在ADAMS/car中,将满载情况下30~90 km/h不同车速下的车架边界载荷谱导入到nCode Design-Life软件中,分别选取满载弯曲、满载扭转以及满载弯扭3种工况的分析结果作为有限元输入条件,并设置求解参数,进行求解计算,计算数据链如图14所示。
本文只列出了车速为70 km/h满载弯曲工况、满载扭转工况和满载弯扭工况下的疲劳寿命云图和损伤云图,如图15~图17所示。
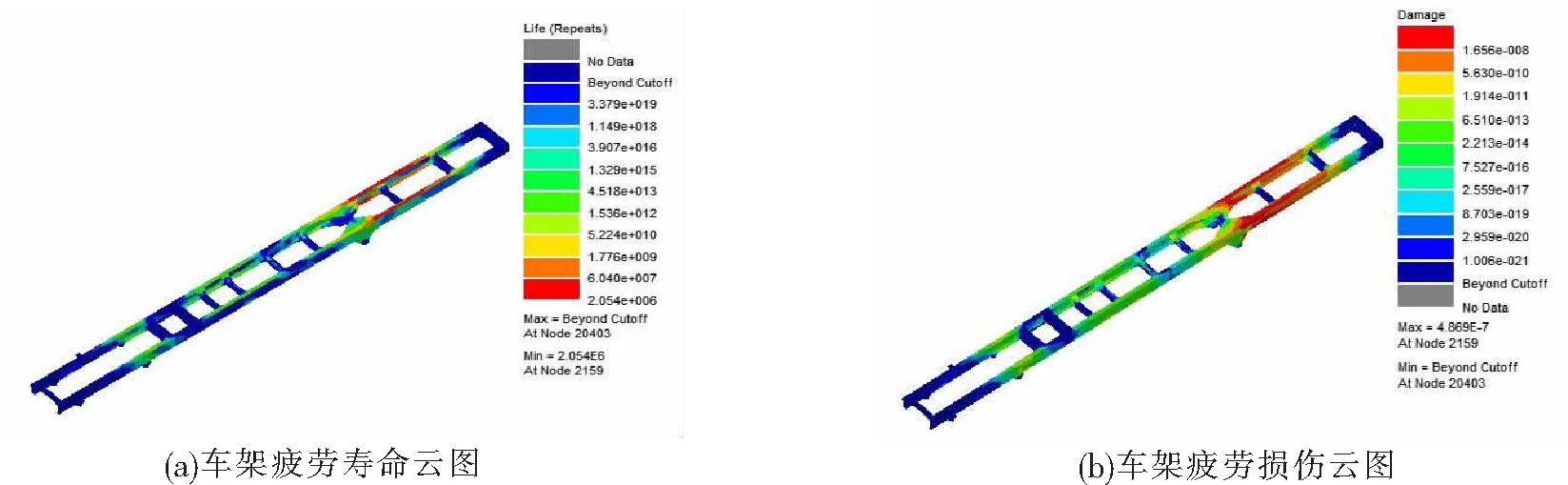
图15 满载弯曲工况下的疲劳寿命分析
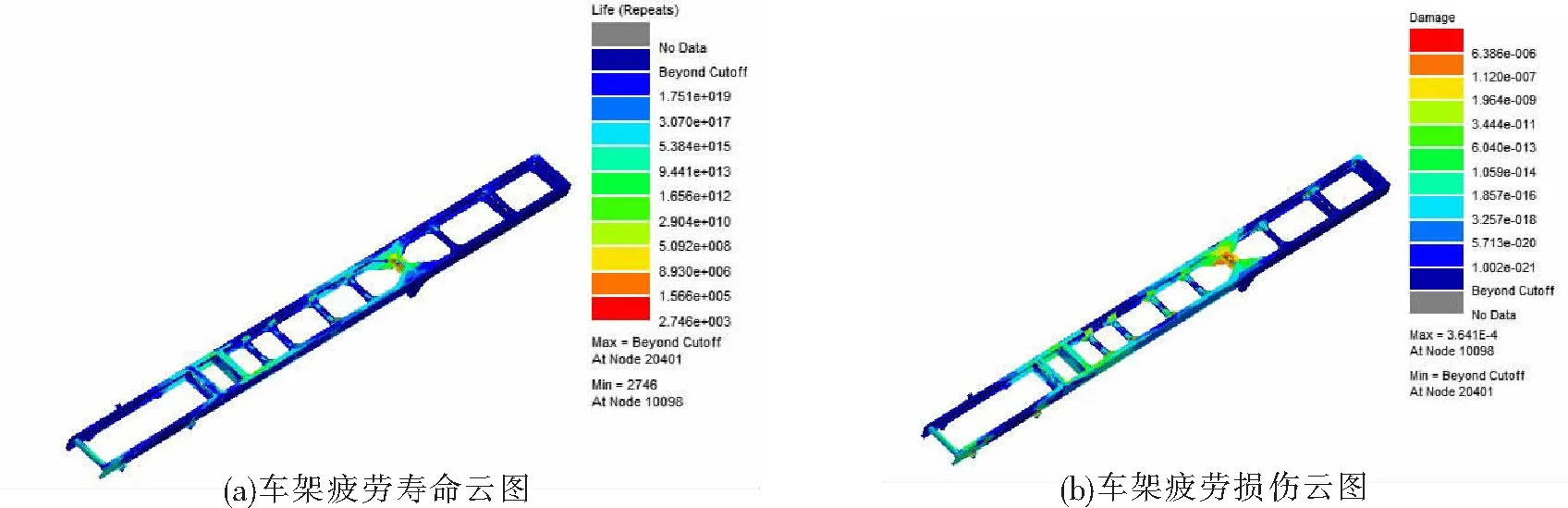
图17 满载弯扭工况下的疲劳寿命分析
从图15中可以看出,在满载弯曲工况下车架横梁与纵梁连接处有不同程度的疲劳累积损伤,特别是车架的中后桥第八根横梁与纵梁连接处损伤最为明显。根据2017年新实行的《机动车强制报废标准规定》第七条,国家对达到一定行驶里程的机动车引导报废第八小条明确指出重型载货汽车(包括半挂牵引车和全挂牵引车)行驶里程为70万km,结合本文研究车速为70 km/h,疲劳分析输入的载荷谱时长为20 s,计算得出该车架的疲劳循环次数为1.8E+006,而通过计算得出的该车架的最低节点的循环次数为2.05E+006,按照该节点最低循环次数疲劳寿命计算得出该车架的续航里程为79.72万km,因此该车架在满载弯曲工况下具有良好的抗疲劳特性和可靠性。
从图16中可以看出,在满载扭转工况下车架左纵梁前端与吊耳连接处损伤最为明显,最低循环次数为1.754E+004,已不能满足整车行驶里程标准,这是由于满载扭转工况是汽车在极度不平路面上行驶,车轮行驶到凸块或凹坑时使车架发生扭转,并且车架纵梁与吊耳的刚性连接导致局部应力集中。由于应力集中的原因在减震器与车架连接的部位也产生了疲劳损伤,虽然有局部少量危险节点,但是从2种工况下的疲劳寿命云图中可以看出,车架的绝大部分疲劳循环次数都大于1 019,趋近于无限寿命,局部危险节点对车架整体疲劳强度影响不大。
满载弯扭是汽车在行驶过程中遇到的最恶劣工况,车架才会发生弯扭变形,从而使车架的强度和刚度产生很大的变化,因此随着工况恶劣程度的不断增加,车架的疲劳寿命不断缩小。从图17中得到,在满载弯扭工况下,车架前端与吊耳连接处有不同程度的疲劳累积损伤,特别是车架的中后桥第八根横梁与纵梁连接处损伤最为明显。车架的最低循环次数为2.746E+003,显然不能满足整车行驶里程标准,这是由于应力集中所致。虽然局部存在少量危险节点,但是绝大部分疲劳循环次数都大于1 017,车架的疲劳强度还是符合要求。
本文还研究了车架在满载弯曲、满载扭转以及满载弯扭工况不同车速下的疲劳寿命,计算结果如图18~图20所示。
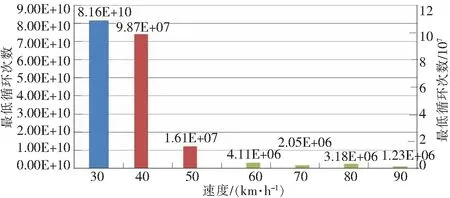
图18 满载弯曲工况不同车速下车架的疲劳寿命柱状图
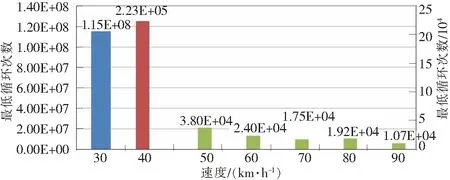
图19 满载扭转工况不同车速下车架的疲劳寿命柱状图
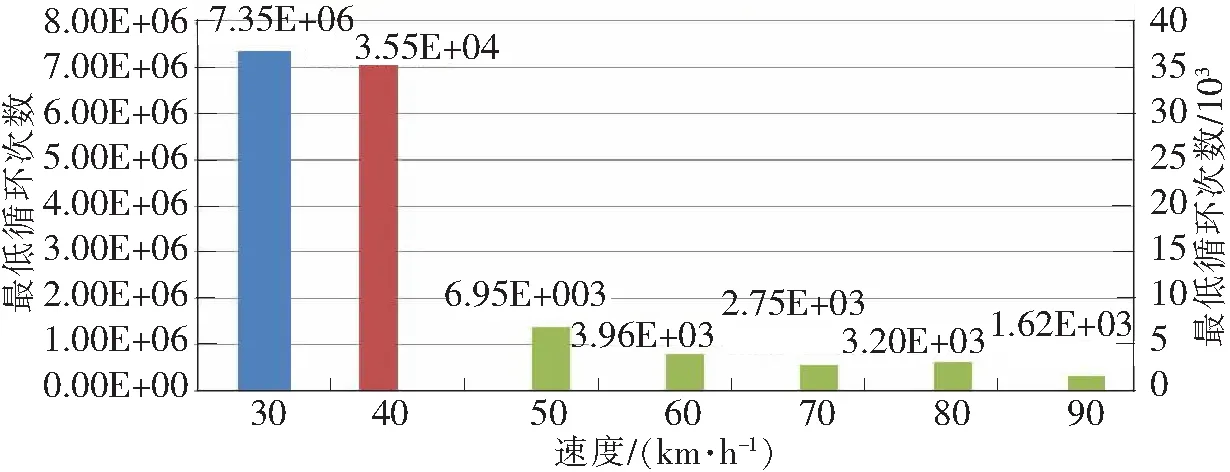
图20 满载弯扭工况不同车速下车架的疲劳寿命柱状图
从图18~图20可以看出:①随着车速的增加,车架所受到的载荷冲击逐渐增大,车架的疲劳寿命在不断缩减。②如图18所示,车架在满载弯曲工况下,车速为90 km/h行驶时,该车架的循环次数最低节点循环次数为1.23E+06,计算得出的续航里程为61.5万km,已经不能满足整车的行驶标准里程,但是重型载货汽车实际在正常行驶速度和工况下,很少长时间以90 km/h的速度行驶,因此该车架在满载弯曲工况下能够满足重型载货汽车正常的疲劳寿命要求。③如图19~图20所示,车架在满载扭转工况以及满载弯扭工况下,车速为40 km/h时,车架扭转工况最低节点的循环次数和弯扭工况最低节点的循环次数分别为2.23E+05和3.55E+04,已经不能达到整车的行驶标准里程数。但是从2种工况下的疲劳寿命云图中可以看出,车架的绝大部分疲劳循环次数都大于1 019,趋近于无限寿命,因此车架的强度是满足要求的。
5 结语
通过ANSYS和ADAMS/car软件的结合生成了车架柔性体,并建立了刚柔耦合整车模型。利用ADAMS/car虚拟仿真,更准确地得到了车架的边界载荷时间历程,为车架的疲劳分析做好准备工作。对于车架在3种满载工况下的研究,得到了车架容易产生疲劳破坏和损伤的危险节点及位置,并得到了车架在满载弯曲工况下能够正常满足重型载货汽车的行驶要求。虽然对于满载扭转和满载弯扭工况的分析,车架的最低循环次数并不能达到正常的行驶里程要求,但车架的绝大部分区域是趋近于无限寿命,而存在的少量危险点,对车架整体疲劳强度影响不大,因此本文研究的车架疲劳强度是符合要求的。该研究为重型载货汽车车架的疲劳分析提供了思路,并为接下来的车架优化奠定了基础。
