含有惯容的动力吸振器减振性能研究

( 石家庄铁道大学 机械工程学院，河北 石家庄 050043 )

0 引言

减少工程结构和机械设备中不必要的振动是设计过程中要考虑的重要因素，特别是对于受到外部激励的结构。为了减少振动对工程结构和机械设备的影响，学者们先后研究了被动控制、主动控制、半主动控制等方法来降低振动对结构的危害[1]。被动控制更多地应用在工程减振中，因为它们避免了主动和半主动控制的固有缺陷[2-3]，相比于主动控制，被动控制不需要输入外部能量，只需要通过阻尼耗能装置即可，且具有结构简单、便于维修、经济性好等特点。

自从1909年Frahm发明了动力吸振器[4](DVA， Dynamic Vibration Absorber)又称为调谐质量阻尼器(TMD，Tuned Mass Damper)以来，学者们对动力吸振器的研究已有百年历史。Frahm发明的无阻尼动力吸振器虽然能在外部激励和主系统频率相近时取得很好的减振效果，但该吸振器适用的频率范围较窄。在此之后，1928年Ormondroyd et al[5]发现在Frahm模型的基础上，在吸振器中加入阻尼可以有效地降低主系统的振幅并拓宽适用频率范围，该模型就是经典的Voigt型动力吸振器。Den et al[6]据此提出了固定点理论，该理论被广泛应用并且成为振动工程教科书中的经典结论[1]。Asami et al[7]提出了三要素DVA并给出了优化设计方案，减振效果明显优于Ormondroyd et al[5]提出的模型。2001年Ren[8]提出了一种接地DVA,根据固定点理论和H∞优化得到模型的最优参数，减振效果比Den和Asami et al提出的模型更佳。姚勇政[9]研究了多自由度动力吸振器的参数优化，并提出了计算机编程方法计算数值最优解的方法。Zhang J et al[10]研究了动力吸振器在能量收集方面的应用。

惯容是21世纪初Smith教授提出的一种具有2个独立的自由端点、且类似于弹簧和阻尼器的元件[11]，产生的力与其节点之间的相对加速度成比例。近些年来，学者们通过对惯容的研究发现其在减振、隔振方面有很好的应用。惯容最早应用在F1赛车悬架上，并取得了很好的效果[12]。Wang et al[13-14]把惯容应用在火车悬架上，提高了火车的稳定性和舒适性。Chen et al[15]等分析了惯容对隔振系统固有频率的影响。Hu et al[16]提出了6种ISD(I-Inerter，S-Spring，D-Dumper)结构并把其放在Voigt型DVA上，通过Matlab编程得到其最优参数。葛正等[17]研究了惯容动力吸振器在车辆悬架上的应用，可以有效改善乘坐舒适性。Barredo et al[18]研究了一种新型基于固定点理论的新方法优化含有惯容的DVA，得到其解析解。Shen et al[19]通过使用惯容将传统的DVA应用到车辆悬架上，使得悬架的指标有很大的提升。Luo et al[20]提出了一种新型电磁谐振分流器DVA，旨在最大限度地减少结构损坏的同时在随机风激励下收获能量，并在台北101大厦上实验成功。Wang et al[21]把惯容应用在经典动力吸振器上，使吸振器通过惯容接地，发现有很好的减振效果。

本文提出了6种含有惯容的动力吸振器，并通过计算机编程的方法[9]得到各个模型参数的最优解。

1 新型动力吸振器模型建立

1.1 惯容的动力学特性

惯容又称为惯性储能器或惯性质量储能器，与传统的弹簧和阻尼器一样具有2个独立的、自由的端点。当一对相互作用力作用于惯容元件2个端点时，两端点的相对加速度和作用力成一定的比例关系，该比例称作“惯容系数”，用字母b表示。理想惯容受力关系为

(1)

1.2 模型的建立和分析

图1所示是经典接地式DVA模型。图2是本文提出的惯容动力吸振器模型。图2中的结构A分别为图3中的6种ISD结构。其中m1、m2、b和c分别表示主系统的质量、吸振器的质量、惯容系数和阻尼系数；k1、k2和k3分别为各个模型主系统弹簧的刚度系数、吸振器上弹簧的刚度系数、ISD结构中的弹簧刚度系数;x1、x2分别为主系统位移、动力吸振器位移；x3为模型2、模型3、模型4、模型5、模型6阻尼与弹簧或惯容分割点的位移；x4为模型5中阻尼与惯容分割点的位移。Fsinωt是外界加载在主系统上的激励。根据牛顿第二定律得到如表1所示的动力学方程。

图1 接地式动力吸振器模型

图2 含有惯容的动力吸振器模型

图3 结构A中的6种ISD结构

表1 动力学方程及振幅放大因子

(2)

式中，i=1,2,3,4,5,6分别代表模型1、模型2、模型3、模拟4、模型5和模型6。式中的系数如下:

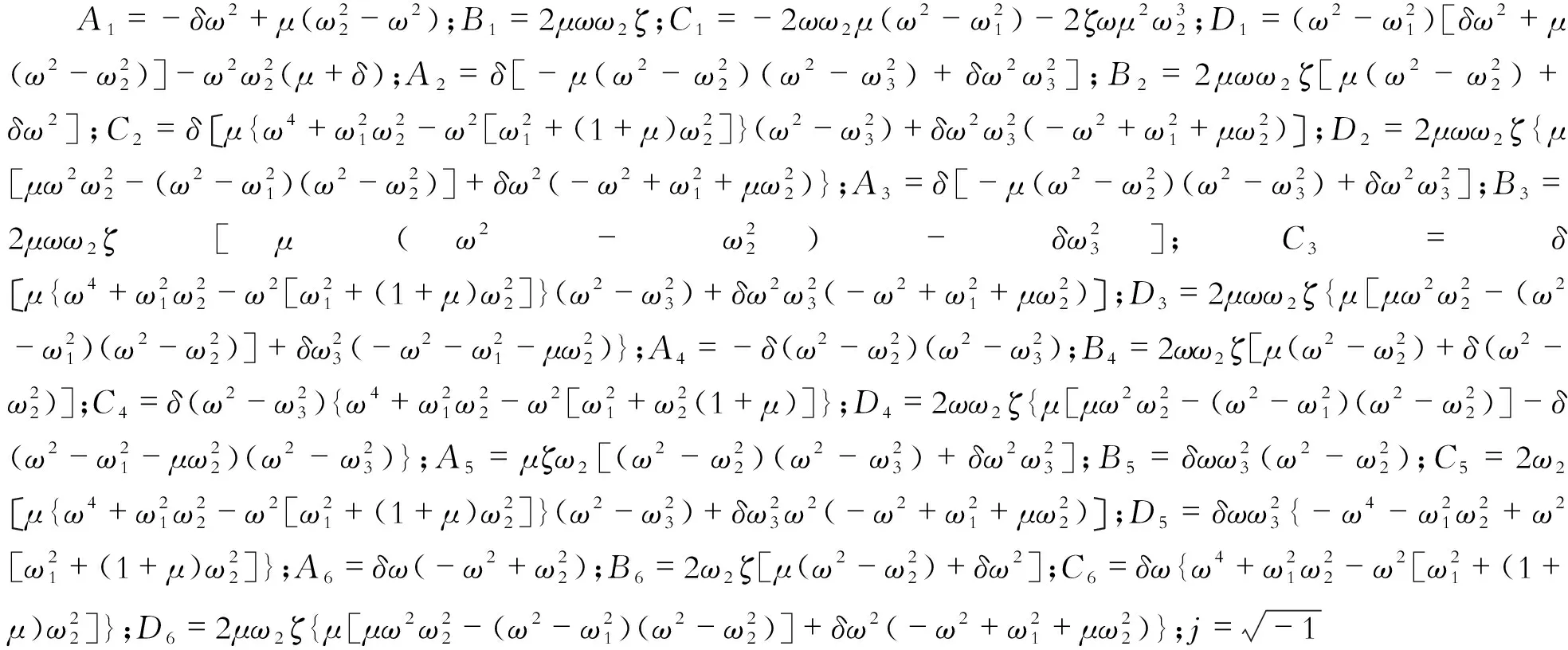
为了便于推导和计算，引入振幅放大因子，定义为

(3)

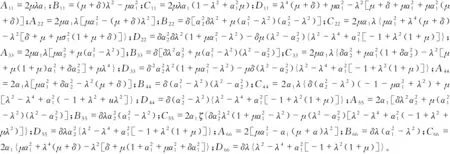
2 新型动力吸振器参数的优化

2.1 计算机编程寻优方法

固定点理论及H∞优化[6]是通过使目标函数最大值最小化来优化参数。两自由度的模型使用此方法可以轻松地求解出最优参数，但是2个以上自由度情况下，使用固定点理论及H∞优化便会极为困难甚至无法求解。本文提出的6种模型中，除模型1外，其他模型使用固定点理论及H∞优化便非常困难，因此使用了计算机编程寻优的方法。相比于文献[9],本文的计算机编程寻优方法思路更为清晰，编程环境由C++改为Matlab使计算速度大幅提高，计算精度更为可靠。

计算机编程寻找最优数值解的思路同H∞优化相似。将振幅放大因子ψi作为目标函数，其中频率比 为自变量，质量比μ、惯容比δ、固有频率比α1和α2、阻尼比ζ为需要优化的参数。程序设计思路为：给定一个μ+δ的值，对参数μ、δ、α1、α2、ζ在合理区间内划分小步长，得到μ、δ、α1、α2、ζ的各种组合集，使用计算机编程的方法寻找到每组参数组合对应的目标函数的最大值，通过比较求得目标函数最大值中的最小值，此时μ、δ、α1、α2、ζ的取值即为最优数值解，计算精度可以通过改变步长来实现。计算机编程寻优思路及步骤如图4所示。

图4 计算机编程寻优思路及步骤

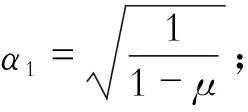
通过计算机编程寻优的方法，对经典接地式DVA进行参数寻优，得到最优参数的数值解。2种不同方法得出的结果对比及相对误差如表2所示。

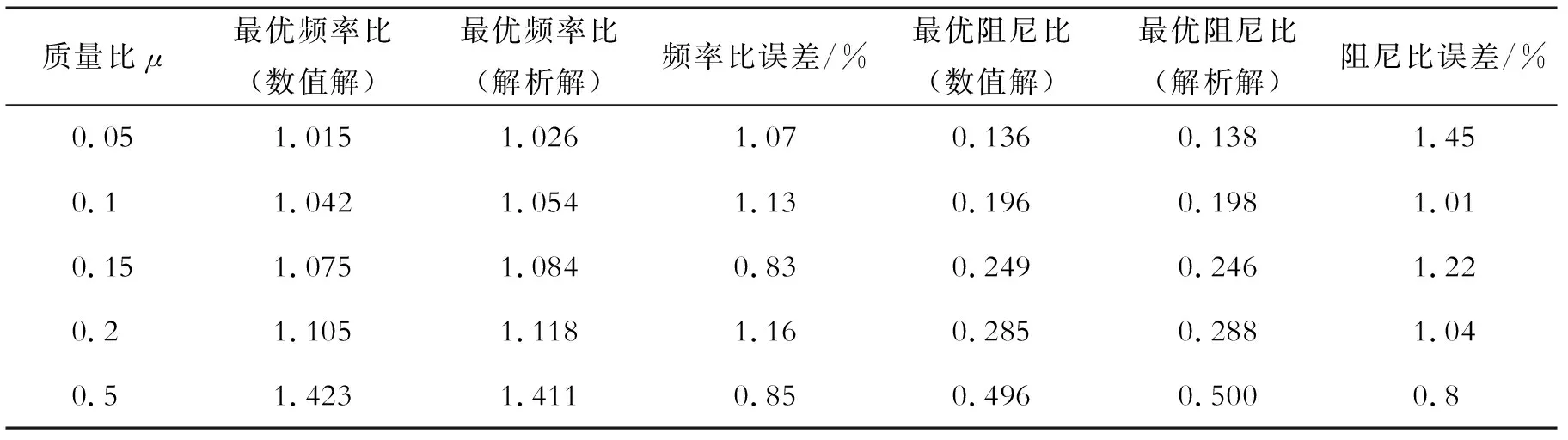
表2 接地式DVA使用2种方法的结果对比

通过比较发现，计算机编程寻优的方法得到的最优参数与解析解的最大误差不超过1.45%，证明了计算机编程寻优方法的正确性和合理性。

2.2 计算机编程优化结果

质量元件是单端点元件即必须有一点接地，惯容元件是两端点元件，由于惯容的力学特性，与加载在其两端的相对加速度成正比，有一定的质量特性，故把质量和惯容看做一个整体。因此在优化时，把μ+δ看做为一个整体。

在不同的给定参数μ+δ下，模型1、模型2、模型3、模型4、模型5和模型6使用此方法得到的最优数值解及振幅放大因子最大值如表3～表8所示。

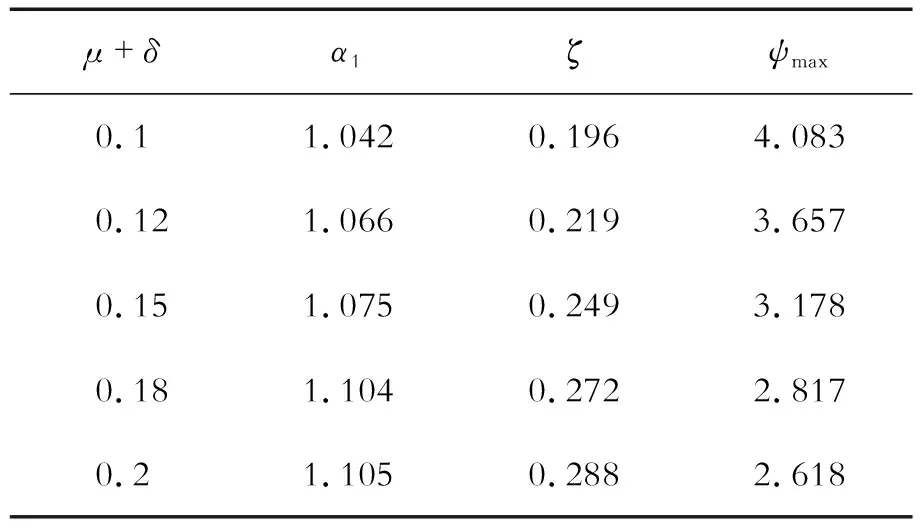
表3 模型1最优参数

表5 模型3最优参数

表6 模型4的参数优化结果

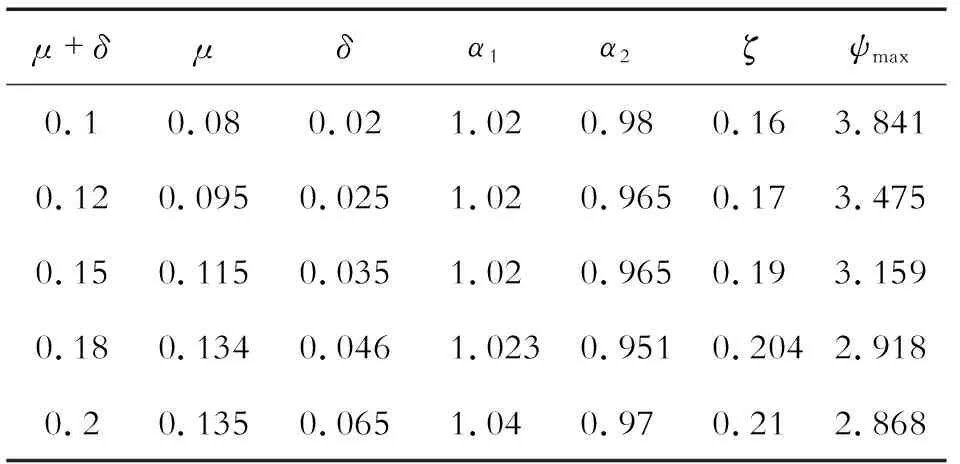
表7 模型5最优参数数

表8 模型6最优参数

从计算结果可以看出，模型1只需要保证μ和δ之和的值即可，不需要再对μ和δ进行优化。而其他5种模型则需要对μ和δ进一步分别优化。基于表3～表8得到的最优数值解，可以画出模型1～模型6的幅频曲线如图5～图10所示。从6种模型的幅频曲线中可以看出，随着μ和δ之和的增加，振幅放大因子随之降低。同样可以验证，在μ+δ取其他值时，有相同的结论。

图5 模型1的幅频曲线

图6 模型2的幅频曲线

图7 模型3的幅频曲线

图8 模型4的幅频曲线

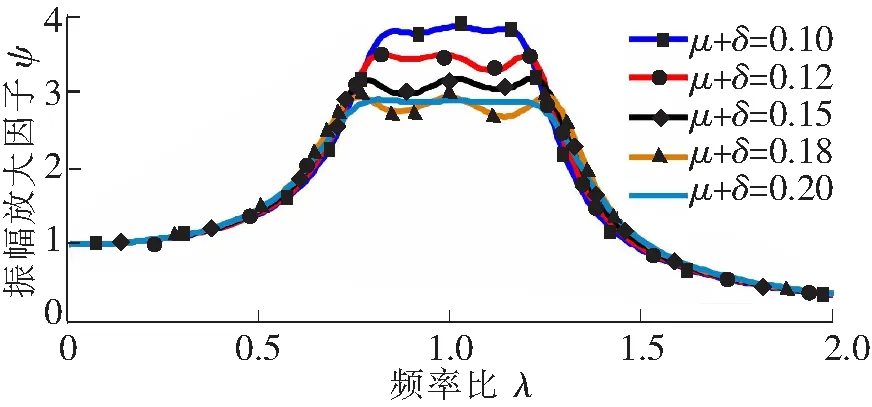
图9 模型5的幅频曲线

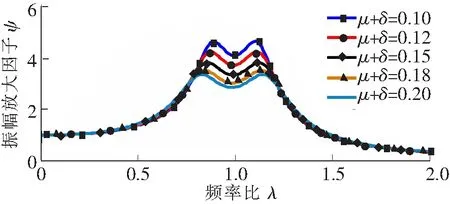
图10 模型6的幅频曲线

为了进一步验证在μ+δ取值一定的情况下，采用的数值方法优化结果相较于其他μ和δ的组合有更好的减振效果，现以μ+δ取值为0.1为例，比较不同的μ和δ的组合下的幅频曲线最大值。表9为不同的μ和δ组合幅频曲线的最大值。

表9 不同μ和δ组合幅频曲线最大值

从表9中可以看出，除模型1外，在μ+δ取值一定的前提下，μ和δ的其他组合会导致振幅放大因子的变大，表明了本文优化结果的正确性和合理性。同样可以验证，在μ+δ取其他值时，有相同的结论。

3 与传统动力吸振器的比较

3.1 简谐激励下的比较

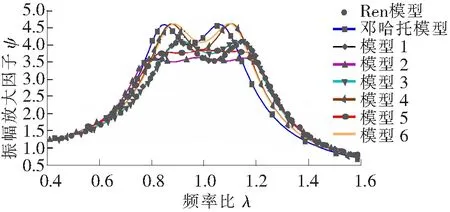
图11 简谐激励下的幅频曲线

为了研究提出的6种惯容动力吸振器的减振效果，将该6种模型与经典的动力吸振器(Voigt型DVA，接地式DVA)在简谐激励下作比较。这里假设接地式DVA的吸振器和主系统质量的比μ为0.1，模型1～模型6的块质量比μ与惯容比δ之和也为0.1。幅频曲线的比较如图11所示，幅频曲线最大值的比较及相对衰减率如表10所示。

表10 简谐激励下振幅放大因子最大值统计及相对衰减率

从图11及表10可以看出，本文提出的新型惯容接地DVA有一定的减振效果。其中模型1、模型2、模型3、模型5的减振效果均优于Voigt型DVA，模型2、模型5的减振效果优于接地式DVA，模型4、模型6与Voigt型DVA减振效果相当，模型1与接地式DVA减振效果相当，模型4和模型6的减振效果次于传统动力吸振器。可以验证，在μ+δ取其他值时，本结论仍然成立。

3.2 随机激励下的比较

因为在实际工程中系统所受的激励大都为随机激励，所以在随机激励下系统的响应有着很重要的意义。为了比较6种模型在随机激励下的减振效果，如图12所示，构建了50 s均值为0的随机激励。设定主系统质量块m1=1 kg，刚度k1=100 N/m，质量比μ和惯容比δ之和为0.1，其余参数可以根据表3～表8和文献[5，8]得到。图13为不含吸振器的主系统时间历程图，图14～图21分别为Voigt型DVA、接地式DVA、模型1、模型2、模型3、模型4、模型5、模型6的主系统时间历程图，主系统响应方差值统计及其相比于无吸振器时的衰减比如表11所示。

图12 随机激励时间历程图

图13 不含吸振器的主系统时间历程图

图14 Voigt型DVA的主系统时间历程图

图15 接地式型DVA的主系统时间历程图

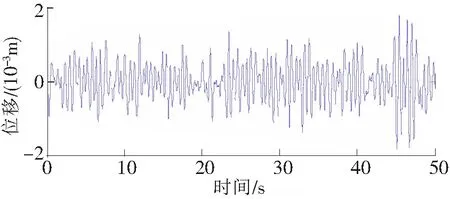
图16 模型1的主系统时间历程图

图17 模型2的主系统时间历程图

图18 模型3的主系统时间历程图

图19 模型4的主系统时间历程图

图20 模型5的主系统时间历程图

图21 模型6的主系统时间历程图

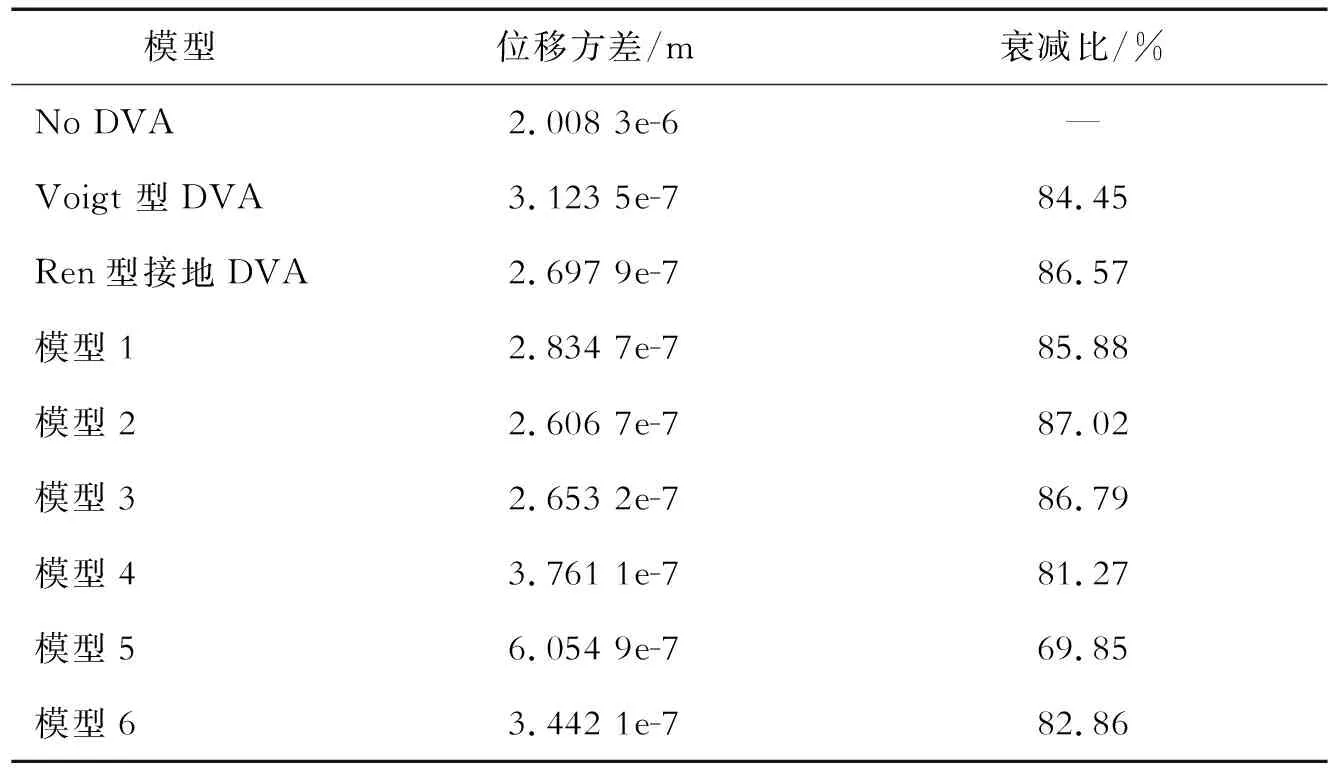
表11 主系统响应方差统计值及其衰减比

从图12～图21及表11可以看出，本文提出的新型惯容接地DVA在随机激励下仍具有一定的减振效果，其中，模型2在随机激励下减振效果最好。模型1、模型2、模型3的减振效果优于Voigt型DVA，模型2、模型3减振效果优于接地式DVA，模型4、模型5、模型6的减振效果次于接地式DVA和Voigt型DVA。可以验证，在μ+δ取其他值时，本结论仍然成立。

4 结论

本文提出了6种惯容-弹簧-阻尼结构，并把它们应用于接地型动力吸振器中。使用H∞优化思路通过计算机编程的方法寻找各个模型的最优参数的数值解，相比于H∞优化方法，计算机编程寻优方法对2个以上自由度的模型更为简单，而且精度可以通过改变编程的步长来实现，达到解析解想要达到的效果。通过对比证明了在μ和δ取值一定的前提下，本文优化出的μ和δ的组合减振效果明显优于其他组合。

通过与传统动力吸振器在简谐激励和随机激励下主系统响应的比较，发现本文提出的6种模型具有一定的减振效果。使用上述优化方法在简谐激励下，本文提出的6种模型的减振效果和经典DVA相比依次为：模型2、模型5、接地式DVA、模型1、Voigt型DVA、模型5、模型4、模型6，故在简谐激励下，使用图3中的2和5所表示的ISD结构代替接地式DVA中的阻尼，会使减振效果更好；随机激励下本文提出的6种模型的减振效果和经典DVA相比依次为：模型2、模型3、接地式DVA、模型1、Voigt型DVA、模型6、模型4、模型5，故在随机激励下，使用图3中的2和3所表示的ISD结构代替接地式DVA中的阻尼，会使减振效果更好。从上述对比中可以看出，增加一个自由度并以合适的ISD结构代替传统接地DVA中的接地阻尼可以增加减振效果，对新型动力吸振器的设计和改造有一定的指导意义。