构建立体几何模型，小议棱锥的外接球问题

◇ 甘肃 苟丫丫

与球相关的切接问题是高考命题的热点，也是考生理解上的难点、易失分点，命题角度多变，要求学生有较强的空间想象能力，在把握题意的基础上对要解决的问题有丰富的联想能力；在解决问题的过程中有良好的平面几何计算能力.在平时的教学中，教师应利用信息技术演示球的内接几何体，让学生有直观想象的依据.本文就棱锥的外接球问题做如下模型探讨.

1 补形法，简化问题求解

例1球面上有四个点P，A，B，C，满足PA，PB，PC 两两垂直，且PA=3，PB=4，，则球的表面积等于

分析在三棱锥P-ABC 中，棱PA，PB，PC 两两互相垂直，是本题解题的题眼.解决立体几何问题应多观察，多思考，大胆假设，小心求证.这样的三棱锥来源于以为长宽高的长方体，它们的外接球是同一个球体，而长方体的外接球问题学生是熟悉的.此时，球的直径是长方体的体对角线.

解析

图1

2 利用对称中心，直接求解

例2已知S-ABC 为棱长为a 的正四面体，求它的外接球的半径.

分析正四面体与它的外接球都是中心对称的几何体，故正四面体的中心既是它的外接球球心，又是它的内切球球心.如图2，M 为点S 在平面ABC 上的射影，即为△ABC 的中心，也是重心，球心O 在SM 上.

解析

图2

又有OM2+MB2=OB2，即

例3体积为的正四棱锥S-ABCD 的底面中心为O，SO 与侧面成的角的正切值为那么过SABCD 的各顶点的球的表面积是（ ）.

A.32π B.24π C.16π D.12π

分析设正四棱锥的底面边长为a，高为h，题设给出了正四面体的体积，有又给出SO 与侧面成的角的正切值为是底面边长a 和高h 的第二个关系式.根据两个条件，可求出底面边长a和高h，再去解决它的外接球问题.

解析

图3

方法1延长SO 交球面于点M，则S，B，M 均在球面上，且SM=2R，∠SBM=90°.

在Rt△SMB 中，由射影定理得

方法2同例2的解法，可得=4πR2=16π.

3 类比圆的性质，转化问题求解

例4如图4，在平面四边形ABCD 中，AB=将其沿对角线BD折成四面体A′-BCD，使面A′BD⊥面BCD，若四面体A′-BCD 的顶点在同一球面上，则该球的表面积为（ ）.

图4

分析先根据题意，得出折叠后四面体的特征，再解决它的外接球问题.

解析

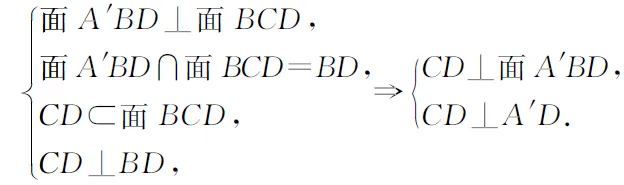
图5

类比圆，直径所对的圆周角为直角，那么内接于球的A′-BCD 中，BC 所对的两个角都是直角，故BC为球的直径.所以

点评

对于不同于例1、例2的四面体的外接球问题，要通过认真审题，研读题意，大胆猜想，小心论证，抓住特征，解决问题.

虽然棱锥的外接球问题题型多变，但只要抓住问题的实质，透过现象看本质，就能找出棱锥的特征，还是可类比圆的内接三角形问题.只有细心研读题意，紧密联系生活实际，正确归类问题，建立恰当的数学模型，才能顺利解决问题！