氯离子侵蚀下RC 框架结构时变抗震性能研究

周 炎，郑山锁，龙 立，张艺欣，贺金川，董立国

(1. 西安建筑科技大学土木工程学院，西安 710055；2. 西安建筑科技大学结构工程与抗震教育部重点实验室，西安 710055；3. 西安建筑科技大学建筑设计研究院，西安 710055)

我国较多沿海城市处于高抗震设防烈度区域，常年面临地震灾害的威胁。同时，近海RC 框架结构由于长期受氯离子侵蚀影响，混凝土中钢筋锈蚀严重，引发钢筋截面削弱与力学性能劣化、混凝土保护层开裂与脱落、钢筋与混凝土之间粘结性能退化等，且随着服役期的增长上述退化程度日益加重，导致在役RC 框架结构抗震性能呈时变退化特性，加剧了近海RC 框架结构的地震灾害风险。

近年来，国内外学者在RC 框架结构抗震性能方面研究成果诸多，但在氯离子侵蚀下混凝土耐久性和结构抗震性能交叉领域的研究相对较少，如金伟良、郑山锁、贡金鑫、蔡立伦等[1-4]通过人工加速腐蚀试验方法模拟氯离子侵蚀环境，对锈蚀RC 框架柱、梁及节点的力学与抗震性能进行了试验研究与数值分析，揭示了其随锈蚀程度的劣化规律。Coronelli 等[5]考虑氯离子侵蚀对纵筋非弹性屈曲和低周疲劳退化的影响，建立了锈蚀矩形钢筋混凝土柱时变抗震能力评估的非线性有限元分析方法。Zandi Hanjari 等[6]通过对点蚀和均匀锈蚀的RC 梁分别进行建模分析，提出了钢筋均匀锈蚀和点蚀引起的破坏模式和剩余承载能力变化的预测模型。Yalciner 等[7]考虑钢筋横截面积损失、混凝土强度降低和粘结滑移的影响对单自由度RC 框架进行IDA 分析，预测了RC 框架结构抗震性能水平随锈蚀程度的变化规律，但其评估结果的准确性受到材料力学性能时变退化模型可靠性的制约。Shimomura 等[8]在对锈蚀RC 连续梁进行数值与对比分析后建议，应对锈蚀整体结构而不仅是其中的某些构件进行建模分析，以便充分了解结构的整体性能。

由上述相关研究成果可知，目前针对氯离子侵蚀下不同服役期RC 结构抗震性能的研究大多集中于构件层次抗震性能的衰减规律，对于RC 整体结构结构抗震性能的研究相对较少，难以揭示结构抗震能力随服役期的劣化规律，从而影响了氯离子侵蚀环境下在役钢筋混凝土结构抗震性能评估的准确性。鉴于此，本文提出氯离子侵蚀环境下不同服役期RC 整体结构的抗震性能研究，考虑服役期对材料力学性能的影响，分别对不同服役期、不同层数的RC 框架结构进行了静力与动力弹塑性分析，并分析了其承载与变形能力和屈服、倒塌PGA 随服役期退化规律和层间位移角变化规律，所得结果为既有RC 框架结构全寿命周期内的抗震性能评价与分析提供理论支撑。

1 钢筋剩余直径预测模型

氯离子侵蚀下钢筋锈蚀可分为去钝化阶段、发展阶段和锈胀开裂阶段，即：1) 氯离子不断渗透扩散到钢筋表面，其浓度累积达到钢筋脱钝阈值后，钢筋开始发生锈蚀；2) 在腐蚀电池作用和氯离子的去极化、导电作用下，钢筋锈蚀速度加快；3) 锈蚀产物累积，产生的锈胀力大于混凝土抗拉强度，保护层开裂。因此，为确定钢筋在某一服役期下的锈蚀程度，需先确定钢筋起锈时间，然后建立钢筋锈蚀后锈蚀程度与时间的关系模型。

1.1 钢筋去钝化阶段

氯离子在混凝土中传输机理复杂，扩散被认为其主要传输方式[9]，通过Fick 第二定律可以将氯离子的扩散浓度、扩散系数与扩散时间联系起来，且与实测结果吻合较好。不同深度处氯离子时变浓度按下式计算[10]：

式中：Cs为混凝土表面氯离子浓度；erf(·)为误差函数；t 为结构服役期；x 为距混凝土表面的深度；D 为扩散系数，其是时间的函数，Dura Crete[11]考虑测量参数的不确定性和环境条件的不同，提出扩散系数的经时模型如式(2)所示：

式中：D0为经验扩散系数；t0为暴露时间；ke为环境修正参数；kt为考虑D0测量方法差异的修正参数；kc为考虑养护条件差异的修正参数；n 为服役期因子。

当氯离子扩散Tcorr时间后，氯离子侵蚀深度达到混凝土保护层厚度dc，且浓度达到钢筋脱钝临界氯离子浓度Ccr时，钢筋开始发生锈蚀，即：

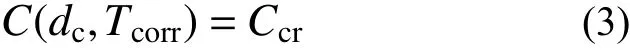
结合式(1)～式(3)，并考虑模型的不确定性，可得氯离子作用下钢筋锈蚀开始时间的概率模型如下：

式中：Tcorr为钢筋锈蚀开始时间；X1为模型不确定参数；dc为混凝土保护层厚度；Ccr为临界氯离子浓度，为氯离子含量占胶凝材料的质量百分比；Cs为表面的氯离子浓度，计算公式为Cs=Acs·(w/b)+εcs，式中 Acs、 εcs为模型参数，w/b 为水胶比；其余符号同前。

1.2 钢筋锈蚀发展阶段

锈蚀开始后，钢筋剩余直径取决于锈蚀速度，而钢筋锈蚀速度与混凝土保护层厚度、水胶比、配筋率等诸多影响因素有关。因缺乏钢筋锈蚀速度的现场实测数据，本文采用文献[12]提出的钢筋剩余直径预测模型，如式(5)所示：

式中： dbi为在t=0 时钢筋初始直径；w/c 为水胶比；dc为混凝土保护层厚度；t 为结构的服役期。

2 材料力学性能退化模型

2.1 保护层混凝土开裂软化

混凝土横向平均拉应变会引起纵向微裂缝的产生，从而导致受压混凝土强度的降低，即保护层混凝土强度衰减程度取决于横向平均拉应变的大小，故保护层混凝土开裂后抗压强度计算公式[13]为：

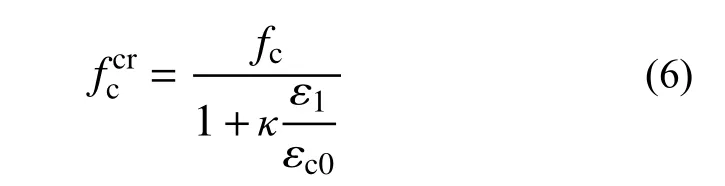
式中： fccr/MPa 为开裂混凝土的抗压强度； εc0为完好混凝土峰值压应力 fc对应的应变；κ 是与钢筋粗糙程度和直径有关的系数，对于一般直径钢筋取0.1[14]； ε1为开裂混凝土中沿裂缝宽度方向的平均拉应变，即横向平均拉应变，按式(7)计算：

式中：b0为未锈蚀构件截面宽度；nbars为受压区钢筋数量；wcr为某一锈蚀深度x 时混凝土锈胀裂缝宽度，可通过式(8)计算[15]：

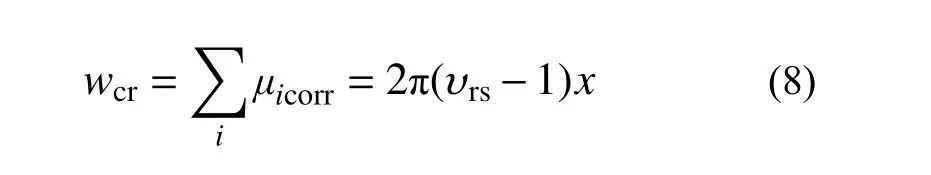
式中：υrs为 锈蚀膨胀系数，取值为2。

2.2 锈蚀钢筋力学性能退化

张伟平等[16]通过对实际工程锈蚀钢筋应力应变关系研究发现：随着锈蚀程度的加剧，钢筋的屈服强度、极限强度和极限应变均逐渐退化，但弹性模量基本不改变。式(9)给出了钢筋屈服强度、极限强度和极限应变与锈蚀率的关系模型。

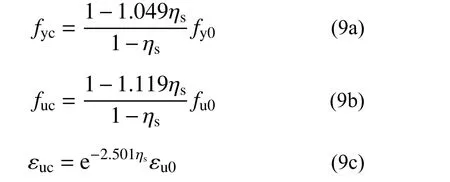
式中： fyc、 fuc分别为锈蚀钢筋的屈服强度、极限强度； fy0、 fu0分别为未锈蚀钢筋的屈服强度、极限强度； εuc、 εu0分别为锈蚀钢筋和未锈蚀钢筋的极限应变；ηs为钢筋锈蚀率。

2.3 约束混凝土力学性能退化

箍筋的锈蚀将导致核心区混凝土约束强度比和极限压应变的降低。本文基于Mander 约束混凝土本构模型[17]和2.2 节所提模型，通过折减箍筋力学性能考虑锈蚀对约束混凝土影响。箍筋锈蚀后约束混凝土极限压应变 εcuc按下式计算：

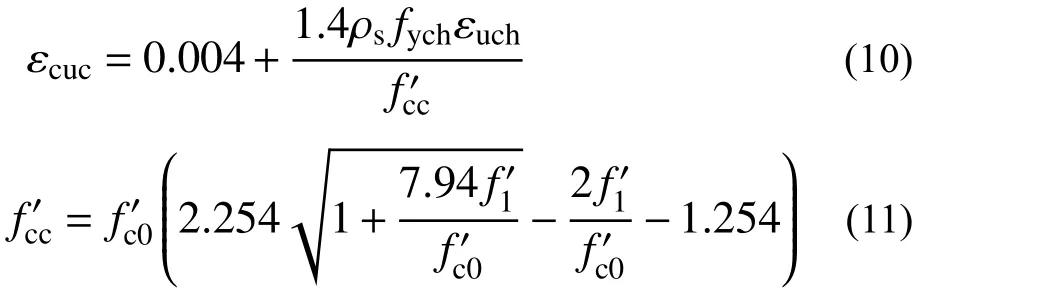
式中： fych为锈蚀箍筋的屈服强度，按式(9a)进行折减； εuch为锈蚀箍筋极限拉应变，按式(9c)进行折减； ρs为箍筋的体积配箍率，其不因锈蚀影响而改变； fc′c为约束混凝土两轴等压的三轴强度；fc′0为非约束混凝土的抗压强度； f1′为有效侧向约束应力。

2.4 锈蚀框架梁柱塑性铰长度

文献[18]将塑性铰区的曲率分布简化梯形，并给出了与钢筋直径和钢筋屈服强度有关的塑性铰长度计算公式，其计算相对简便且具有一定精度。在此基础上，本文基于1.2 节钢筋剩余直径计算模型和2.2 节锈蚀钢筋力学性能退化模型，定义锈蚀后框架梁柱单元塑性铰区域长度如下：

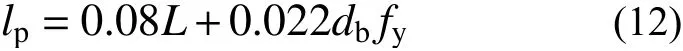
式中： db/mm 为钢筋锈蚀后剩余直径，按式(5)计算； fy/MPa 为纵筋锈蚀后的屈服强度，按式(9a)计算； L/mm 为框架梁跨度和柱高度。

2.5 模型验证

为验证上述建模方法的准确性和适用性，本文采用Mander 混凝土本构和Menegotto-Pinto 钢筋本构分别对文献[19 - 21]中的锈蚀RC 柱和整体RC框架试件进行拟静力加载模拟分析，所得模拟滞回曲线和试验滞回曲线对比如图1 所示。

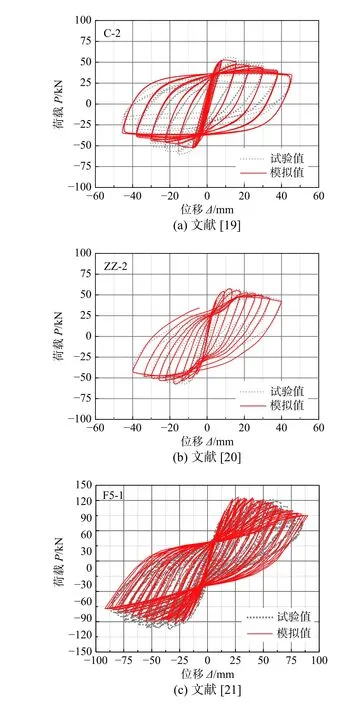
图1 滞回曲线模拟结果验证Fig. 1 Verification of the computational model

本文通过承载力误差Ef和累计耗能误差Ee评估模型的准确性，其计算方法分别如式(13)和式(14)所示。

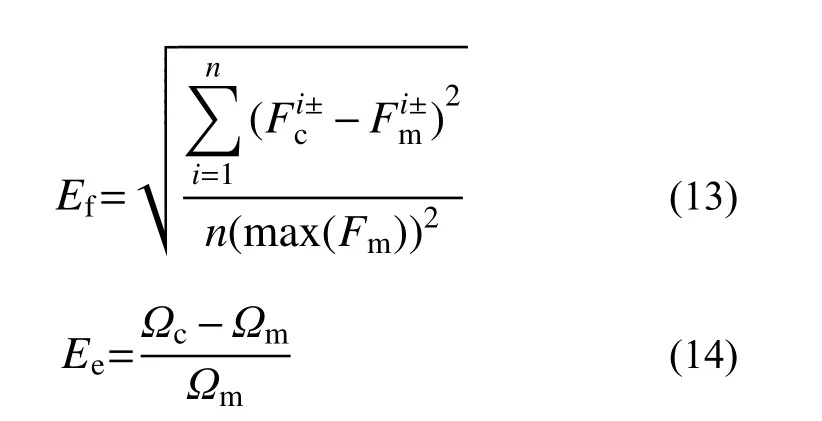
式中： Fmi±和 Fci±分别为滞回曲线第i 圈正反向峰值位移所对应的荷载试验值和模拟值；n 为滞回曲线正反向峰值位移点数； Ωm和 Ωc分别为试件累计耗能试验值和模拟值。锈蚀RC 柱和整体RC 框架模拟误差计算结果如表1 所示，从表中可以看出三次模拟结果承载力误差平均值为9.93%，累计耗能误差平均值为15.67%，说明本文所提建模方法具有一定准确性和适用性，可用于不同服役期RC 结构地震反应分析。

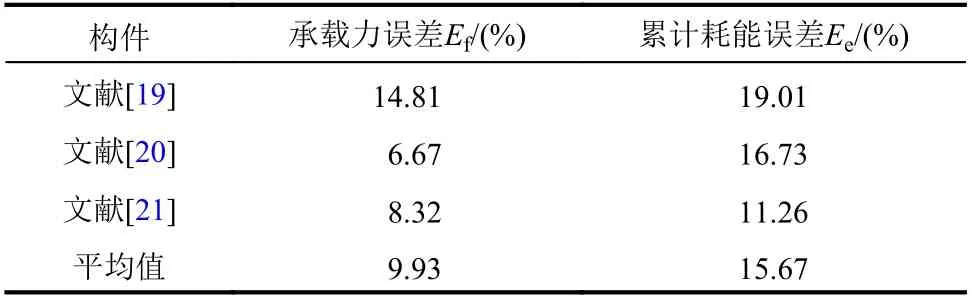
表1 模拟误差计算结果Table 1 Result of the error in computational model

3 算例分析

3.1 结构设计资料

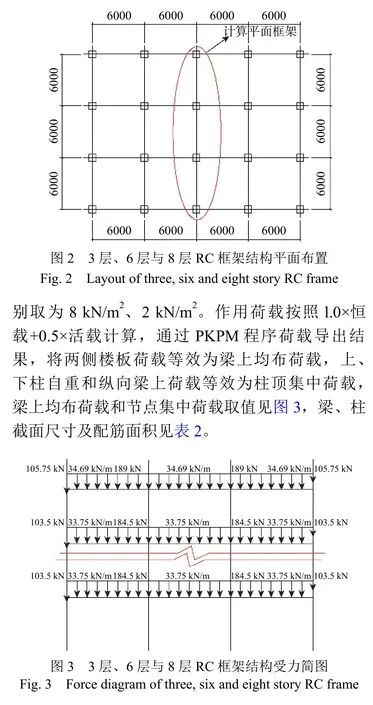
3.2 钢筋锈蚀程度计算

根据Dura Crete[11]规范建议，本算例中钢筋去钝化阶段氯离子扩散模型中参数取值如表3 所示。

根据式(4)计算箍筋、纵筋表面开始锈蚀临界时间 Tc均值分别为17.0 年和27.1 年。可发现箍筋先于纵筋发生锈蚀，分析其原因为：较于箍筋，纵筋拥有更厚的混凝土保护层，氯离子侵入到纵筋表面并达到临界氯离子浓度所需时间更长，故较晚发生锈蚀。

本文按结构处于理想最不利侵蚀条件考虑氯离子侵蚀对结构腐蚀程度的影响。基于式(5)和上述条件计算钢筋临界锈蚀时间，计算直径为20 mm和8 mm 的钢筋锈蚀率与服役期的关系模型，如图4 所示。从图4 中可看出，箍筋锈蚀率始终大于纵筋，且在服役70 年内，纵筋锈蚀率均小于10%。

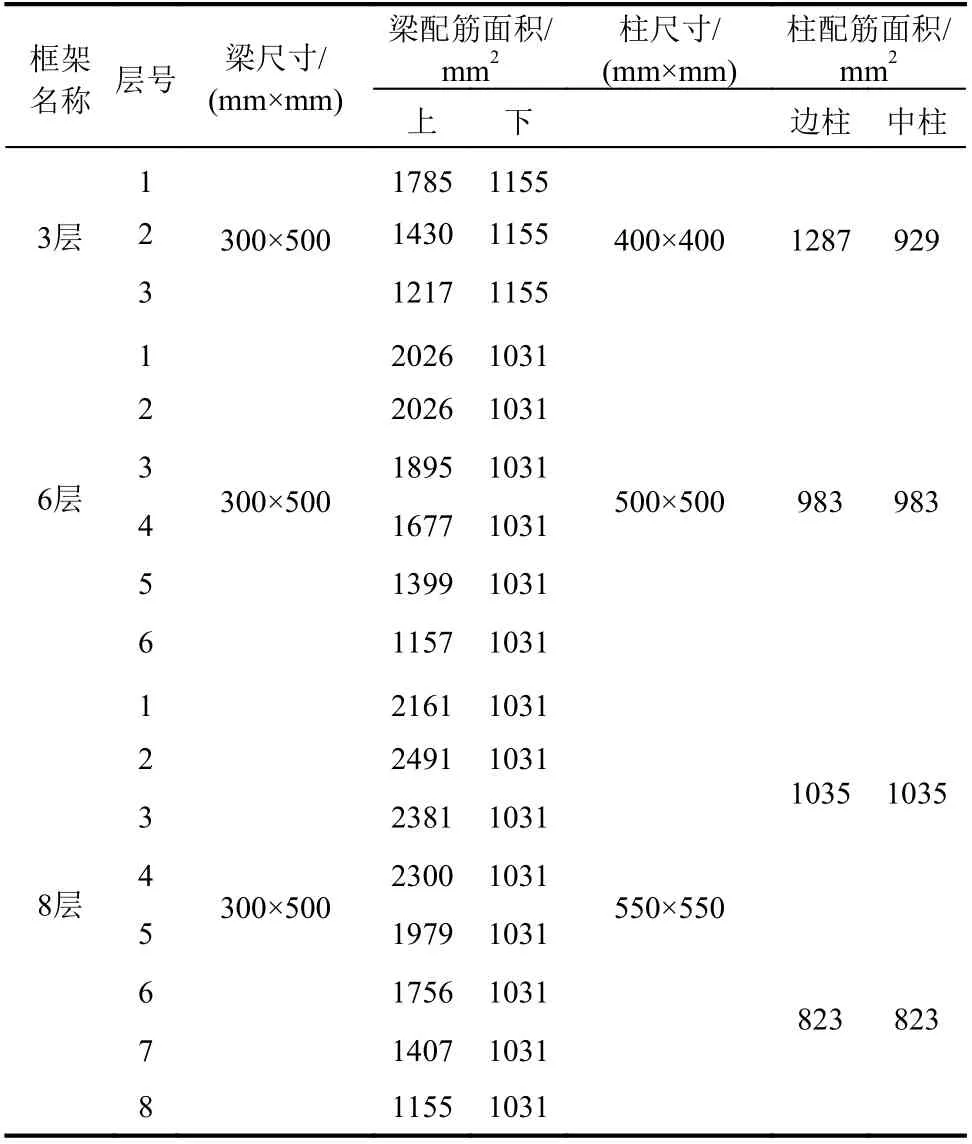
表2 RC 框架梁、柱尺寸及其配筋Table 2 Cross-sectional design of the RC frame columns and beams

注：3 层、6 层框架梁、柱箍筋为 8@100/200；8 层框架梁、柱箍筋为 8@80/150；箍筋均为四肢箍。文献[22]表明：对于锈蚀率10%以下的纵向受力钢筋，可以忽略锈蚀钢筋粘结强度的退化。故本算例按第2 节所提模型，计算开裂混凝土抗压强度和锈蚀钢筋截面、屈服与极限强度、极限拉应变的退化程度，以及箍筋锈蚀造成的核心区混凝土约束强度比和极限压应变的降低程度，并在纤维模型中予以考虑。

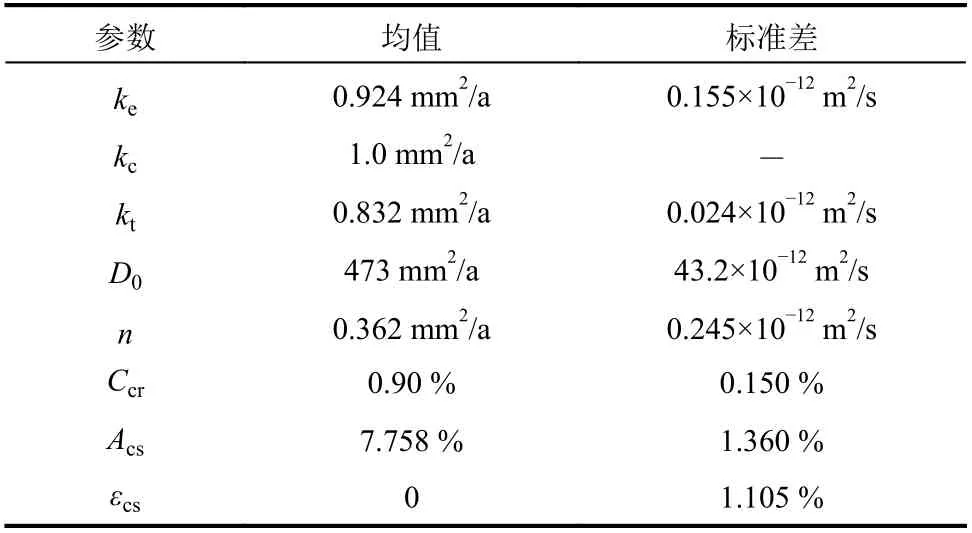
表3 氯离子扩散模型参数取值Table 3 Value of chloride ion diffusion model parameter

图4 纵筋( 20)和箍筋( 8)锈蚀率与服役期的关系Fig. 4 Relationship between corrosion rate of B20 longitudinal reinforcement and A8 stirrups and the service age

3.3 不同服役期RC 框架Pushover 分析

本文采用seimostruct 有限元模拟软件中基于位移的非线性框架单元，并选用Mander 混凝土本构和Menegotto-Pinto 钢筋本构，分别建立3 层、6 层与8 层RC 平面框架结构服役期为0 年、30 年、50 年和70 年的数值模型。RC 平面框架结构数值模型见图5。

图5 RC 平面框架结构数值模型Fig. 5 Numerical model of typical RC plane frame

采用倒三角加载模式进行Pushover 分析，得到不同层数的RC 不同服役期框架结构Pushover曲线如图6 所示。根据等能量法[23]确定结构的屈服位移，并将峰值荷载Pmax下降到0.85Pmax定义为结构破坏点，位移延性系数定义为破坏点位移与屈服位移的比值[24]。不同层数结构Pushover 曲线特征点位移、荷载及其退化率结果详见表4。从图6 和表4 可知：随服役期的增加，3 层、6 层与8 层结构弹性刚度基本保持不变，而结构承载力、特征点位移、位移延性、软化段刚度均逐渐减小，抗震性能不断降低。其具体表现为：结构破坏位移对服役期的敏感性高，退化最为显著，最大退化率可达25.57%；服役70 年后，3 层、6 层与8 层结构峰值承载力分别下降了10.9%、12.6%、11.6%，位移延性系数降低了11.2%、22.7%、15.2%。可以发现，6 层RC 框架抗震性能退化程度最为严重，8 层次之，3 层最轻，分析其原因为：结构层数越多，受氯离子侵蚀影响范围越广，钢筋锈胀作用导致的抗震性能降低累计程度亦越大，故相同服役期和抗震等级下，3 层RC 框架结构抗震性能衰减程度小于6 层框架结构。此外，8 层、6 层框架结构抗震等级分别为二级和三级，8 层抗震等级较高，遭受氯离子侵蚀影响时其抗震能力富余度较大，且抗震等级对抗震性能退化程度的影响较结构层数大，故相同服役期下其抗震能力退化程度较6 层框架结构轻。综上可以得出，相同抗震等级下，随着框架结构层数的增加，结构承载能力和变形能力退化程度呈增大趋势，故在不同服役期RC 框架结构抗震性能时变劣化问题分析中，应计入结构高度的影响。

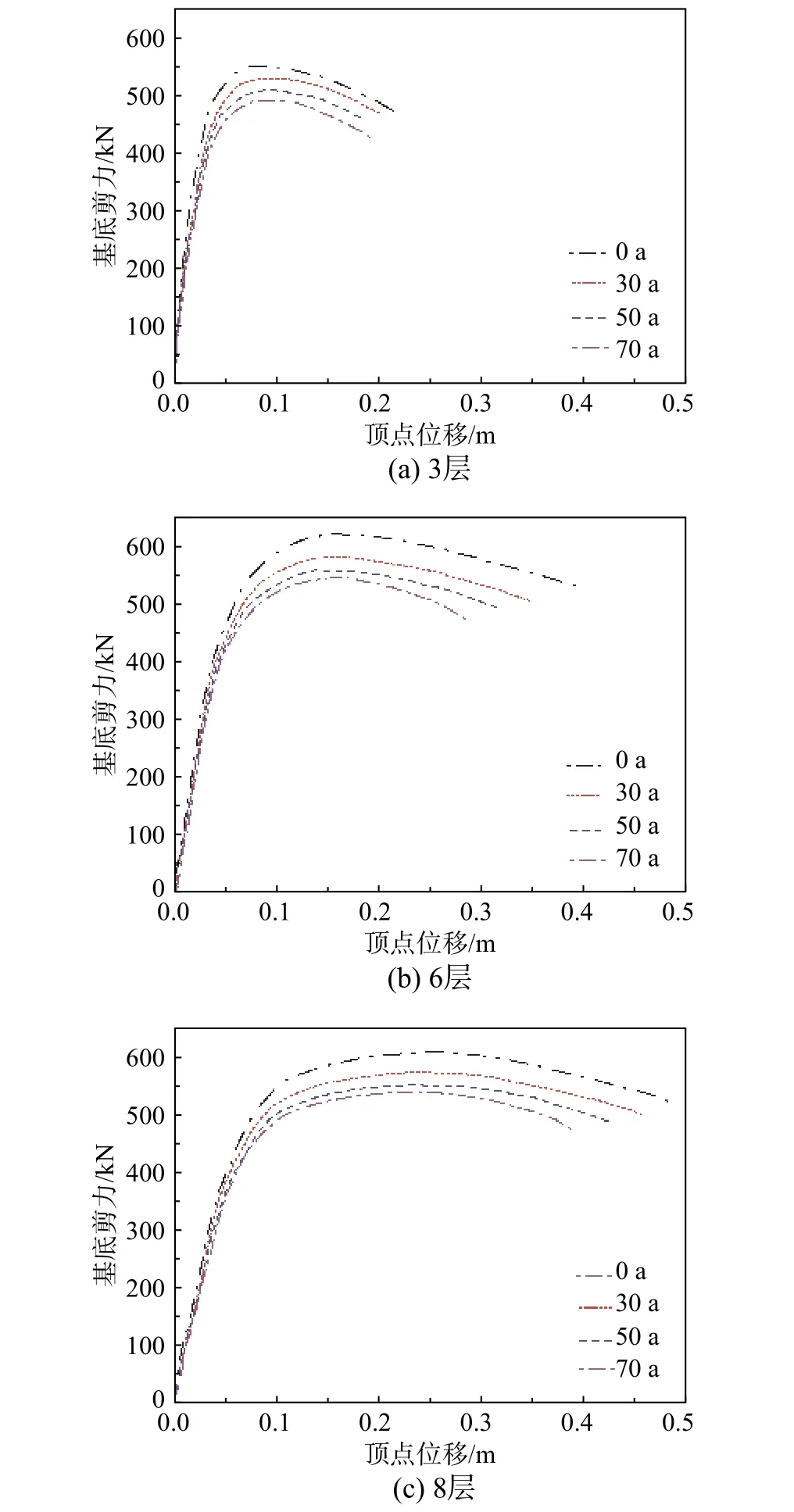
图6 不同服役期RC 框架结构Pushover 曲线Fig. 6 Pushover curve of multi-age RC frame

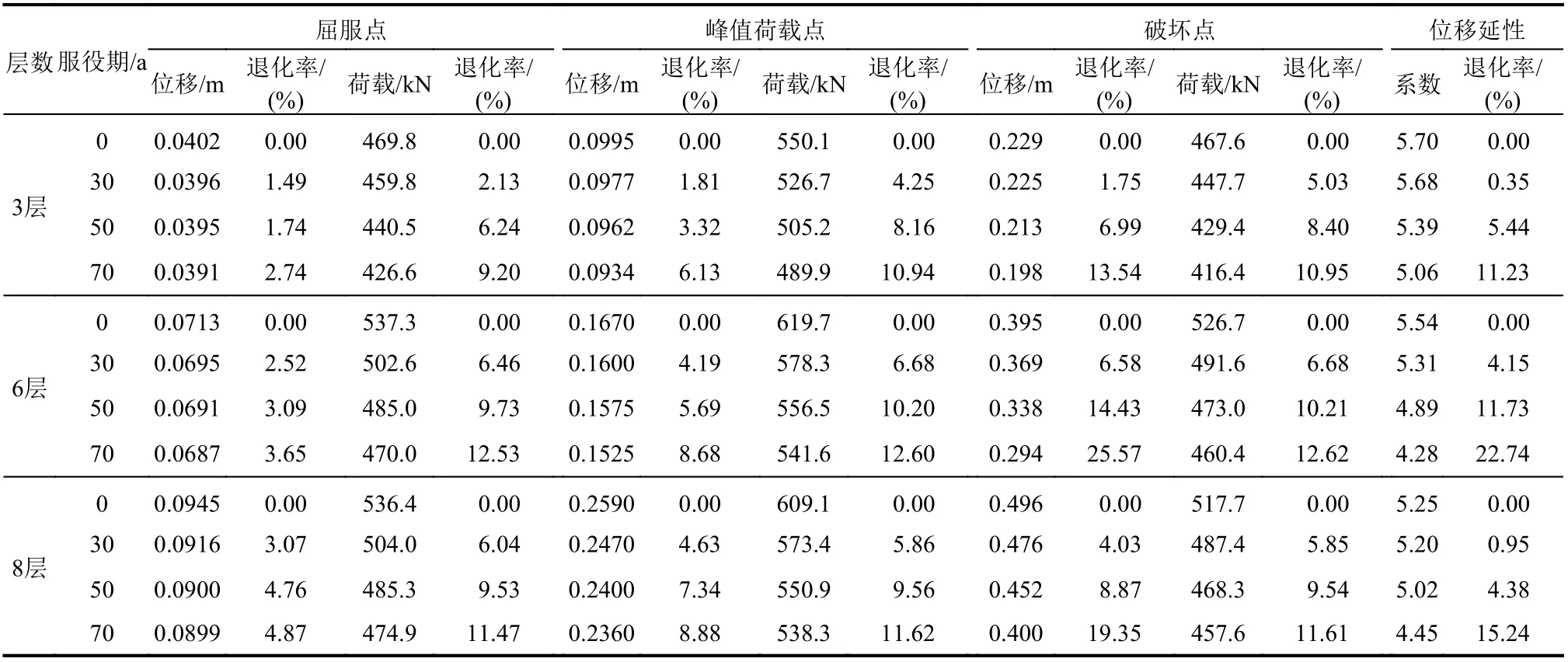
表4 3 层、6 层及8 层RC 框架Pushover 曲线特征点位移、荷载及其退化率Table 4 Feature point displacement and load of Pushover curve and its degradation rate of three, six and eight story RC frame

3.4 不同服役期RC 框架屈服和倒塌PGA

将RC 框架结构Pushover 曲线和设计反应谱转化为Sa-Sd谱曲线(ADRS 格式)，采用ATC40 中的能力谱法[25]，通过变化设计反应谱的PGA 使得结构性能点分别位于Pushover 曲线的屈服点和倒塌点，进而相应得到结构的屈服PGA(Ay)和倒塌PGA(Ac)，计算示意如图7 所示，图中Sy、Sc分别为结构屈服状态和倒塌状态下第一周期谱加速度，Sdy、Sdc分别为结构屈服状态和倒塌状态下第一周期谱位移。

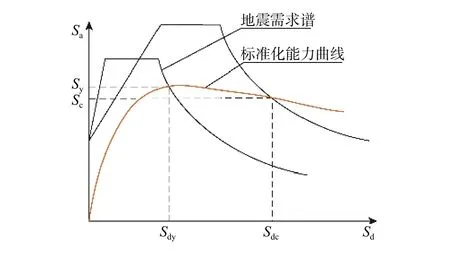
图7 结构屈服和倒塌PGA 的计算简图Fig. 7 Computational sketch of structural yield PGA and collapse PGA

以3 层RC 框架为例，按上述方法计算屈服PGA和倒塌PGA，并分别与8 度设防和罕遇烈度下对应的PGA 比较，结果见表5，3 层框架倒塌和屈服PGA 随服役期变化曲线如图8 所示。从表4和图8 中可得，当3 层RC 框架结构服役55 年后，不再满足大震不倒的设防标准，服役60 年后，不再满足中震可修的设防标准，且屈服PGA每10 年平均退化率0.95%，倒塌PGA 每10 年平均退化率为1.08%，可见结构的倒塌PGA 对服役期更为敏感。6 层和8 层框架的屈服和倒塌PGA随服役期退化的规律与3 层类似，限于篇幅不再予以叙述。

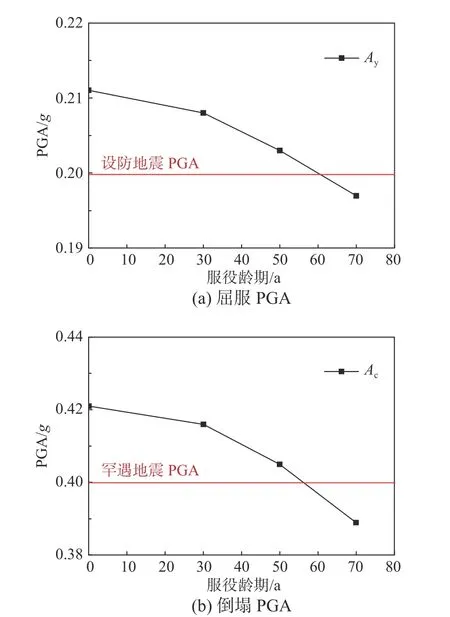
图8 3 层RC 框架屈服和倒塌PGA 随服役期变化曲线Fig. 8 Relationship curve between the PGA of the yield and collapse point and the service age of the three-story RC frame

表5 不同服役期RC 框架屈服和倒塌PGATable 5 Yield PGA and collapse PGA of multi-age RC frame

3.5 六层框架动力弹塑性时程分析

参照我国《建筑抗震设计规范》GB50011―2010 中有关规定，选择El-Centro 波、Taft 波两条天然波和一条人工波-兰州波作为输入地震波，继而对三条地震波进行反应谱分析(阻尼为0.05)，并将三条波的平均地震影响系数曲线与规范反应谱进行对比，其结果如图9 所示。可以看出三条波的平均反应谱曲线能与规范反应谱拟合较好，且底部剪力分析结果满足规范相应要求，可用于合理评估结构在地震作用下的响应。

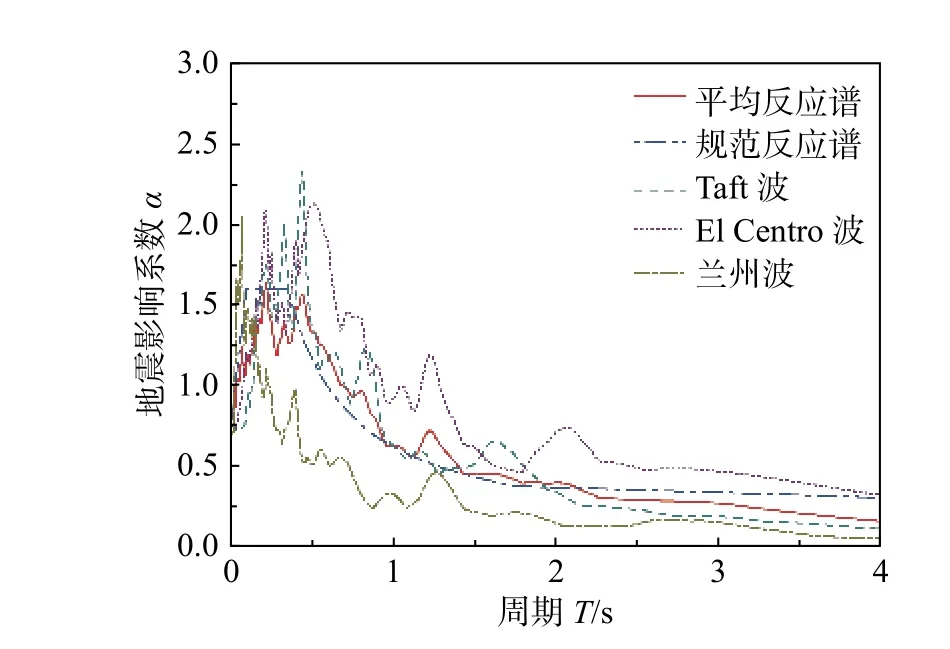
图9 三条地震波反应谱与规范设计反应谱Fig. 9 Three seismic wave response spectra and design response spectra

选取6 层不同服役期RC 框架结构为代表进行上述三条时程曲线的动力弹塑性时程分析，对3 条地震波下各楼层最大层间位移角取平均值，得到不同服役期RC 结构最大层间位移角平均值随楼层分布如图10 所示。从图10 可以看出，随着服役期的增长，设防地震和罕遇地震作用下各层层间位移角均不断增大。具体表现为：较于初始服役结构，结构服役30 年、50 年、70 年后，设防地震作用下最大层间位移角分别增加1.7%、2.9%和6.1%，罕遇地震作用下最大层间位移角分别增加5.1%、9.8%和14.4%，可见结构在罕遇地震作用下层间位移反应受服役期影响较设防地震作用更为明显。

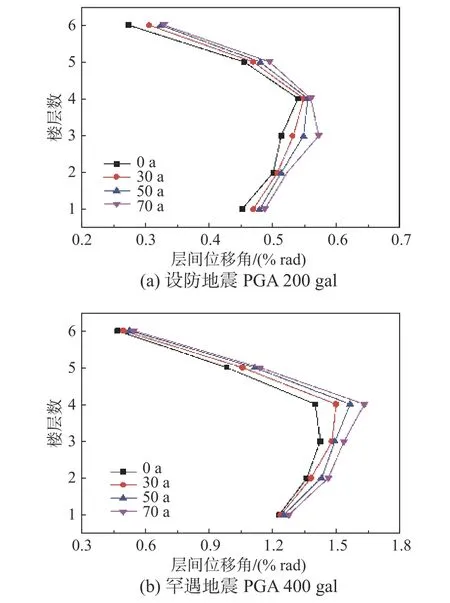
图10 最大层间位移角随楼层分布曲线Fig. 10 Distribution curve of the interstory drift ratio of multi-age RC frame Different

4 结论

本文考虑RC 框架结构钢筋截面削弱、保护层混凝土开裂软化、箍筋约束核心区混凝土能力减弱等模拟氯离子经时侵蚀的影响，预测了不同服役期下材料的力学性能退化规律，进而对服役期为0 年、30 年、50 年、70 年的3 层、6 层与8 层框架结构进行了静力与动力弹塑性分析，研究了氯离子侵蚀下不同服役期RC 框架结构抗震性能随服役期的劣化规律。所得主要结论如下：

(1) 基于钢筋锈蚀深度预测模型，提出了氯离子侵蚀环境下RC 不同服役期结构建模分析方法。与现有单一缩减纵筋直径的建模方法相比，考虑了钢筋锈胀导致的材料性能退化机理，使不同服役期RC 结构数值建模方法更为合理。

(2) 随着服役期的增加，RC 框架结构承载力、特征点位移、位移延性、下降段刚度等抗震性能指标均逐渐减小。较于层数较低RC 框架，服役期对高层RC 框架的抗震性能劣化影响更为严重。

(3) 随着服役期的增加，RC 框架结构的屈服PGA 和倒塌PGA 不断降低，屈服PGA 每10 年平均退化率0.95%，倒塌PGA 每10 年平均退化率为1.08%。较于屈服PGA，结构倒塌PGA 对服役期更为敏感。

(4) 随着服役期的增加，在相同地震作用下RC 框架结构最大层间位移角不断增大，且结构在罕遇地震作用下层间位移角受服役期影响较设防地震作用下更为明显。