带消能连梁的矩形空心双柱式高墩抗震性能试验研究
2020-07-20王天琦孙利民
王 源,王天琦,孙利民,谢 文
(1. 宁波大学土木与环境工程学院,宁波 315211;2. 同济大学土木工程防灾国家重点实验室,上海 200092)
桥梁结构抗震设计的一个重要发展趋势是正从单纯的抗震、减震设计向功能可恢复设计转变[1]。桥墩作为桥梁的主要承重构件,其地震失效将引起桥梁震后功能的完全丧失[2],因此,桥墩对桥梁的整体抗震性能起至关重要作用。已有震害表明:钢筋混凝土桥墩在遭受强震后,会发生较大的残余位移[3],无法修复或者修复代价过高而被拆除,造成巨大的经济损失,阻碍震后城市交通和人们生产生活的快速恢复。
因此,有学者将结构震后功能可恢复设计理念引入双柱式桥墩抗震设计及加固[4]。随后,带消能构件双柱式桥墩的研究取得了长足发展,如El-Bahey 等[5-6]研究了防屈曲约束支撑(简称“BRBs”)和剪切板对双柱式桥墩抗震性能的影响,并建立了理论分析模型;谢文等[7]和孙利民等[8]研究了带BRBs 或剪切连梁的双柱式桥墩抗震性能及其在大跨度斜拉桥地震损伤控制中的应用;孙治国等[9]研究表明:BRBs 可有效减小排架墩的地震损伤;谢文等[10]建立了基于结构“保险丝”概念的双柱式高墩地震损伤控制设计方法,通过算例验证了该方法的可行性和有效性;刘晓刚等[11]研究了一种由消能构件和钢管混凝土组成的组合墩柱,表明墩柱具有很强的耗能能力、延性和变形能力;石岩等[12]建立了基于位移的BRBs 排架墩抗震设计方法,通过实例验证了其可行性;董慧慧等[13]研究了自复位耗能支撑应用于双柱式桥墩中的可行性和有效性,表明自复位耗能支撑可减小甚至消除双柱式桥墩的残余位移;徐秀丽等[14]研究了一种由混凝土角柱、装配式钢连梁和混凝土薄壁板组成的自耗能高墩体系,表明自耗能高墩除具有震后修复便利外,其耗能能力、承载能力和延性变形能力均优于传统薄壁墩;Dong 等[15]试验研究了BRBs 和自复位BRBs对双柱式桥墩损伤模式、残余变形和耗能能力等性能的影响。目前,利用消能构件来提升双柱式桥墩抗震性能的相关研究较多[16-21],而在双柱式高墩中的研究相对较少。
本文设计了一种带消能连梁的矩形空心双柱式高墩,采用拟静力试验研究带消能连梁的矩形空心双柱式高墩的强度、耗能、位移延性和墩柱曲率等抗震性能,然后与矩形空心双柱式高墩结果进行对比,验证带消能连梁的矩形空心双柱式高墩抗震性能的优越性。
1 试验模型
设计了2 个1/20 几何缩尺比的矩形空心双柱式高墩模型,即矩形空心双柱式高墩(简称“试件DCP”)和带消能连梁的矩形空心双柱式高墩(简称“试件DCP-E”),模型的其余关键相似常数如表1 所示,其中,矩形空心双柱式高墩作为对比方案,如图1 所示。双柱式高墩由基座、墩柱和盖梁组成,其缩尺高度为2825 mm,墩柱采用矩形空心钢筋混凝土截面,截面尺寸为260 mm×425 mm,壁厚为75 mm,墩柱中心间距为521 mm,纵筋配筋率和箍筋体积配筋率分别为1.95%和1.30%,满足我国公路桥梁抗震设计规范要求。试件DCP-E 的基座、墩柱和盖梁与试件DCP 完全相同,唯一不同的是:其墩柱之间安装了5 根低屈服消能连梁。
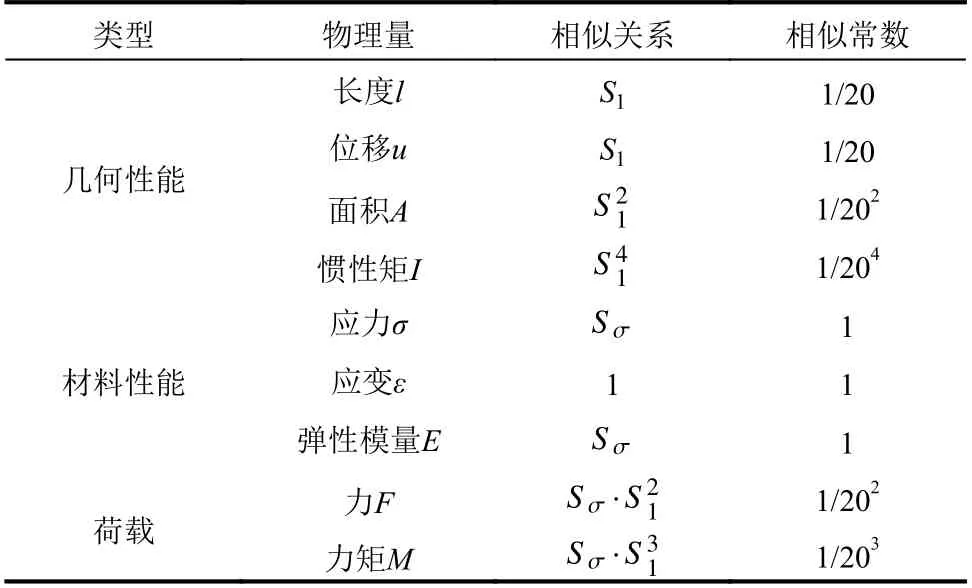
表1 试验模型与原模型相似比Table 1 Similarity ratios of test specimens to prototype model
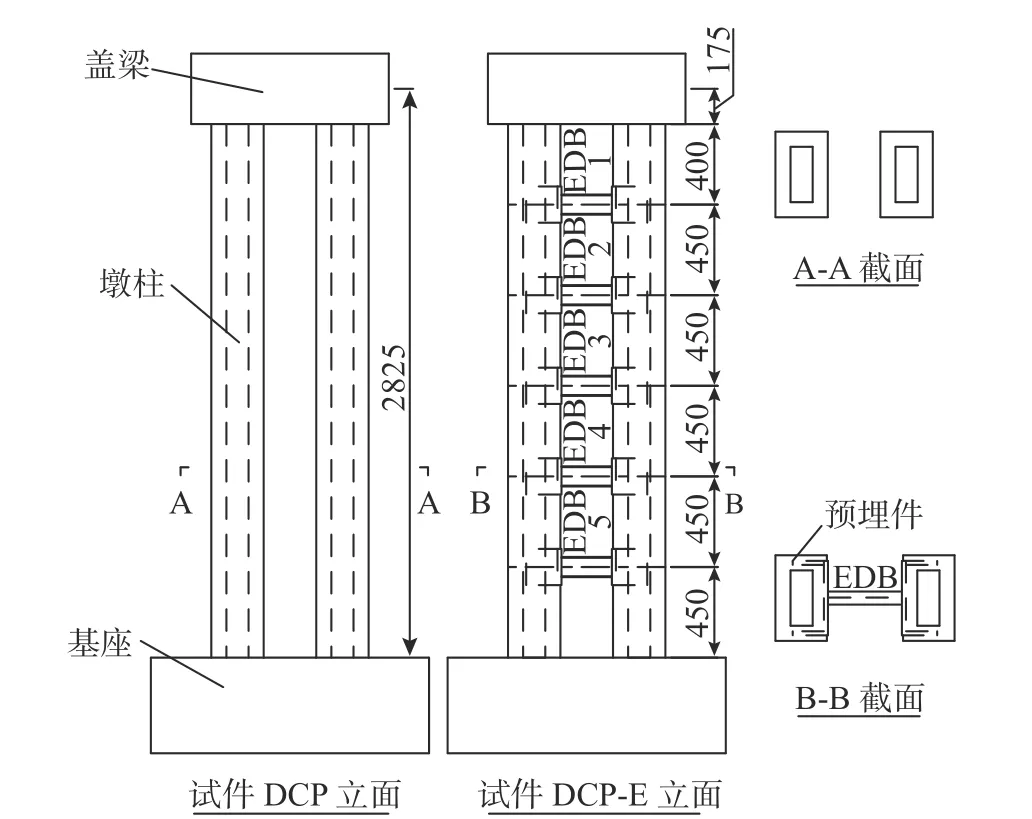
图1 试件的截面和立面 /mm Fig. 1 Cross section and elevations view of specimens
低屈服消能连梁(Energy Dissipation Beam, 简称“EDB”)采用Q235 工字钢制作,其几何尺寸如图2 所示。消能连梁为剪切型屈服构件,消能连梁与墩柱预埋件之间焊接,沿墩柱高度布置的竖向间距为400 mm~450 mm,如图1 所示。
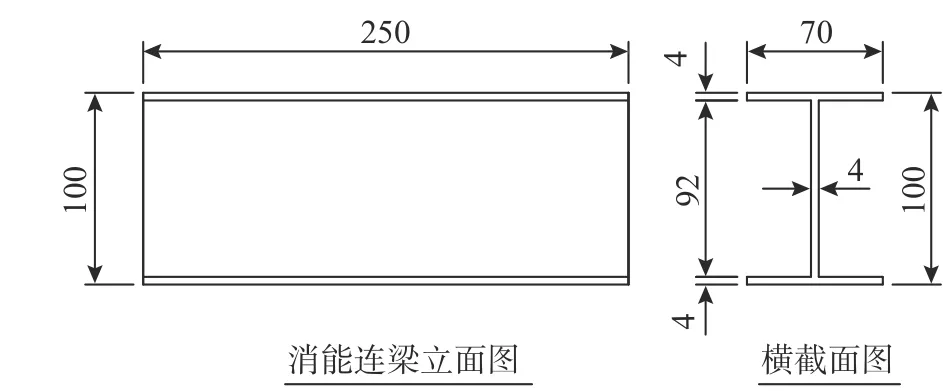
图2 消能连梁几何尺寸 /mm Fig. 2 Geometries of energy dissipation beam
2 试验方法
试验采用拟静力加载模式,MTS 伺服系统液压作动器与试件顶部连接施加往复水平荷载,作动器作用中心距试件基座顶部2.825 m,作动器的最大推力和拉力分别为500 kN 和280 kN,最大位移行程为±250 mm,试件基座用地脚螺栓固定于地槽。根据《公路抗震细则》第6.1.3 条规定规则桥梁中桥墩的轴压比应小于0.3[22],本次试验取轴压比为0.1[23],并采用预应力筋模拟该轴压比。试件加载方向如图3 所示。
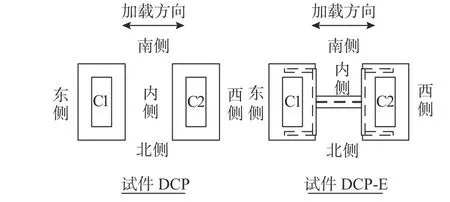
图3 试件加载方向Fig. 3 Schematic of specimens loading
加载机制采用等变幅混合位移控制,如图4所示。每级位移幅值循环加载3 次,首级位移幅值为5 mm,随后每级递增5 mm,直到加载至30 mm位移幅值,之后每级递增10 mm,直至纵筋断裂或峰值荷载下降至80%。作动器采样频率为1 Hz,且在每级位移的每次循环加载到位时持载5 min,保证混凝土裂缝充分开展,同时便于观察和记录试件破坏现象。
位移测量,墩柱底部、中部和顶部水平位移、基座水平滑移和竖向抬升位移;应变测量,墩柱塑性铰区的纵筋和箍筋、消能连梁的腹板和顶板,可通过应变判断钢筋和消能连梁是否屈服;曲率测量,墩底和墩顶等塑性铰区域曲率,采用接触式位移计测量两边相对位移,其布置示意如图5 所示,再根据式(1)计算其平均曲率。
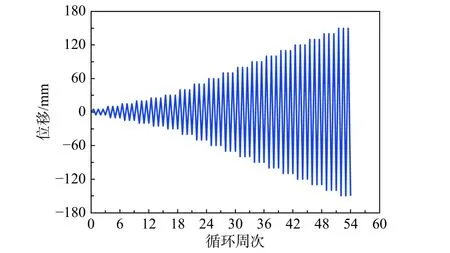
图4 加载方案Fig. 4 Loading protocol
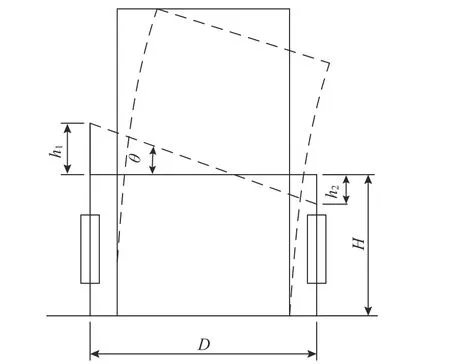
图5 平均曲率计算示意Fig. 5 Schematic of calculating average curvature
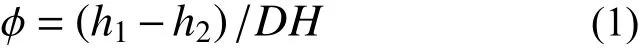
式中:h1、h2为布置在两侧的位移传感器的测量值;D 为试件截面长度;H 为测量高度。
消能连梁的平均剪切变形无法直接测量,可通过变形区域内矩形腹板对角线变化值间接得到。其测量原理和计算方法按式(2)计算,其中,矩形腹板对角线变化值通过腹板两侧位移传感器测得,如图6 所示。
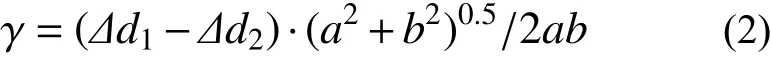
式(2)中: Δd1=-d1和 Δd2=-d2分别为矩形对角线长度变化值;a 和b 分别为矩形边长。
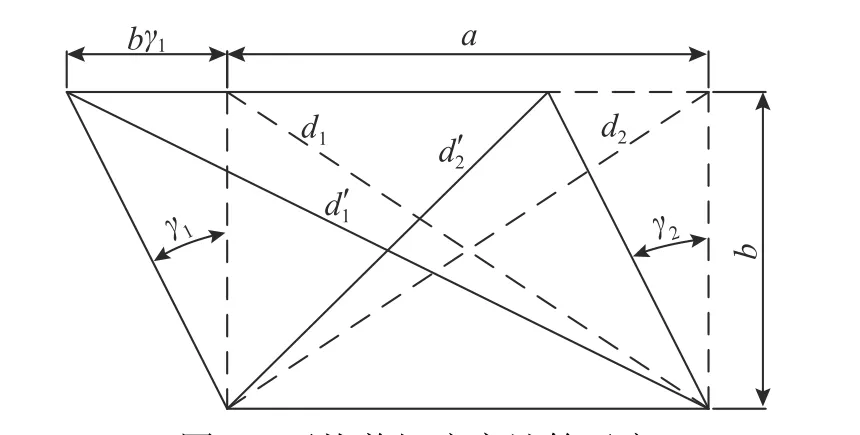
图6 平均剪切应变计算示意Fig. 6 Schematic of calculating average shear strain
3 试验结果分析
3.1 破坏过程及现象
加载过程中,试件墩底首先出现水平裂缝,且随位移等级增加,其裂缝开始向侧面延伸扩展,并在侧面出现斜裂缝。最终,试件的破坏模式均为典型的弯曲破坏,即在墩底形成塑性铰,且最终均达到承载能力极限状态。
3.1.1 试件DCP
加载位移为20 mm 时,试件DCP 的C1 柱东面(见图3)距墩底约50 cm 处首次出现3 条~4 条水平裂缝,如图7(a)所示,根据记录的钢筋应变,C1 柱和C2 柱北面柱脚处纵筋已开始屈服;加载位移增至25 mm 时,C1 柱东面水平短裂缝增多,部分原有裂缝延长,同时南北面距墩底约60 cm高度以内出现较多水平裂缝,墩底侧面大部分纵筋和墩顶少部分纵筋屈服;当加载位移为30 mm时,东西两侧水平裂缝贯通,见图7(b),东西两侧裂缝大量增加,新裂缝出现高度升至约100 cm,南北两侧首次出现斜裂缝;加载位移增至40 mm 时,墩柱侧面根部附近出现水平裂缝,且在棱角处与正面水平裂缝贯通,墩顶侧面部分钢筋发生屈服;当加载位移达60 mm 时,C1 柱东面柱脚处小块混凝土剥起,如图7(c)所示;加载位移为70 mm时,C1 柱东面靠近柱脚处一块高约5 cm 和长约10 cm 的混凝土块剥落。当加载位移达90 mm时,C1 柱东面墩底5 cm 范围以下混凝土全部剥落,如图7(d)所示,东北向柱脚10 cm 高度以下混凝土压碎剥落,棱角处一根箍筋裸露;当加载位移至130 mm 时,纵筋受拉断裂,如图7(e)所示;达到140 mm 时,C1 柱东面和C2 柱西面底部外侧纵筋基本全部受拉断裂,此时试件承载力迅速下降,试验加载中止。

图7 试件DCP 破坏形态Fig. 7 Failure modes of specimen DCP
3.1.2 试件DCP-E
当加载位移为10 mm 时,试件DCP-E 的C1柱东面(见图3)距墩底10 cm 处混凝土首次出现能完全闭合的裂缝;加载位移达20 mm 时,C2 柱西面距墩底约20 cm 处出现一条正面水平裂缝,如图8(a)所示,根据测量的消能连梁腹板相对位移和计算的理论屈服剪切变形可知,消能连梁EDB2和EDB4 已开始屈服,而钢筋未发生屈服;加载位移至25 mm 时,墩柱正面水平裂缝增多,新裂缝长度较长,出现位置上升至距墩底约60 cm处,消能连梁EDB1 和EDB3 也开始屈服;直到加载位移增加到40 mm 时,C1 柱和C2 柱墩底大部分纵筋和墩顶纵筋已发生屈服;当加载位移达到50 mm 时,C1 柱东面距离墩底1.1 m 的位置出现水平贯穿裂缝,C1 柱南侧首次出现斜裂缝,如图8(b)所示;当加载位移达60 mm 时,消能连梁EDB5 东侧预埋件下方少量混凝土剥落,如图8(c)所示;当加载位移为70 mm 时,C1 柱东面墩底水平贯穿裂缝宽度增大明显,柱脚出现竖向裂缝,有压碎迹象,消能连梁EDB5 西侧预埋件下方大块混凝土压碎剥落;加载位移增加到90 mm 时,C1 柱东面墩底5 cm 范围内表面混凝土基本全部剥落,如图8(d)所示,侧面出现大量长斜裂缝,C2 柱西北方向墩底大块混凝土压碎;当加载位移到达140 mm 时,C1 柱东面底部1 根纵筋和C2 柱西面底部3 根纵筋断裂,如图8(e)所示,此时墩柱承载能力迅速下降,加载中止。此外,消能连梁在整个试验过程中未出现破坏,只发生屈服,主要原因是预埋件提前松动导致消能连梁受力降低。

图8 试件DCP-E 破坏形态Fig. 8 Failure modes of specimen DCP-E
3.1.3 关键破坏现象对比
当加载位移为10 mm 时,试件DCP-E 出现了可完全闭合的裂缝,而试件DCP 未出现裂缝,其可能原因是消能连梁略增大了墩柱本身受力,导致试件DCP-E 的外层混凝土先出现可闭合的裂缝;当加载位移为20 mm 时,试件DCP 首次出现纵筋屈服,而试件DCP-E 部分消能连梁发生屈服,其钢筋直到加载至40 mm 时才发生屈服,其主要原因是消能连梁的屈服延缓了墩柱钢筋屈服,有效提高了墩柱的抗震性能,也表明消能连梁先于墩柱屈服耗能,可有效提高其耗能能力;当位移加载至130 mm 时,试件DCP 部分钢筋受拉断裂,而试件DCP-E 则在加载位移为140 mm时才出现纵筋断裂,因为消能连梁提高了双柱式桥墩的承载能力。
3.2 滞回曲线及骨架曲线
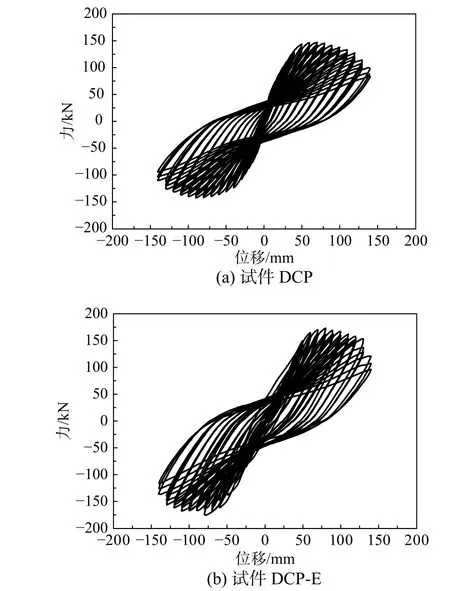
图9 试件滞回曲线Fig. 9 Hysteretic curves of specimens
段。对于试件DCP-E,消能连梁和纵向钢筋先后屈服,随着加载位移的增大,其滞回环面积进一步变大和饱满,呈弓形发展,其强度越来越强,且其滞回环面积和强度均大于试件DCP。如图10(b)~图10(f)所示,其主要原因是附加的消能连梁提高了双柱式桥墩的耗能能力和承载能力。因此,试件DCP-E 的滞回曲线相对更饱满,耗能能力更强。结果表明:消能连梁可有效提高双柱式高墩的耗能能力和承载能力等抗震性能。
通过连接试件DCP 和试件DCP-E 的滞回曲线上各级加载位移首次循环幅值对应的强度形成骨架曲线,如图11 所示。分析可知:当加载位移较小时,试件骨架曲线基本接近直线,处于弹性状态;当加载位移达到50 mm 后,带消能连梁的双
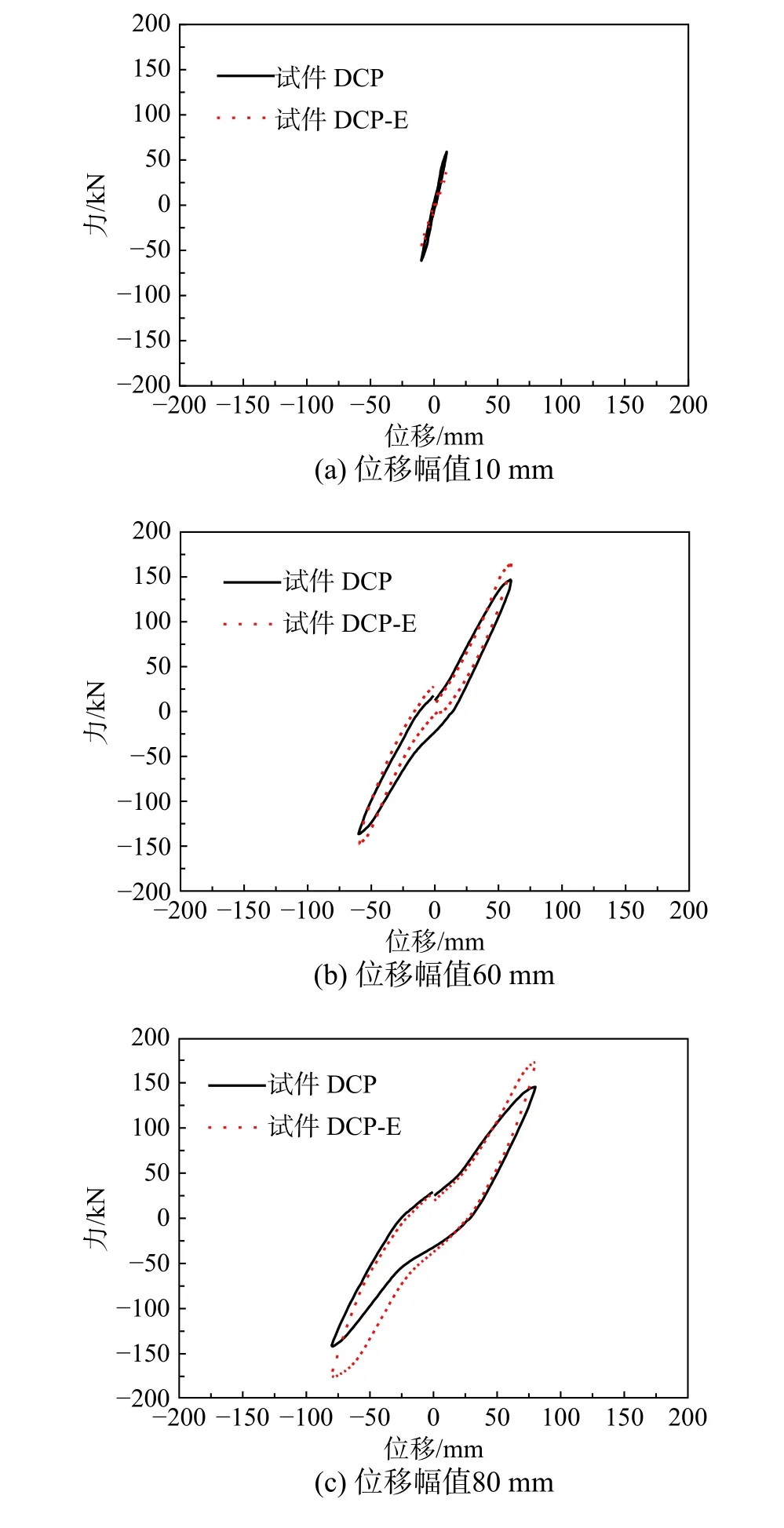
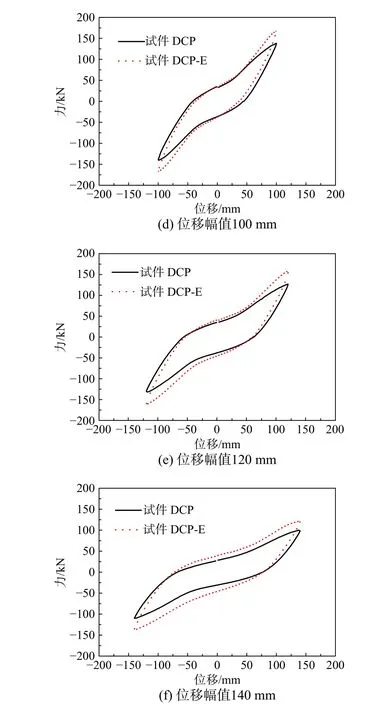
图10 典型位移幅值下两个试件的滞回环Fig. 10 Hysteretic loops of two specimens under the typical displacement amplitude
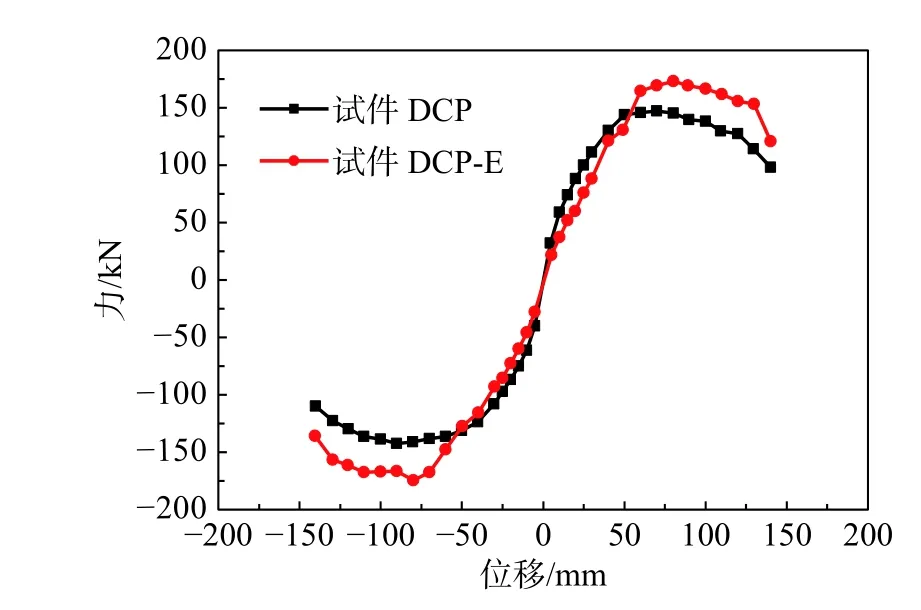
图11 试件的骨架曲线Fig. 11 Skeleton curves of specimens
图9 为试件DCP 和DCP-E 的滞回曲线,它是评价结构耗能能力的重要指标之一。由图9 可知,混凝土开裂前,试件的加载曲线与卸载曲线几乎重合,其滞回曲线呈直线;如图10(a)所示,表明其处于弹性阶段,混凝土开裂后,试件滞回环所包围的面积逐渐增大,开始进入滞回耗能阶柱式高墩承载能力继续增强,如试件DCP-E 的正负峰值强度分别为172.9 kN 和-174.7 kN,比试件DCP 的正负峰值强度分别高18.9%和22.5%;试件DCP-E 和试件DCP 的强度退化比较接近,如试件DCP-E 和试件DCP 极限位移对应的强度分别为相应峰值强度的77.9%和77.0%。表明消能连梁可明显提高双柱式高墩的峰值强度,而对其强度退化影响不明显。
3.3 累积滞回耗能
计算试件DCP 和试件DCP-E 的滞回环包围面积累积之和,得到其累积滞回耗能-位移关系,如图12 所示。分析可知,在试件强度退化前,试件DCP 和试件DCP-E 的累积滞回耗能随位移增大而增大。当加载位移小于80 mm 时,试件DCP 和试件DCP-E 的累积滞回耗能接近;而加载位移超过80 mm 后,试件DCP-E 和试件DCP 之间的累积滞回耗能显现差别,且前者增速更快,如试件DCPE 的耗能峰值为57.6×103kN·mm,比试件DCP 高27.7%;在极限位移140 mm 作用下,试件DCP-E 和试件DCP 的累积滞回耗能分别为55.7×103kN·mm和42.2×103kN·mm,前者比后者高32.0%。表明消能连梁可明显提高双柱式高墩的累积滞回耗能。
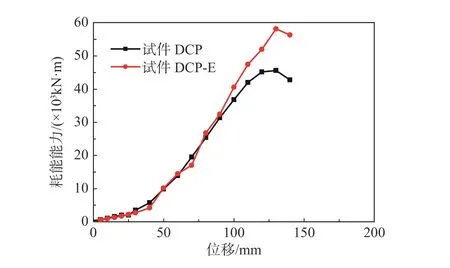
图12 试件的累积滞回耗能Fig. 12 Cumulative hysteretic energy dissipation curves of specimens
3.4 墩柱曲率和位移延性
墩柱曲率可有效评估结构的地震损伤。因此,图13 比较了试件DCP-E 和试件DCP 墩顶以及墩底的平均曲率,平均曲率为同级位移加载下三次循环之平均值。分析可知,绝大部分位移加载情况下,试件DCP-E 的墩底和墩顶曲率均小于试件DCP,如在约100 mm 位移作用下,试件DCP-E 的墩底和墩顶曲率比试件DCP 约低30%,表明在相同荷载作用下,带消能连梁的双柱式高墩相对来说更不易屈服和损伤,主要是由于消能连梁起附加耗能作用有效保护了墩柱主体结构。分析表明:消能连梁可有效降低墩柱的地震损伤,提高墩柱的抗震能力。

图13 C2 柱曲率-位移变化曲线Fig. 13 Relationship between curvature and displacement of C2 column of specimens
可用位移延性系数表示结构延性,通常最关心的是最大位移延性系数,其值为μ=Δu/Δy,其中Δu和Δy分别为极限位移和屈服位移,极限位移指试件强度下降至80%的峰值强度或者墩柱纵筋发生断裂时对应的位移;屈服位移指消能连梁或纵筋屈服时对应的位移。试件DCP 和试件DCP-E 的平均最大位移延性系数分别为6.2 和6.8,后者的位移延性系数比前者增大约10%。结果表明:消能连梁可提高双柱式高墩的位移延性能力。
3.5 耗能构件的变形能力
消能连梁的剪切变形由消能连梁的对角位移计算而得。图14 绘出了部分消能连梁的最大剪切变形(不计方向)与位移幅值的关系曲线,表2 列出了部分消能连梁的最大剪切变形和最大延性系数。随着加载位移的增大,各消能连梁的最大剪切变形基本随之增大;最大剪切变形延性系数为20 甚至更大,表明消能连梁可充分发挥耗能作用。值得说明的是,在位移幅值加载至120 mm时,消能连梁两端的预埋件明显松动,因此,消能连梁EDB1 后续加载对应的最大剪切变形和延性系数可能已失真。此外,靠近墩顶的消能连梁EDB2 和EDB1 的延性系数最大,高达20 以上,主要是因为墩顶之间的相对变形较大。
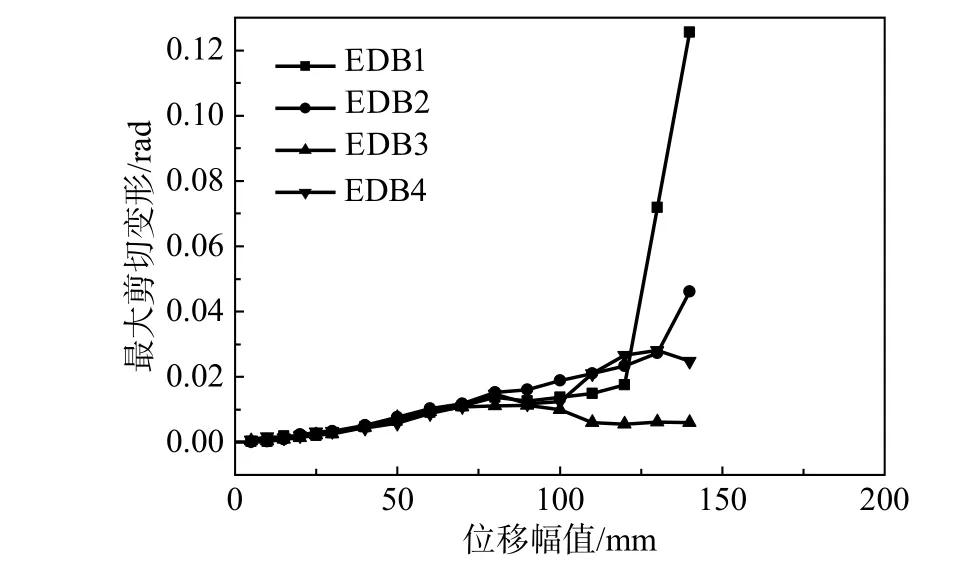
图14 消能连梁最大剪切变形随位移幅值的变化Fig. 14 Relationship between Maximum shear deformation and displacement of EDBs of DCP-E
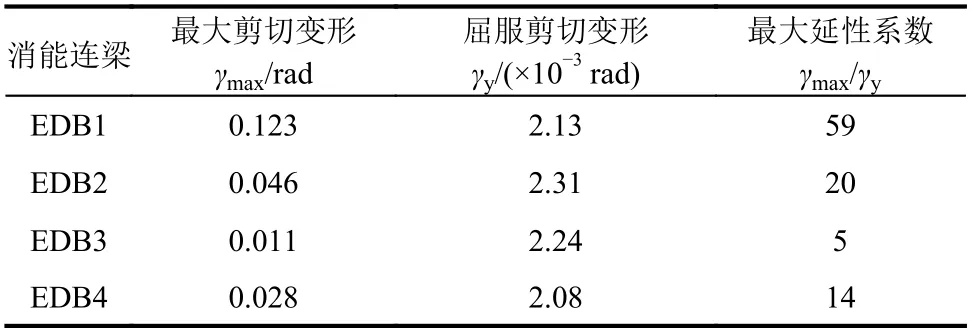
表2 消能连梁的延性Table 2 Ductility of EDBs
4 结论
开展了带消能连梁的矩形空心双柱式高墩和矩形空心双柱式高墩的拟静力试验研究,分析了试件的破坏形态及其过程,对比分析了两个试件的滞回曲线、骨架曲线、滞回耗能、墩柱曲率和延性位移等抗震性能,得到以下结论:
(1)带消能连梁的矩形空心双柱式高墩和矩形空心双柱式高墩均属于典型的弯曲破坏模式,即在墩底形成塑性铰。
(2)消能连梁可改善矩形空心双柱式高墩的抗震性能,使带消能连梁的矩形空心双柱式高墩具有更高的耗能能力和承载能力、更好的位移延性系数,因此,带消能连梁的矩形空心双柱式高墩具有更优越的抗震性能。
(3)消能连梁可有效降低墩柱曲率,且提高了墩柱的延性能力,在一定程度上保护了墩柱主体免遭地震损伤和提高墩柱的耗能能力。
(4)根据消能连梁的最大剪切变形和最大延性系数得出,消能连梁本身变形能力强,延性高。但需特别注意预埋构件的强度设计,防止其提前松动。
