异步LC-DS-CDMA信号DOA估计
2020-07-20李鑫凯张天骐梁先明
李鑫凯,张天骐,梁先明
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.中国西南电子技术研究所,四川 成都 610036)
0 引 言
在波达方向估计(direction of arrival,DOA)算法中[1,2],以经典的MUSIC[3,4]和ESPRIT[5,6]算法为代表。两种经典算法适用于窄带信号或低相关信号,而且信号数要小于阵元数。由于两种算法的一些不足,近几年来提出了一些改进的算法。文献[7]提出用协方差秩最小化的估计方法;文献[8]提出相关矩阵二次重构方法;文献[9]提出一种改进MUSIC算法,对局部信号空间进行谱峰搜索。对于宽带信号的波达方向估计,一般分为非相干宽带信号子空间ISM[10]和相干宽带信号子空间CSM[11]两种算法,ISM算法主要处理非相干信号的波达方向估计问题,而CSM可以处理相干信号,是把若干个窄带信号通过聚焦算法变换到同一频率下进行波达方向估计,因为需要聚焦,计算复杂。高阶累积量[12]算法能够抑制高斯白噪声的影响,是一种比较常用的方法。
本文研究了异步多用户长码直扩信号的波达方向估计,由于异步长码直扩信号是用一周期伪码调制多位信息码,导致信噪比很低,又因为异步多用户直扩信号是宽带信号,若直接用MUSIC算法估计波达方向,将导致估计结果不准确,而且目前关于异步多用户长码直扩信号的波达方向估计研究较少。针对上述问题,提出用相干信号子空间和高阶累积量算法对异步信号进行波达方向估计,分别仿真了异步周期和非周期信号在两种算法下成功概率和均方根误差。
1 阵列信号模型
1.1 直扩信号模型
异步多用户长码直扩信号的信号模型为
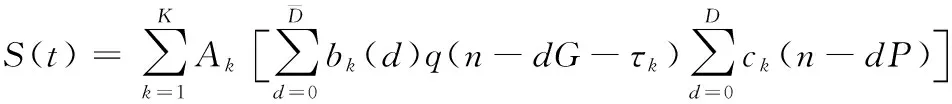
(1)
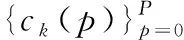
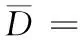
1.2 阵列信号模型
一般常用的阵列有圆阵,平面阵,直线阵等,本文采用一种计算简单的阵列信号模型,用M个等距排列的直线阵接收信号,阵元间距为l; 假设有K个远场异步LC-DS-CDMA 信号从不同的方向入射到阵列上,入射角为θ1,θ2,…θk, 假设噪声是均值为0,方差为σ2的高斯白噪声与信号是相互独立的,而且信号与信号间互不相关。选第一个阵元作为参考阵元,在t时刻时,第m个阵元上的接收数据为
X(t)=A(θ)S(t)+N(t)
(2)
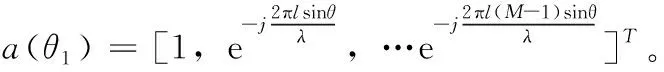
2 MUSIC算法
MUSIC算法是经典的窄带波达方向估计算法,通过构造空间谱,进行谱峰搜索估计入射方向。假设接收信号为X(t), 信号作自相关处理,得到协方差矩阵为
R=E[X(t)X(t)H]
(3)
其中,E表示期望,H表示矩阵的共轭转置。
由1.2节知,信号与噪声之间相互独立,故把式(2)带入式(3)中,得到
RX=E[X(t)X(t)H]=AE[SSH]AH+σ2IM
(4)
对RX进行特征分解得
(5)
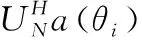
(6)
由于信号子空间与噪声子空间彼此正交,故当入射角等于θ时,PMUSIC(θ) 产生极大值,K个入射信号就会产生K个极大值,故出现K个峰值就对应K个信号。
3 波达方向估计算法
宽带信号的波达方向估计是把信号变到频域,然后分解成J个窄带,再用窄带算法估计波达方向。
把式(2)变换到频域,得采样信号为
X(f)=A(f,θ)S(f)+N(f)
(7)
假设观测时间为T0, 把观察时间T0分为P段,每段为TS=T0/P, 并对每个子带做j点傅里叶变换得到P段不相关的窄带频域分量,记为XP(fj),p=1,2,…P,j=1,2,…J。
3.1 CSM算法
CSM是估计宽带信号的波达方向的常用算法,通过聚焦矩阵将每个频率点的数据变换到参考频率,然后再用MUSIC算法进行估计。
构造聚焦矩阵T(fj), 满足
T(fj)A(fj)=A(f0),j=1,2…J
(8)
式中:f0为参考频率,把T(fj) 带入式(7)得
T(fj)X(fj)=T(fj)A(fj,θ)S(fj)+T(fj)N(fj)=
A(f0,θ)S(fj)+T(fj)N(fj),j=1,2,…,J
(9)
在本文中,选用旋转信号子空间变换算法(RSS)进行聚焦矩阵的构造,即
(10)
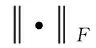
文献[13]提出了一种聚焦矩阵的形式
T(fj)=V(fj)UH(fj)
(11)
式中:U(fj) 和V(fj) 分别为A(fj)AH(f0) 经过奇异值分解的左奇异矢量和右奇异矢量。
聚焦变换之后阵列流型A(f0,θ) 不再随频率改变,把T(fj) 带入式(7),假设变换后的矩阵Y(fj), 即
Y(fj)=T(fj)X(fj),j=1,2,…J
(12)
对式(12)求协方差为
RY(fj)=E[Y(fj)YH(fj)]=A(f0,θ)RS(fj)AH(f0,θ)+
σ2T(fj)TH(fj)j=1,2,…J
(13)
由于分为J个窄带,则
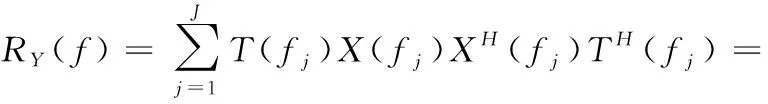
(14)
式中
RS(fj)=S(fj)SH(fj)
(15)
Rn(fj)=N(fj)NH(fj)
(16)
具体步骤为:
(1)先把信号分为P段,然后把每段均分成J个窄频段并进行傅里叶变换;
(2)由式(11)构造聚焦矩阵;
(3)经过变换得到式(12),再求其协方差矩阵,即式(14);
(4)最后用窄带方法求波达方向。
3.2 高阶累积量算法
高阶累积量能够估计抑制白噪声的影响,但是运算量比较大,本文采用四阶累积量,由下式表示
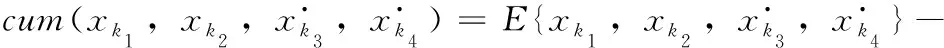
(17)
式中:k1,k2,k3,k4∈{1,2,…,M},M为阵元数。
本文采用聚焦后的矩阵式(12),在不同频率点构造四阶累积量矩阵CYj, 第 [(k1-1)M+k3] 行 [(k2-1)M+k4] 列的元素为
CYj=E{(Y⊗Y·)(Y⊗Y·)H}-
E{(Y⊗Y·)}E{(Y⊗Y·)H}-E{YYH}⊗E{(YYH)·}
(18)
式中:⊗表示Kronecker乘积,·表示共轭,H表示共轭转置。CYj共有M4个值,将M4个值放入M2×M2的矩阵RYj中,则式(18)为
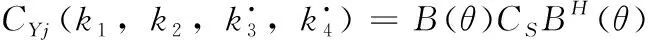
(19)
上式中
CS=E{(S⊗S·)(S⊗S·)H}-
E{(S⊗S·)}E{(S⊗S·)H}-E{SSH}⊗E{(SSH)·}
(20)
B(θ)=[b(θ1)b(θ2) …b(θk)]=
[a(θ1)⊗a·(θ1) …a(θk)⊗a·(θk)]
(21)
b(θ1)=a(θ1)⊗a·(θ1)
(22)
对式(19)进行加权平均得
(23)
对上式进行特征分解,由于有K个入射信号,故有K个较大特征值,M2-K个较小特征值,较小特征值组成的噪声子空间为En=[ek+1ek+2…eM2], 则空间谱为
(24)
具体步骤为:
(1)同3.1节步骤(1)和步骤(2)一样,得到Y(fj);
(2)由式(17)和式(18)求得CYj, 然后通过式(19)和式(23)求得四阶累量算法下的协方差矩阵;
(3)对式(23)进行特征分解,得到En;
(4)对式(24)进行谱峰搜索,得到异步信号的波达方向。
4 实验仿真及分析
通过matlab进行仿真,比较在不同阵元与不同信噪比下异步LC-DS-CDMA信号波达方向估计的成功概率和均方根误差。
以下实验都采用如下条件,实验中采用信源数k=3, 且相互独立,信号的入射角θ为-30°,0°,20°。本文选用均匀直线阵,阵元数为6,阵元间距为半波长,快拍数500,伪码周期63,信息码宽度21,信息码个数1000;扩频序列采用gold序列。噪声为高斯白噪声,且噪声与信号相互独立。
仿真实验一:取信噪比为-12 dB,仿真结果如图1、图2所示。
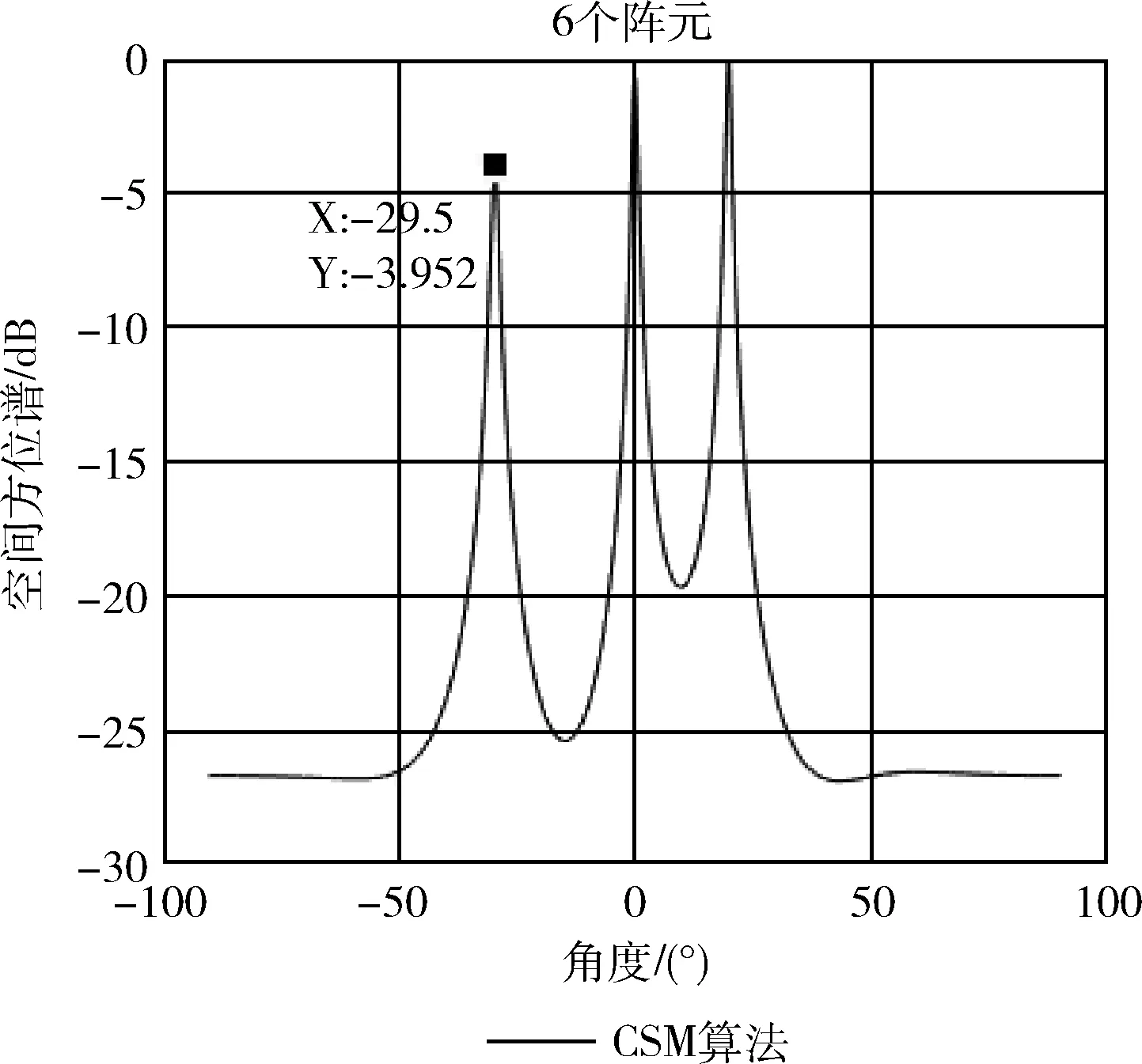
图1 异步PLC-DS-CDMA信号波达方向估计
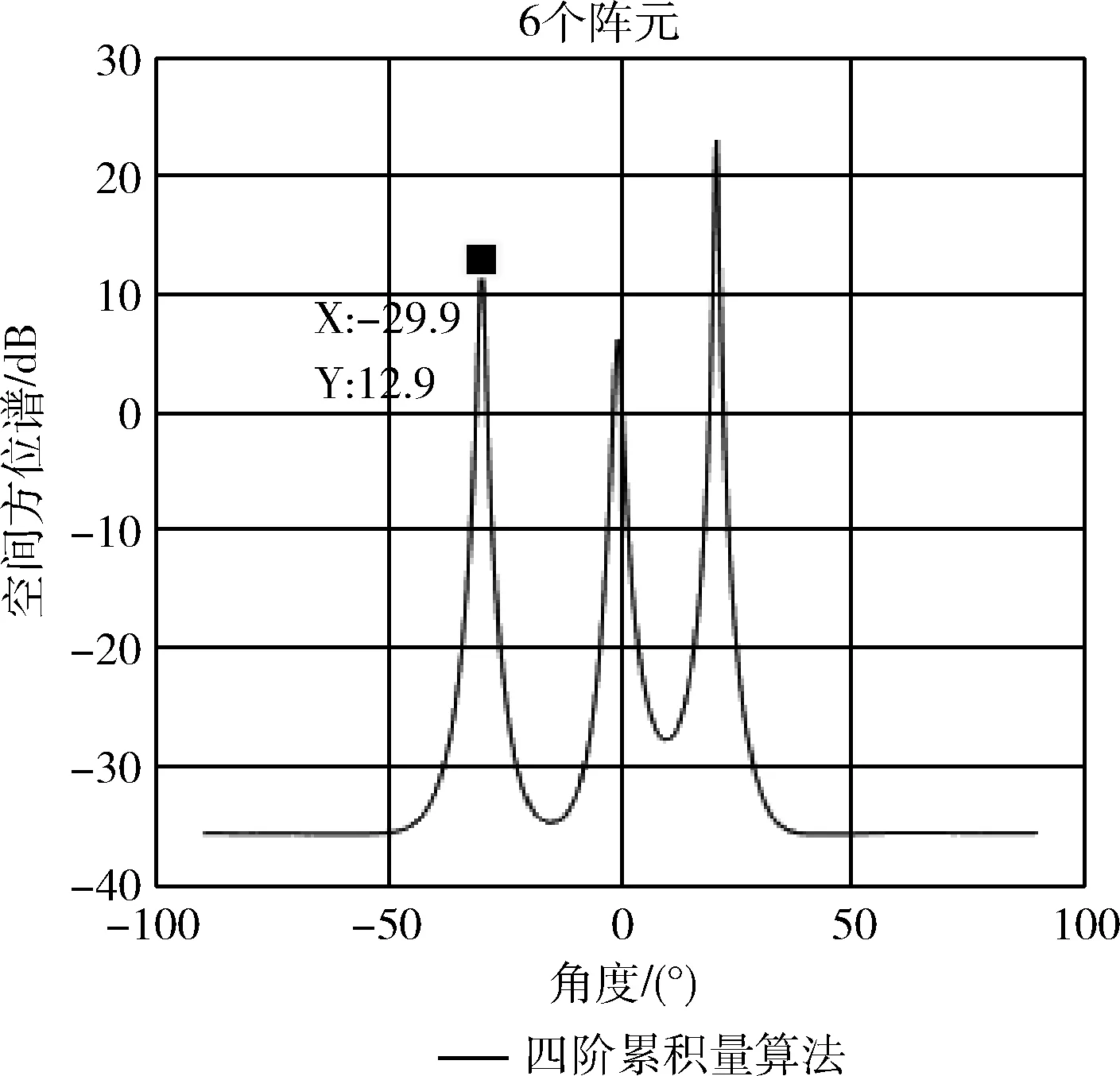
图2 异步PLC-DS-CDMA信号波达方向估计
由图1和图2知,异步PLC-DS-CDMA信号,在信噪比为-12 dB下,两种算法的估计结果偏差在1°以内,但四阶累积量的偏差更小,表明估计结果更加准确。
仿真实验二:在不同信噪比下的成功概率,分别仿真6个阵元和8个阵元下的结果,蒙特卡洛仿真200次,仿真结果如图3、图4所示。
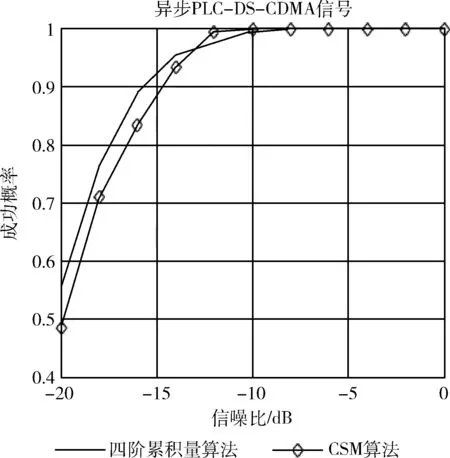
图3 6个阵元时的成功概率
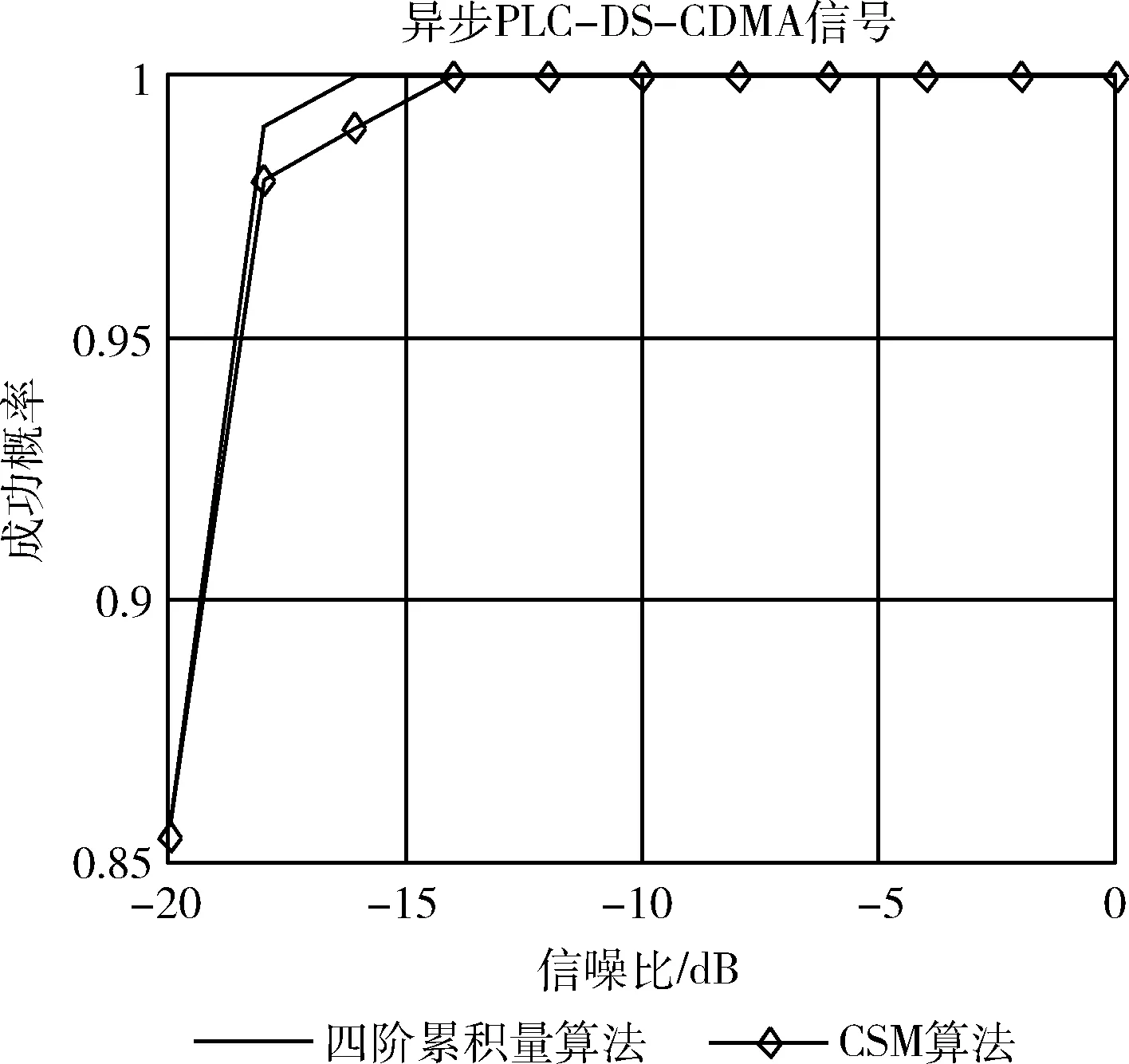
图4 8个阵元时的成功概率
从图3可以看出,6个阵元时,在-10 dB时两种算法都能达到100%正确率,从图4可知,8个阵元,在-14 dB时,成功率可以达到100%。表明阵元数越多,成功率越高,而且四阶累积量算法比CSM算法的估计结果更好。
仿真实验三:分别在6个阵元和8个阵元时,不同信噪比下异步PLC-DS-CDMA信号的均方根误差。蒙特卡罗仿真200次。仿真结果如图5、图6所示。
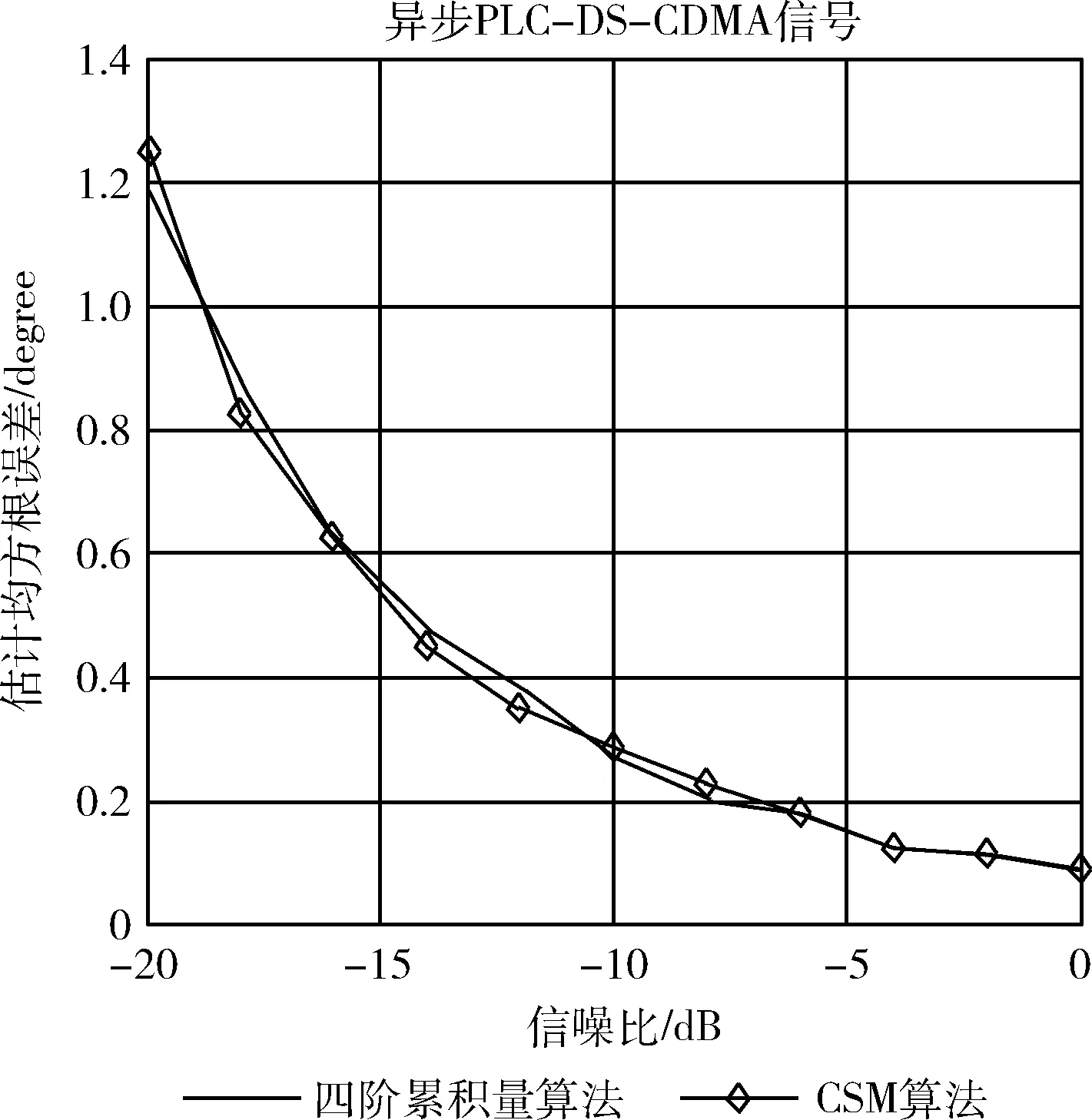
图5 6个阵元时的均方根误差
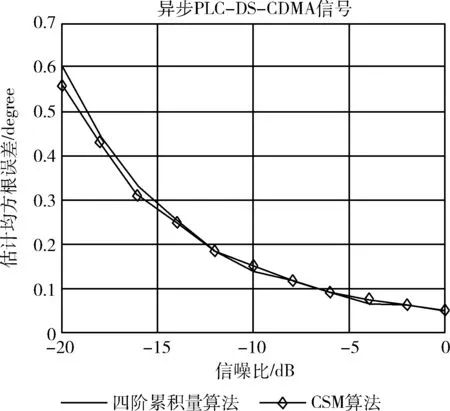
图6 8个阵元时的均方根误差
从图5和图6可知,在6个阵元,信噪比为-20 dB,两种算法均方根误差为1点多,而8个阵元时,为0.6上下,表明阵元数越多,均方根误差越小,估计效果更好,两种算法的均方根误差性能曲线图相差不大。
仿真实验四:异步NPLC-DS-CDMA信号应用两种算法在-12 dB信噪比时的波达方向估计,其中扩频码周期为127,信息码宽度为90,仿真结果如图7、图8所示。
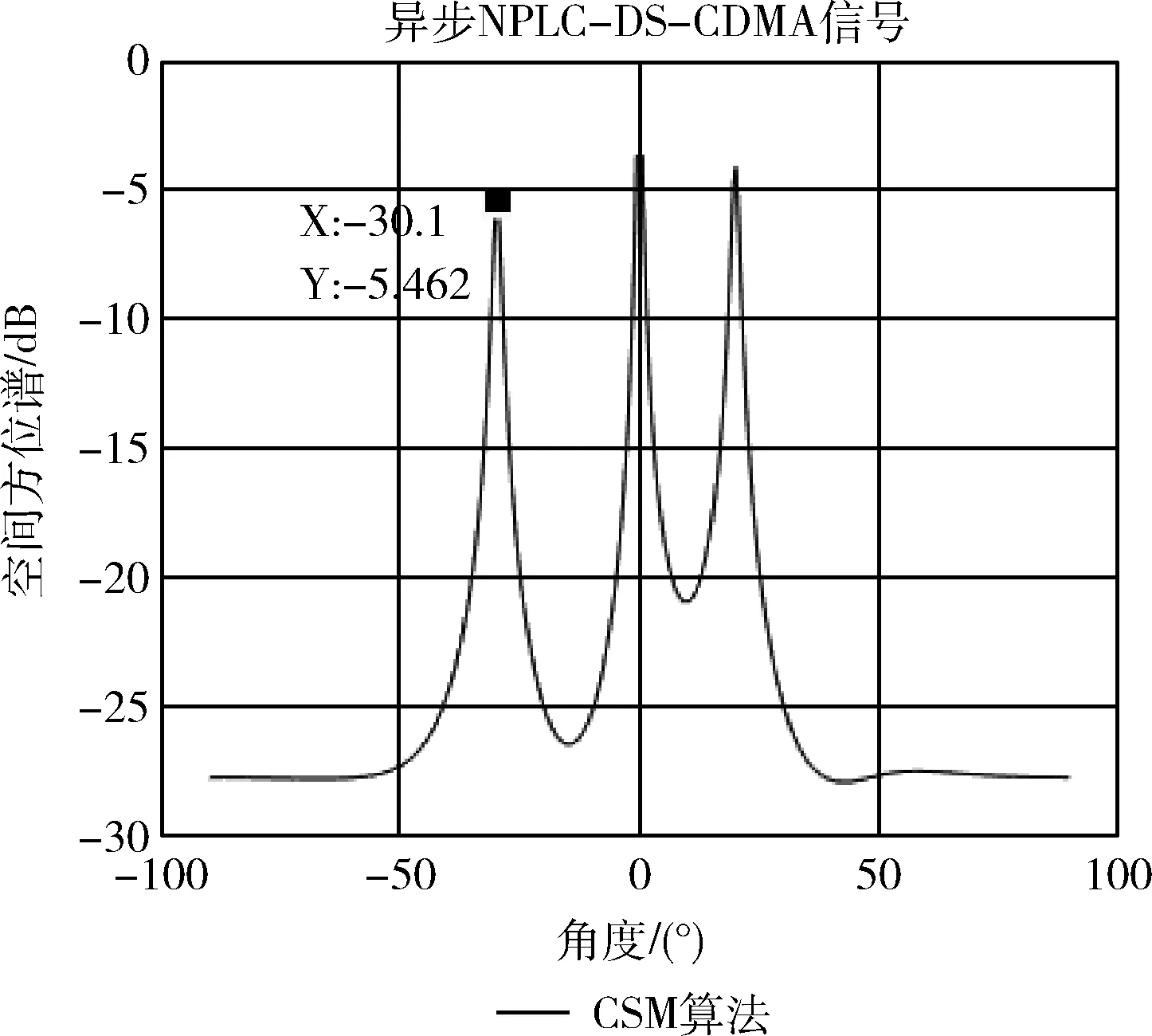
图7 6个阵元时的仿真结果
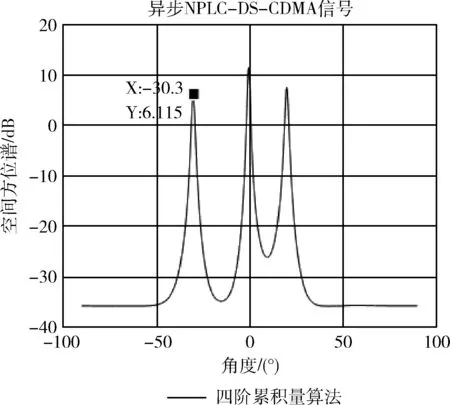
图8 6个阵元时的仿真结果
从图7和图8可知,异步NPLC-DS-CDMA信号应用两种算法同样可以估计出入射方向。
仿真实验五:异步NPLC-DS-CDMA信号用两种算法的成功率。仿真结果如图9所示。
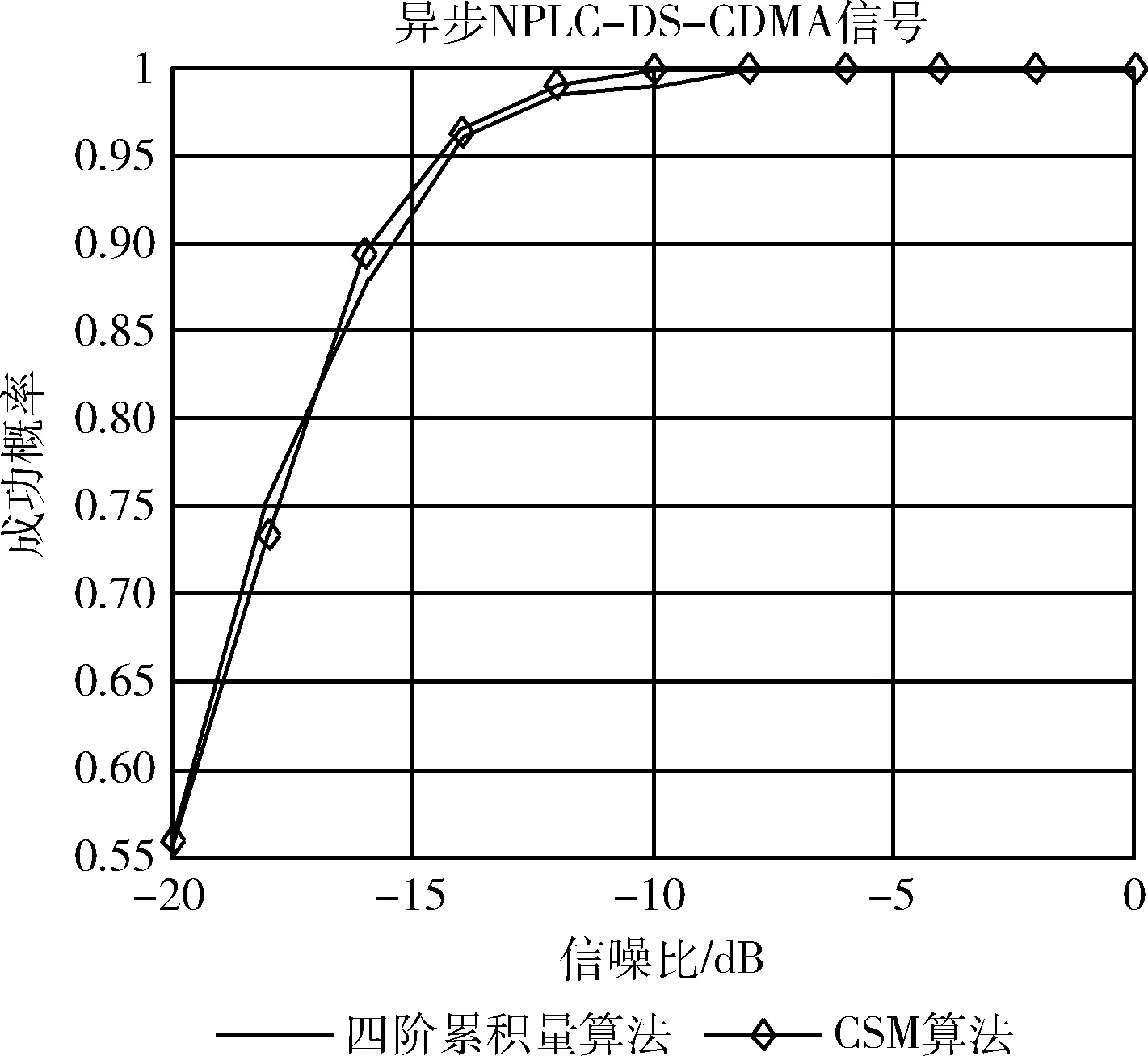
图9 6个阵元时的仿真结果
从图9看出,异步NPLC-DS-CDMA信号在-8 dB时两种算法的成功率达到100%,由仿真实验二知异步PLC-DS-CDMA信号在-10 dB能达到100%,说明两种算法对非周期信号的估计性能比周期信号差。
仿真实验六:对于异步NPLC-DS-CDMA信号不同信噪比下的均方根误差。仿真结果如图10所示。
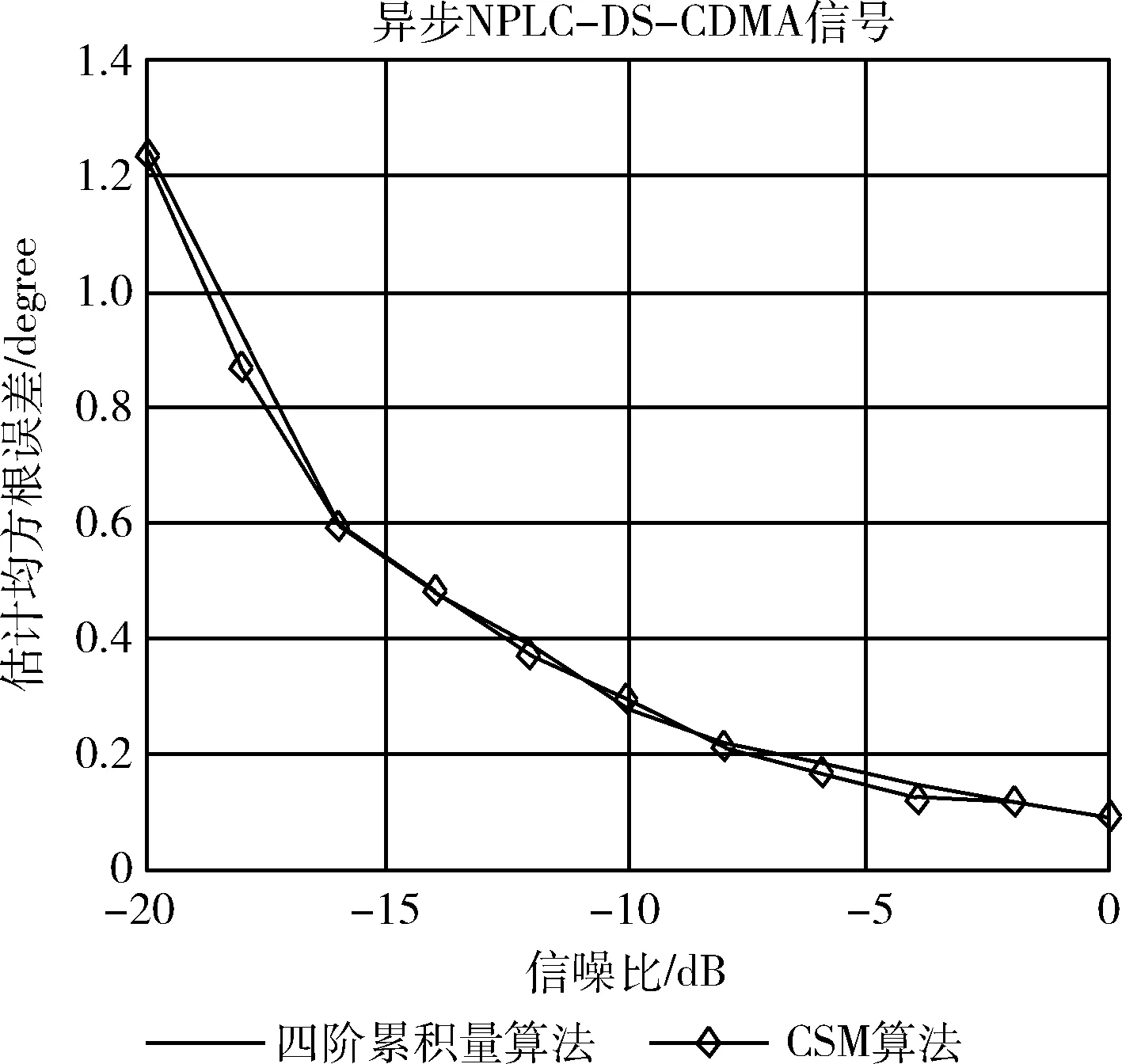
图10 6个阵元时的仿真结果
从图10看出,随着信噪比升高,异步NPLC-DS-CDMA信号的均方根误差逐渐变小。
5 结束语
本文提出用相干信号子空间算法和四阶累积量算法去估计异步LC-DS-CDMA信号的波达方向。通过计算机仿真,周期和非周期信号都能用本文所提的两种算法在信噪比下大于-10 dB时准确估计出波达方向,本文仿真了在不同信噪比下的成功率和均方根误差,验证了两种算法的正确性,四阶累积量算法比CSM算法的估计效果更好,但是四阶累量的计算量较大,仿真速度比较慢。
