边界元法几乎奇异积分计算方法及其在螺旋桨性能预报中的应用

2020-07-20管延敏黄温赟陈庆任刘可峰

江苏科技大学学报(自然科学版) 2020年3期

管延敏,陈萍,黄温赟,陈庆任,刘可峰

(1.江苏科技大学船舶与海洋工程学院,镇江 212003) (2.中国水产科学研究院渔业机械仪器研究所,上海 200092) (3.中国船级社武汉规范研究所,武汉 430022)

在船舶水动力计算诸多算法中,边界元法以其计算简便、形式多样、适应性强等优点得到众多学者的认可．边界元法在奇点接近区域进行影响系数计算时,高斯积分法存在几乎奇异积分,易产生误差,影响数值模拟精度．许多学者对提高边界元法算法精度的方法展开研究．针对非光滑边界物体切向诱导速度误差极大问题,文献[1]中提出了泰勒展开边界元方法;文献[2]中运用双层插值单元法将边界积分方程源点布置在单元内部,提高边界元法的算法精度;文献[3-5]中采用无奇异边界元法将流体计算域表面网格中心上的奇点移至计算域外部,实现了算法的无奇异化．在几乎奇异积分方面,文献[6]中对二维几乎奇异积分截断误差进行了研究;文献[7]中通过运用极坐标变换将奇异积分转化为常规积分,提出了一种高阶边界元奇异积分的通用高效计算方法;文献[8]中通过引入渐近距离函数完善了指数变换,提高了算法精度;文献[9]中提出一种自适应方法计算声学边界元中的拟奇异积分;文献[10]中运用半解析算法对三维声场边界元法几乎奇异积分问题进行了分析研究;文献[11]中对三维变系数热传导问题边界元分析中几乎奇异积分计算进行了研究;文献[12]中提出了一种弹性边界元法几乎奇异积分的半解析算法;文献[13]中提出了一种用于三维边界元法几乎奇异积分计算的二叉树细分方法．

螺旋桨作为船舶主要推进器,精确预报其水动力性能对螺旋桨、船舶优化设计具有重要意义,引起广大学者的关注[14-16]．文中采用一种影响系数精确积分的方法对几乎奇异积分进行精确计算,并将该方法应用于定常工况和非定常工况螺旋桨水动力性能预报,有效地解决了螺旋桨桨叶叶梢处几乎奇异积分问题,数值结果表明文中采取的方法精确、稳定．

1 边界元数值方法

1.1 控制方程及边界条件设定

定义光滑边界S包围的流场区域V,并假定边界S由物面SB、尾涡面SW和外边界面S∞组成,对于不可压无旋流,存在速度势φ满足Laplace方程:

(1)

当螺旋桨处于无限流域中,无穷远处扰动速度势趋近于消失,边界S∞可忽略,计算时只考虑物面SB和尾涡面SW边界条件.

(1) 物面上满足不可穿透边界条件：

(2)

式中：VI为来流速度；VA和ω分别为来流速度矢量和角速度矢量；r是边界面上点P(x,y,z)的位置矢量；n为物面外法线方向．

(2) 假设尾涡面无穷薄,通过尾涡面法向速度和压力无间断,允许速度势有跳跃,尾涡面边界条件可表示为:

(ΔP)SW=P+-P-=0

(3)

Δφ=φ+-φ-

(4)

式中，上标+，-分别代表上下表面.

1.2 基于Green定理的边界元表述

当场点P(x,y,z)位于边界面S上时,Green定理可以描述为:

(5)

将边界条件代入式(5),有:

(6)

1.3 边界积分方程离散

设桨叶、桨毂共划分为NK个单元,尾涡面划分为NW个单元,在边界每个四边形单元上布置等强度源汇和偶极子,则螺旋桨表面的每个单元形心处满足边界积分方程,积分方程式(6)可转化为线性方程组：

i=1,2,…,N

(7)

式中：

(8)

(9)

定义h为场点到积分单元的法向距离,式(8)中非对角线元素影响系数可以进一步写为:

(10)

2 几乎奇异积分的计算

由式(9、10)可见,当r趋向于0时,影响系数计算存在几乎奇异积分．文中采用一种精确积分的方法进行几乎奇异积分计算.

定义积分单元(图1)，四边形P1P2P3P4为积分单元,场点O在平面P1P2P3P4的投射点为O′．以逆时针为正向,定义有向面积Sp1p2p3p4为：

(11)

(12)

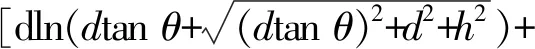
(13)

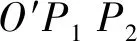
图1 积分单元分块及极坐标示意Fig.1 Integral element blocking and polarcoordinate diagram

3 数值算例

在运用边界元法预报螺旋桨水动力性能时,螺旋桨桨叶叶梢处奇点接近,存在几乎奇异积分的问题,易导致桨叶压力分布计算结果不准确、计算过程发散,为了验证上述几乎奇异积分处理方法的准确性,文中给出了螺旋桨定常、非定常性能预报的数值算例．

3.1 螺旋桨定常性能预报

DTMB4119桨(第19届ITTC推荐桨)为三叶桨,无侧斜,无纵倾,设计进速系数J=0.833,网格划分如图2．图3为敞水性能计算结果与试验值的比较,可见文中计算得到的螺旋桨推力系数KT和扭矩系数Kg与试验值相吻合,文中方法只进行简单的剖面粘性系数修正,在低进速时计算值与试验值存在较小偏差．图4给出了J=0.833时在不同径向位置r/R=0.3、0.7、0.9处叶背和叶面压力分布计算结果与试验值、Hoshino计算值的比较,可见文中所选用的几乎奇异积分处理方法对定常工况螺旋桨压力分布的预报具有很好的精度,能够准确预报叶稍区域压力分布,只在0.3R剖面处受流场粘性和桨毂形状选取影响而与试验值有一定的差距，x/C为弦长的百分比．

图2 DTMB 4119桨网格划分Fig.2 Element distribution of DTMB 4119

图3 DTMB 4119桨敞水性能比较Fig.3 Comparison of the open waterperformance of DTMB 4119

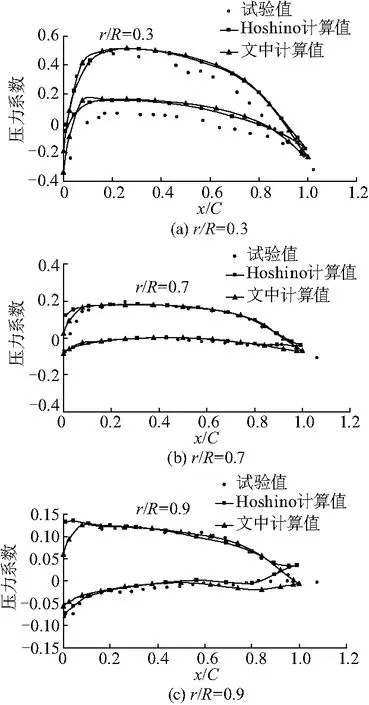
图4 DTMB 4119桨弦向压力分布Fig.4 Comparison of chordwise pressure distributionsfor DTMB 4119

3.2 螺旋桨非定常性能预报

DTMB4679桨(第22届ITTC推荐桨)为三叶大侧斜螺旋桨,试验工况J=1.078,网格划分如图5．该桨来流为斜流角为7.5°的纯斜流,如表1．图6为剖面压力分布平均值计算值与试验值的比较,一阶剖面压力分布幅值比较如图7,计算值与试验值趋势一致,结果相近,可见文中所选用的几乎奇异积分处理方法适用于非均匀伴流螺旋桨性能预报．