基于新记分函数与熵的犹豫中智VIKOR方法
2020-07-20霍礼勇
李 鹏,霍礼勇,刘 菊
(江苏科技大学 经济管理学院,镇江212003)
文献[1]中提出了模糊集的概念,通过隶属度表示模糊性,但无法表征犹豫状态.针对此问题,文献[2]中提出了直觉模糊集的概念,运用隶属度和非隶属度二维信息表征不确定性,其中隶属度、非隶属度、犹豫度3个元素之和为1.然而在现实生活中,决策者对属性进行评价时会出现隶属度、非隶属度、犹豫度相互独立的情况.文献[3]中提出了中智集的概念,用真实程度T、不确定程度I和谬误程度F3个相互独立元素表示决策信息的模糊性.
由于中智集能够更加准确地表达决策者对客观事物的看法,国内外众多学者对其进行了研究.文献[4]中提出了单值中智集的概念.文献[5]中定义了单值中智集之间的距离、相似性度量及熵公式.文献[6]中在余弦函数基础上定义了熵、相似性和交叉熵等测度的信息度量公式,并将其运用到单值中智集多属性决策问题中.文献[7]中将交叉熵拓展到单值中智集,提出了单值中智交叉熵.文献[8]中定义了单值中智数的记分函数,并提出了一种多属性中智决策方法.文献[9]中定义了一种单值中智数的新记分函数,在此基础上运用TOPSIS方法进行决策排序.文献[10]中提出了区间中智集的概念,将T、I、F以标准区间的形式表征.在此基础上,文献[11]中定义了一种区间中智熵的计算公式.文献[12]中提出了多值中智集的概念,并定义了多值中智数的期望以及Hamming距离.文献[13]中利用多值区间中智集描述不确定信息,定义了多值区间中智集的欧氏距离.由于现实中评估问题的不确定性,人们对事物进行评估时往往具有一定的犹豫性,难以用单个元素进行描述.文献[14]中提出了犹豫模糊集的概念.文献[15]中在犹豫模糊集的基础上提出了犹豫直觉模糊集.文献[16]中提出了犹豫中智集和犹豫中智元的概念.
VIKOR方法是对决策方案进行折衷排序的一种方法,从可行解中确定相对最优解,可以有效解决诸多决策问题.目前,已有大量学者对VIKOR方法进行了深入研究.文献[17]中讨论了区间数型模糊VIKOR方法;文献[18]中提出了基于直觉模糊信息的群体VIKOR方法;文献[19]中提出了区间直觉模糊信息的VIKOR方法;文献[20]中提出了基于远程指数的多元标准决策分析的广义距离度量毕达哥拉斯模糊VIKOR方法;文献[21]中构建了基于熵权法和VIKOR法的装备作战准备评估模型等.然而,基于犹豫中智集的VIKOR方法研究相对较少.文献[8-9]将记分函数引用到中智决策方法中,但存在不合理的地方,导致区分度较低.文献[16]中提出了犹豫中智集和犹豫中智元的概念,但属性权重直接给出,并未考虑确定权重的合理方法.因此,文中将VIKOR方法拓展到犹豫中智集中,提出一种新记分函数与熵的犹豫中智VIKOR方法.
1 基本理论
1.1 中智集
定义1[22]设X是一非空集合,则X上的单值中智集为A={〈x,TA(x),IA(x),FA(x)〉|x∈X}.其中,TA(x):X→[0,1],IA(x):X→[0,1],FA(x):X→[0,1]分别表示真实程度函数、不确定程度函数与谬误程度函数,0≤supTA(x)+supIA(x)+supFA(x)≤3.
便于叙述,单值中智数记为a=〈Ta,Ia,Fa〉.
定义2[23]设非空集合X={x1,x2,…,xn},M={〈x,TM(x),IM(x),FM(x)〉|x∈X}与N={〈x,TN(x),IN(x),FN(x)〉|x∈X}是论域X上的两个单值中智集,则M和N之间的欧式距离为:
(1)
1.2 犹豫中智集
定义3[24]设X∈[0,1]是一非空集合,则犹豫模糊集可表示为A={〈x,hA(x)〉|x∈X}.其中,hA(x)表示x∈X的若干种可能隶属度构成的集合,且满足hA(x)∈[0,1].
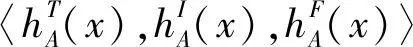
定义hA=hA(x)为犹豫中智数(HNN),记X上所有犹豫中智集构成的集合为HNS(X).
定义5[16]设X是一非空集合,X上的两个犹豫中智数为:
则hA和hB的欧氏距离为:
(2)

针对犹豫中智数中单值中智数个数不同的情况,即lA≠lB时,文中采用文献[16]中提出的方法,使两个犹豫中智数中包含相同个数的元素.
2 新记分函数
单值中智数是犹豫中智数的基本单元,而记分函数是其大小比较的有效工具,但是现有的记分函数在区分度上仍有待提高.基于此,文中分析了现有记分函数的缺陷,并在此基础上提出一种新记分函数.
2.1 现有记分函数的缺陷
例1设单值中智数a=〈0.9,0.2,0.2〉和b=〈0.9,0.1,0.4〉,根据记分函数,有:
则a~b,无法区分两个单值中智数的大小.
例2设单值中智数c=〈0.8,0.6,0.4〉和d=〈0.8,0.4,0.6〉,根据记分函数的定义:
则a~b,无法区分两个单值中智数的大小.
2.2 新记分函数
文献[25-28]中分别从不同角度提出了直觉模糊数的记分函数.由于单值中智数在性质与运算法则上与直觉模糊数有一定的相似之处,文中借鉴上述文献的思想,提出以下新记分函数.
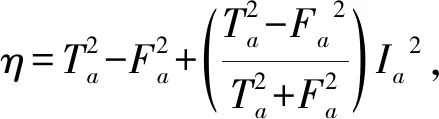
(3)
式中,Sgn为符号函数.
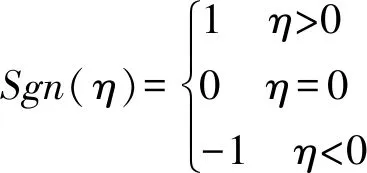
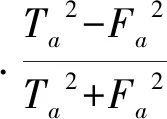
运用文中提出的记分函数对例1与例2的数据进行计算,可得S(a)=0.898,S(b)=0.657,S(c)=0.834,S(d)=0.325.可以看出,文中提出的记分函数在区分度上要强于记分函数S1和S2.
3 基于犹豫中智集的熵
熵的概念起源于热力学,是对系统不确定程度的一种描述,目前已在信息领域取得了诸多应用,其中熵权法已广泛应用于多属性决策理论.文献[29]中根据犹豫模糊元的距离测度,提出了多种犹豫模糊元的熵.文献[30]中提出了单值中智熵.然而,犹豫中智熵的相关研究尚不多见,文中提出了犹豫中智集熵的公理化定义,并构建一种犹豫中智熵的计算公式.
定义7设论域X={x1,x2,…,xn},A={〈xi,hA(xi)〉|xi∈X},B={〈xi,hB(xi)〉|xi∈X}为论域X上的两个犹豫中智集,其中

k=1,2,…,lA;i=1,2,…,n.
则熵[19,29]EN:N(X)→[0,1]满足以下性质:
(1) 0≤EN(A)≤1.
(2) 当M={〈1,0,1〉,〈1,0,1〉,…,〈1,0,1〉}时,则EN(A)=0.
则EN(A)≤EN(B).

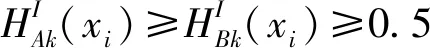

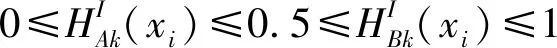
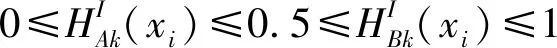
(4) 当A={〈0.5,0.5,0.5〉,〈0.5,0.5,0.5〉,…,〈0.5,0.5,0.5〉} 时,则EN(A)=1.
(5)EN(A)=EN(AC).
根据定义7,定义一种犹豫中智熵的计算公式.
定义8设非空集合X={x1,x2,…,xn},犹豫中智集A={〈xi,hA(xi)〉|xi∈X}的犹豫中智数为:
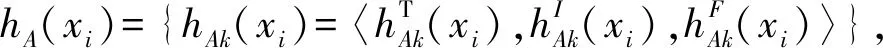
则A的熵为:
(4)

例3设犹豫中智数{〈0.8,0.5,0.4〉,〈0.7,0.3,0.5〉},则根据式(4),其熵的计算结果如下:
定理1EN满足定义7中的性质(1)~(5).

可得:
所以,
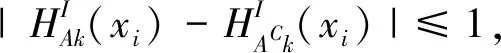
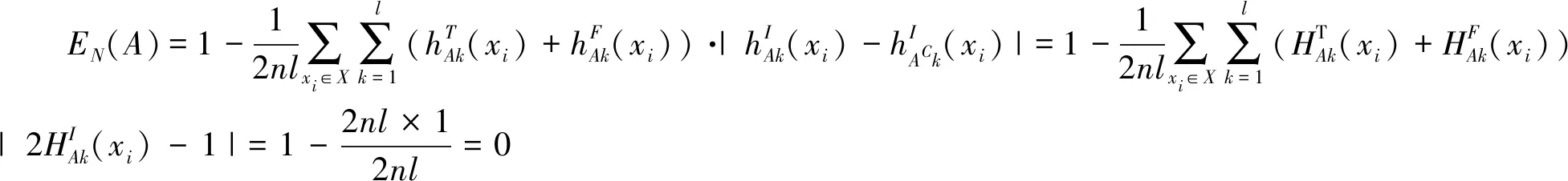
因此,当A={〈1,0,1〉,〈1,0,1〉,…,〈1,0,1〉}时,则EN(A)=0.

可得,
所以,EN(A)-EN(B)≤0,即EN(A)≤EN(B).

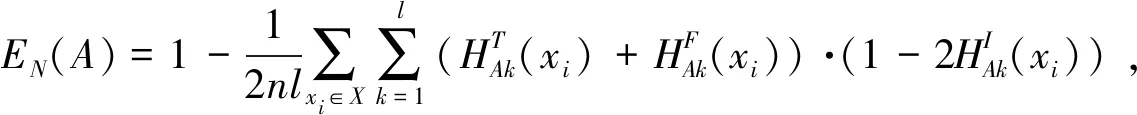
所以,EN(A)-EN(B)≥0,即EN(A)≥EN(B).
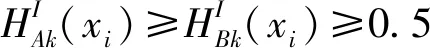
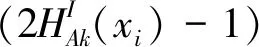
所以,EN(A)-EN(B)≤0,即EN(A)≤EN(B).


可得:
所以,EN(A)-EN(B)≥0,即EN(A)≥EN(B).
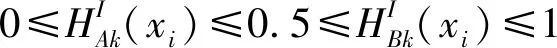
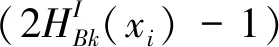
可得,
所以,EN(A)-EN(B)≤0,
即EN(A)≤EN(B).
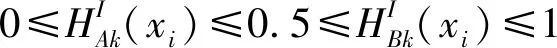
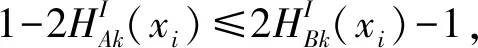
可得,
所以,EN(A)-EN(B)≥0,即EN(A)≥EN(B).
(4) 当A={〈0.5,0.5,0.5〉,〈0.5,0.5,0.5〉,…,〈0.5,0.5,0.5〉}时,
因此,当A={〈0.5,0.5,0.5〉,〈0.5,0.5,0.5〉,…,〈0.5,0.5,0.5〉}时,即EN(A)=1.


因此,定理得证.
4 基于新记分函数与熵的犹豫中智VIKOR方法
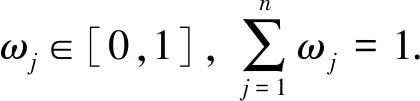
文中在研究过程中主要采用理论研究和案例分析相结合,通过分析总结现有研究成果,将VIKOR方法拓展到犹豫中智集中,提出一种新记分函数与熵的犹豫中智VIKOR方法.其中,VIKOR方法对每个方案进行排序.新记分函数克服传统记分函数分辨率不高的缺点,目的是为了给添加平均值的犹豫中智数中的单值中智数进行降序,熵是为了给每个属性进行赋权.
犹豫中智信息VIKOR方法的决策流程如下:
步骤1 根据犹豫中智熵确定属性权重
根据犹豫中智决策矩阵H=(hij)m×n与式(4),可得属性权重如下:
(5)
步骤2 确定犹豫中智数的正、负理想方案
确定犹豫中智数的正理想方案:
确定犹豫中智数的负理想方案:
需要指出的是,文中采用文献[16]的增加元素方式确定正、负理想方案,使同一属性下的犹豫中智数中单值中智数的个数相同,且利用新的记分函数对单值中智数进行降序排列.其中,l表示每个属性下各方案中犹豫中智数中单值中智数的个数.
步骤3 计算最大群体效用值Si和最小个体遗憾Ri
(6)
(7)
步骤4 获取折衷评价值Qi
(8)
式中:i=1,2,…,m;j=1,2,…,n;k=1,2,…,l,l为犹豫中智数中单值中智数的个数.式(8)中,S+=minSi,S-=maxSi,R+=minRi,R-=maxRi.在VIKOR方法中,λ一般取0.5,表示根据赞同的情况进行决策,含义是决策机制系数或最大群体效用权重.
步骤5 对备选方案进行排序
对Si、Ri和Qi进行排序,其中,Qi值越小,表明方案越好;反之越差.步骤如下:
条件1(可接受优势):Q2-Q1≥1/(m-1),m是方案的总数目.文献[32]中提出当m≤4时,取1/(m-1)=1/4.条件2(可接受稳定性):如果Q1在序列Si或Ri中排列也是最优,则Q1在决策中是最优,且最稳定.
如果两个条件都成立,则此选中的方案为最佳决策,Q1表示最优方案排在第1位,Q2表示最优方案排在第2位.
如果两个条件满足条件1,则折衷排序的一组妥协解Q1、Q2都为最优解;当满足条件2时,根据Qξ-Q1<1/(m-1),可得到最大值ξ,则Q1,Q2,…,Qξ都接近理想方案.
5 算例分析
企业的发展离不开精湛的管理,为了使企业不被淘汰,管理模式亟待创新.因此,精益生产管理很快流入各企业的管理模式中.某企业需要学习先进管理模式,通过调研发现有Y1,Y2,Y33家企业综合情况与本企业大体相同.根据专家调研、实地考察和文献资料构建属性,分别为G1,G2,G3,G4.其中,G1为拉动式准时化生产;G2为全面质量管理;G3为团队工作法;G4为并行工程.邀请专家对上述3家企业的4个属性进行评价,得到犹豫中智决策矩阵H(表1),现对该3家企业进行排序择优.

表1 决策矩阵HTable 1 Decision matrix H
5.1 决策步骤分析
利用文中的VIKOR方法解决上述企业选择决策问题,决策流程如下:
步骤1 根据表1的决策矩阵H与式(5),求得各属性权重:
ω=(0.284,0.237,0.328,0.151)
步骤2 确定犹豫中智数的正、负理想方案
采用中庸态度添加元素原则使同一属性下各企业中犹豫中智数中单值中智数的个数一致,如表2;利用新的记分函数式(3)对单值中智数进行降序排列,如表3:

表2 添加平均值的决策矩阵Table 2 Decision matrix added the average value

表3 降序排列的决策矩阵Table 3 Decision matrix using descended order
确定犹豫中智集的正理想方案:
确定犹豫中智集的负理想方案:
步骤3 根据式(2)、(6)、(7)求出Si,Ri值.
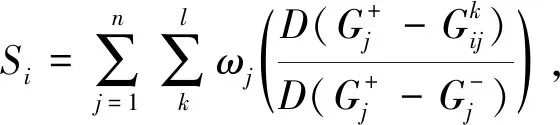
S1=0.620,S2=0.575,S3=0.630
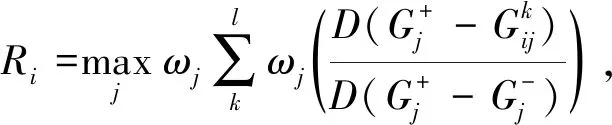
R1=0.192,R2=0.216,R3=0.279
步骤4 根据式(8)求出Qi值.

Q1=0.410,Q2=0.138,Q3=1.000
步骤5 采用文中的决策方法对Si、Ri和Qi进行排序,其中,Qi值越小,表明企业越好;反之越差,如表4:

表4 各企业的Si、Ri、Qi值以及排序Table 4 Si,Ri,Qi values and ranking orders for each enterprise
由表4可知,根据折衷评价值Qi得到企业的优先序为Y2≻Y1≻Y3,则最优企业为Y2.Q2-Q1=0.410-0.138=0.272>0.25,且满足条件(1),同时企业Y2在Si排名仍为最优方案.因此,企业Y2的精益生产管理模式在决策过程中是稳定的最优企业.
5.2 算例对比分析
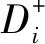
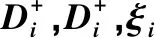
表5 TOPSIS方法中各方案的值及排序Table values and ranking orders for each enterprise using TOPSIS method
通过TOPSIS的方法可得出Y2≻Y1≻Y3.可以看出,TOPSIS方法与文中提出的方法排序结果一致,从而验证方法有效性.
通过对比,采用TOPSIS方法得出的ζi值都很接近,区分度较低,特别是企业Y1和Y3,而VIKOR方法的折衷评价值的区分度高.主要原因是TOPSIS方法在实际应用中,存在方案增减导致的逆序性问题,应用到文中选择先进企业管理模式的案例中,适应性较低,而文中提出的基于折衷思想的VIKOR方法,从追求满意解的角度去解决多属性决策,避开了TOPSIS方法的逆序性问题,在实际应用中,具有较强的实用性与可行性.
6 结论
(1) 文中分析了传统记分函数的缺陷,并在此基础上提出一种新记分函数,克服传统记分函数分辨率不高的缺点;
(2) 提出了基于犹豫中智集熵的公理化定义,设计了一种犹豫中智集的熵公式,给文中各指标进行赋权,并证明了该熵公式满足熵的公理化定义;
(3) 提出了基于犹豫中智集的VIKOR方法,并通过与传统的TOPSIS方法进行对比,分析了传统方法应用在实际案例中存在的问题,验证了文中方法的有效性与合理性.
