多柔性圆柱体受力状况对涡激振动模态影响的风洞试验研究
2020-07-20李吉祥范晨光
李吉祥,范晨光
(西南交通大学,四川成都 611756)
处于流体中的结构,当流体经过结构时会对其产生横或纵的激励,引起结构的振动,当涡脱的频率达到某个值时与结构发生涡振,严重影响结构的稳定性和安全性。涡激振动中最为典型的代表就是圆柱体的绕流。
对于流体流经柔性体产生的耦合振动问题,随着实验设备、振动测试技术以及计算机模拟水平的发展,也逐渐展开。Zhang[1]在肥皂膜水洞中进行了两并行排列丝线耦合摆动的实验, 结果表明同样来流条件下当丝线距离较近时二者表现为同向摆动,距离较远时呈反向摆动,并且反向摆动的频率明显高于同向摆动的频率。王思莹等[2]在风洞中进行了两相同薄膜旗帜的吹风试验,测量了旗帜并行排列时的模态转换临界参数。试验结果表明,两并排旗帜的稳定临界速度随无量纲排列间距的不同有所变化。文献[3]从理论上对三层板状结构在轴向流中振动特性进行了研究,分析了系统失稳的临界流速与失稳模态,着重研究了质量比和边界支承条件的影响。
为了解细长柔性管的涡激振动特性,校核经验模型,国内外的研究者开始对柔性立管涡激振动进行研究。WU[4]详细介绍了2000年以来近十年的关于柔性体长圆柱结构的涡激振动研究进展,如双共振、多模振动、非定常锁定、三次谐波和高次谐波流体力以及行波主导响应等。Trim et al[5]做了一系列关于大长径比柔性立管的涡激振动实验,发现当涡激振动的频率保持不变时,立管结构的响应模态突然由二阶锁定转移到三阶锁定。Wilde.J.J[6]在均匀流场条件下进行了长径比为788的立管涡激振动试验,捕捉到了立管复杂的三维振动响应情况。唐国强等[7]研究了大长细比的柔性立管在均匀流作用下的涡激振动问题,发现顺流向的主导频率为横流向的2倍,并且横流向以及顺流向的位移响应随着流速的增大而缓慢增加。姚宗等[8]进行了流速分层流场中细长柔性立管涡激振动试验,结果发现流速增大层立管流向弯曲曲线的最大弯曲点偏向于流速增大层的作用段,立管流向和垂直流向振动的频率分布表现为集中和分散两种形式。此外,还有不少学者采用数值模拟的方式对柔性立管进行研究[9-11]。
从现有研究成果来看,对于多根细长柔性体排列的涡激振动试验研究比较少。本文通过风洞实验研究多个柔性圆柱体,在不同风速以及不同轴向力下的加速度响应,分析获得涡激振动的频率、模态、风速与相关参数的联系。以期从实验角度分析多柔性体涡激现象产生的力学机理。
1 试验概况
试验模型采用PVC管材制作,使用了加速度传感器,传感器分布在管材的垂直于风向的x、y方向上,最大程度的减小对于实验结果的影响。同时为了更好的修正试验结果,同步使用了激光传感器进行修正。
试验在西南交通大学空气动力学实验室中进行,风洞为低速回流式风洞,直径1.2 m,最大风速为40 m/s。本试验采用Wavebook数据采集系统进行动态相应的数据采集,使用DASYLab软件进行数据的采集和分析。
试验立管排列方式如图1所示。

图1 试验立管排列方式示意
2 自振频率及临界风速的理论计算
2.1 自振频率的计算
在进行多柔性圆柱体排列状况对涡激振动模态的影响的风洞试验研究之前,有必要先来计算圆柱立管的自振频率。
当锁定发生时,有f=fst=fn,圆柱立管的实际振动频率是f,fn为立管的自振频率, 而fst是涡释频率,所以只要计算出fn就能够确定出大致的fst大小,可以利用式(1)来确定流速的大小
(1)
把计算出来的理论上的发生锁定时的临界风速值与风洞试验室能够达到的最大风速值相比较可以得出在实验过程中可能被激发出的最高阶模态,这样就可以来确定传感器的布置方案。
立管可以看作两端简支,根据立管材料的特性,那么可以采用以下三种方法来计算频率:
(1)当顶部施加的力很大时,立管的弯曲刚度实际上是可以忽略的,那么振动可按张紧的绳考虑[12],
(2)
式中:T是立管的平均张力,n是模态数,m是立管的重量,L为立管的长度。
(2)当顶部施加的力很小时 ,立管的抗弯刚度不可忽略,这时立管相当于一个不受拉的梁,计算公式[12]见式(3),
(3)
式中:I是截面惯性矩,E是立管的弹性模量,n,m,L同上。
(3)如果立管的抗弯刚度和顶部施加的力都必须考虑,则需按照式(4)计算[12],
(4)
通过前文说明的“锁定”时频率之间的关系fst=fn,s-beam,利用式(1)进行估算可获得激发各阶模态所需要的流速,即式(5)。
(5)
在获得实验可以达到的最大流速为Umax时,可以用以上几式求得振动过程中可能激发的最高模态nmax。
2.2 理论临界风速的计算
试验条件处于亚临界雷诺数范围内,此时斯特罗哈尔数约为0.2[13],当结构频率等于漩涡脱离频率时,可以推得:
(6)
式中,St为斯特罗哈尔数,D、m、H、L均为定值,当拉力T一定时,改变流速,使上式满足时,结构发生涡激振动现象。
本次试验采用空心PVC管(外径110 mm),线密度约为ρ=80g/cm(包含受拉结构);
式中:L为实验管顶(底)部与上(下)风壁面的距离,为16.3 cm;风洞风速U=0~20 m/s;管子长度H=150 cm;
将数据代入式(6)化简可得:
T=22.051U2
(7)
当对管子施加一定拉力时,可以由上式推算结构的发生涡激振动的临界风速。
3 实验结果及现象描述
3.1 不同工况下圆柱立管的实验现象分析
本次试验一共做了四个工况,不同工况的三根立管间距为120 mm,施加的力各不相同,具体见表1。

表1 不同工况下加载的力的大小 N
3.2 工况Ⅰ
三根立管施加的力均为150 N。图2为风速2.7 m/s时三根立管的时程曲线和频谱图,其中图线依次为1号立管x,y方向数据、2号立管x,y方向数据以及3号立管x,y方向数据,可以看出图像接近正弦曲线,说明立管已经开始产生涡激振动。
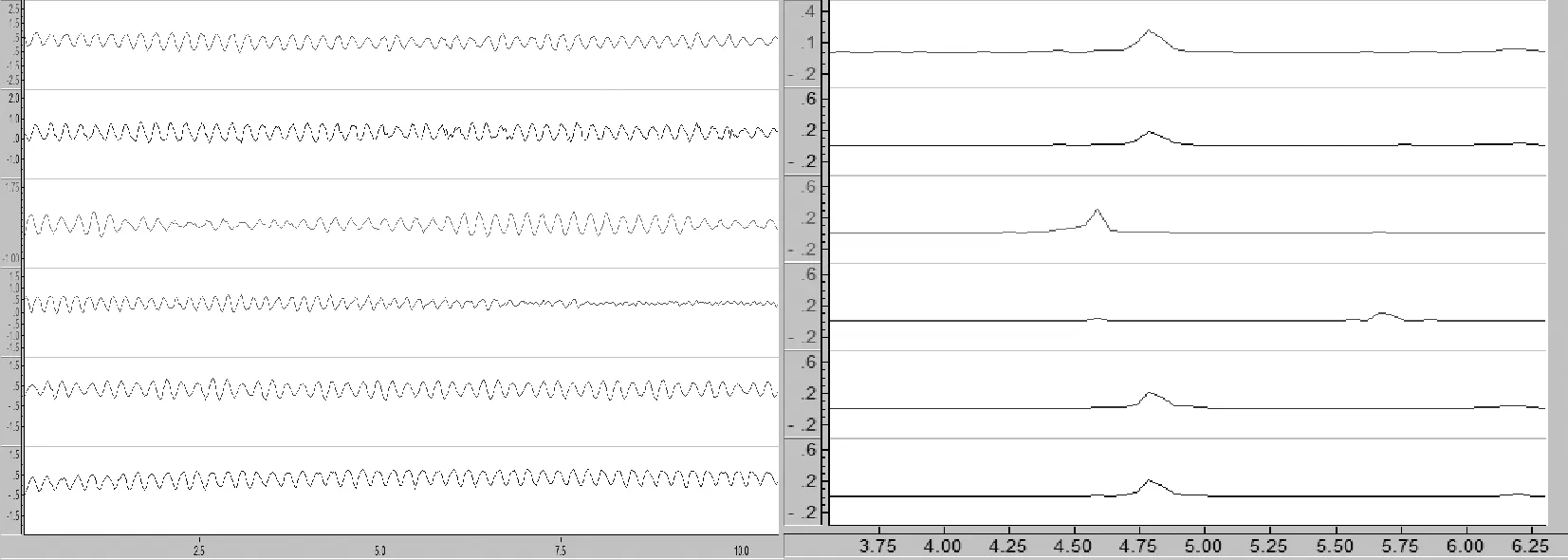
图2 风速2.7m/s时工况Ⅰ的时程曲线和频谱
随着风速的渐渐增大,三根立管的振幅也越来越大,当风速超过6 m/s时,振动已经非常剧烈,图像也变的不规则起来。实验过程中的最大风速为9 m/s,最小风速为2 m/s。把采集到的数据画出立管振动的加速度与时间的关系图像以及振幅和频率三维图,0、2、4通道分别为3、2、1号立管的x方向的加速度,1、3、5通道分别为3、2、1号立管的y方向加速度,见图3。
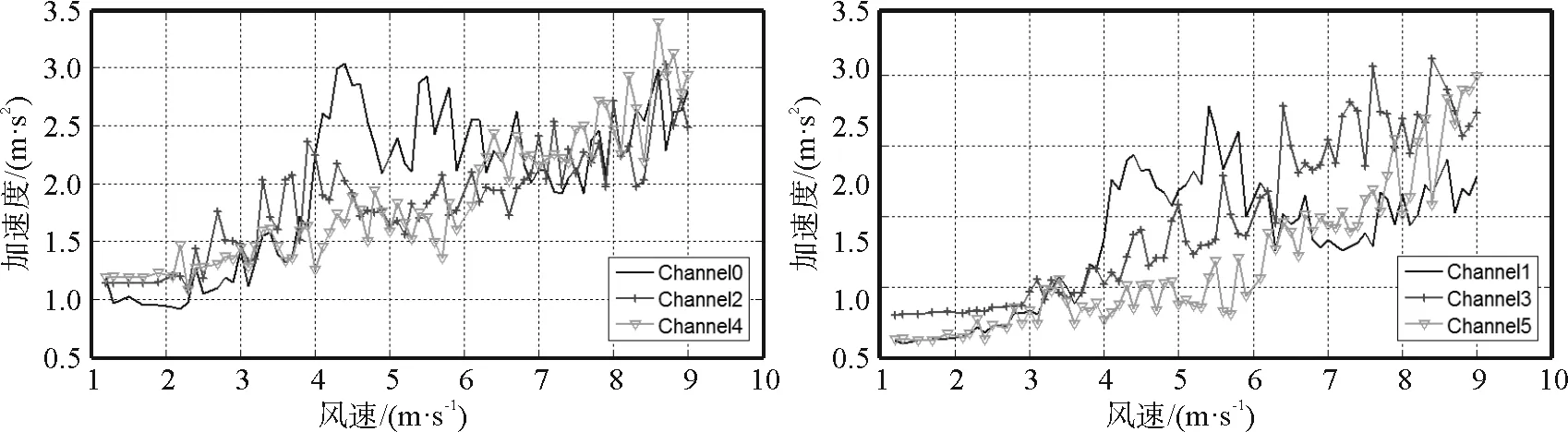
图3 工况Ⅰ时的加速度与风速的关系
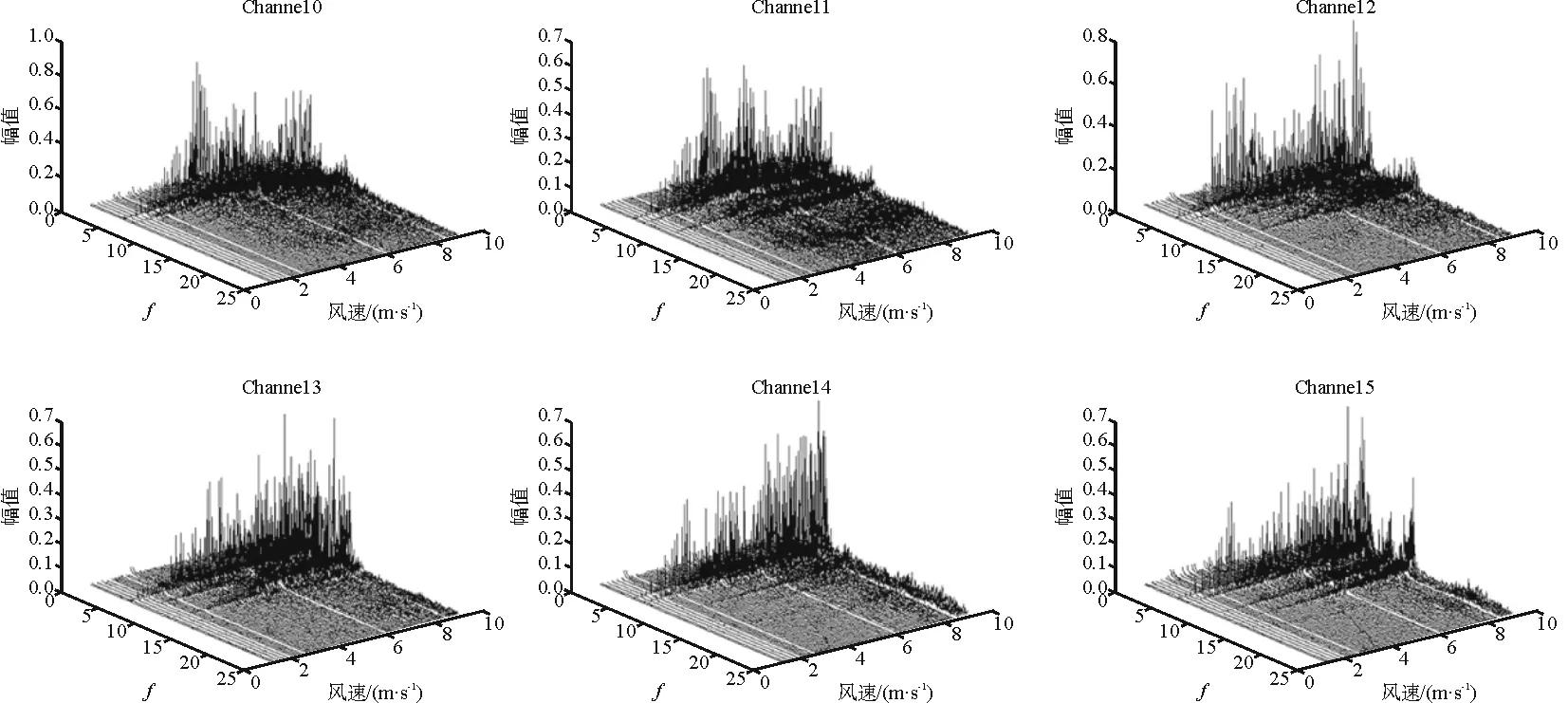
图4 工况Ⅰ时的振幅、频率与风速的三维图像
图3中0、2、4通道分别为3、2、1号立管的x方向的加速度,1、3、5通道分别为3、2、1号立管的y方向加速度,后文中与此相同不再赘述。
3.3 工况Ⅱ
三根立管的施加的力均为250 N。继续对立管加力,至250 N。在无风状态由立管自由衰减振动,得出自振频率,自振时程曲线与频谱见图4、图5。
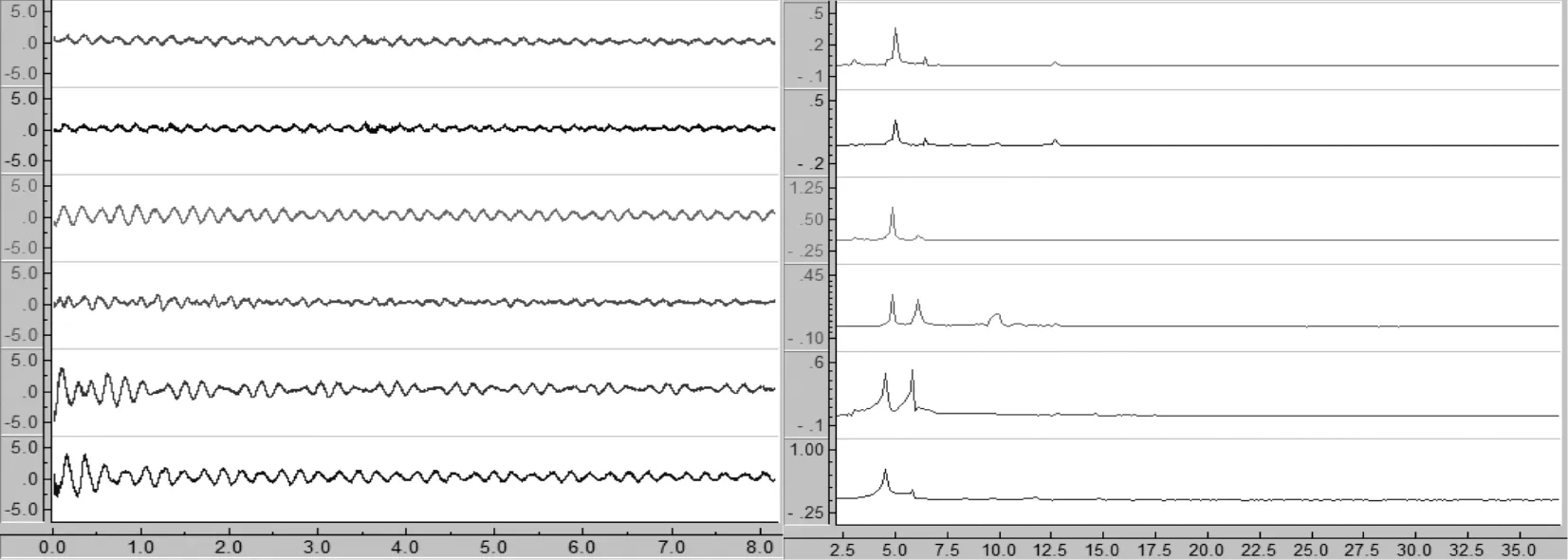
图5 工况Ⅱ下立管的自振频率
从图3中可以看出三根立管的频率都在5 Hz左右,说明他们所受的拉力是相等的。在逐渐加大风速的过程中,在风速达到3.3 m/s时,2号及3号立管发生振动,而1号立管则振动无明显规律,见图6。

图6 工况Ⅱ在风速3.3m/s下的时程曲线和频谱
从右侧的频谱图可以发现,明显的单峰曲线,说明此时的2、3号立管发生涡激振动。当风速超过5 m/s时,三根立管都发生明显的无规则振动。继续加大风速到9 m/s,得到加速度与风速的关系图(图7)以及振幅和频率三维图(图8)。
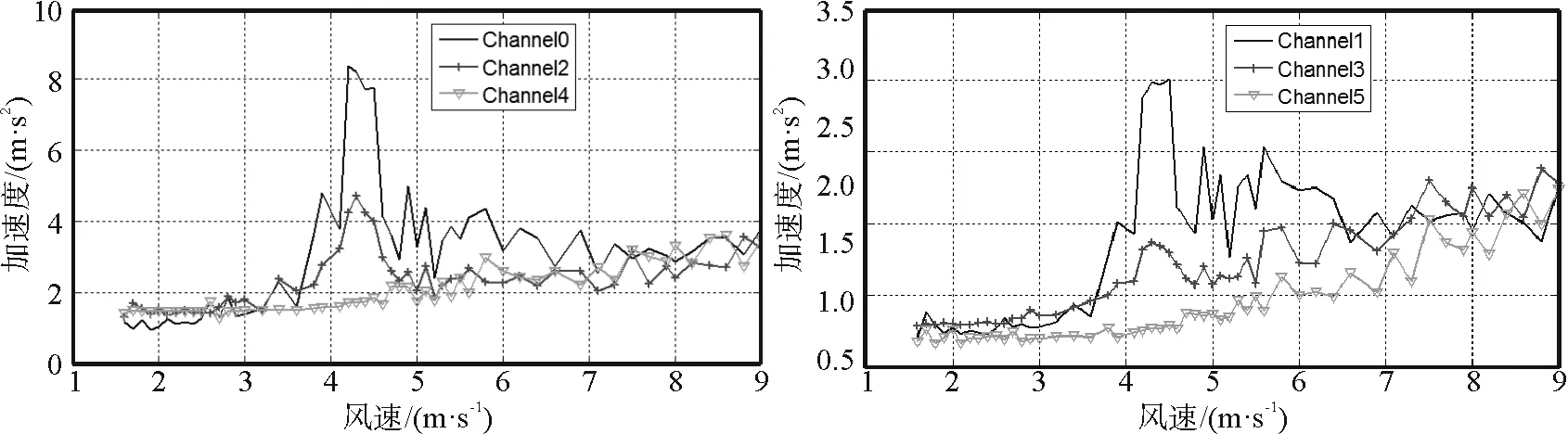
图7 工况Ⅱ时的加速度与风速的关系
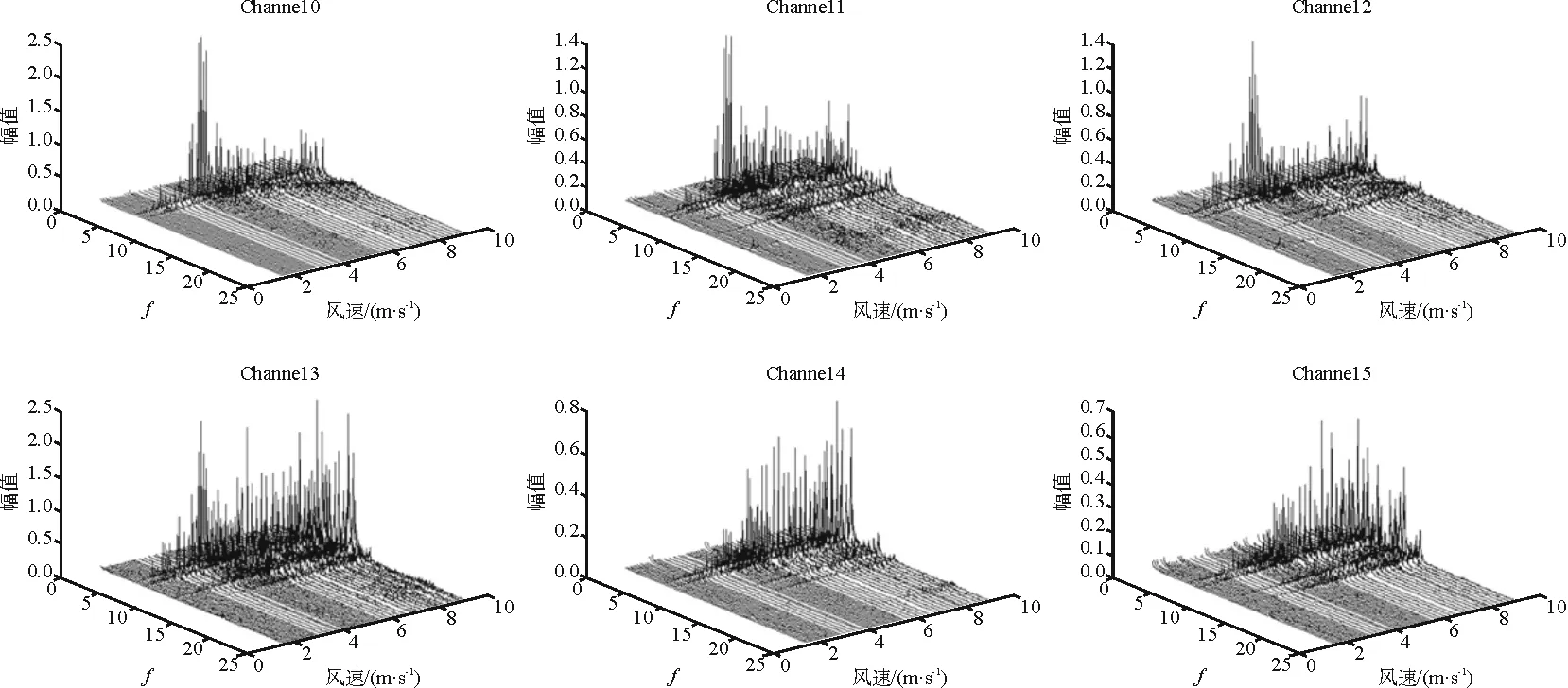
图8 工况Ⅱ时的振幅频率与风速的三维图像
3.4 工况Ⅲ
将1号立管的力减小为150 N,2、3号立管仍保持250 N。同样的,为了保证1号立管的力施加的准确性,在无风状态下对三根立管施加冲击,测得其自振频率与150 N时相同。逐渐加大风速,在风速达到2.8 m/s时,三根立管发生明显振动(图9)。
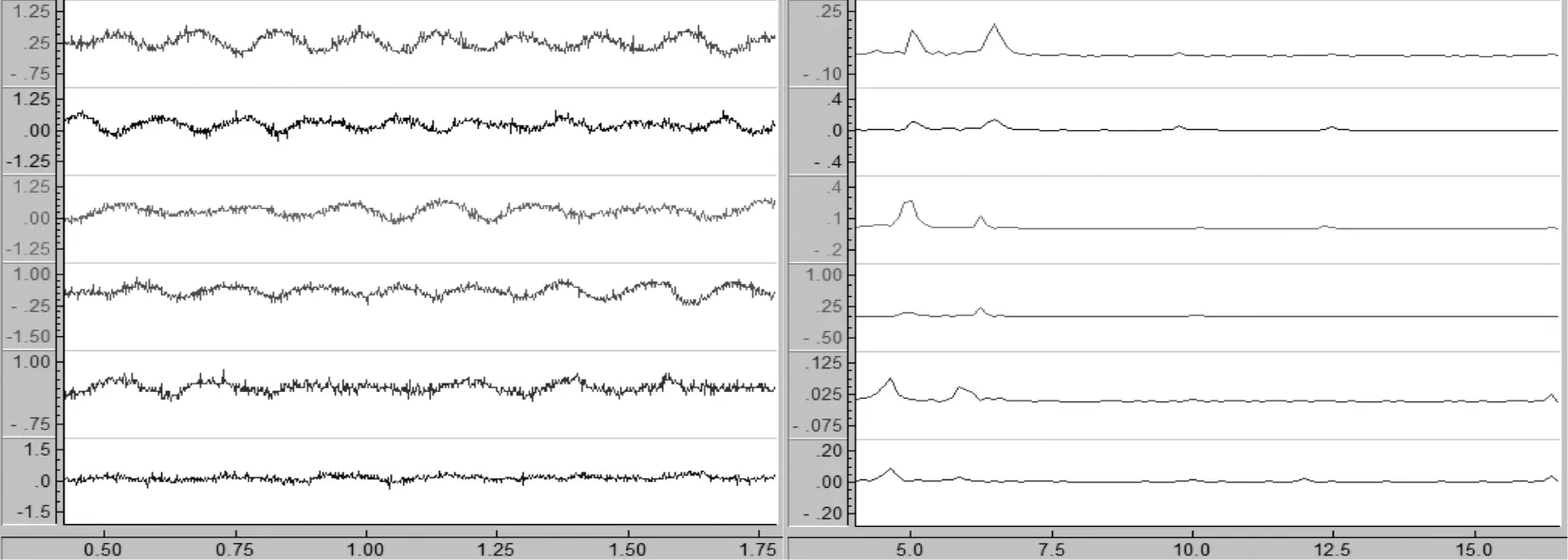
图9 工况Ⅲ下风速2.8m/s时的时程曲线和频谱
逐渐加大风速,达到9 m/s后将数据做出加速度与风速的关系图像(图10)以及振幅和频率三维图(图11)。

图10 工况Ⅲ时的加速度与风速的关系

图11 工况Ⅲ时的振幅频率与风速的三维图像
3.5 工况Ⅳ
1号立管为250 N,2、3号立管施加150 N的力。在无风状态下,对三根立管分别施加一个冲击,来测量立管的自振频率,保证其施加的力的准确性见图12。

图12 工况Ⅳ的立管自振频率
接着继续增大风速,风速在2.6 m/s时,图像趋于稳定,2、3号立管发生涡激振动如图13所示。
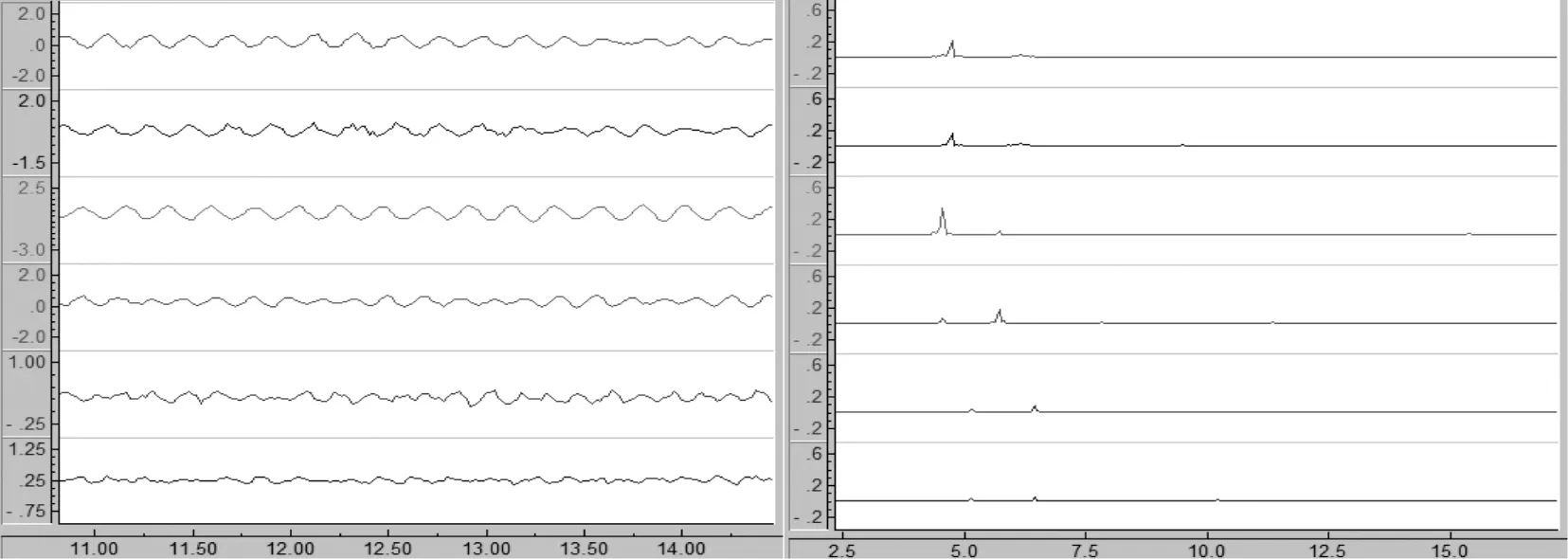
图13 工况Ⅳ在风速2.6m/s时的时程曲线和频谱
从频谱图中观察发现,2、3号立管时单峰曲线,说明此时已经发生振动。风速达到5.6 m/s后,立管振动明显增大,图线也开始不稳定,风速达到9 m/s后,做出加速度与风速的关系图像(图14)以及振幅和频率三维图(图15)。
4 结论
本试验通过采集多柔性立管在x、y方向的加速度,详细探讨了圆柱立管空气绕流的情况。并且采集多个不同工况下的加速度响应,对数据进行处理,具体分析了四种不同轴向加载工况的情况下三根立管的涡激振动情况。
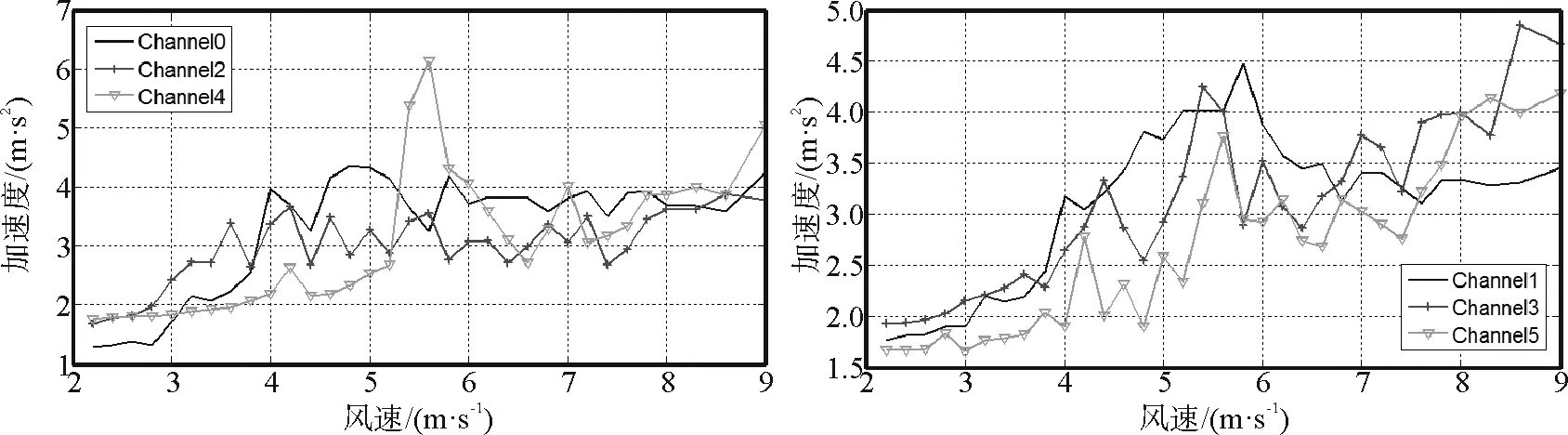
图14 工况Ⅳ时的加速度与风速的关系
通过对实验结果的分析和整理,如表2所示:
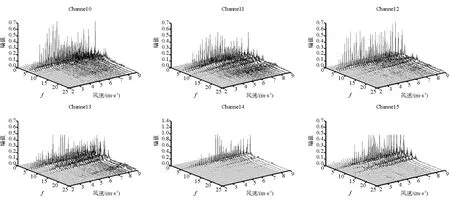
图15 工况Ⅳ时的振幅频率与风速的三维图像

表2 不同工况下的临界流速以及相位关系
对上表分析可以得出:
(1)理论计算的临界流速跟实验结果比较接近。
(2)在本文实验条件下,通过观察立管的相位情况,3号立管最容易发生涡激振动,且其相位大部分工况下是与2号立管相反的,而1号立管则很少发生振动。
(3)顺流向不同位置的立管之间受流体诱发振动相互影响,振动相位关系及振幅与所在位置及轴向约束力有关。
