基于ABAQUS非饱和膨胀土边坡降雨入渗分析
2020-07-20王金淑
饶 鸿,王金淑,吴 光
(西南交通大学,四川成都 611756)
降雨是影响边坡稳定性的主要因素之一,研究降雨入渗过程边坡稳定性的变化及边坡内部渗流场和应力场的变化规律具有重大意义[1]。
Fredlund[2]等应用Galerkin有限元法模拟暴雨条件的土坡渗流及稳定性分析;吴宏伟[3]等针对香港地区典型非饱和土边坡模拟分析多种因素影响下边坡渗流场的变化规律及稳定性评价;李炎隆[4]等基于ABAQUS有限元软件结合降雨入渗的边界条件,进行降雨入渗边坡的稳定性分析。降雨入渗非饱和土边坡,土体吸力降低抗剪强度下降,进而影响边坡稳定性。根据非饱和土力学:基质吸力是影响非饱和土性质的主要参数之一,非饱和土的强度、变形和渗透性等都与非饱和土吸力值密切相关[5]。本文以贵州省某地区膨胀土为研究对象,结合室内实验数据建立非饱和土土水特征曲线模型,基于ABAQUS有限元软件建立边坡模型,导入膨胀土土水特征曲线公式,考虑降雨过程非饱和土的吸力变化和强度衰减分析降雨入渗下非饱和膨胀土边坡的渗流场变化和流固耦合分析,探究降雨过程边坡渗流场、位移场、稳定性的变化规律。
1 计算原理及方法
1.1 饱和-非饱和理论
降雨在非饱和土中渗流满足质量守恒定律,以达西定律为基础结合渗流过程中流体质量守恒推导出以基质势为因变量的渗流控制方程[3]:
(1)

(1)初始条件:一般在模型中指定初始地下水位或进行稳态计算定义渗流初始条件。
h(x,y,t)=h(x,y,t0)
(2)
(2)定水头边界条件:在降雨入渗边界上各点的水头在某时间段内是已知的。
h|Γ1=h1(x,y,t)
(3)
(3)流量边界条件:单位面积流量q可以被赋予到边界某部分,或者水头函数的法向导数被赋予到边界。
(4)
1.2 流固耦合方程
根据虚功原理和质量守恒定理获得渗流场与应力场耦合的平衡方程和渗流连续性方程,再通过划分边坡渗流场为有限单元组合,结合边界条件采用Galerkin有限元解法将坡面方程与渗流控制方程联立求解,推导流固耦合方程[1]:
(5)
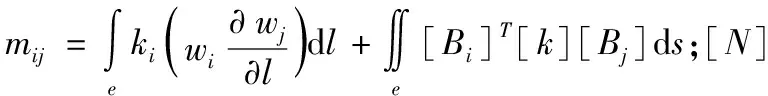
1.3 非饱和土抗剪强度公式
国内外众多学者基于土体强度试验数据提出了大量非饱和土的抗剪强度理论公式,应用较广的是Fredlund基于Mohr-Coulumn准则推导出的双应力状态变量理论公式[6]:
τf=c′+(σ-ua)tanφ′+(ua-uw)tan(φb)
(6)
式中:τf为非饱和土抗剪强度;c′为有效粘聚力;φ′为有效内摩擦角;ua为孔隙气压力;uw为孔隙水压力;(σ-ua)为净法向应力;(ua-uw)为基质吸力;φb为受基质吸力影响的摩擦角,tan(φb)表示基质吸力对应抗剪强度曲线的斜率。
根据Fredlund强度理论[5],抗剪强度受净法向应力和基质吸力影响。在有限元分析中常常将孔压气压力设置为零,故非饱和土强度主要受基质吸力的影响,获得基质吸力是研究非饱和土强度及边坡稳定性的关键。
1.4 强度折减方法
本文应用强度折减法计算降雨入渗后边坡的稳定系数,通过人为假定不同折减系数对抗剪强度指标进行折减,削弱土体的抗剪强度使单元应力达到屈服或超出屈服面,边坡产生塑性变形;当其内部形成连续塑性贯通面或特征部位产生突变位移,表征边坡失稳破坏。
cm=c/Fs
φm=arctan(tanφ/Fs)
(7)
式中:Fs为强度折减系数;c、φ为实际抗剪强度指标;cm、φm为人为折减后的抗剪强度指标。
实现方法:提取边坡降雨入渗分析后单元节点的孔隙水压力,转换为荷载施加到节点上,定义折减系数为场变量,实现边坡的强度折减,计算边坡稳定系数。
2 有限元计算模型
2.1 土水特征曲线模型
根据非饱和土力学[5]:非饱和土的基质吸力是伴随土体含水量变化而变化的,可应用土水特征曲线表征含水量与基质吸力的函数关系。本文应用滤纸法测量膨胀土的基质吸力。滤纸法将滤纸作为测量传感器,将滤纸直接接触土样,通过测量滤纸的平衡含水量结合滤纸的率定曲线计算出土体的基质吸力[7]。
首先配置不同含水率的膨胀土样,将其制备成标准环刀试样(同一含水率两组试样),选择国产“双圈”牌NO.203滤纸与环刀试样直接接触,恒温环境静置10天,测量滤纸含水量及土试样含水率,应用滤纸的率定公式[8](公式8)计算出不同含水率对应基质吸力值(图1实测值点)。
lg(hm)=-0.076wfp+5.493,wfp≤47%
lg(hm)=-0.012wfp+2.470,wfp>47
(8)
基于滤纸法试样数据,结合Fredlund-Xing[5]数学模型经验公式(公式9)分析土体体积含水率与基质吸力的相关关系,应用Matlab程序计算出Fredlund-Xing模型的参数(表1),得到体积含水率与基质吸力的拟合公式,绘制膨胀土的土水特征曲线(图1拟合曲线)。
(9)
式中:θ为非饱和土的体积含水率;θs为饱和体积含水率;h为基质吸力;hr是与土样的残余含水率θr的基质吸力相关的量;α、m、n为与土水特征曲线形态相关参数(表1)。

表1 Fredlund-Xing模型参数

图1 膨胀土土水特征曲线
2.2 边坡数值模型
边坡为非饱和膨胀土边坡,有限元模型如图2所示。
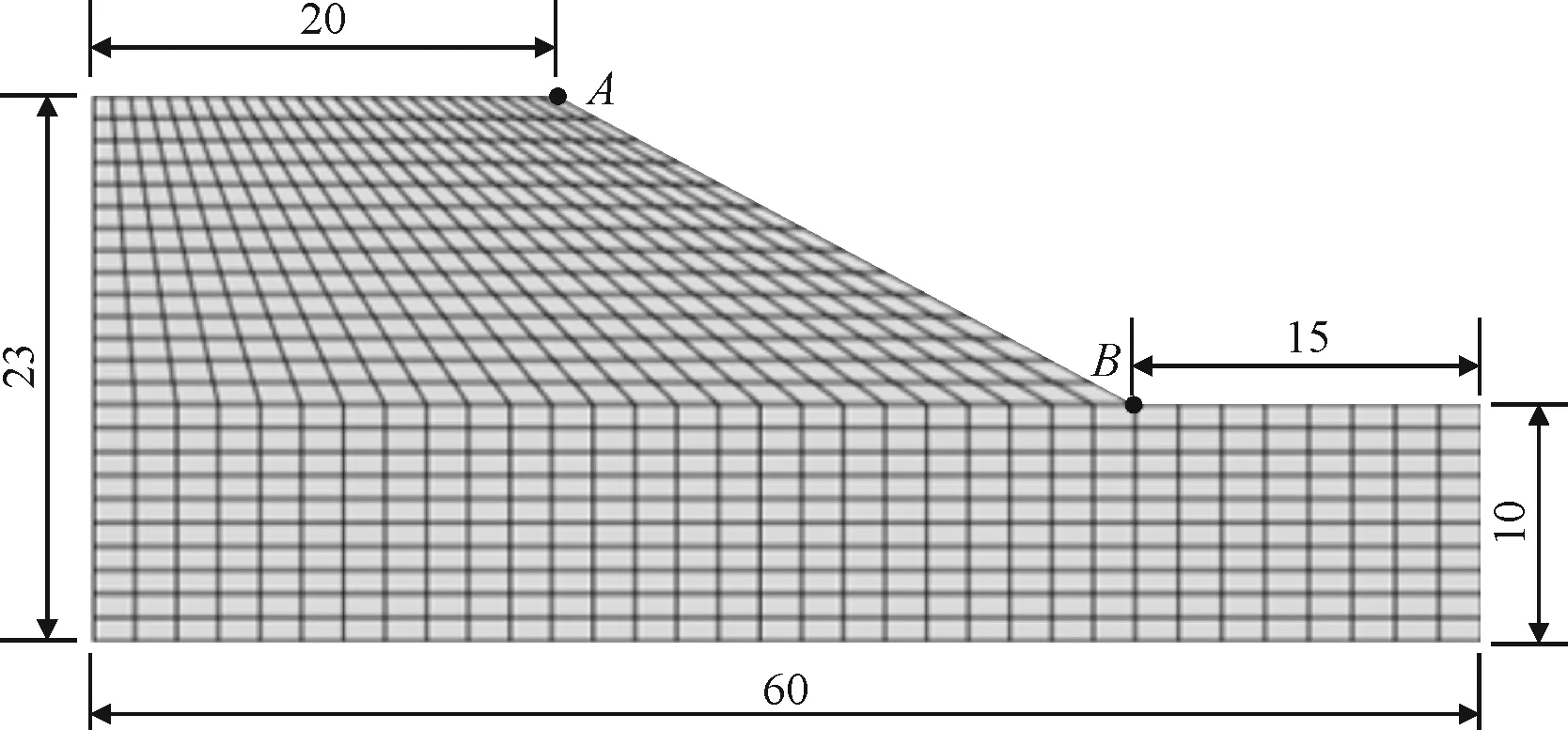
图2 非饱和膨胀土边坡模型示意(单位:m)
初始条件:底面设置为双向(水平向、竖向)约束边界,侧面设置为水平向约束边界,其余为自由边界;左侧边界地下水位为10m,右侧边界地下水位为8m,边坡顶面、临空面及地表设置为降雨入渗边界。
降雨条件:降雨强度为0.01m/h,降雨历时为24h,降雨全部入渗。土体材料为理想弹塑性模型,遵循Mohr-Column强度准则。具体材料参数如表2。

表2 土体材料参数
3 计算结果分析
3.1 渗流场分析
降雨入渗非饱和膨胀土边坡后,土体含水率增加,孔隙水压力发生显著变化。图3为边坡降雨前后孔隙水压力分布云图。降雨前,边坡初始水位以下为饱和区,土体孔压为正;初始水位以上为非饱和区,土体孔压为负由水位面向坡顶线性减小;降雨24h后,边坡非饱和区逐渐减小,饱和区逐渐扩大发展至整个边坡,地下水位发生显著抬升。取边坡顶部(A点)和坡脚(B点)探究非饱和土孔隙水压力变化规律。图4为降雨过程边坡孔隙水压力变化曲线:降雨初期,边坡表层土体孔压迅速增加,雨水向边坡内部渗流,降雨5h左右,坡脚孔压为零土体率先达到饱和,表明雨水首先在坡脚处汇集;伴随降雨持续土体孔压也持续递增,坡脚土体孔压变化率大于坡顶,降雨中后期,坡脚土体达到最大孔压值,受土体强度降低变形增大影响,土体孔压开始减小并逐渐趋于稳定;坡顶土体孔压持续增加,降雨20h左右,坡顶孔压为零,土体达到饱和,孔压逐渐趋于稳定。

图3 降雨前后孔压分布云图
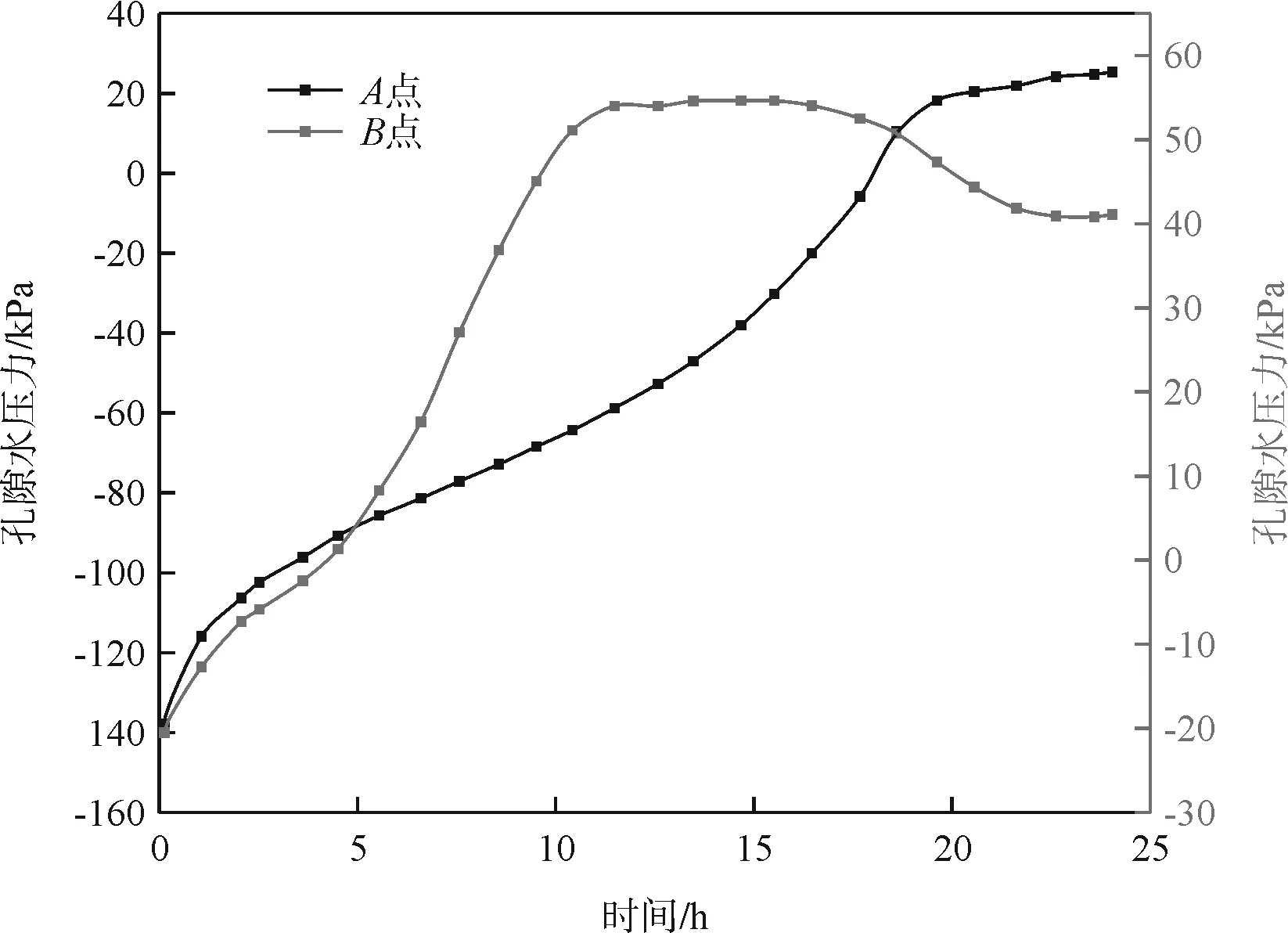
图4 降雨过程边坡孔压曲线
3.2 位移场分析
取坡脚(B点)土体为位移监测对象。降雨过程土体位移曲线如图5所示,土体位移伴随降雨历时递增,土体位移变化率由小到大缓慢增加。根据土体位移曲线斜率变化规律,以降雨12h为节点将位移曲线划分为稳定小变形阶段与非稳定大变形阶段:(1)稳定小变形阶段:曲线较平缓斜率小,土体位移很小,伴随降雨时间增长变形缓慢递增,以小变形为主;(2)非稳定大变形阶段:曲线较陡斜率较大,土体位移迅速增加,位移变化率较大,土体发生不可逆大变形,降雨结束后边坡总体位移较大,水平位移大于竖向位移,表明降雨引发了边坡失稳破坏。结合降雨过程土体总体位移矢量图(图6)分析,边坡内部发育圆弧形滑动面,土体顺滑动面向外滑移,以水平位移为主,上部土体率先产生大变形,推移中下部土体向坡外移动,边坡具备典型推移式滑坡特征。

图5 降雨过程土体位移曲线

图6 降雨结束土体总位移矢量
3.3 稳定性分析
降雨过程,土体强度受基质吸力变化而降低,边坡的稳定系数逐渐减小,稳定性降低。图7为膨胀土边坡的塑性面发展示意图。降雨初期坡脚土体率先达到饱和,土体基质吸力迅速减小,强度减小至较小值,坡脚处首先产生塑性变形见图7(a),稳定系数为1.25;伴随降雨持续,边坡饱和区扩大而地下水位抬升,边坡后缘水位高于坡脚水位,内部雨水以向坡脚渗流为主,坡脚土体受水平向渗流力作用,有效应力逐渐减小,塑性变性由坡脚逐渐向内部顶部发展,降雨12h左右,塑性面发展至坡顶,边坡内部形成圆弧形贯通面见图7(b),稳定系数为0.994,边坡开始失稳滑动;降雨结束后,边坡整体失稳破坏,发生推移式滑坡,滑面形式为中心圆,稳定系数为0.845,见图7(c)。

(a)降雨5h
4 结论
(1)本文应用滤纸法实验,结合Fredlund-Xing数学经验公式,推导出非饱和膨胀土的土水特征曲线模型,绘制了土水特征曲线,可供实际工程参考。
(2)持续降雨过程,雨水首先在坡脚处汇集,再逐渐向边坡内部入渗。边坡失稳的主因是地下水位差异抬升,边坡内部雨水向坡脚渗流,受水平向渗流力作用土体有效应力减小;渗流区域土体软化,基质吸力减小而强度降低,内部发育圆弧形滑动面,土质边坡产生推移式滑动。
