某地铁转换层上盖结构的弹塑性时程分析

简 立

(西南交通大学土木工程学院，四川成都 610031)

1 工程概况

本工程为地铁车辆基地上盖商业综合体。综合楼建筑总面积约40 650 m2，建筑总高度39.5 m，主体采用钢筋混凝土框架结构。该建筑底部为东岗车辆段运用库，位于地下，功能为地铁车辆检修和停车，运用库为一层，辅助边跨局部两层，层高共11.5 m。地上结构为住宅或商业综合体，共7层，层高4 m。为了满足建筑使用功能的要求，该结构在9.5 m标高处设置了转换层，除此之外，结构整体布置非常规则，且楼层顶部无突出部位。

本工程建筑设计使用年限为50年，抗震设防类别为丙类，设防烈度为8度，设计基本地震加速度0.2g，设计地震分组为第三组，场地类别为Ⅱ类，场地特征周期0.4 s，结构阻尼比为0.05。该结构的基本模型和平面布置见图1。

(a)左视

2 弹塑性动力分析模型的建立

为判断结构是否满足抗震性能目标，本文采用PERFORM-3D对结构进行弹塑性时程分析。计算时，考虑材料非线性、P-Δ效应以及模态阻尼。

2.1 本构形式

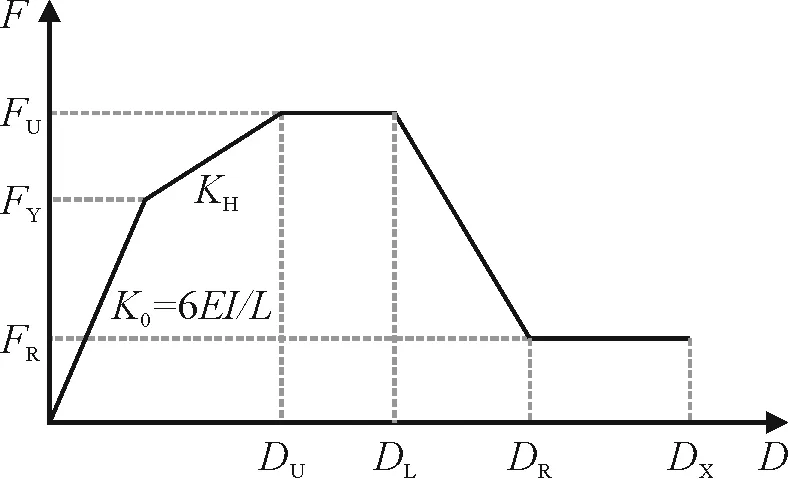
模型涉及单元均选择三折线型骨架曲线，并考虑强度损失和刚度退化。由于PERFORM-3D中的F-D(广义力-广义位移)曲线和FEMA356中的F-D曲线参数互相对应[1]，因此结合FEMA356中给出的模型具体参数[2]，即可确定模型单元的本构曲线，如图2所示。

(a)PERFORM-3D

2.2 单元模型

PERFORM-3D中有很多种模拟弹塑性梁的办法，例如弦转角模型、塑性铰模型、塑性区模型以及纤维模型。其中，弦转角模型用起来非常方便，且FEMA356对此模型模拟钢构件和混凝土构件都作出了详细的定义，因此本文采用该模型来模拟结构的梁单元。弦转角模型由两个具有非线性性质的FEMA梁构件组成，每一个FEMA梁构件被分成塑性铰和弹性段两部分(图3)。柱单元模型设置与梁单元一致，在此不作赘述。

图3 弦转角模型的实现

2.3 截面分析

本论文采用XTRACT截面计算软件，对结构中的各构件进行截面分析，获得混凝土构件截面的弯矩-曲率关系曲线及轴力-弯矩关系曲线，从而确定梁柱构件的相关参数，完成截面的定义和赋予。图4所示为结构中的型钢混凝土梁柱构件的截面网格划分以及计算结果示例。

(a)型钢混凝土梁示例

2.4 模态分析

采用SAP2000和PERFORM-3D分别对结构模型进行模态分析，计算得到了模型前三阶的模态、周期以及结构总质量，如表1所示。

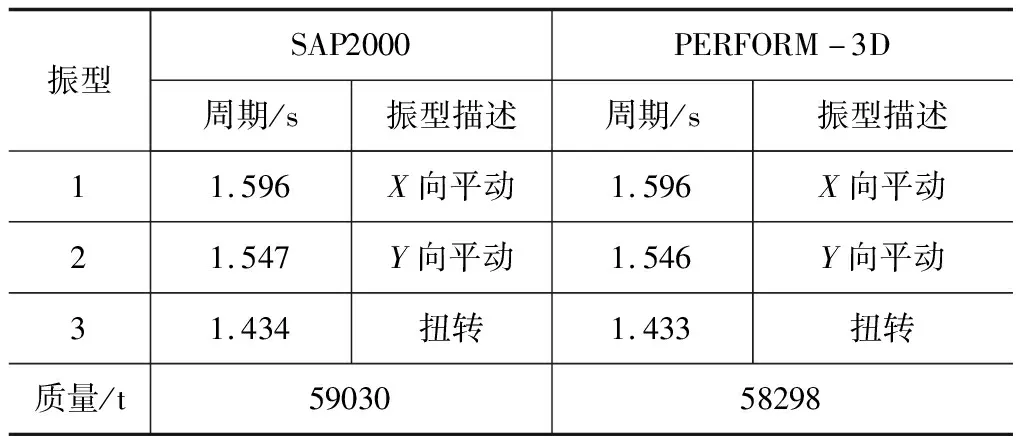
表1 结构振型、周期、质量对比

对比表中数据可知，两个软件计算出的周期、模态以及质量几乎一致，因此，可以认为模型准确度较高，能够被用于完成弹塑性时程分析。

2.5 地震波选取

根据(GB 50011-2010)《建筑抗震设计规范》5.1.4的规定，建筑结构的地震影响系数应根据烈度、场地类别、设计地震分组和结构自振周期以及阻尼比确定，并且在计算罕遇地震作用时，特征周期应增加0.05 s。据此，选择了两条天然波TH2TG055、TH3TG055和一条人工波RH3TG055，采用三组两向地震波输入，每组进行两个主方向的地震动力时程分析，总计6个工况，水平加速度峰值为400 cm/s2，结构阻尼比取0.05。各地震波反应谱和设计反应谱曲线对比见图5。

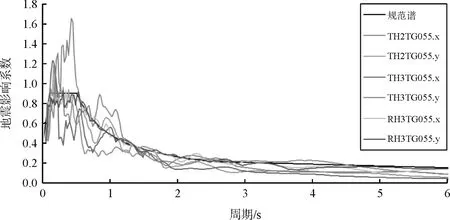
图5 各组地震波反应谱和设计反应谱对比

3 时程分析结果

3.1 顶点位移时程

目标点选取结构顶层上的中心点。在六组地震波激励下的顶点位移时程反应见图6，位移值是顶点与零点标高点之间的相对位移值。

各工况顶点位移时程中顶点位移的最大值如表2所示。

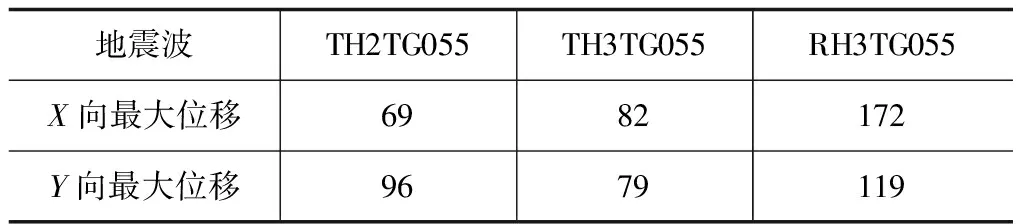
表2 顶点位移最大值 mm

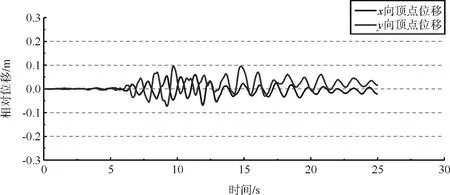
(a)地震波TH2TG055激励下的顶点位移时程

在考虑几何非线性的情况下，结构在罕遇地震作用下的的最大顶点位移为172 mm，并且基本保持直立，满足“大震不倒”的设防要求。

3.2 层间位移角沿高度分布

本文用到的层间位移角是楼层平面中心点的水平相对位移与层高的比值。罕遇地震下，结构在整个时程分析中各楼层的最大层间位移角分布见下图7。从图中可以看出，结构的层间位移角最大值和拐点均出现在第5层附近，这是由于该结构在第五层的竖向构件存在变截面，即此处结构的竖向刚度发生了变化，所以该结果是合理的。

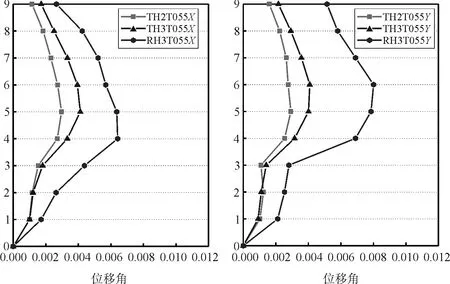
图7 X轴向、Y轴向层间位移角沿楼层分布

在罕遇水准的三条地震波输入下，X向层间位移角最大值1/156，发生在第4层，Y向层间位移角最大值1/125，发生在第6层，均满足抗震规范1/50的限值要求。根据GB 50011-2010《建筑抗震设计规范》中新纳入的建筑抗震性能化设计概念[3]，配合使用(1990)建抗字第377号《建筑地震破坏等级划分标准》中对地震破坏分级和地震直接经济损失的估计办法，可以通过弹塑性层间位移角来评价结构的损伤状态(表3)。

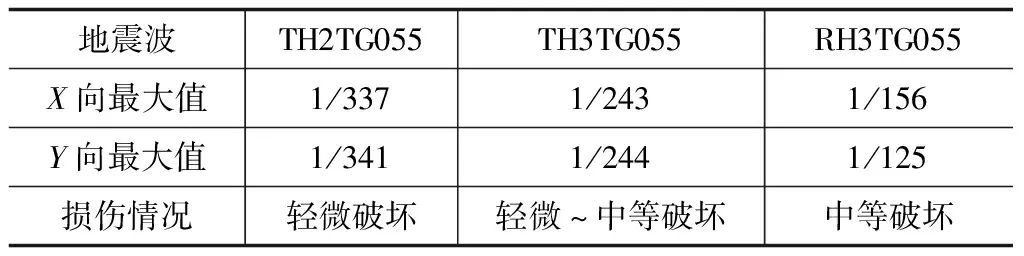
表3 层间位移角最大值和结构损伤状态

从表3可以看出，在多条罕遇水准地震波作用下，结构达到了中等破坏，这种损伤状态对应于多数承重构件轻微裂缝(或残余变形)，部分明显裂缝(或残余变形)；个别非承重构件严重破坏。需要一般修理，采取安全措施后可适当使用[4]。

3.3 层剪力沿高度分布

在PERFORM-3D中定义的层剪力为各楼层底部所有竖向构件所受剪力之和，取整个时程分析中的最大值，分为X轴向剪力分量和Y轴向剪力分量。结构每层的最大层剪力沿楼层分布如图8所示。

(a)X向剪力 (b)Y向剪力

结构X、Y轴向每组地震波下层间剪力最大值都出现在底层，罗列于表4：

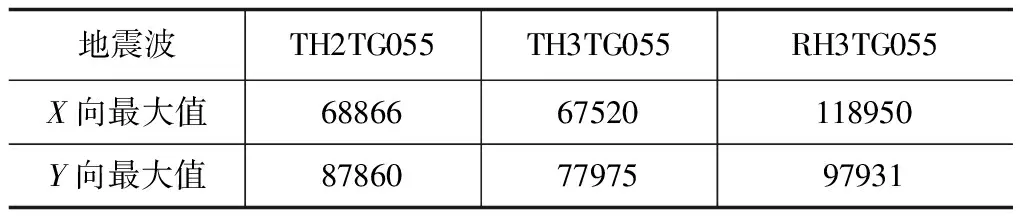
表4 各组地震下的最大层剪力 kN

结构X轴向层剪力最大值118 950 kN，最小值13 615 kN，，均值48 824 kN；结构Y轴向层剪力最大值97 931 kN，最小值17 681 kN，均值50 301 kN。

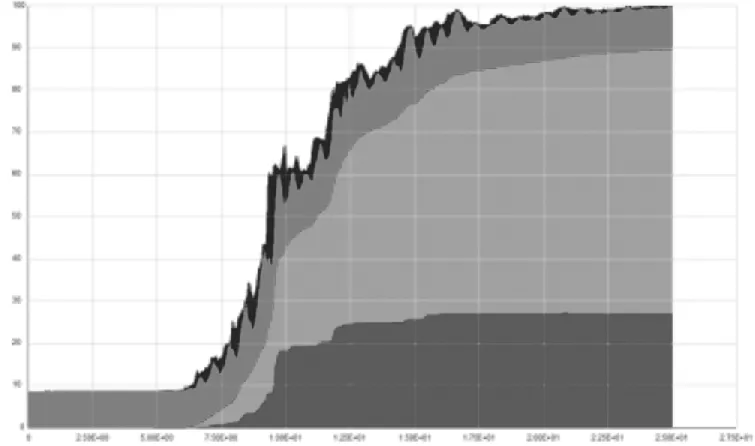
3.4 结构耗能分析

结构耗能图9中，X轴为时间轴，Y轴为耗能百分比。

从图9中可以看出，在罕遇地震下该结构的塑性耗能最大约53 %(RH3TG055X)，最小约22 %(TH3TG055X)。在相同峰值加速度的地震作用下，结构所处的非线性状态差异极大，表明峰值加速度大小不是影响结构响应的最重要因素，地面运动中的频谱信息才对结构响应起控制作用[5]。

除了构件的塑性耗能外，大部分能量都是由于阻尼的作用而消耗的，阻尼耗能在结构总能量耗散中占的比重较大，因此阻尼的设置对结构的响应有较大的影响。阻尼设置过大，结果会偏不安全，使结构响应偏小，反之评价则会趋于保守。

另外，从各个构件的耗能对结构整体耗能的贡献来看，框架梁的耗能几乎占总耗能的全部，这说明结构中进入非线性的构件基本全是框架梁，而框架柱几乎没有耗能贡献，本结构较好地体现了强柱弱梁的设计理念。

4 结论

通过对此转换层结构进行弹塑性时程分析，得出以下结论：

(1)在考虑几何非线性的情况下，结构在罕遇地震作用下的最大顶点位移为172 mm，X轴向层剪力最大值118 950 kN，

(a)TH2TG055X

Y轴向层剪力最大值97 931 kN，基本保持直立，满足“大震不倒”的设防要求。

(2)罕遇地震的作用下，该结构X向层间位移角最大值1/156，Y向层间位移角最大值1/125，均满足抗震规范1/50的限值要求，且均出现在第5层附近，这是由于该结构在第五层的竖向构件存在变截面，竖向刚度发生了改变，所以结果合理。

(3)在多条罕遇水准地震波作用下，结构达到了中等破坏，这种损伤状态对应于多数承重构件轻微裂缝(或残余变形)，部分明显裂缝(或残余变形)；个别非承重构件严重破坏。需要一般修理，采取安全措施后可适当使用。

(4)峰值加速度大小不是影响结构响应的最重要因素，地面运动中的频谱信息才对结构响应起控制作用。此外，阻尼的设置对结构的响应也有较大的影响。