边坡安全系数预测的机器学习算法比较研究
2020-07-18刘毅聪刘祚秋
王 杰,刘毅聪,刘祚秋
(中山大学航空航天学院应用力学与工程系 广州510006)
诸多因素综合影响下的边坡,具有复杂的变形破坏机理和模式。影响因素的显著特点是数据的多变性、不完备性以及参数的不确定性。目前,分析边坡变形破坏机理及评价其稳定性的方法主要为极限平衡和数值分析方法。这些精确的分析方法在很多情况下是不适宜的。一方面,大多数的工程只需对边坡进行广义的危险性识别,对边坡作出快速准确的判断;另一方面,由于参数的不确定性和不完备性,“精确”分析方法在表达边坡系统各组成部分之间的非线性关系上有局限性。因此,找到一种合适的方法进行边坡稳定预测具有重大意义[1]。
胡杰等人[2]建立基于信息增益率作为切分特征选取的参数,且进行剪枝操作的C4.5决策树预测土质边坡的稳定性,该研究的训练样本数为70,测试样本数为10,得到的模型在测试集上的正确率为90%,具有较好的预测性能;胡添翼等人[3]建立随机森林模型预测边坡稳定性,该研究在样本划分上分别采用随机划分与交叉验证的方法,得到的模型在测试集上具有较好的预测性能,而且通过改变基学习器数进行的实验,可得出当基学习器的数目为500时,模型在该研究的数据中具有较好的准确性;姚玮等人[4]利用30个训练样本建立随机森林模型预测边坡稳定性,用另外12个样本测试测试模型的性能,该研究的随机森林基学习器数设为500。
综上所述,机器学习算法具有较强的非线性动态处理能力。无需知道数据的分布形式和变量之间的关系,可实现高度非线性映射关系。其较强的学习、记忆、存储、计算能力以及容错特性,适用于从实例样本中提取特征、获得知识,并可使用残缺不全的或模糊随机的信息进行不确定性推理。使用的机器学习算法主要有逻辑回归、决策树、支持向量机、多层感知机,但是评价模型性能的指标不一。本文使用的算法有Lasso 回归、Ridge 回归、决策树、XGboost,评价指标选用均方根误差。本文以相同的训练样本和测试样本分别建立模型,其中训练样本来自文献[5-7],测试样本来源于文献[8],通过比较各样本的预测值与真实值的差距、计算预测值与真实值的均方根误差评价各模型的预测性能,并且对各模型进行对比分析。
1 机器学习算法概述
机器学习(Machine Learning,ML)是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。
1.1 Lasso回归与岭回归(Ridge回归)
Lasso 回归[9,10]与岭回归的损失函数以多元线性回归损失函数为基础,分别引入一个L1 正则项与L2正则项,是对多元线性回归损模型的改进,Lasso 回归与岭回归的损失函数分别如式⑴与⑵所示:

式中:C为惩罚项系数。
1.2 决策树算法
决策树是基于信息论的一种机器学习算法,该算法关键的问题是对切分特征及其切分点的选取;为了防止决策树过拟合,可设置决策树停止分裂的条件以及对决策树进行剪枝。
决策树的生成可分为以下步骤:
step1:初始时,所有样本点集中在根节点,进入step2;
step2:根据信息增益或者Gini 系数,在所有的特征中选取一个特征对节点进行分割,进入step3;
step3:由父节点可生成若干子节点,对每一个子节点进行判断,如果满足停止分裂的条件,进入step4;否则,进入step2,继续分裂;
step4:叶子节点中比例最大的类别作为输出。
从决策树生成的步骤可得,决策树构建的关键问题是分裂特征及其分割点的选取与停止分裂条件的设定[11]。
1.3 Xgboost算法(eXtreme Gradient Boosting)
Xgboost 算法是在GBDT 算法基础上改进优化得到的算法。
Xgboost模型表达式:
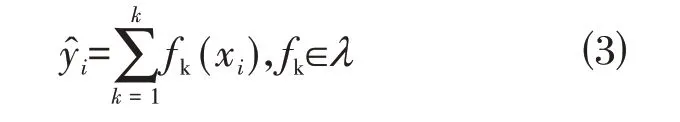
式中:fk(x)为第k 个CART(Classification and Regression Trees,分类回归树)损失函数:

式中:第一部分为预测值与真实值的损失,第二部分为fk的正则项,该项用于惩罚fk的复杂程度。
第t轮迭代后的损失函数:

式中:常数项为前(t-1)个CART的复杂度。
通过优化损失函数,可得叶子节点的最佳值与对应的损失函数的值:

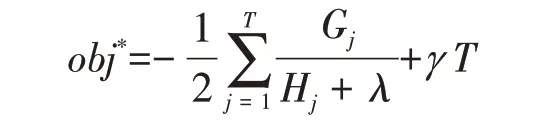
CART节点的生成:
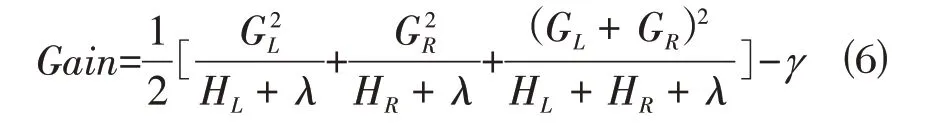
式中:Gain 为父节点的obj*减去左右两个子节点的obj*之和,即节点切分后obj*的下降值,Gain 值越大,且大于设定的临界值γ,则切分的效果越好。
2 特征与参数选取及模型构建
边坡稳定的影响因素主要有重度、内聚力、摩擦角、边坡角、边坡高度、孔隙压力比、地下水等,本文选用的特征有重度、内聚力、摩擦角、边坡角、边坡高度、孔隙压力比,预测边坡的安全系数。本研究在建模之前对特征的分布与特征与目标的关系进行分析,然后以106 个边坡实例样本为训练样本,以29 个边坡实例样本为测试样本,分别建立Lasso回归模型、Ridge回归模型、决策树模型、Xgboost模型预测边坡的安全系数。
2.1 Lasso回归模型
Lasso回归模型在损失函数中引入L1正则项并利用梯度下降法优化损失函数,所以要对量纲有较大差别的特征取值进行标准化处理[10]。
在建立Lasso 回归模型过程中,需要对特征取值进行处理,然后选取合适的模型参数:
2.1.1 缺失值处理
特征“孔隙压力比”的缺失值比例为0.03,缺失值的数量较少,可以用“孔隙压力比”的均值填充缺失值。
2.1.2 标准化
由于各特征取值的量纲有较大差别,需要对特征进行标准化,本研究使用z-score标准化,公式如下:

式中:x为原值;x'为经过变换后的取值;μ为特征取值的均值;σ 为特征取值的标准差。
经过z-score 标准化后,特征的分布变为以0 为均值,以1为标准差。
2.1.3 选取正则项系数
通过正则项系数与均方根误差的关系曲线,选取均方根误差最小对应的正则项系数,如图1所示。根据正则项系数与均方根误差的关系曲线,选取正则项系数为0.02。
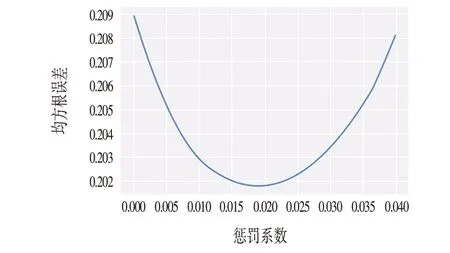
图1 惩罚系数与均方根误差的关系Fig.1 Relationship between Penalty Coefficient and Root Mean Square Error
2.2 Ridge回归模型
Ridge 回归模型在多元线性回归模型的基础上在损失函数中引入L2 正则项,Ridge 回归可通过直接法或者梯度下降法求解参数[12]。
在建立Ridge 回归模型过程中,需要对特征取值进行处理,然后选取合适的参数:
⑴缺失值处理:特征“孔隙压力比”的缺失值比例为0.03,缺失值的数量较少,可以用“孔隙压力比”的均值填充缺失值;
⑵标准化:由于各特征取值的量纲有较大差别,需要对特征进行标准化,本文使用z-score标准化;
⑶选取正则项系数:通过正则项系数与均方根误差的关系曲线,选取均方根误差最小对应的正则项系数,根据正则项系数与均方根误差的关系曲线,选取正则项系数为10.0。
2.3 决策树模型
本文选用决策树中的回归树预测边坡安全系数;决策树模型是非线性模型,形式为二叉树;决策树模型是概率模型,关注的是特征的分布和特征与目标之间的条件概率,不需要通过优化损失函数进行参数估计,所以可不对数值型取值进行标准化处理;决策树模型建立后,可生成直观的决策过程[13]。
在建模过程中,首先对特征缺失值进行处理,然后选取合适的模型参数。
⑴缺失值处理:特征“孔隙压力比”的缺失值比例为0.03,缺失值的数量较少,可以用“孔隙压力比”的均值填充缺失值;
⑵参数选取:决策树节点质量评价标准:回归树中节点质量以误差评价,本研究中节点质量以均方差表示;
决策树最大层数与叶子节点最小样本数:决策树的最大层数与叶子节点最小样本数为决策树生长停止的条件,可降低决策树模型过拟合的风险,本文中决策树最大层数设为5,叶子节点最小样本数设为1。
2.4 Xgboost模型
在本文中,Xgboost 模型以回归树为基学习器,通过不断迭代生成集成模型,Xgboost 模型可以根据特征被用于决策树生长的次数来计算特征重要性,特征被用于决策树生长的次数越多,则特征越重要[14]。
建立Xgboost模型:
2.4.1 选用模型参数
⑴学习率:学习率为模型迭代更新过程中的收缩步长,可降低模型过拟合风险,一般情况下,学习率随着模型迭代次数的增大而减小,本文的学习率选用0.005;
⑵最大层数:最大层数为Xgboost 模型基学习器的生长停止条件,在达到最大层数后,基学习器开始剪枝,可降低模型的过拟合风险,本文的最大层数选用8;
⑶特征与样本的抽取比例:在训练基学习器时,可选用训练样本中部分特征与样本进行训练,可降低模型的过拟合风险,本文的特征抽取比例为0.9,样本抽取比例为1;
⑷模型在迭代过程中的误差评价指标:误差评价指标选用均方根误差。
2.4.2 迭代过程
模型在训练集上的误差随着迭代次数的增大而减小,此过程说明模型的拟合能力随着迭代次数的增大不断增强;模型在测试集上的误差随着迭代次数的增大先减小后增大,此过程说明模型的泛化能力随着迭代次数的增强先增大后减弱;当模型的拟合能力增强而泛化能力减弱时,则模型出现过拟合的问题;为了解决这个问题,可设置迭代提前停止的步数,当模型连续迭代了设置的步数而在测试集的误差没有下降时,模型停止迭代。
模型在训练集与测试集的误差随迭代次数的变化如图2所示。
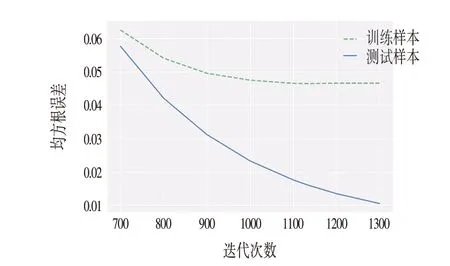
图2 迭代次数与均方根误差的关系Fig.2 The Relationship between the Number of Iterations and Root Mean Square Error
当模型迭代到1 135 步时,模型在测试集上的均方根误差达到最小值,其值为0.046。
3 预测结果与对比分析
3.1 预测结果
模型对测试样本的预测结果如表1、表2、图3所示。Xgboost 模型可根据特征被选作切分特征的次数得到特征的重要性,如表3所示。
特征重要性的取值为特征被选为切分特征次数的相对值,从表3 可得,重要的前3 个特征为”重度”、“内聚力”、“边坡高度”,在实际工程中,可以重点关注这3个影响因素。
3.2 模型对比及分析
根据以上预测结果对各模型预测性能进行对比分析。由于各模型选用的特征、训练样本、和测试样本都相同,所以各模型性能就代表了在边坡安全系数预测这个问题上各自算法的性能。
⑴Lasso 回归模型与Ridge 回归模型的最大误差与均方根误差较大,预测值曲线与真实值曲线偏离较大,超出实际工程中的可接受范围;决策树模型的最大误差较大,均方根误差在实际工程中可接受,预测值曲线与真实值曲线有一定的偏离,预测效果一般;Xgboost 模型的最大误差与均方根误差在实际工程可接受范围内,预测值曲线与真实值曲线比较吻合,预测效果较好;

表1 模型预测结果Tab.1 Model Predictions
⑵Lasso回归模型与Ridge回归模型
Lasso回归模型是损失函数正则项为L1正则项的多元线性回归模型,Ridge 回归模型是损失函数正则项为L2 正则项的多元线性回归模型。在本研究中两者的预测结果相近且预测结果的误差较大,多元线性回归模型对本研究数据的适应性较差。
⑶决策树模型与Lasso回归模型、Ridge回归模型
决策树模型是非线性模型,在特征与目标存在非线性关系的数据中比线性模型具有优越性。在本研究中,决策树模型的最大误差与均方根误差小于Lasso 回归模型与Ridge 回归模型,其预测值曲线与真实值曲线比较接近,具有更好的预测性能。
⑷Xgboost模型与决策树模型

表2 模型对比分析Tab.2 Model Comparison Analysis

图3 各模型预测值与真实值的比较Fig.3 Comparison of Predicted and True Values of Each Model

表3 特征重要性Tab.3 Significance of Characteristics
Xgboost 模型是基于决策树的集成模型,在其迭代过程中可根据之前决策树模型的错误形成新的决策树,然后把所有决策树通过加权求和得到集成模型,其预测结果比单个决策树更加全面;Xgboost 模型有更多的叶子节点,有更多的输出值,取值比单个决策树更精细。本文中,Xgboost 模型的最大误差与均方根误差小于决策树模型,其预测值曲线与真实值曲线更加接近,具有更好的预测性能;
综上,本文中模型的预测性能由高到低的排序为:Xgboost 模型>决策树模型>Lasso 回归模型>Ridge回归模型。
4 结论
本文以均方根误差评价模型的预测性能,从而探究模型的非线性与集成性对预测性能的影响;本文中,算法预测性能从高到低的排序为:Xgboost 算法>决策树算法>Lasso回归算法>Ridge回归算法,非线性集成模型对本数据样本有较好的适应性,Xgboost 模型较其他模型更为精确,能分析边坡的稳定性,有一定的工程参考和实用价值;由Xgboost 模型可得,重要的前3 个特征为”重度”、“内聚力”、“边坡高度”,在实际工程中,可以重点关注这3个影响因素。
