基于量子自组织网络的水淹层识别方法
2020-07-18卢爱平李建平李盼池范友贵
卢爱平, 李建平, 李盼池, 范友贵
(1. 东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318; 2. 中国石油吉林油田公司, 吉林 松原 138000)
水淹层识别是油田开发中后期油藏测井解释的一个主要问题, 目前常用的方法有两类: 传统的地质、 化学和物理测井分析方法和人工智能分析方法. 由于受实验室设备、 地域和样品数量的限制, 第一种方法存在较大的局限性. 采用智能计算技术解决水淹层识别方法很多, 其中基于神经网络的方法主要包括经典神经网络方法[1-3]、 模糊神经网络方法[4-5]、 支持向量机方法[6-7]和过程神经网络方法[8-9]. 但这些方法都不同程度地存在缺陷, 如神经网络易陷入局部极小值, 支持向量机的核函数参数不易确定等. 因此探索新的计算方式, 采用新的网络模型解决水淹层识别问题有一定的应用价值.
量子计算[10-11]、 量子信息处理[12]、 量子机器学习[13-17]已成为目前该领域的研究热点. 尽管这些量子新模型借助量子计算的并行性可显著提高计算效率, 但其都是面向量子计算机的, 在传统计算机上无法执行. 量子衍生计算通过借鉴量子计算的某些机制改进经典算法的性能, 已获得了成功应用[18-20], 但对量子衍生神经网络应用于水淹层识别问题的量子衍生模型研究目前报道较少.
量子自组织网络(quantum self-organizing network, QSON)是量子计算和自组织网络相融合的新模型[21], 其采用量子计算机制构造竞争获胜规则, 设计理念面向传统计算机, 本质上是借助量子计算的某些机制(量子比特的球面描述、 绕轴旋转、 测量等)提升经典方法的性能. 本文提出一种基于QSON的水淹层识别方法, 并对辽河油田某区块的实际测井资料数据进行仿真实验, 利用QSON对数据处理后的结果进行分析. 结果表明, 该方法的水淹层识别精度明显高于同类对比方法.
1 量子自组织网络模型
本文采用基于Bloch球面旋转的量子自组织网络模型[21], 其输入和竞争层权值均采用Bloch球面描述的量子比特. 以竞争层C=m2个节点为例, 网络模型如图1所示.
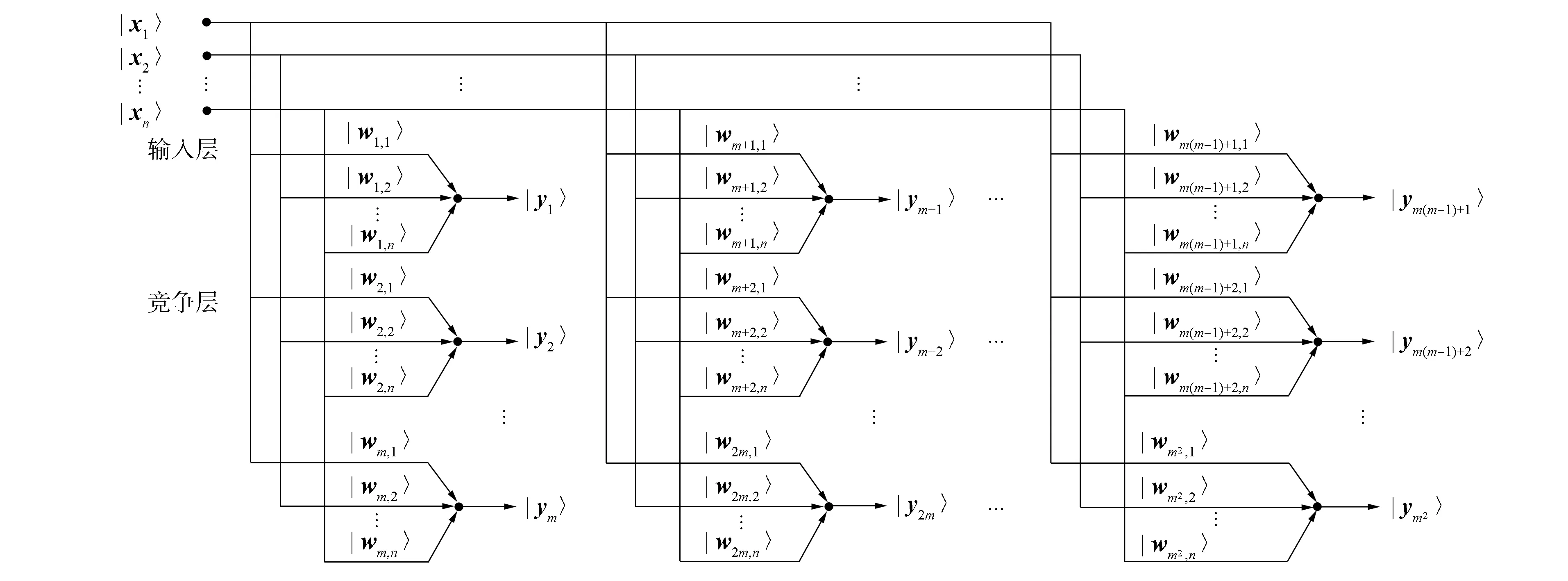
图1 量子自组织网络模型
根据量子计算原理, 量子比特|φ〉的Bloch球面坐标(x,y,z)可通过投影测量获得, 测量方法采用Pauli矩阵实现, 表示为
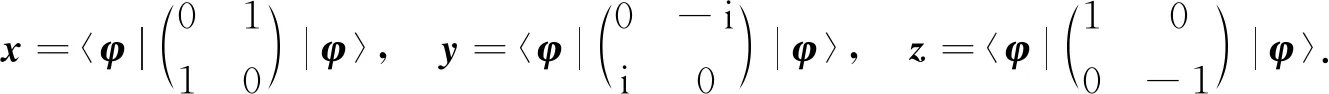
(1)
令输入为|X〉=(|x1〉,…,|xn〉)T, 竞争层第j个节点权值为|Wj〉=(|wj1〉,…,|wjn〉)T. |xi〉和|wji〉经测量后的Bloch坐标分别为|xi〉=(xix,xiy,xiz)T和|wji〉=(wjix,wjiy,wjiz)T. 根据文献[21], 样本|X〉与权值|Wj〉间的距离, 即竞争层第j个节点的输出为

(2)
1.1 样本量子态描述
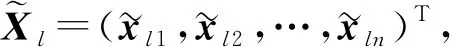
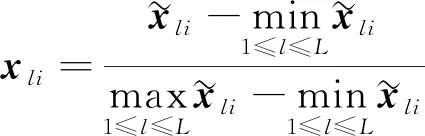
(3)
将样本归一化处理为Xl=(xl1,xl2,…,xln)T. 利用
θl=(πxl1,πxl2,…,πxln)T=(θl1,θl2,…,θln)T,
(4)
φl=(2πxl1,2πxl2,…,2πxln)T=(φl1,φl2,…,φln)T
(5)
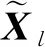
|Xl〉=(|xl1〉,|xl2〉,…,|xln〉)T,
(6)
其中
1.2 竞争学习规则
令竞争层第j(j=1,2,…,C)个节点的权值量子比特|Wj〉为
|Wj〉=(|wj1〉,|wj2〉,…,|wjn〉)T,
(7)
对第l个样本|Xl〉=(|xl1〉,|xl2〉,…,|xln〉)T, 由式(1),(2)可知, 其与|Wj〉之间的距离为
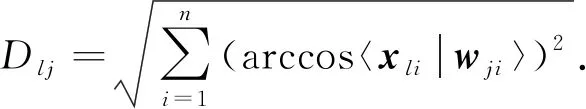
(8)
令竞争规则为具有最小距离的节点获胜, 则获胜节点j*满足
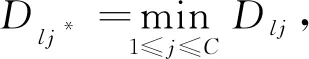
(9)
其中C为竞争层节点数.
1.3 网络聚类算法
与经典自组织网络相同, 量子自组织网络也属于无监督聚类模型, 用于解决预先未知类数的聚类. 聚类算法完全采用无监督方式进行, 聚类过程描述如下.
步骤1) 样本量子态. 按式(3)~(6)完成样本量子态描述, 按式(1)进行样本量子态的投影测量, 以获得每个样本每维数据对应的3个Bloch坐标值.
步骤2) 网络权值初始化. 权值初始化为
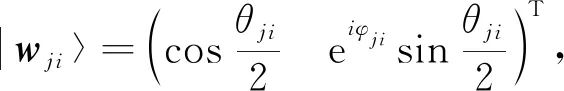
(10)
其中θji=π·rnd,φji=2π·rnd,j=1,2,…,C, rnd为(0,1)内均匀分布的随机数.
步骤3) 网络参数初始化. 包括最大步数G、 初始速率β0、 终止速率βf、 初始邻域半径r0、 终止邻域半径rf、 初始方差σ0、 终止方差σf和当前步数t=0.
步骤4) 按下式计算当前速率、 邻域半径和方差:
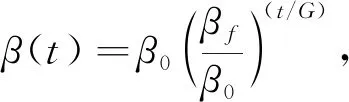
(11)
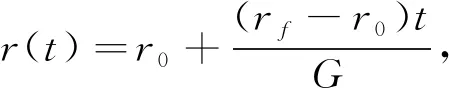
(12)
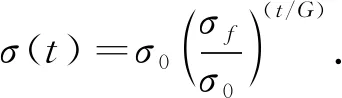
(13)
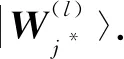
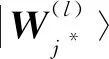
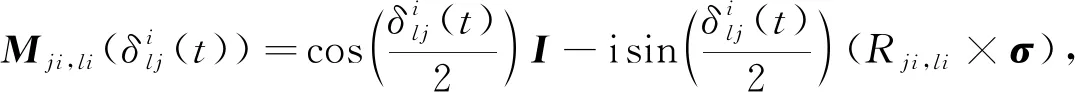
(14)

(15)

(16)
式中j∈ψ(j*,r(t)),i=1,2,…,n,l=1,2,…,L.
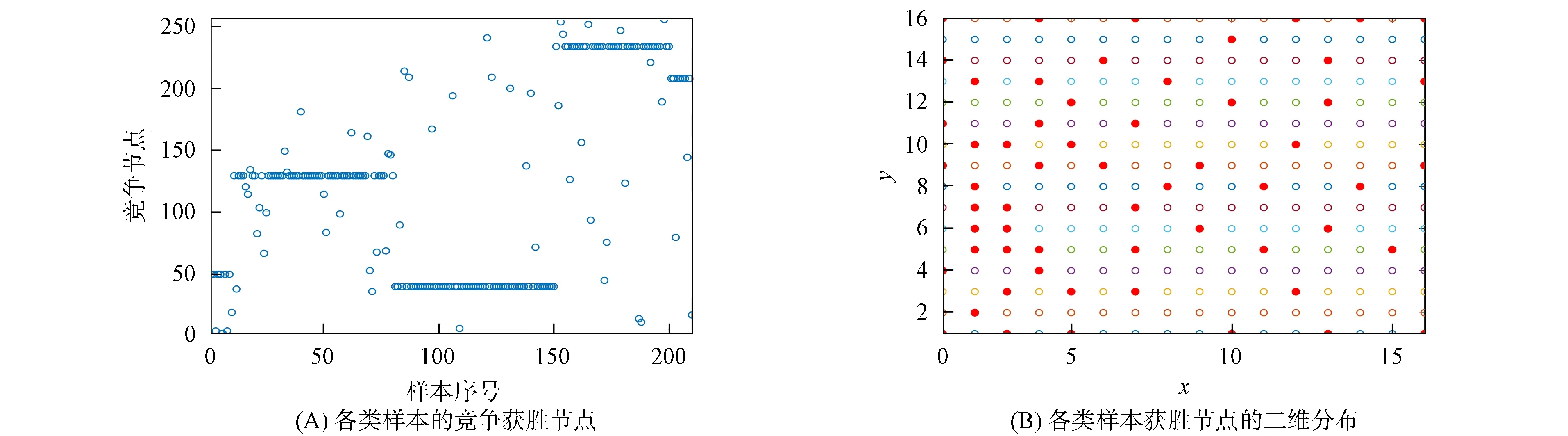
步骤7) 若t≥G或t 当油层被水淹后, 储层的物理性质将发生变化, 如电阻率、 自然电位、 声学性质及核物理性质等, 这些物理性质将反应在测井资料上, 根据水淹层作为注水或辺底水驱油油藏油层分级评价标准, 对水淹的级别进行划分. 以辽河油田某区块为例, 水淹级别可划分为未水淹、 弱水淹、 中水淹、 强水淹和特强水淹5种, 这5种水淹级别可作为模型的水淹级别集合, 该集合中每个元素将作为训练样本的类别标签. 由于水淹导致储层的岩性、 物性和含油特征等发生变化, 因此在构造水淹层识别特征指标集时要充分考虑这些因素. 构造方法: 为寻求水淹层测井响应特征与水淹层级别之间的映射关系, 根据专家对密闭取心井已有取心资料的解释分析并进行综合测试, 从而选取对水淹层识别反应好的测井资料响应特征构造特征指标参数样本. 以辽河油田某区块为例, 通过综合测试和分析对比, 确定自然电位(SP)、 自然伽马(GR)、 声波时差(AC)、 微梯度(RML)、 深侧向电阻率(RT)、 浅侧向电阻率(RS)、 微电位(RMN)、 孔隙度、 含油饱和度作为水淹层特征指标参数. 对每个储层, 前7个特征为测井曲线数据, 后2个特征为单个数值. 原始测井曲线数据存在的噪声(主要表现为异常高的突变值), 会影响聚类及识别效果, 所以需要执行滤波处理. 本文采用经典的Walsh滤波方法. 该方法的原理: 首先对测井曲线进行离散Walsh变换, 忽略某些高频分量后, 再执行反变换重构原曲线. 该过程的本质是对原始曲线执行“削尖”和“平滑”处理. 令离散数据序列的长度L=2P, 若不满足可在后面补零, 离散Walsh变换可表示为 (17) 离散Walsh滤波即为在采用W(k)合成x(n)时, 只采用前2P-M个W(k), 表示为 (18) 此时合成的x(n)即可达到“削尖”和“平滑”的目的. 每个储层采用9个特征描述, 其中前7个特征均来自测井曲线的离散数据序列, 对这些序列实施离散Walsh滤波后, 取这些序列的均值, 可得7个特征值, 再与孔隙度及含油饱和度合在一起, 即可得到描述单个储层样本的9维特征向量. 由于不同特征的数量级不同, 为消除不同量级数据间的相互影响, 还需对所有样本逐维进行归一化处理. 为验证QSON的有效性, 将本文方法与传统自组织网络(classical self-organization network, CSON)[22]、K-均值聚类(K-mean)[23]、 最邻近聚类(nearest neighbor clustering, NNC)[24]3种算法进行对比. 为使对比结果更客观公正, 对于CSON, 本文采用与QSON相同的结构和参数. 设置QSON和CSON模型的参数: 输入节点个数等于储层特征参数个数(9个), 竞争层节点C=256, 且排成16×16方阵; 最大步数G=1 000. 经过多次实验, 本文最终确定最佳参数组合为: 初始速率β0=0.8, 终止速率βf=0.1, 初始半径r0=8, 终止半径rf=1, 初始方差σ0=8, 终止方差σf=0.5. 对于K-mean算法, 指定类数K=5, 聚类精度ε=10-5, 若连续两代所有类中心变化量均小于ε则算法终止. 对于NNC算法, 经过多次实验, 最终确定最佳聚类阈值为λ=0.9, 若某样本与某类中心的欧氏距离小于λ, 则视为该样本属于该类. 将预处理后的水淹层数据提交上述4种模型训练, 收敛后的模型即可用于水淹级别自动分类. 仿真实验采用MATLAB工具, 编程实现QSON算法, 对辽河油田某区块23口井共258个储层进行水淹级别聚类仿真, 其中超强水淹15个、 强水淹89个、 中水淹83个、 弱水淹59个、 未水淹12个. 这些小层的测井曲线共包含35 424个离散数据点, 数据点的空间分布形态如图2所示. 图2 258个储层的7条测井曲线 根据油藏开发实际情形划分小层的水淹级别共为5种类型: 特强水淹(编码为0)、 强水淹(编码为1)、 中水淹(编码为2)、 弱水淹(编码为3)、 未水淹(编码为4). 该区块某井部分原始样本数据列于表1. 该井共有7个小层, 其中第2~8列为测井曲线数据, 第9,10两列为单个数值. 为简便, 表1中每个小层分3行显示, 第一行和第三行分别表示该小层各测井曲线的顶深和底深数据, 第二行用省略号表示该小层的其他数据. 对所有258个小层的7条测井曲线分别执行Walsh滤波, 去除部分高列率成分后, 再反变换回原曲线. 先将每小层滤波后的数据取均值, 即可构造储层样本, 再将所有样本按维归一化即可得到训练样本, 归一化方法为: 首先获取所有样本每维的绝对值最大值, 然后将各维数据除以相应维最大值即可. 以表1中原始数据为例, 7个小层的归一化结果列于表2. 表1 辽河油田某区块某井水淹层部分原始特征数据 表2 辽河油田某区块某井水淹层聚类样本数据 首先将258个储层分为训练样本和测试样本, 其中训练样本210个(超强水淹10个、 强水淹70个、 中水淹70个、 弱水淹50个、 未水淹10个), 测试样本48个(超强水淹5个、 强水淹19个、 中水淹13个、 弱水淹9个、 未水淹2个); 然后将训练样本提交网络. QSON和CSON的训练结果分别如图3和图4所示. 由图3(A)可见, 仅经过310步迭代, 所有训练样本即聚为5类, 各类样本的获胜节点分别为: 节点28, 弱水淹; 节点55, 超强水淹; 节点76, 强水淹; 节点90, 未水淹; 节点170, 中水淹. 而且各类之间没有交叉误判, 聚类结果完全正确. 由图3(B)可见, 5个获胜节点的空间分布为: 弱水淹(2,12), 超强水淹(4,7), 强水淹(5,12), 未水淹(6,10), 中水淹(11,10), 这些节点在空间分布上相对分散, 可使网络有较强的泛化能力. 由图4(A)可见, 经过1 000步迭代后, 网络未收敛, 所有训练样本聚为59类, 其中: 第2,27,50类均有2个储层; 第10类有58个储层, 属于中水淹, 获胜节点序号为39; 第12类有6个储层, 属于超强水淹, 获胜节点序号为49; 第31类有48个储层, 属于强水淹, 获胜节点序号为129; 第49类有7个储层, 属于未水淹, 获胜节点序号为208; 第53类有34个储层, 属于弱水淹, 获胜节点序号为234; 其他51类均只有1个储层. 由图4(B)可见, 5个大类获胜节点的空间分布为: 第10类中水淹(3,7), 第12类超强水淹(4,1), 第31类强水淹(9,1), 第49类未水淹(13,16), 第53类弱水淹(15,10). 尽管这5个节点在空间分布上分散度较好, 但其他54类对应的54个点形成了类似噪声的干扰项, 从而在一定程度上影响了网络的泛化能力. 图3 QSON的训练结果 图4 CSON的训练结果 图5 K-mean和CNN的聚类结果 对于K-mean和NNC方法, 聚类结果如图5所示. 由图5可见: 对于K-mean聚类结果, 5类样本数分别为14(超强水淹), 72(强水淹), 48(中水淹), 40(弱水淹), 36(未水淹); 对于48个测试样本, 通过计算每个测试样本与各类中心的距离, 确定该测试样本的水淹级别, 正确识别数仅为15个, 正确识别率为31.25%; 对于NNC聚类结果, 5类样本数分别为121(超强水淹), 24(强水淹), 37(中水淹), 13(弱水淹), 15(未水淹); 对于48个测试样本, 正确识别数仅为14个, 正确识别率为29.166 7%. 由实验结果可见: QSON对测试集识别的正确率高于CSON, 尤其明显高于K-mean和NNC. 这主要因为: 首先, 在QSON中采用了新的距离度量方式. 现有的各种聚类算法大都采用基于两点各维坐标的欧氏距离; 而在QSON中, 采用Bloch坐标计算两点之间的球面距离. 从而使得QSON比其他3种对比算法对待识别样本具有更好的区分能力, 使其具有更优良的聚类性能; 其次, QSON采用量子比特绕轴旋转调整权值, 调整过程在三维Bloch球面上进行, 从而使调整过程更精细; CSON直接采用样本和权值的向量差调整权值, 该方法对学习速率较敏感, 但调整过程不易控制. 此外, 由于引入较多的矩阵计算(投影测量、 绕轴旋转等), 导致QSON的计算效率较低, 但正是由于增加了这些辅助操作, 才有效提高了QSON的聚类能力. 综上所述, 为解决油田测井解释中的水淹层识别问题, 本文提出了一种基于量子自组织网络的水淹层识别方法. 该方法输入和权值均采用量子比特描述, 权值调整采用量子比特在Bloch球面上的绕轴旋转实现. 实验结果表明, 该方法聚类能力不仅高于传统自组织网络, 而且大幅度高于K-均值聚类和最邻近聚类方法. 但由于采用了较多的矩阵计算, 导致本文方法计算效率较低.2 水淹层特征参数的选择
2.1 划分水淹级别
2.2 构造水淹层特征指标集
3 基于QSON的水淹层识别
3.1 原始数据的滤波去噪
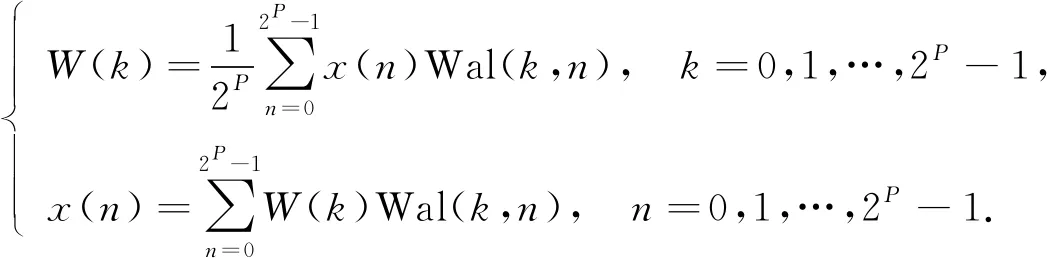
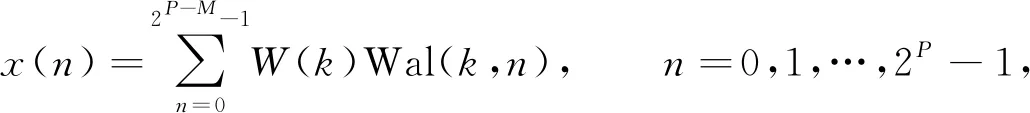
3.2 构造样本数据
3.3 基于QSON的水淹层聚类
4 实际应用
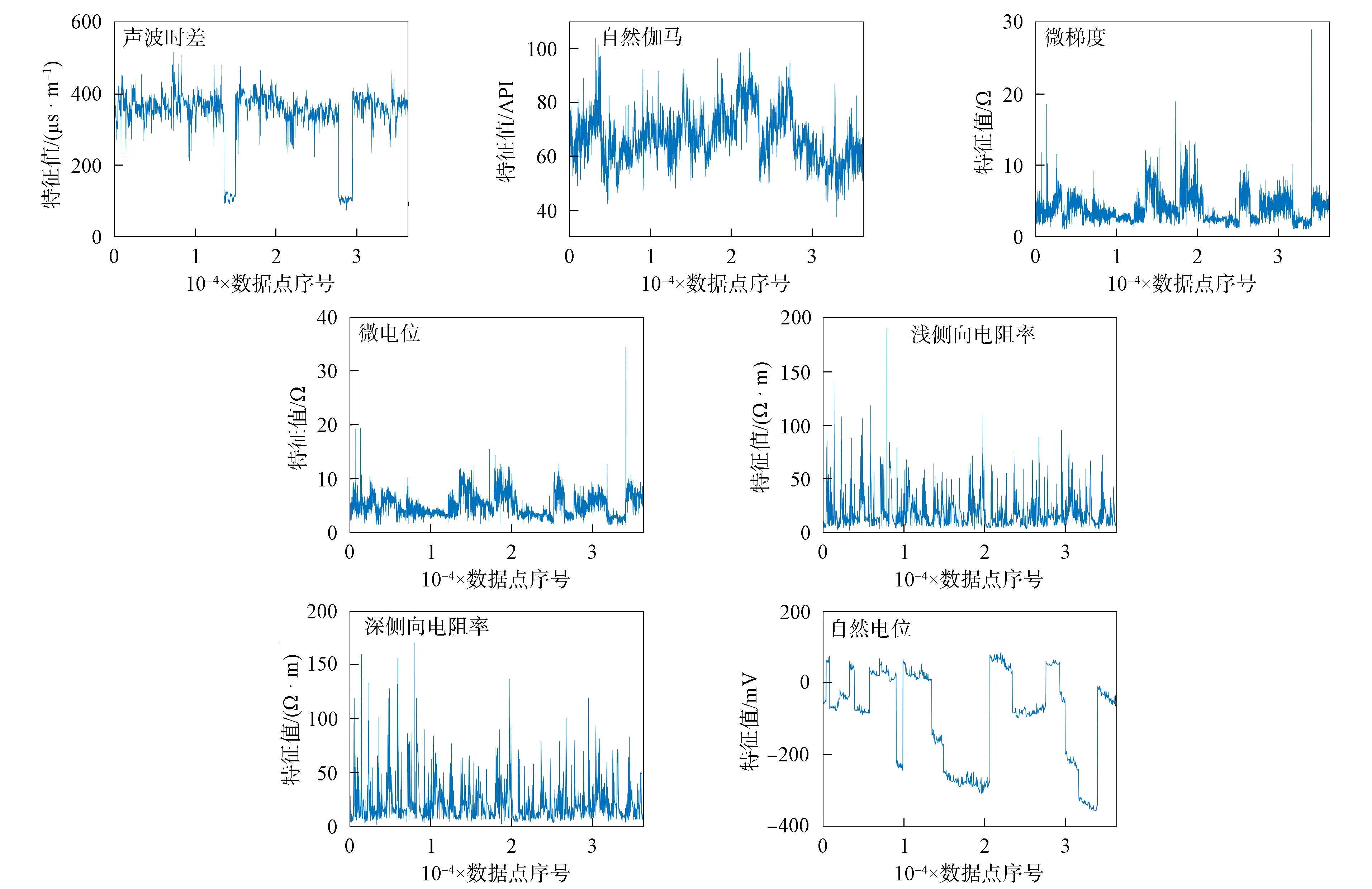
4.1 数据预处理
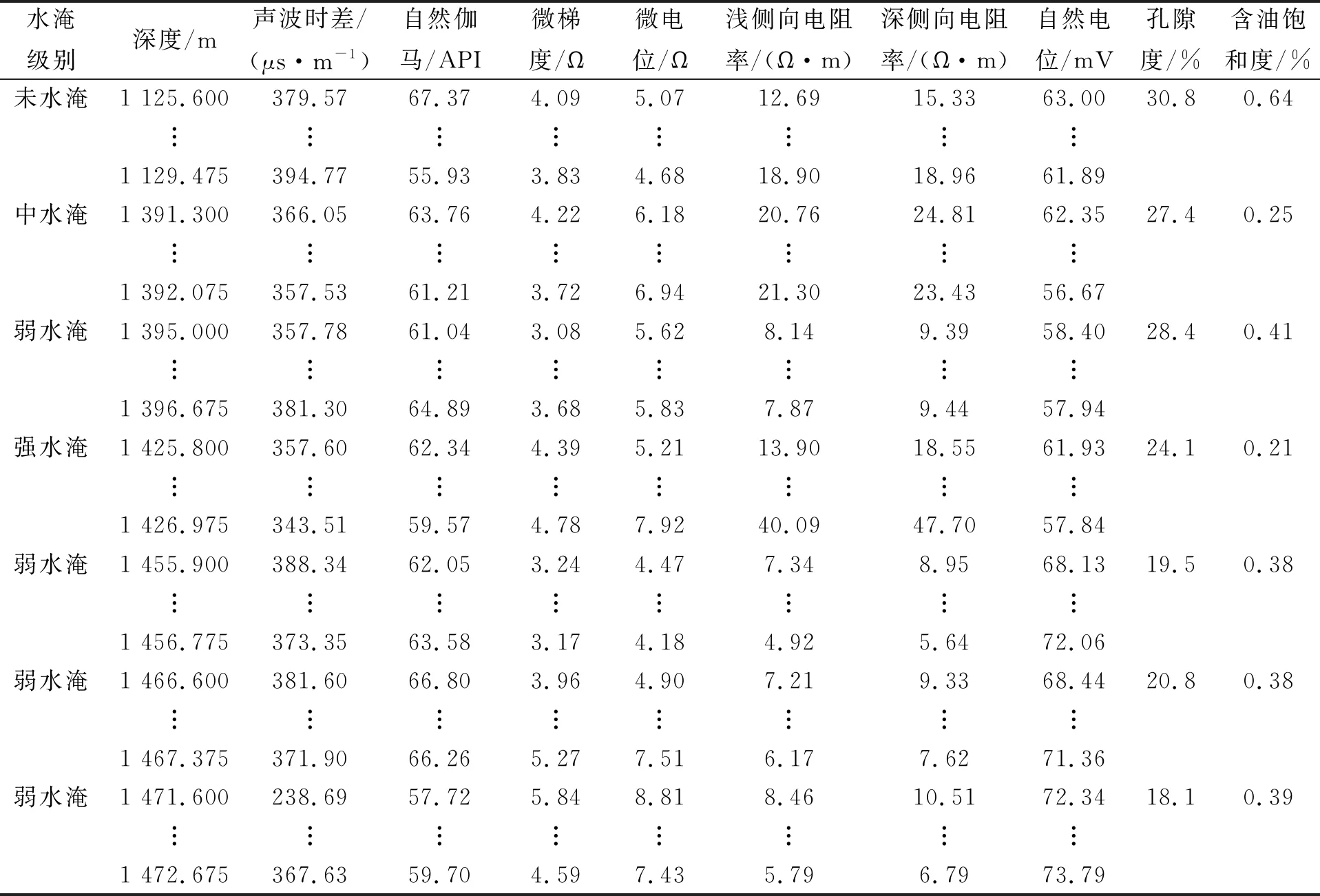
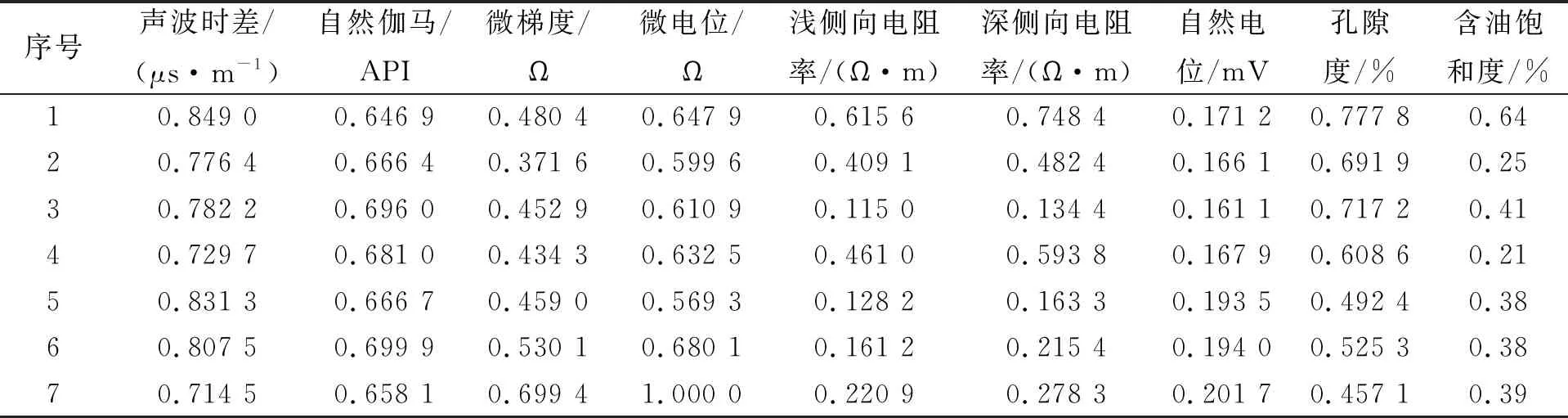
4.2 训练结果对比
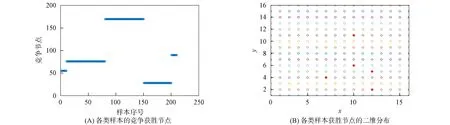
4.3 测试结果对比

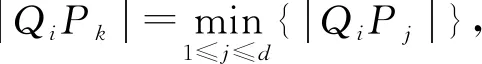
4.4 实验结果分析
