基于跨层复制连接卷积神经网络的遥感图像融合
2020-07-18王明丽郭晓新王献昌
王明丽, 王 刚, 郭晓新, 王献昌
(吉林大学 计算机科学与技术学院, 长春 130012)
遥感图像广泛应用于军事侦察、 变化检测和水质监测[1]等领域. 由于遥感卫星传感器自身的限制, 因此不能同时获得具有高空间分辨率和高光谱分辨率的图像[2]. 在实际应用中, 如植被识别、 地图更新和岩性分析等领域, 需要同时使用高空间分辨率信息描述图像的纹理和高光谱分辨率信息判断图像的类别[3]. 遥感图像融合通过将具有高空间分辨率、 低光谱分辨率的全色图像(panchromatic image, PAN)中的空间信息与具有低空间分辨率、 高光谱分辨率的多光谱图像(multispectral image, MS)中的高光谱信息融合, 获得同时具有高空间分辨率和高光谱分辨率的融合图像.
目前, 图像融合方法分为3个处理级别: 像素级、 特征级和决策级[4], 其中像素级融合方法应用广泛. 像素级的融合方法逐像素对图像进行处理, 处理精度高, 产生的融合图像能获得比特征级和决策级所处理的图像更丰富的纹理. 传统遥感图像像素级融合方法主要分为两类: 基于成分替代(component substitution, CS)的方法和基于多尺度分析(multiresolution analysis, MRA)的方法. 成分替代法有强度色度饱和度(intensity-hue-saturation, IHS)变换[5]、 比值变换(brovey transform, BT)[6]和主成成分分析(principle component analysis, PCA)[7], 通过将MS图像转换到某种空间域中, 并用PAN图像替换在该空间域中与PAN图像相关性最高的分量, 最后经空间域逆变换得到融合图像. 该方法能有效地将PAN图像的空间信息注入MS图像中, 但当PAN图像与被替换的分量局部差异较大时, 光谱扭曲问题严重[8]. 基于多尺度分析方法有小波变换(wavelet transform, WT)[9]、 高通滤波器(high pass filter, HPF)[10]和非向下采样轮廓波变换(non-subsampled contourlet transform, NSCT)[11]等, 该类方法首先对多源图像进行多尺度分解, 再在不同尺度上根据各分量的特点选择不同的融合规则, 最后经分解逆变换得到融合图像. 图像的分解方法、 分解层次和在不同级别中选择的融合规则将对最终的融合结果产生较大影响. 传统遥感图像方法都是在对图像处理过程理解的基础上人工选择融合规则进行融合, 不能妥善处理由于环境变化或不同类型数据带来的影响, 普适性较低.
卷积神经网络(convolutional neural network, CNN)[12-16]由于其具有权值共享和局部连接等特性, 使其与传统方法相比有更好的鲁棒性和容错能力, 并且能更好地保留图像的纹理信息, 已广泛应用于图像分割、 计算机视觉识别和图像分类等领域. 全卷积网络(fully convolutional networks, FCN)是一种用于图像语义分割的网络, 其对图像进行像素级的分类, 从而解决了语义级别的图像分割(semantic segmentation)问题. U-Net是一种基于全卷积网络, 已成功应用于医学图像分割的网络结构[17]. U-Net在全卷积网络基础上去掉全连接层, 由于医学图像分割需对每个像素点进行精准分类, 所以U-Net将来自网络收缩路径的高分辨率特征与网络上采样输出相结合进行处理, 通过跨层复制连接操作将信息组合后学习, 可得到更精确的分类结果.
本文提出一种基于跨层复制连接卷积神经网络的端到端遥感图像融合模型, 克服了传统融合方法需人工制定融合规则, 且模型易实现. 首先, 构建输入是MS图像和PAN图像, 输出为融合图像的高效网络模型; 其次, 使用从公开数据库下载的遥感图像数据集构建训练集, 并利用构建好的训练集训练网络模型; 最后, 将MS图像上采样到PAN图像大小作为网络输入, 得到同时具有高光谱分辨率和高空间分辨率的融合图像. 实验结果表明, 与传统遥感图像融合方法相比, 本文方法有更好的鲁棒性, 能有效抑制光谱扭曲并提升融合图像的质量.
1 基于卷积神经网络的图像融合
1.1 FCNNs模型
本文提出的基于跨层复制连接卷积神经网络的遥感图像融合模型----FCNNs, 融合方法包括以下3个步骤:
1) 构建训练集;
2) 使用训练集训练FCNNs模型;
3) 选择MS图像的R,G,B波段作为待融合的MS图像, 将MS图像上采样为PAN图像分辨率, 并使用FCNNs模型融合上采样的MS图像和PAN图像, 得到具有更好空间细节和光谱特征的融合图像.
用具有3个分支的卷积神经网络建立回归模型, 训练好的网络等价于传统遥感图像融合中的融合规则. 卷积神经网络包含的卷积层越多, 所提取的特征图对应原始图像中越大的区域, 可将其视为一种特殊的多尺度分解方法. 这种较大的特征图可提供更好的图像解译能力. 卷积运算用于计算融合图像, 其不仅考虑了待融合图像中的像素点, 也考虑了其周围像素点.
为了更好地保留PAN图像的空间信息和MS图像的光谱信息, 删除了传统卷积网络中的下采样层[18]. FCNNs模型结构如图1所示, 其等价于融合规则FCNNs(MS,PAN)=fusion. FCNNs包含3个分支: 上下分支M和P分别表示对MS图像和PAN图像的特征提取; 中间主分支MP进行融合操作.
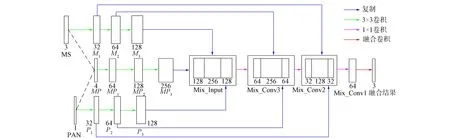
图1 FCNNs模型
M分支的操作可表示为
M1=F(WM1*MS+BM1),
(1)
其中: MS为输入的三通道多光谱图像; *表示卷积运算;WM1表示尺寸为3×N×N×nM1的卷积核;BM1表示M1层的偏置向量;nM1为卷积核的个数. 同理可得:
M2=F(WM2*M1+BM2),
(2)
M3=F(WM3*M2+BM3).
(3)
P分支的操作可表示为
P1=F(WP1*PAN+BP1),
(4)
其中: PAN为输入的单通道全色图像;WP1表示尺寸为1×N×N×nP1的卷积核,nP1为卷积核的个数;BP1为偏置向量. 同理可得:
P2=F(WP2*P1+BP2),
(5)
P3=F(WP3*P2+BP3).
(6)
MP分支的前三层卷积层将MS图像和PAN图像同时作为输入进行卷积, 可表示为
MP1=F(WMP1*MP+BMP1),
(7)
其中:MP为将MS图像和PAN图像连接作为输入的四通道图像;WMP1表示尺寸为4×N×N×nMP1的卷积核,nMP1为卷积核的个数;BMP1为偏置向量. 利用前三层的计算结果继续进行卷积运算可得:
MP2=F(WMP2*MP1+BMP2),
(8)
MP3=F(WMP2*MP2+BMP3).
(9)
与传统CNN网络相比, FCNNs模型增加了跨卷积层的复制连接操作, 将高层分辨率信息通过跨层复制连接操作传播到混合层进行融合, 能更好利用多源图像的局部信息, 并弥补在卷积过程中的信息损失. 多源图像经不同层卷积网络得到的多尺度特征图, 在混合卷积层进一步融合, 能得到更高质量的融合图像.MP分支中的混合卷积层可表示为
与传统遥感图像融合人为设计滤波器不同, FCNNs模型的卷积核是基于大量的遥感图像数据训练获得的. 由于纯卷积运算是线性的, 因此FCNNs模型在每个卷积层后还增加了非线性激活运算, 以增强模型的融合能力. FCNNs模型的融合过程表示为
F=ReLU(W,X),
(13)
ReLU(x)=max{0,x},
(14)
其中:W为卷积核;X为输入; ReLU为非线性激活函数;x表示ReLU的输入.
在混合卷积层后利用多个滤波器数量逐渐递减的1×1卷积核将得到的Mix_Conv1特征图转化为三通道, 得到融合结果为
Fusion=F(Wfusion*Mix_Conv1+Bfusion).
(15)
1.2 构建训练集
本文使用大量遥感图像数据构建卷积神经网络模型, 建立多源遥感图像像素点与融合图像像素点之间的回归关系. 训练后的回归模型可生成具有更好空间细节和光谱特征的高分辨率多光谱融合图像. 为了成功地训练回归模型, 首先需构建合适的训练数据集.
在实际应用中不存在理想的融合图像, 即没有用于训练FCNNs模型的目标融合图像. 所以为了训练回归模型, 需将MS图像和PAN图像下采样到低分辨率水平. 根据Wald协议[19], 可将下采样的遥感图像视为在对应较低分辨率水平传感器获得的遥感图像. 因此, 将PAN图像下采样到MS图像大小, 得到的低分辨率PAN图像记为PAN_L, 将MS图像先下采样到1/2尺寸, 再将其上采样到原始图像大小, 得到的低分辨率MS图像记为MS_L. MS_L和PAN_L作为样本输入到回归模型中, 同时将原始MS图像作为模型的训练目标, 训练集可表示为
Dataset={[MS_L,PAN_L],MS}.
(16)
本文使用的遥感图像来自Landsat 8卫星. Landsat 8卫星图像中的4,3,2波段对应于MS图像的R,G,B波段, 分辨率为30 m, 8波段对应于PAN图像, 分辨率为15 m. 训练好的FCNNs模型可直接处理大尺寸的遥感图像, 但基于计算效率考虑, 参与训练图像的大小通常比原始图像小得多. 本文使用的训练数据集包含10万个训练样本, 大小为64×64. 图2为训练样本示例, 其中: (A)为融合目标, 即原始MS图像; (B)为MS_L图像; (C)为PAN_L图像.

图2 训练集示例
1.3 训练集的训练及参数设置
本文的核心是利用构建好的训练集Dataset训练回归模型FCNNs. 记FCNNs模型的参数为θ, 则模型的训练过程可表示为
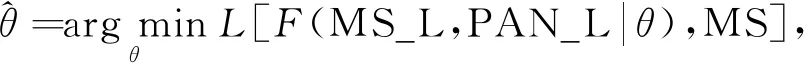
(17)
其中:F表示融合模型FCNNs;L表示基于回归模型输出和目标输出之间误差定义的损失函数. 采用均方误差损失函数作为优化目标, 定义为
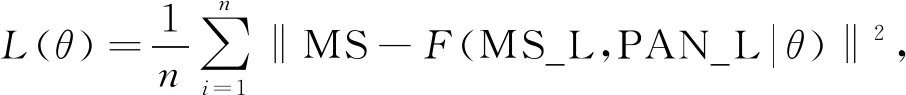
(18)
其中n为训练集中样本的数量.
基于平衡融合质量和计算资源的考虑, 本文将使用的卷积核N设为3, 因为3×3的卷积核是能最小捕获上下、 左右和中心域信息的尺寸, 步幅设为1. 在混合卷积层和最后的融合层, 使用多个1×1卷积核. FCNNs每层卷积核的数量列于表1.

表1 FCNNs模型各层卷积数量
在Nvidia GTX 2080Ti GPU上训练FCNNs模型, 并使用随机梯度下降法最小化损失函数. Adam算法是一种基于随机梯度下降的自适应学习优化方法, 计算效率较高. 因此, 本文选择Adam算法作为优化算法更新模型参数. 学习率初始设定为0.001, 训练迭代次数为10, 学习率在第四次和第八次分别进行学习率衰减. 训练数据集被分为小批量, 而每批包含64个样本. 全部训练时间为35 min, 训练完成的平均训练误差为0.001 4.
2 实验结果与分析
为验证本文算法的有效性, 将本文算法的实验结果与传统融合方法色彩超球面锐化变换(hypersphere color sharpening, HCS)、 小波变换(WT)、 比值变换(BT)、 高通滤波器融合(HPF)和主成分分析(PCA)进行比较. 所选取的图像来自Deimos卫星和QuickBird卫星数据集, 对比算法的参数设置与本文融合方法中所设置的参数相同. 通过主观感知和客观指标相结合的评价方法对本文遥感图像融合方法进行评价.
2.1 评价指标
为定量评估融合后遥感图像的质量, 选择均方根误差(root mean square error, RMSE)[20]、 相对全局综合误差(erreur relative globale adimensionnelle de synthese, ERGAS)[21]、 相关系数(correlation coefficient, CC)[22]、 相对平均光谱误差(relative average spectral error, RASE)[23]、 峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性(structural similarity, SSIM)[24]6个评价指标对融合图像进行评价. 由于不能获得理想的融合图像, 因此为了定量评价光谱信息, 本文使用原始MS图像作为参考图像, 将下采样得到相同大小的MS图像和PAN图像进行融合.
1) 均方根误差(RMSE)为
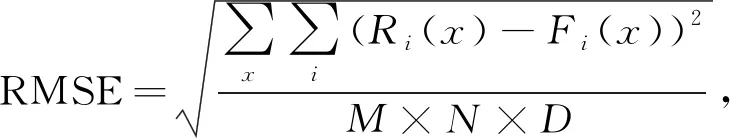
(19)
其中:R为参考图像;F为融合图像;M和N分别为图像的宽和高;D为图像的波段数. 式(19)用于计算融合图像与参考图像之间误差的标准值, 该值越接近0, 表示融合图像与参考图像越相似, 融合质量越高.
2) 相对全局综合误差(ERGAS)为
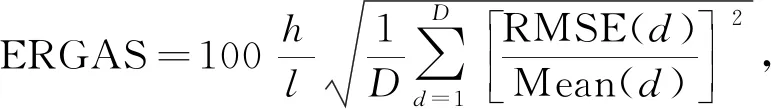
(20)
其中:h/l表示PAN图像与MS图像的分辨率比值; Mean(d)表示每个子带的平均值. 计算结果表示融合图像与参考图像各波段之间的误差, 其值越小, 融合效果越好.
3) 相关系数(CC)为
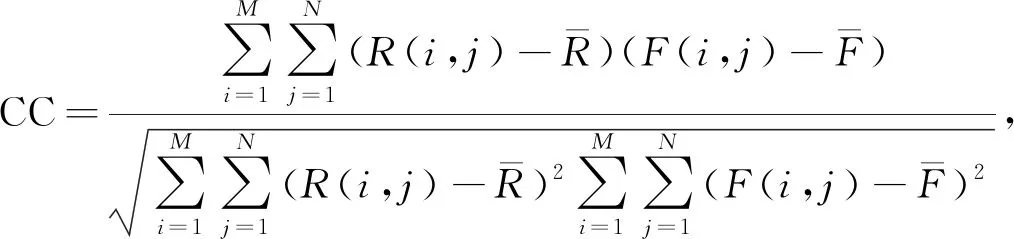
(21)
其中:R(i,j)和F(i,j)分别表示参考图像和融合图像在(i,j)处的像素值. 式(21)表示融合图像与参考图像之间光谱相似度, 该值越接近于1表示融合图像与参考图像越相似, 融合效果越好.
4) 相对平均光谱误差(RASE)为

(22)
其中: Mean(R)表示参考图像的均值, 式(22)表示图像光谱细节信息损失, 该值越小, 融合图像质量越高.
5) 峰值信噪比(PSNR)为
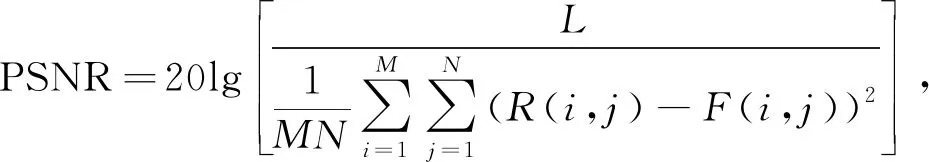
(23)
其中L表示融合图像的最大灰度值. 式(23)用于衡量有效信息和噪声的比率, 该值越大表明融合图像与原始图像之间失真越小, 融合图像质量越好.
6) 结构相似性(SSIM)为
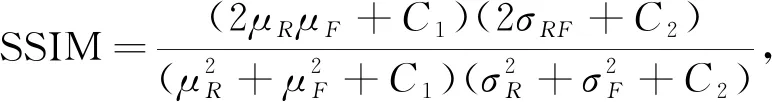
(24)
其中:μR,σR,μF,σF分别表示参考图像和融合图像的灰度均值和标准差;σRF表示参考图像和融合图像之间的灰度协方差. SSIM取值范围为[-1,1], 该值越接近1, 表示融合图像与参考图像之间的结构、 亮度、 对比度越相似, 融合质量越好.
2.2 结果分析
本文使用4组实验验证算法的有效性, 前两组实验图像来自Deimos卫星, 后两组实验图像来自QuickBird卫星. 使用MS图像的R,G,B波段和PAN图像进行融合. 4组实验MS图像大小为200×200, PAN图像大小为800×800. 为了客观评价融合图像的质量, 本文将原始MS图像作为参考图像, 将重采样的MS和下采样的PAN图像作为输入进行融合. 4组实验图像融合结果分别如图3~图6及表2~表5所示.
由图3可见: HCS,BT和PCA算法虽然可有效地将PAN图像的空间信息保留, 但有严重的光谱扭曲; WT算法很好地保留了MS图像的光谱信息, 但在空间纹理细节上存在光谱失真; HPF算法将PAN图像不具有的空间信息加入, 导致融合图像人工痕迹明显. 由图4可见: PCA算法得到的融合图像偏暗; HCS和BT算法虽然很好地保留了光谱信息, 但融合后的结果相比于本文算法在空间细节上较差; WT算法局部空间细节出现光谱失真; HPF算法虽然空间纹理信息保持较好, 但融合图像颜色饱和度不够, 有一定的光谱扭曲. 由图5和图6可见: HCS,BT和PCA算法都存在不同程度的光谱扭曲; WT算法空间失真较严重; HPF算法将图像的空间纹理信息加强, 但光谱信息保存不足.

图3 第一组Deimos卫星测试图像及融合结果
由表2~表5可见, 本文模型FCNNs得到的融合图像的各项指标均优于对比传统融合算法, 表明本文算法在光谱信息保存完整的情况下, 融合图像的空间细节信息得到有效提升. 本文算法在不同的卫星上通过主观感知和客观评价都优于对比算法, 成功验证了本文遥感图像融合模型FCNNs有更好的适应性, 且在保留MS光谱信息的同时能有效提升融合图像的空间分辨率.

图4 第二组Deimos卫星测试图像及融合结果
综上所述, 本文提出了一种基于跨层复制连接卷积神经网络模型FCNNs的遥感图像融合算法. 该算法克服了传统遥感图像算法基于人工制定遥感图像融合规则, 不能妥善处理由于环境变化或不同类型卫星数据带来的影响. 本文模型中的各层卷积核通过大量遥感图像数据训练得到, 对不同类型遥感图像适应性较好. 为更好地保留多源遥感图像中的信息, 取消了传统神经网络的下采样层, 并通过跨层复制连接操作构建了一个更适合于遥感图像融合的卷积神经网络模型. 通过跨层复制连接网络结构, 更好地利用了多源图像的局部信息, 并将不同尺度的特征图在混合卷积层进行处理, 提供了对多源遥感图像的多尺度融合. 通过主观感知和客观评价将本文算法与其他传统融合算法进行对比, 验证了本文算法能更好地保留MS图像的光谱信息, 并有效提升融合图像的空间细节信息, 抑制光谱扭曲.

图5 第三组QuickBird卫星测试图像及融合结果

图6 第四组QuickBird卫星测试图像及融合结果

表2 第一组Deimos卫星融合图像客观评价结果
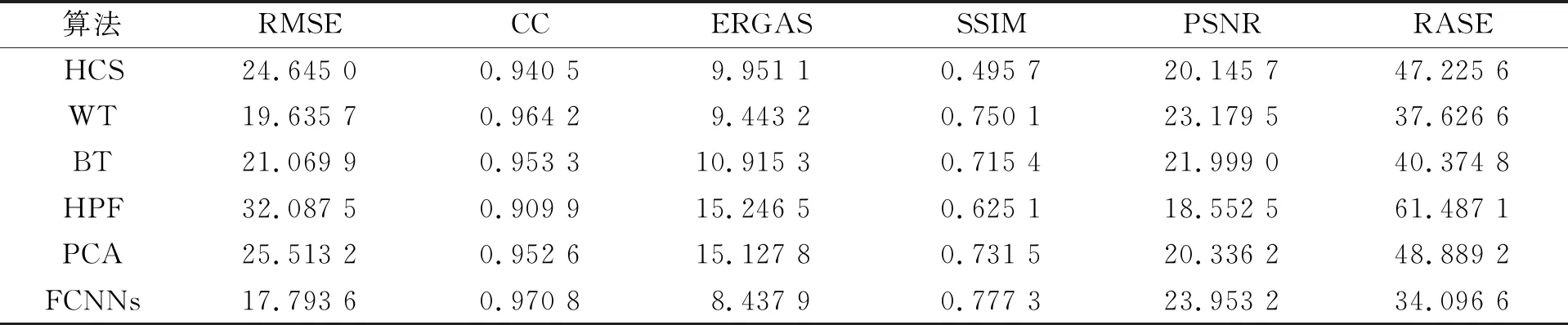
表3 第二组Deimos卫星融合图像客观评价结果
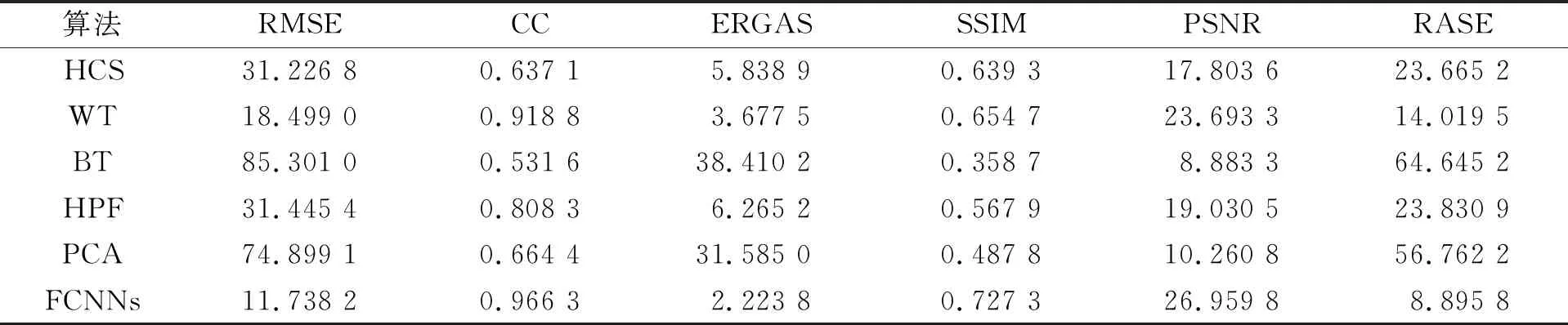
表4 第三组QuickBird卫星融合图像客观评价结果
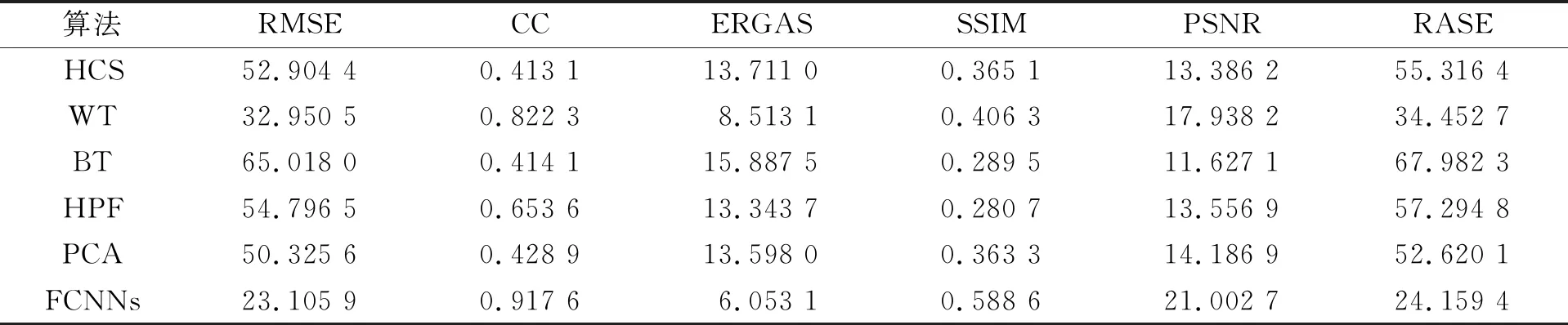
表5 第四组QuickBird卫星融合图像客观评价结果
