结构化方法下CDS 保费和价格的计算
2020-07-18周梦晨姜瀚成马越纪尚明峰曹雅婷高雨倩苏州大学
周梦晨 姜瀚成 马越纪 尚明峰 曹雅婷 高雨倩 苏州大学
本文在结构化方向下建立CDS 定价模型,在结构化方法的框架下,违约对于公司资产来说是一个可观测事件。相较于传统的结构化模型,本章对于标的债券公司的违约边界构造了一个更客观、符合中国债券市场实情的判定方法,公司价值必须低于界限值并维持一段时间才会判定违约。
在本文中,标的债券公司的股票满足Black-Scholes 公式,且符合几何布朗运动,在首次到达时间模型中,通过对过程进行数值采取蒙特卡洛模拟的方式刻画违约时间。这种方法把违约时间同公司资产联系起来,更具客观性,并能灵活地应用于中国债券市场。本章主要介绍了在结构化框架下对于违约时间的刻画以及利用结构化方法确定CDS保费率的数学模型。
一、保费率为k
考虑一份到期日为T的信用违约互换,其参考标的是面值L,到期日的可违约零息债券,该CDS 在债务违约时刻τ赔付。CDS 的具体执行过程是保护买方在到期日T或者违约前的规定时刻支付保费kL。
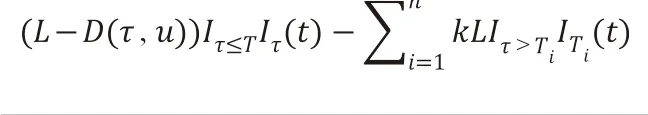
根据保护买方的贴现现金流在风险中性定价测度下期望为0 来构造等式移项后得到保费率k的计算公式[1]:

其中,ru为无风险利率,与时间u相关。
二、违约时间
结构化方法下,违约时间τ对于参考信息是可观测事件。在明确公司资产与违约边界的情况下,相较于约化方法能够提高违约时间τ的精度。本节通过公司资产St及其违约边界来刻画违约时间τ。
(一)首次到达时间模型
考虑标的债券为某公司发售的零息票债券,这张债券不向持有者支付息票,只在到期日向持有者支付债券面值L,设公司的资产过程St符合Black-Scholes 定价方程,且服从几何布朗运动:
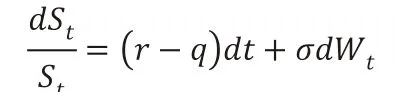
其中,r为资产流入率,q为资产流出率。σ为公司资产波动率,Wt为标准布朗运动,符合正态分布。

通过求解可以得到公司资产的变化过程:

对于公司资产波动率σ,我们可以用如下公式计算[2]:
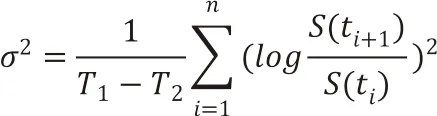
接下来,我们定义公司资产的违约界限过程b(t):
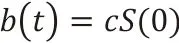
其中:c 为给定的界限值,我们选择c=0.8。下面我们定义违约时间τ,基于首次到达模型,违约发生在债券到期日前的任意时刻。因此,违约时间τ可有下面的公式进行描述:
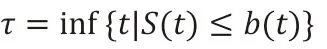
(见图1)
(二)到达-检验模型
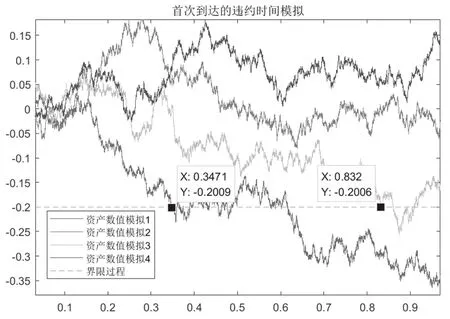
图1
实际情况中,金融市场会出现短时的剧烈震荡,导致短时数据的失真。例如:2020年的原油宝事件等。此时,公司价值会短暂低于界限,但是由于政府的政策支持等原因,这样的情况仅持续短时间,企业在一定的流动性支持下并不会发生大规模违约。为了使违约时间的刻画更接近实际的债券市场,我们认为:公司价值必须低于界限并维持一段时间才能判定违约。
新方法下和首次到达模型对于相同的一个资产变化可能会带来不同的结果,对比图如图2:
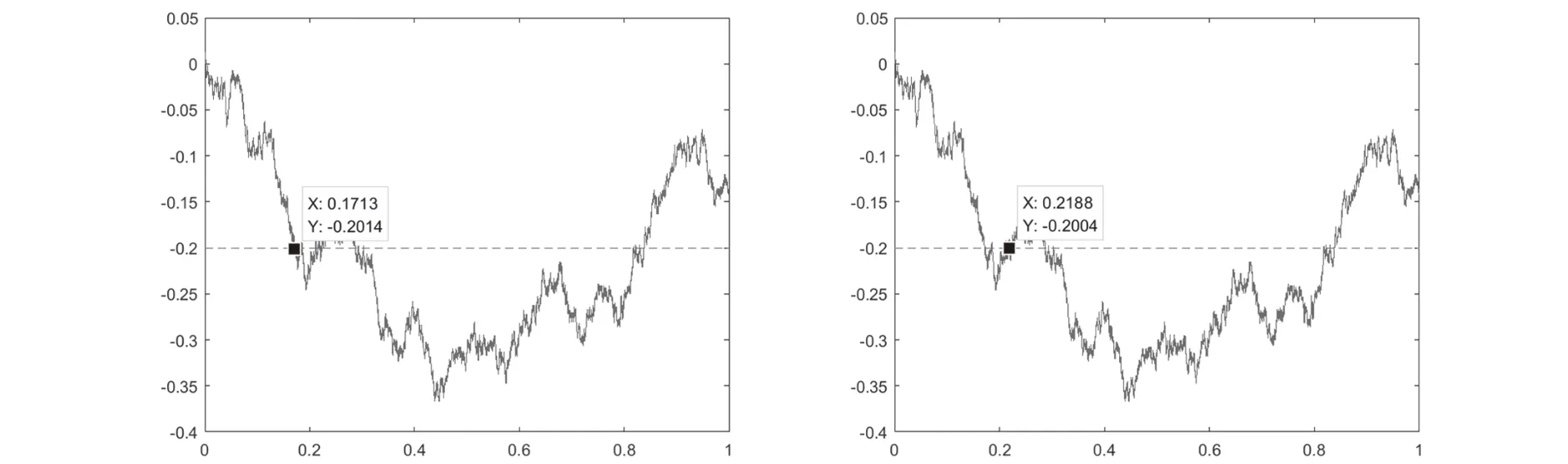
图2
连续过程的计算比较复杂,采用蒙特卡洛模拟后可以通过观察方法。但是,对于大量和复杂数据下的机器计算,观察并不能有效、准确得出结论,不同尺度的图片可能在视觉上会产生巨大变化,导致主观判断错误的情况。项目组采用离散化的思想给出编程的理论模型。
步骤一:选择违约集G中时刻的最小值作为t0;
步骤二:选取k=1,2,3…直到满足: 步骤三:步骤二中出现符合条件的t0,则其为在二分法下确定的最小违约时间,如果在步骤一中G已经被删为空集,则认为没有发生违约,。 该方法在使用概率论知识求解时只需要按照离散化的思想,保证后续的即可。即对于违约概率应该为上述检验点处违约概率的乘积,考虑到数值计算的精度,建议采用二分法或者等距选点检验的方法,否则数据计算误差会成为计算的主要误差。改进后的违约时间模拟如图3,在资产模拟2 中不再选取第一次到达的时间,在资产模拟1 中的短时间低于界限过程也不再判定为违约情况发生。 通过离散化时间的方式,我们可以发现并不是所有的违约发生的同时可以被发现,只有在部分条件处罚时才会吸引人们的注意力,公司会被发现违约。考虑如果违约时间τ在时间段发生,那么在时刻被发现,那么: 此时采用蒙特卡洛模拟的方法可以预测违约时间τ。但注意:该简化的方法不能运用在上市公司、大型知名企业的债券违约的分析上,主要是可以运用在付息的债券在付息日触发违约的情况。当时间段越来越稠密时结果收敛于连续假设下的违约时间,模型具备良好的稳定性和收敛性。 ·对于一张无对手信用风险的CDS 的购买者来说: ·在债券到期日T之前以保费率支付保费; 图3 ·当CDS 合约到期时,合约结束。 那么,这张CDS 的定价为: 对ut进行贴现,考虑为一个鞅,运用公式,利用dt项为0,可得ut满足的偏微分方程组: 这是一个一维热传导方程,可以采用Poisson 公式进行求解。在使用Poisson 公式前需要对方程组中的进行线性变换,使得模型变成标准的一维热传导方程。热传导方程通过傅里叶变换的方法进行求解,相关理论在姜礼尚、陈亚浙等编写的数学物理方程讲义[5]中已经详细论述,这里不做过多介绍。 总之,采用微分方程方法求解含有信用风险的金融衍生品的定价可以分为以下几个步骤:①现金流分析,写出信用衍生品的贴现现金流。②决定相关信息,对贴现现金流取条件期望作为该产品的价格。③对违约时间进行建模。④计算条件期望,采用概率论知识或转化为偏微分方程进行求解。(三)违约时间简化模型
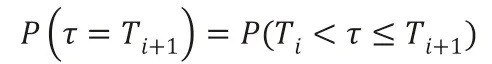
三、CDS 定价

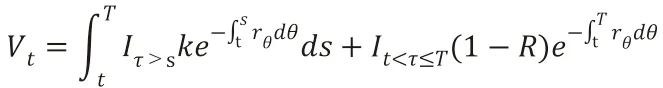
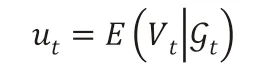
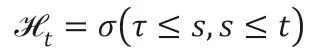
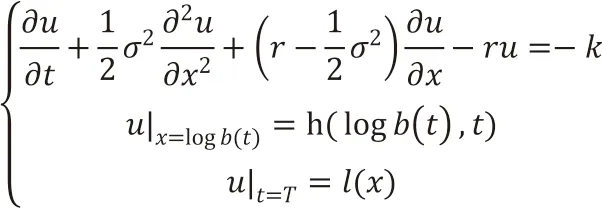
四、结语
